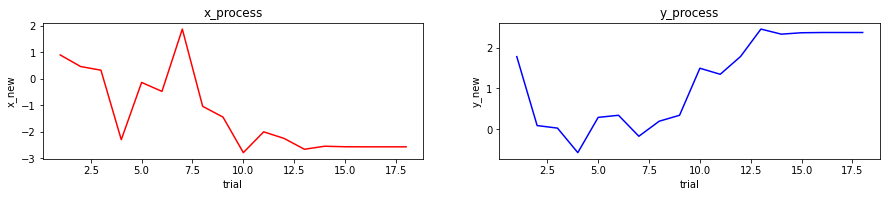
セカント法(1変数)
セカント法(2変数)
2変数のセカント法も作りました。
ブロイデン・フレッチャー・ゴールドファーブ・シャノン法(BFGS法)を使います。
$f(x, y)$ の最小解と最小値をセカント法で求める
\begin{aligned}
&\nabla f(x, y)=\left[\begin{array}{ll}
f_{x}(x, y) \\
f_{y}(x, y)
\end{array}\right] \\
&\left(\begin{array}{l}
x_{new} \\
y_{new}
\end{array}\right)=\left(\begin{array}{l}
x_{k+1} \\
y_{k+1}
\end{array}\right)-B_{k+1}^{-1} \nabla f(x_{k+1}, y_{k+1})
\end{aligned}
BFGS公式
B_{k+1}=B_{k}-\frac{B_{k} \boldsymbol{s}_{k} \boldsymbol{s}_{k}^{T} B_{k}}{\boldsymbol{s}_{k}^{T} B_{k} \boldsymbol{s}_{k}}+\frac{\boldsymbol{y}_{k} \boldsymbol{y}_{k}^{T}}{\boldsymbol{s}_{k}^{T} \boldsymbol{y}_{k}}
\boldsymbol{y}^{(k)}=\nabla f\left(\boldsymbol{x}^{(k+1)}\right)-\nabla f\left(\boldsymbol{x}^{(k)}\right)
\boldsymbol{s}^{(k)}=\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}
ニュートン法で $\nabla^{2} f(x_{old}, y_{old})$ というヘッセ行列を使ったところにヘッセ行列の近似行列 $B$ を用いる。
行列$B$の初期は単位行列が良いようなので、単位行列にしておきます。
1変数のセカント法の時も、初期値が2つ必要でしたが、
2変数の際も2つ必要になります。
$\boldsymbol{y}^{(k)}$ と $\boldsymbol{s}^{(k)}$ の部分を見れば分かると思います。
実装
ゴリ押しするのみです。
import matplotlib.pyplot as plt
import numpy as np
# 実装
def secant_method_2val(func0, func1, func2,
initial_x1, initial_y1,
initial_x2, initial_y2,
EPS):
"""
func0: f(x,y)
func1: f_x(x,y)
func2: f_y(x,y)
funcの部分はlambda関数で設定する。
func = lambda x,y : x+y+3
func(1,3) = 7
initial_x1,initial_y1 初期ベクトル1つ目
initial_x2,initial_y2 初期ベクトル2つ目
EPS:更新幅を止める基準
from BFGS Method.
"""
count = 0
# xの更新値の保存
x_new_list = [ ]
y_new_list = [ ]
diff = 10 # EPS基準で止めに行くが、止まらない値で設定しておく
B_ini = np.array([[0, 1,], [1, 0]]) # Bの初期値は単位行列にしておく
print("========== processing ==========")
while diff >= EPS:
count += 1
f_x1 = func1(initial_x1, initial_y1)
f_y1 = func2(initial_x1, initial_y1)
f_x2 = func1(initial_x2, initial_y2)
f_y2 = func2(initial_x2, initial_y2)
# 更新に必要なものを行列形式にまとめる
initial1 = np.array([[initial_x1], [initial_y1]]) # 初期値1を行列格納
initial2 = np.array([[initial_x2], [initial_y2]]) # 初期値2を行列格納
nabla1 = np.array([[f_x1], [f_y1]]) # 初期値1によるnabla(x,y)
nabla2 = np.array([[f_x2], [f_y2]]) # 初期値2によるnabla(x,y)
# 初期値の差分の行列, s_kにあたる部分
ini_diff = initial2 - initial1
ini_diff_T = ini_diff.T
# nabla(x,y)の差分の行列, y_k にあたる部分
nab_diff = nabla2 - nabla1
nab_diff_T = nab_diff.T
# BFGSの更新で必要なところを求めていく
# 第一項の分子
cal1 = np.dot(B_ini,ini_diff)
cal2 = np.dot(cal1,ini_diff.T)
cal3 = np.dot(cal2,B_ini)
# 第一項の分母
cal4 = np.dot(ini_diff_T,B_ini)
cal5 = np.dot(cal4,ini_diff)
# 第二項の分子
cal6 = np.dot(nab_diff,nab_diff_T)
# 第二項目の分母
cal7 = np.dot(ini_diff_T,nab_diff)
# BFGSでBを更新
B_new = B_ini - cal3/cal5 + cal6/cal7
B_new_inv = np.linalg.inv(B_new)
# 解の更新値を求める
new = initial2 - np.dot(B_new_inv, nabla2)
# count と 更新値
print("{}回目:x_new = {},y_new={}".format(count,new[0,0],new[1,0]))
x_new_list.append(new[0,0]) # xの更新値をリストに追加
y_new_list.append(new[1,0]) # yの更新値をリストに追加
# 更新幅
diff_x = abs(initial_x2 - new[0,0])
diff_y = abs(initial_y2 - new[1,0])
# diffの大きい方でwhileを止める基準にしたい
diff = max(diff_x,diff_y)
# 値の更新
initial_x1 = initial_x2
initial_y1 = initial_y2
initial_x2 = new[0,0]
initial_y2 = new[1,0]
B_ini = B_new
if count == 100: # 100回で収束しなければ
diff = 0 # diffを強制的に0にして
print("========== Do not CONVERSION =========") # while 文から抜ける
print("========== Result ==========")
print("solution:x = {}".format(new[0,0]))
print("solution:y = {}".format(new[1,0]))
value = func0(new[0,0],new[1,0]) # 解を代入した値
print("min_value:{}".format(value))
# グラフ描画
trial = np.arange(1, count+1, 1) # 1 ~ n回
fig = plt.figure(figsize=(15, 2.5))
ax = fig.add_subplot(1, 2, 1)
x_value = np.array(x_new_list)
plt.plot(trial, x_value, color="red")
plt.title("x_process")
plt.xlabel('trial')
plt.ylabel('x_new')
ax = fig.add_subplot(1, 2, 2)
y_value = np.array(y_new_list)
plt.plot(trial, y_value, color="blue")
plt.title("y_process")
plt.xlabel('trial')
plt.ylabel('y_new')
plt.show()
投入
$$f(x, y)=\frac{x^{4}}{2}+\frac{x^{3}}{3}-2 x^{2} y+4 x+3 y^{2}+4 y+4$$
secant_method_2val(lambda x,y: (1/2)*x**4+(1/3)*x**3-2*(x**2)*y+3*y**2+3*x-1*y+4,
lambda x,y: 2*x**3+x**2-4*x*y+3,
lambda x,y: 6*y-2*x**2-1,
2.9 ,1.1,
0.7 ,0.6, 0.0001)
========== processing ==========
1回目:x_new = 0.8966608356519854,y_new=1.7789380582176801
2回目:x_new = 0.46072428100335133,y_new=0.09276375276513948
3回目:x_new = 0.3214593587525236,y_new=0.03048594045777645
4回目:x_new = -2.3007446279112482,y_new=-0.5689480801613761
5回目:x_new = -0.1396017347664773,y_new=0.2929760918763705
6回目:x_new = -0.4783746153102301,y_new=0.34421672097573774
7回目:x_new = 1.873658873538518,y_new=-0.16843363867868555
8回目:x_new = -1.0413314148600892,y_new=0.1990416524047588
9回目:x_new = -1.448402437071243,y_new=0.34450415976322235
10回目:x_new = -2.789234057460034,y_new=1.4949228060550759
11回目:x_new = -2.0048205758538753,y_new=1.3471035212103724
12回目:x_new = -2.2523935466685447,y_new=1.782625309639497
13回目:x_new = -2.6623611224707515,y_new=2.4526447430979523
14回目:x_new = -2.547973663834364,y_new=2.328480053986123
15回目:x_new = -2.567727379134939,y_new=2.3629302398098053
16回目:x_new = -2.5702751956843284,y_new=2.368569196737502
17回目:x_new = -2.5702558657988095,y_new=2.3687192279024103
18回目:x_new = -2.5702482888503564,y_new=2.368725428478324
========== Result ==========
solution:x = -2.5702482888503564
solution:y = 2.368725428478324
min_value:-4.382380559808665
答え合わせ
答え合わせに使用した wolframAlpha
https://www.wolframalpha.com/
感想
ニュートン法の時は1変数の時に、分母に来ていた微分が、2変数では行列の-1乗で表すという形になっていて、直感的にもしっくりくる感じです。
セカント法の場合は同じノリ($\nabla f(x,y)$)の差分を取って逆行列で乗り切ろうとする)で実装しようとすると逆行列が見つからない問題で詰まります。
BFGS公式以外にも他にも方法はあるそうですが、うまく考えた人がいると感心してしまいますね。