ロジスティック回帰をIRLSでスクラッチしてstatsmodelの近似結果を得る

IRLS

iteratively reweighted least squares method
反復再重み付け最小二乗法
ニュートンラフソン法

使用したデータ：http://logopt.com/data/hospital.csv

やりたいこと

binaryのresponse variableを持つデータに対してロジスティック回帰の回帰係数を決定する。（今回の説明変数は5つ）

$$log(\frac{1}{1-p})= \beta_0 +\beta_1x_1 +\beta_2x_2 +\beta_3x_3 +\beta_4x_4+\beta_5x_5$$

シグモイド関数：

$\sigma(x)=\frac{1}{1+exp(-x)} $

を用いて、シグモイド関数によって返される値を$\mu_n$とすると
$\mu_n=
\frac{1}
{1+exp\{-(\beta_0+\beta_1x_{n,1}+\beta_2x_{n,2}+\beta_3x_{n,3}+\beta_4x_{n,4}+\beta_5x_{n,5})\}}
=\frac{1}{1+exp(-X\boldsymbol{\beta})}
=\sigma({X\boldsymbol{\beta}})$

この式のパラメータ $\beta_0 〜 \beta_5$ を最適化する。



尤度関数を考えると

$P_n=\mu_n^{t_n}+(1-\mu_n)^{1-t_n}$

＜$t_n=1$の場合＞

$P_n=\mu_n$

これは、$t_n=1$である確率なので

$t_n=1$を正しく予想するためには$P_n$が高いほどよい

＜$t_n=0$の場合＞

$t_n$=0である確率が

$P_n=1-\mu_n$

これは、$t_n=0$である確率なので

$t_n=0$を正しく予想するためには$P_n$が高いほどよい

以上、尤度関数を用いて

どちらの場合においても、正しく予想するためには$P_n$の最大化を目指せばよい。


目的：$P_n$の最大化



尤度関数を用いて

$$L(\beta)=\prod_{n=1}^{N}P_n=\prod_{n=1}^{N} \{\mu_n^{t_n}+(1-\mu_n)^{1-t_n}\}$$

この式の最大化の総乗計算は値が限りなく0に近くアンダーフローになるので両辺の対数を取る

$$-\log L(\beta)=-\sum_{n=1}^{N}t_n\log{\mu_n}+(1-t_n)\log(1-\mu_n)$$

微分すると

$$\frac{dL(\beta)}{d\beta}=\sum_{n=1}^{N}x_n(\mu_n-t_n) $$

これを最大化する$\boldsymbol{\beta}$を求める。

簡単には解けないので、

IRLSを用いて最適な $\boldsymbol{\beta}$を求める

$$\beta_{new}=\beta_{old}-(X^TWX)^{-1}X^T(\boldsymbol{\mu}-\boldsymbol{t})$$

この最後の式を実装する。

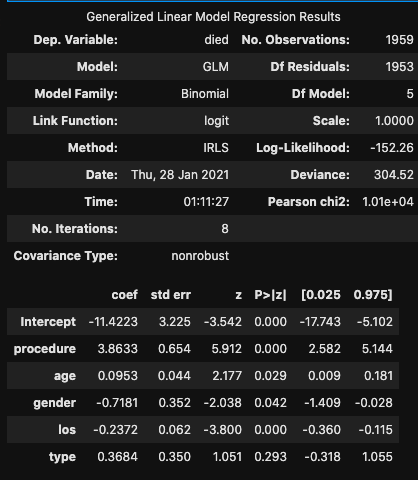
statsmodelの結果

import pandas as pd
df = pd.read_csv("hospital.csv")

# 統計モデル
import statsmodels.formula.api as smf
import statsmodels.api as sm

mod_glm = smf.glm(formula="died~procedure+age+gender+los+type",
                  data = df,
                  family = sm.families.Binomial()).fit()

mod_glm.summary()

IRLSの実装

$$\beta_{new}=\beta_{old}-(X^TWX)^{-1}X^T(\boldsymbol{\mu}-\boldsymbol{t})$$

片っ端から計算していきます。

import pandas as pd
df = pd.read_csv("hospital.csv")
df = df.drop(columns="Unnamed: 0")

import numpy as np
import math
# 学習データを読み込む
data = np.loadtxt('hospital.csv', delimiter=',',skiprows=1, usecols=[1, 2, 3, 4, 5, 6])
#  説明変数
X = data[:,1:len(df.columns)]
# 目的変数
y = data[:,0]

# 初期化されたパラメータ
# b_0 〜 b_4まで
beta = np.random.rand(len(df.columns))

# betaの初期値を修正する関数
def beta_adjust(initial_value):
    for i in range(len(df.columns)):
        beta[i]=initial_value
    return beta

# 説明変数 x_1 〜 x_4 を格納した行列に対して 列 x_0（全て1） を加える関数
def add_x0(x):
    x0 = np.ones([x.shape[0],1])
    return np.hstack([x0,x])

# シグモイド関数に入れて予測値を返す関数
def sigmoid(x,beta):
    return 1/(1+np.exp(-np.dot(x,beta)))


# betaの初期値を与える
beta_adjust(initial_value=0.01)

# X
X_addx0 = add_x0(X)
# Xの転置
X_addx0T = X_addx0.T

# beta依存部分
mu = sigmoid(X_addx0,beta) # sigmoid関数から返る値
diag_mu = np.diag(mu) # muの対角行列
diag_1_mu = np.diag(1-mu) # 1-muの対角行列
# diag_muとdiag_1_muの掛け算からW:mu(1-mu)の対角行列を作る
W = np.dot(diag_mu, diag_1_mu)

Xt_W = np.dot(X_addx0T,W)
Xt_W_X = np.dot(Xt_W,X_addx0)
Xt_W_X_inv = np.linalg.inv(Xt_W_X)
Xt_W_X_inv_X = np.dot(Xt_W_X_inv,X_addx0T)
mu_T = mu-y # muから正解値yを引く部分
renew = np.dot(Xt_W_X_inv_X,mu_T)

print("==========initial value==========")
print(beta)
print("==========processing==========")

# 繰り返し回数
epoch = 10
count = 0

# 繰り返し回数を指定した分IRLSで更新する
for _ in range(epoch):
    beta = beta - renew
    count +=1
    print("{}回目:beta= {}".format(count,beta))
    # beta依存する部分は新しいbetaで更新する
    mu = sigmoid(X_addx0,beta) # sigmoid関数から返る値
    diag_mu = np.diag(mu) # muの対角行列
    diag_1_mu = np.diag(1-mu) # 1-muの対角行列
    # diag_muとdiag_1_muの掛け算からW:mu(1-mu)の対角行列を作る
    W = np.dot(diag_mu, diag_1_mu)

    Xt_W = np.dot(X_addx0T,W)
    Xt_W_X = np.dot(Xt_W,X_addx0)
    Xt_W_X_inv = np.linalg.inv(Xt_W_X)
    Xt_W_X_inv_X = np.dot(Xt_W_X_inv,X_addx0T)
    mu_T = mu-y # muから正解値yを引く部分
    renew = np.dot(Xt_W_X_inv_X,mu_T)

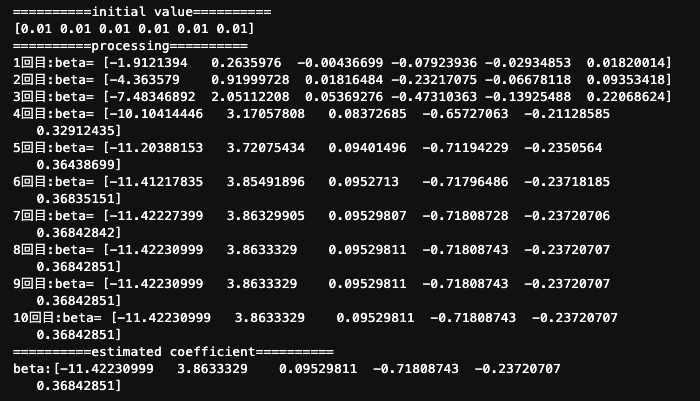
print("==========estimated coefficient==========")
print("beta:{}".format(beta))
print()
print("回帰係数の推定値:Intercept:{},age:{},lwt:{},smoke:{},ptl:{}"
      .format(beta[0],beta[1],beta[2],beta[3],beta[4],beta[5]))
print()
# 標準誤差
var_beta = np.diag(Xt_W_X_inv)
std_error = np.sqrt(var_beta)
print("回帰係数の標準誤差:Intercept:{},age:{},lwt:{},smoke:{},ptl:{}"
      .format(std_error[0],std_error[1],std_error[2],std_error[3],std_error[4],std_error[5]))
print()
# Z_value
z_value = beta/std_error
print("回帰係数のz_value:Intercept:{},age:{},lwt:{},smoke:{},ptl:{}"
      .format(z_value[0],z_value[1],z_value[2],z_value[3],z_value[4],z_value[5]))
print()
# deviance
mu_exp = np.log(mu)
one_mu_exp = np.log(1-mu)
deviance = -2*(np.dot(y,mu_exp)+np.dot(1-y,one_mu_exp))
print("Residual deviance:{}".format(deviance))

出力結果

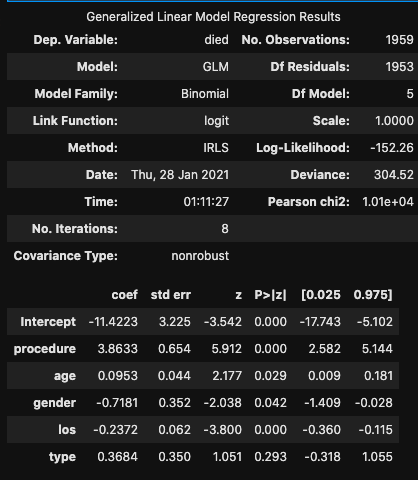
答え合わせ（statsmodelの結果の再掲）

繰り返し回数10回でほぼ誤差なし。

収束しない場合にエラーを吐くようにしたり、繰り返し回数ではなく、誤差で繰り返しが終わるように改善するなど、改善の余地あり。