この記事では、OR-Toolsを使ってJob Shop Scheduling Problem (JSSP)を解くチュートリアルをやってみたので、アウトプットとしてまとめています。
Job shop scheduling problemの概要
Job Shop Scheduling Problem (JSSP)は、複数のジョブとマシンがあり、各ジョブが異なる順序でマシンを使用するという条件の下で、全てのジョブが最短の時間で完了するようにスケジュールを決定する問題です。
JSSPには以下の制約があります
- 各ジョブは、変更できない特定の順序で一連のタスクを実行する
- 各タスクは、指定されたマシンで指定された時間だけ処理される
- 各マシンは同時に1つのタスクしか処理できない
- 各ジョブのタスクは、前のタスクが終了するまで開始できない
これらの制約の下で、全てのジョブが完了する最短の時間(メイクスパン)を見つけることを目的として最適化を行います。
OR-Toolsの概要
OR-Tools は最適化のためのオープンソース ソフトウェア スイートで、車両ルーティング、フロー、整数および線形プログラミング、制約計画における世界で最も難しい問題に対処できます。
前提条件
- Python 3.x がインストールされていること
- or-toolsがインストールされていること
※Google colabを利用するとPythonが準備された状態となるため、OR-Toolsをインストールするだけで済みます。
サンプルコード
jupyter notebookの全コードはGithubを参照してください
githubはここ
1.データの定義
今回はMachine=3, Job=5の条件で最適化を実施する。
# Job情報
jobs_data = [ # task = (machine_id, processing_time).
[(0, 3), (1, 2), (2, 2)], # Job0
[(0, 2), (2, 1), (1, 4)], # Job1
[(1, 4), (2, 3)], # Job2
[(1, 2), (0, 1), (2, 4)], # Job3
[(2, 1), (0, 2), (1, 1)], # Job4
]
# Machineの数
machines_count = 1 + max(task[0] for job in jobs_data for task in job)
all_machines = range(machines_count)
# Taskの合計時間
horizon = sum(task[1] for job in jobs_data for task in job)
2.モデルの作成
OR-ToolsのCpModelというクラスを利用します。
CpModelは制約プログラミング(Constraint Programming)を表現するためのクラスとなります。
# モデルの作成
model = cp_model.CpModel()
3.変数の定義
# Taskの種類
task_type = collections.namedtuple('task_type', 'start end interval')
# 解取り回し用
assigned_task_type = collections.namedtuple('assigned_task_type',
'start job index duration')
# ジョブタスクの処理時間
all_tasks = {}
machine_to_intervals = collections.defaultdict(list)
# 開始、終了、処理時間変数を作成
for job_id, job in enumerate(jobs_data):
for task_id, task in enumerate(job):
machine = task[0]
duration = task[1]
suffix = '_%i_%i' % (job_id, task_id)
start_var = model.NewIntVar(0, horizon, 'start' + suffix)
end_var = model.NewIntVar(0, horizon, 'end' + suffix)
interval_var = model.NewIntervalVar(start_var, duration, end_var,
'interval' + suffix)
all_tasks[job_id, task_id] = task_type(start=start_var,
end=end_var,
interval=interval_var)
machine_to_intervals[machine].append(interval_var)
4.制約の定義
下の2つの制約を追加する
- 各ジョブは、変更できない特定の順序で一連のタスクを実行する
- 各マシンは同時に1つのタスクしか処理できない
# 重複無の制約を追加
for machine in all_machines:
model.AddNoOverlap(machine_to_intervals[machine])
# 実行順序の制約を追加
for job_id, job in enumerate(jobs_data):
for task_id in range(len(job) - 1):
model.Add(all_tasks[job_id, task_id +
1].start >= all_tasks[job_id, task_id].end)
5.目的関数の定義
makespanを最小化する関数として定義
# 目的関数
obj_var = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(obj_var, [
all_tasks[job_id, len(job) - 1].end
for job_id, job in enumerate(jobs_data)
])
model.Minimize(obj_var)
実際に解く
solver = cp_model.CpSolver()
status = solver.Solve(model)
6.結果の確認
if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
print('Solution:')
# Machine毎に割当てられたTaskのリストを作成
assigned_jobs = collections.defaultdict(list)
for job_id, job in enumerate(jobs_data):
for task_id, task in enumerate(job):
machine = task[0]
assigned_jobs[machine].append(
assigned_task_type(start=solver.Value(
all_tasks[job_id, task_id].start),
job=job_id,
index=task_id,
duration=task[1]))
# Machine毎のOutputを作成
output = ''
for machine in all_machines:
# 開始時間でソート
assigned_jobs[machine].sort()
sol_line_tasks = 'Machine ' + str(machine) + ': '
sol_line = ' '
for assigned_task in assigned_jobs[machine]:
name = 'job_%i_task_%i' % (assigned_task.job,
assigned_task.index)
# スペース挿入
sol_line_tasks += '%-15s' % name
start = assigned_task.start
duration = assigned_task.duration
sol_tmp = '[%i,%i]' % (start, start + duration)
# スペース挿入
sol_line += '%-15s' % sol_tmp
sol_line += '\n'
sol_line_tasks += '\n'
output += sol_line_tasks
output += sol_line
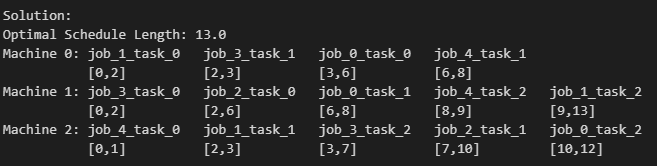
print(f'Optimal Schedule Length: {solver.ObjectiveValue()}')
print(output)
else:
print('No solution found.')
最適化の結果、13時間で全ての作業が完了できるスケジュールが完成しました。
まとめ
OR-Toolsを使ってJSSPを解くチュートリアルを実施した内容をOutputとしてまとめました。JSSPのような複雑な問題も数Stepのコーディングで解が得られるため、非常に有用なツールだと感じました。
JSSPはNP困難な問題として扱われることがあるため、ヒューリスティック手法や機械学習を用いた手法についてもリサーチ予定です。