概要
MATLABもしくはOctaveのtf関数を使った伝達関数ベースのシミュレーションについて紹介します。tf関数を使えば、伝達関数を直感的に記述でき、それをベースとする制御対象の解析や制御器の設計を簡単に実行できるようになります。
sってどうやって実装するの?
古典制御を勉強すると、伝達関数なるものが登場し、$s$ってなんだ?と圧倒されるのではないでしょうか。その後は、伝達関数を主体とする一次遅れ系やPIDコントローラの時間/周波数応答をとりあえず学習し、「完全に理解した」となります。しかし、いざ自分がそれを使った解析や設計をしようとする頃には、「$s$ってどうやって実装するんだっけ?」となります。
おそらく、こんな体験をするのは私だけかもしれませんが、以下のような手順で実装できる段階までガリガリ計算すれば実行できます。
- (時間応答)伝達関数を逆ラプラス変換 → 常微分方程式 → Runge–Kutta method etc.
- (周波数応答)$s$は複素数であり周波数 → $s=j\omega$と代入 → $\omega$に関するゲインと位相を計算
MATLAB/Octaveのtf関数を使って
しかしながら、「せっかく理解した伝達関数とはいったい...」、「えっ、閉ループ伝達関数みたいな高次の伝達関数もガリガリするの?」みたいなときどうするのか。また、とりわけプロセス制御のような古典制御がメジャーな分野では、伝達関数をベースに思考したり、試行したりすることから、前パラグラフのような手段だと非効率的です。シミュレーションだけが目的なら、ちょちょいでできるMATLABやOctaveのような数値計算専門の言語を使うべきで、tf関数がその手助けをしてくれます。
①準備
- MATLABの「Control System Toolbox」が必要。有料(大学生なら無料で使えたり)。
- Octaveの「control」パッケージが必要。無料。
②一般的な伝達関数の実装
- 記述したい伝達関数は
$$P(s) = K\frac{b_ms^m+\ldots+b_1s+1}{a_ns^n+\ldots+a_1s+1}e^{-Ls}$$
ただし、$K$はゲイン、$L$はむだ時間です。
-
コードは
P = K*tf([bm,..,b1,1], [an,..,a1,1],'IODelay',L,'Variable','s'); -
引数は
- 1番目は分子多項式、2番目は分母多項式の係数をそれぞれ降べきの順にベクトルで指定。
- 3番目$^{\star1}$以降は必要に応じて追加するプロパティで、'プロパティ名'とその'値'セットで指定。今回は、3と4番目にむだ時間$L$を、5と6番目に明示的に連続時間領域の伝達関数であること$^{\star2}$を指定しました。
$^{\star1}$・・・離散時間領域の伝達関数を扱いたいときは3番目にサンプリング時間を指定し、4番目以降からプロパティとなります。ここでは詳細は割愛。
$^{\star2}$・・・省略可。
解析と設計をしよう
ここでは、MATLAB/Octaveを使って実例を交えた制御系の解析と設計を示したいと思います。
制御対象のモデリング
制御対象を以下のような「一次遅れ+むだ時間」系のモデル
$$
P(s) = \frac{K}{1+Ts}e^{-Ls}
$$
でモデリングし、そのとき、$K=0.5$、時定数$T=40.0$、$L=8.0$と推定したものとします。モデリングした制御対象の記述は以下のコードの通りで、留意点として、Octaveの場合、'IODelay'プロパティが実装されていないようで、パディ近似等を代用しないとむだ時間が表現できないようです(MATLAB最強...)。
% 推定した制御対象のモデル
K = 2.0;
T = 40.0;
L = 8.0;
P = tf(K,[T,1],'IODelay',L); % MATLABの場合
P = tf(K,[T,1])*tf([-L/2,1],[L/2,1]); % Octaveの場合(一次で近似)
制御器の設計
続いて、制御器として不完全微分付きPIDコントローラ
$$
C(s) = k_p\Bigl(1+\frac{1}{T_is}+\frac{T_ds}{1+0.125T_ds}\Bigr)
$$
を設計し、制御対象の自動化をするために、PIDパラメータの調整法はChien, Hrones and Reswick法(オーバーシュート量0%の目標値追従)を使います。制御器の記述は以下のコードの通りです。
kp = 0.6*T/K/L;
Ti = 1.2*T;
Td = 0.5*L;
C = kp*(1+tf(1,[1,0])/Ti+Td*tf([1,0],[0.125*Td,1]);
シミュレーション
以下は、Octaveによるシミュレーション結果です。(MATLABほしい)
- 安定性の確認
開ループ伝達関数$P(s)C(s)$に基づくゲイン余裕と位相余裕のプロット
margin(P*C);

-
目標値$r$から制御量$y$までの閉ループ伝達関数$\frac{P(s)C(s)}{1+P(s)C(s)}$に基づくステップ状目標値変更の際の時間応答
step(PC/(1+PC));
<img src="https://qiita-image-store.s3.amazonaws.com/0/317923/3dcea1a8-a0de-e75f-20df-89fa160d8c95.png" width=70%>
なお、step関数は時間領域の伝達関数が厳密にプロパでなければシミュレーションできません。
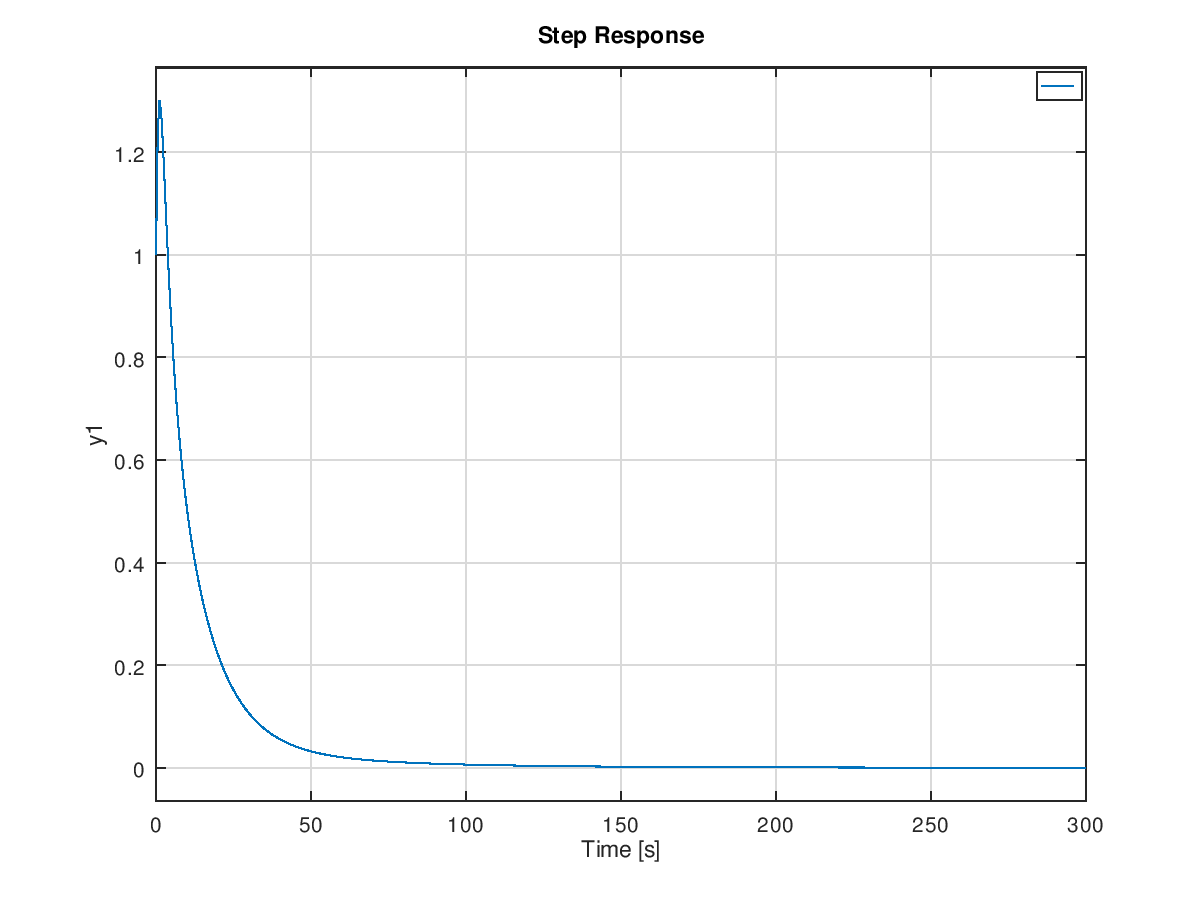
- 出力端外乱$d$から制御量$y$までの閉ループ伝達関数$\frac{1}{1+P(s)C(s)}$に基づくステップ状外乱印可の際の時間応答
```octave:
step(1/(1+P*C));
まとめ
tf関数を使った伝達関数の記述方法とそれを使ったシミュレーションを示しました。tf関数で制御対象$P(s)$と制御器$C(s)$を最低限定義すれば、あとは四則演算で各種伝達関数を計算し、step関数でステップ状の信号に対する時間応答や、今回は説明しなかったbode関数を使うことで感度関数/相補感度関数などの周波数応答を解析(プロット)することができます。
参考
- tf関数のMATLABの公式ドキュメント
- 現代制御で登場する状態空間表現を扱いたいときは、ss関数を使います。