三段論法をプログラミングしてみたかった話

こんにちは！ Life is Tech! メンターのりっしーです。

いきなりですが、私には小さな夢がありました。「三段論法をプログラミングしてみたい」
人間の思考過程を自分でコード化できたら楽しそうだなと思っていた頃、大学の論理学の講義で半年間ひたすら三段論法について学ぶという、少し珍しい経験をしたことがきっかけです。ということで、今回の記事では三段論法を実装していきます！だいぶ渋いテーマですが、プログラミングでこんなこともできるんだな、と思ってもらえたら嬉しいです。

##予備知識： 三段論法のパターン
三段論法(syllogism)とは、論理学における推論型式の一つです。
概念を言葉で表したもの を論理学では名辞というのですが、
三段論法には、大名辞(論証の結論の述語)、小名辞(論証の結論の主語)、中名辞(大名辞と小名辞を関連づける名辞)が登場します。
有名な例を一つ挙げます。

前提1：どの人間も死ぬものである。
前提2：ソクラテスは人間である。
結論：したがって、ソクラテスは死ぬものである。

この例の場合、大名辞は「死ぬもの」、小名辞は「ソクラテス」、中名辞は「人間」となります。
この三段論法は形式的に妥当なので、たとえば、小名辞「ソクラテス」を「アリストテレス」や「プラトン」に置き換えても、正しい結論が得られるという特徴があります。

私たちの日常生活では、形式を意識して三段論法を使う機会はほぼないと思います。
実は、形式的に妥当な三段論法は、24パターンも存在するんです。意外と沢山ありますね！
（Wikipediaに全パターンのベン図をまとめた表があったので紹介しておきます)

このことから、三段論法をプログラミングするときには、24通りの何らかの処理が必要となることが予想できます。

では、実際にプログラミングしていきましょう！！と書きたいところですが、
今回使用する言語はPrologです。馴染みのない人が多いと思うので、Prologについての説明を少しだけ挟みます。
#予備知識： Prologについて
Prolog（プロログ：Programming in Logic）は、論理型言語に分類されます。
Prologについての説明は、このブログ記事がシンプルで分かりやすかったので、以下に一部引用します。

Prolog のプログラムは次の３つの要素から成ります．
＊事実: 事物とその関係についていくつかの事実を宣言する．
＊規則: 事物とその関係についての規則を定義する．
＊質問: 事物とその関係について質問する．

たとえばPrologを用いて、「クリスマスは12月25日である」という事実を宣言すると、
「クリスマスはいつか?」という質問に対して「12月25日」と答えられるようになります。

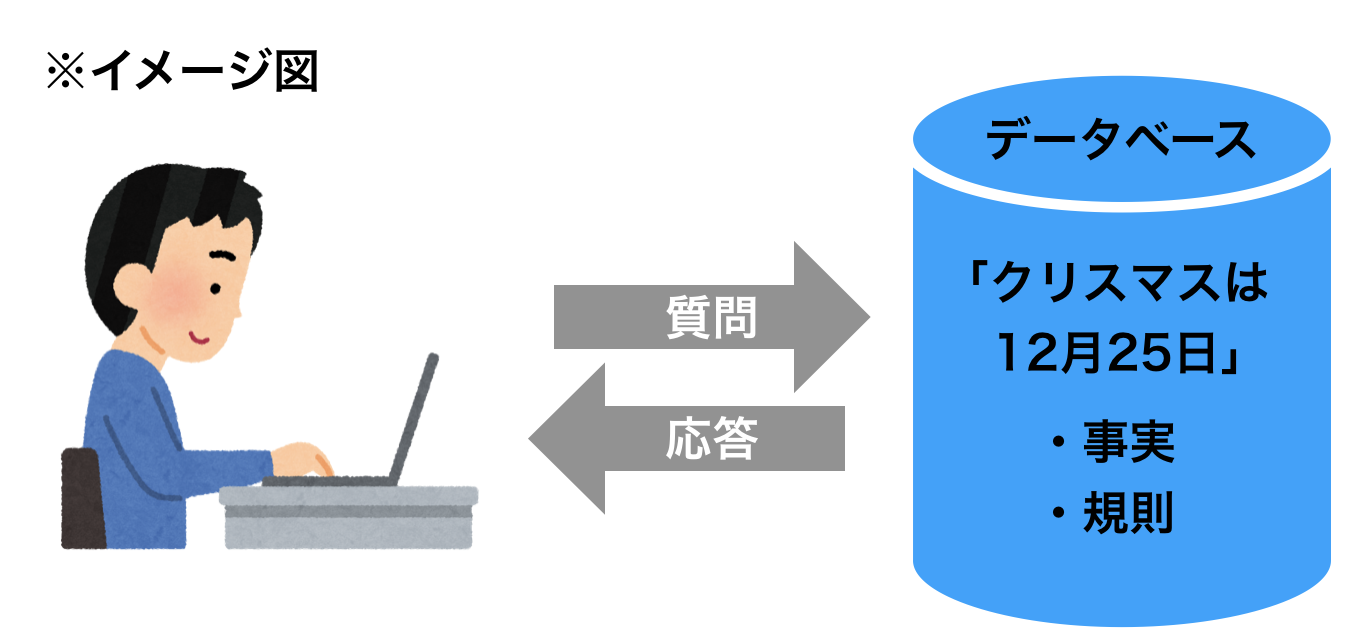
ポイントは、
従来の手続き型言語では「どのように計算するのか? (How)」を考えていたのに対して、
Prologをはじめとする宣言型言語(論理型言語や関数型言語のこと)では「何を計算するのか? (What)」を考えていくということです。

#Prologを用いた三段論法プログラム
ついに、プログラムを作成/実行する段階まできました！

「何を計算するのか」を、具体的にどうやって書いてくべきか、参考になりそうなヒントを探していたところ、21.1 Syllogisms in Prolog: Questionですでに実装済みのコードを見つけました。今回はそのコードを利用します。
###ソースコードとその説明

syllogisms.swi

/* 事実　(三段論法の24パターンを宣言) */
syll(all(M,P), all(S,M), all(S,P)).
syll(no(M,P),all(S,M),no(S,P)).
syll(all(M,P),some(S,M),some(S,P)).
syll(no(M,P),some(S,M),some_not(S,P)).
syll(all(M,P),all(S,M),some(S,P)).
syll(no(M,P),all(S,M),some_not(S,P)).
syll(no(P,M),all(S,M),no(S,P)).
syll(all(P,M),no(S,M),no(S,P)).
syll(no(P,M),some(S,M),some_not(S,P)).
syll(all(P,M),some_not(S,M),some_not(S,P)).
syll(all(P,M),no(S,M),some_not(S,P)).
syll(all(P,M),some_not(S,M),some_not(S,P)).
syll(all(M,P),all(M,S),some(S,P)).
syll(some(M,P),all(M,S),some(S,P)).
syll(all(M,P),some(M,S),some(S,P)).
syll(no(M,P),all(M,S),some_not(S,P)).
syll(some_not(M,P),all(M,S),some_not(S,P)).
syll(no(M,P),some(M,S),some_not(S,P)).
syll(all(P,M),all(M,S),some(S,P)).
syll(all(P,M),no(M,S),no(S,P)).
syll(some(P,M),all(M,S),some(S,P)).
syll(no(P,M),all(M,S),some_not(S,P)).
syll(no(P,M),some(M,S),some_not(S,P)).
syll(no(P,M),some(M,S),some_not(S,P)).

/* 規則　(＝「2つの前提の順序は、導き出される結論に無関係である」 )*/
deduction(P1,P2,C):- syll(P1,P2,C).
deduction(P1,P2,C):- syll(P2,P1,C).

(コードの詳しい説明は今週末に加筆します。すみません)
###実行手順

今回は、Prologのオンライン実行環境であるSWISHを使用します。
前準備として、Programボタンをクリックします。

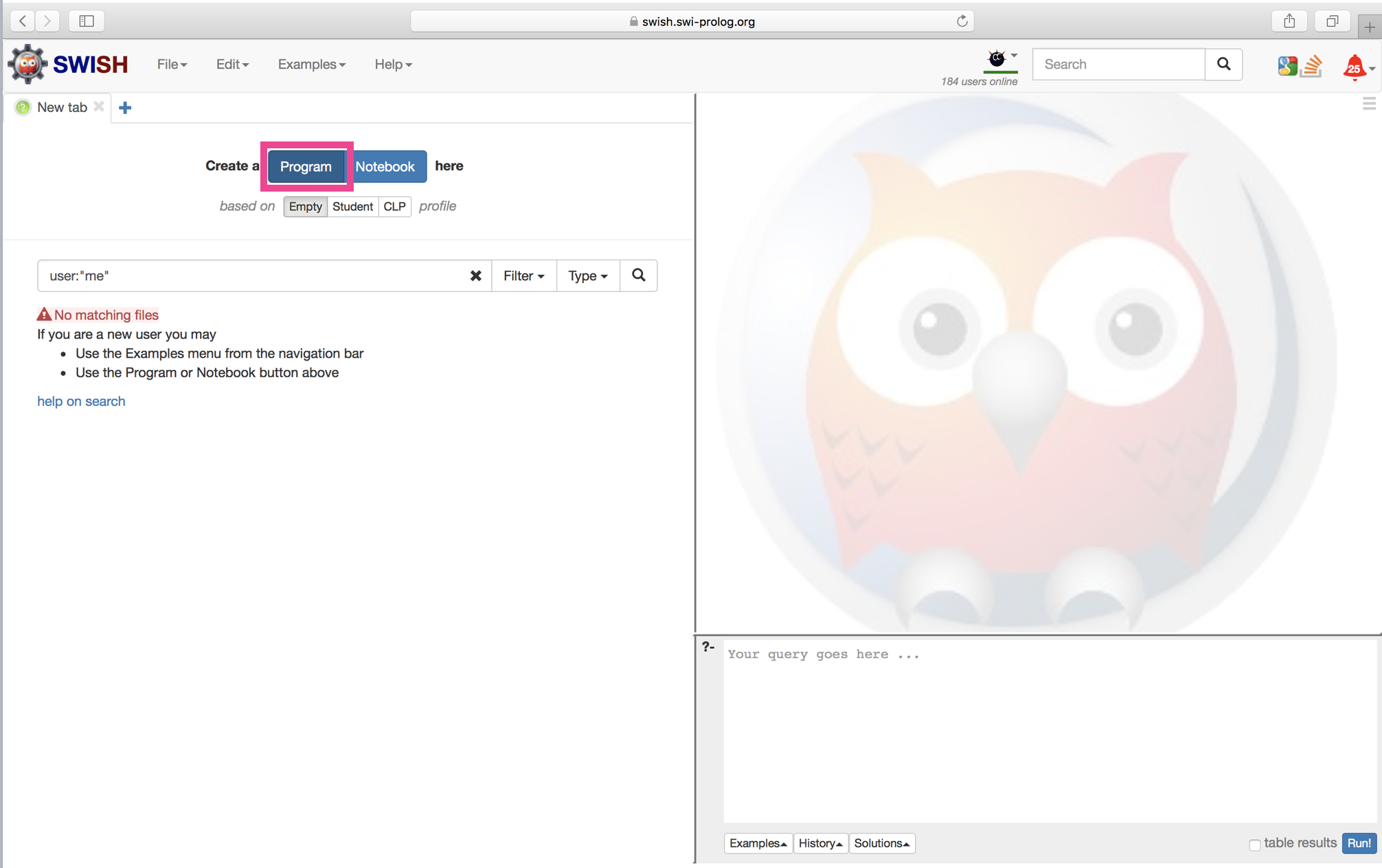
すると、プログラムを記述できるタブが出現します。(画面左)
それを確認したら、①事実と規則(syllogisms.swi)を入力し、②質問を入力します。

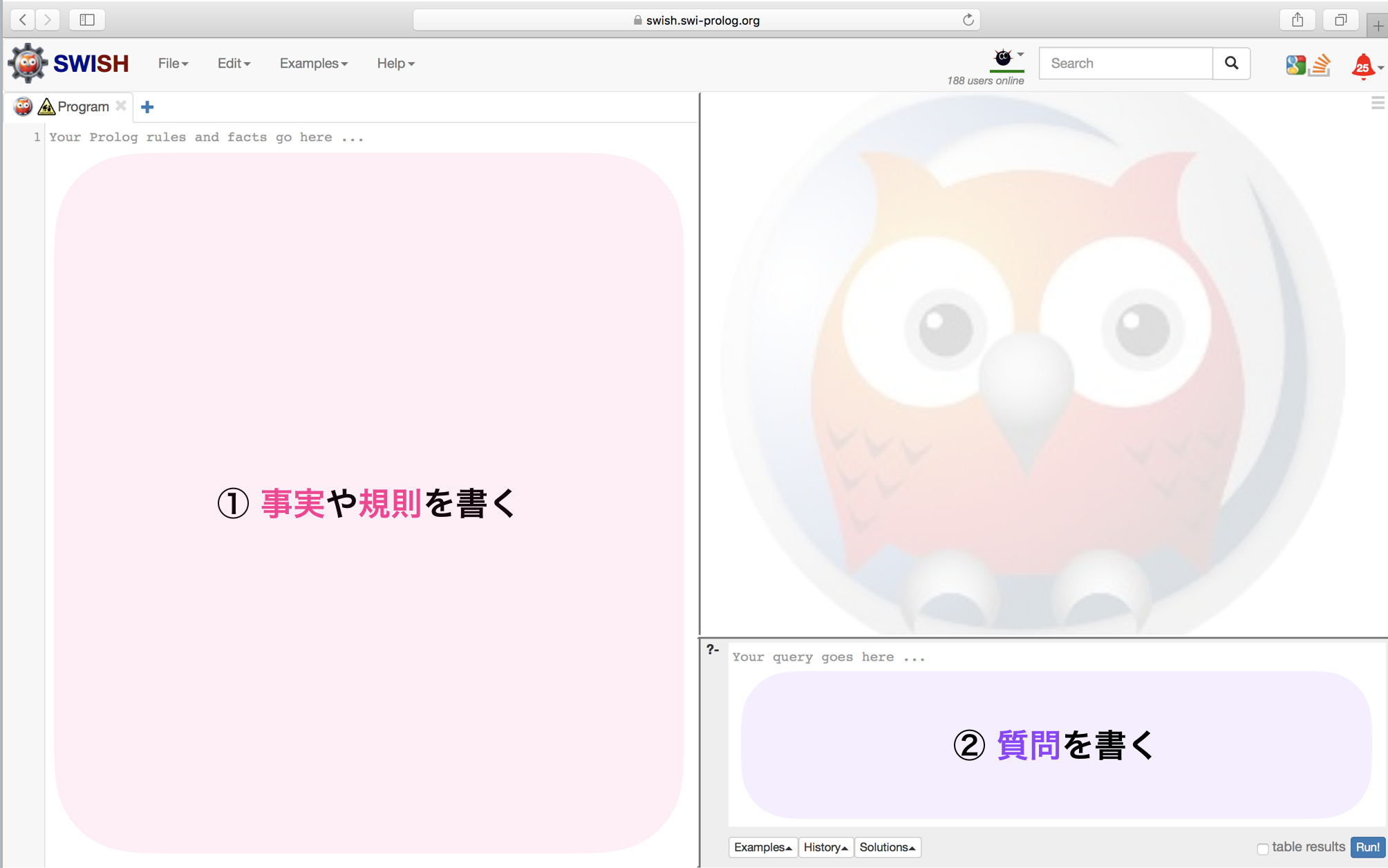
ちなみに、②で入力する質問とは、三段論法における2つの前提のことを指します。
入力方法さえ守れば、どのような2つの前提に対しても対応できるのですが、今回は次のように入力してみます。

deduction(some_not(dogs, cat_hater), all(dogs, mammals), C).

この時点で、画面は次のようになっているはずです。

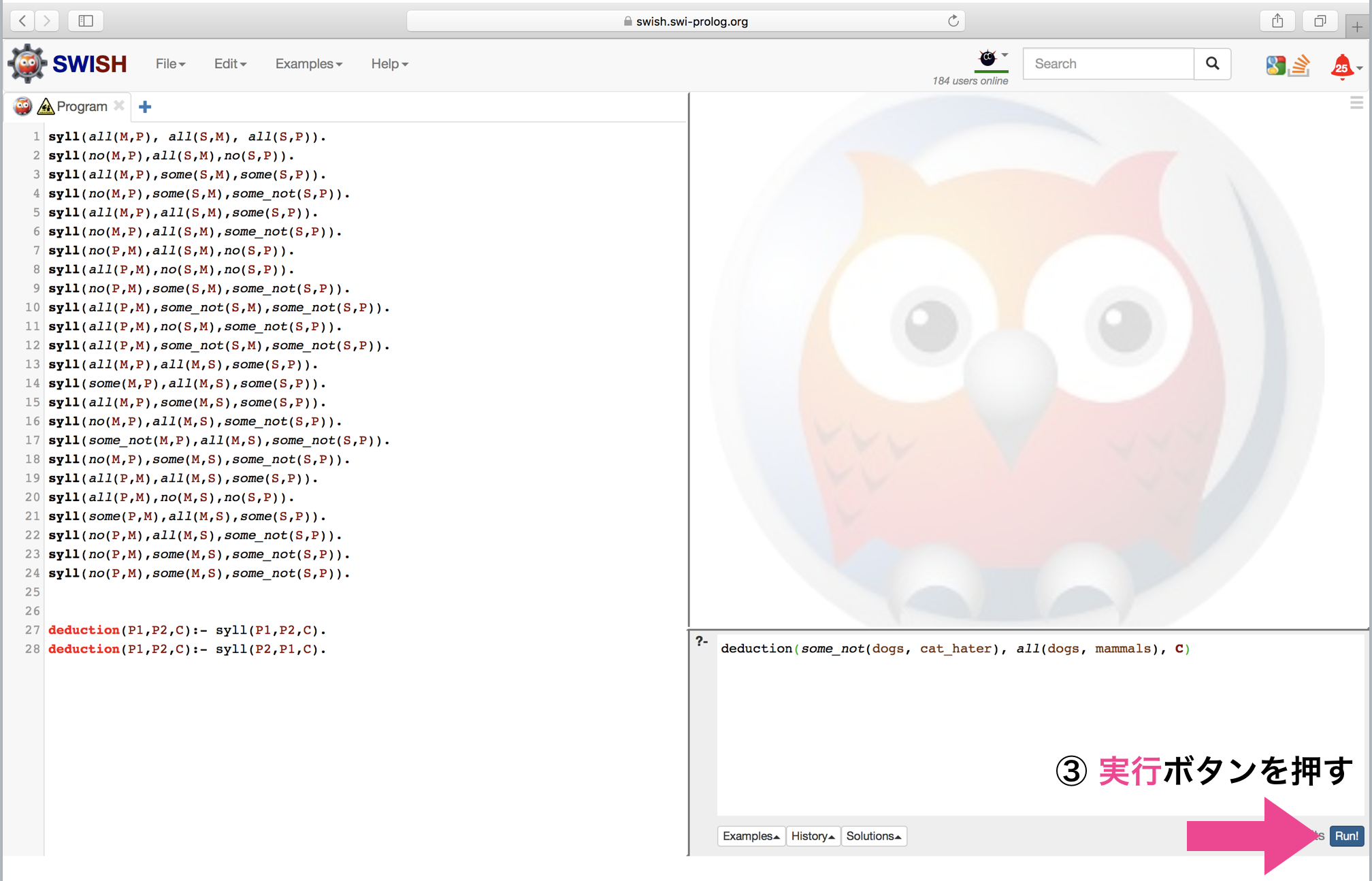
そこで、③実行ボタンを押すと、以下のような実行結果が得られます。

C = some_not(mammals, cat_hater)

###実行結果の解説
質問 「-? deduction(some_not(dogs, cat_hater), all(dogs, mammals), C).」
に対し、
推論の結果「C = some_not(mammals, cat_hater)」
を得ることができました！
これが意味していることは、次のとおりです。

前提1：ある犬は、猫嫌いではない。
前提2：あらゆる犬は、哺乳類である。
結論：したがって、ある哺乳類は、猫を嫌いでない。

##まとめ
三段論法の推論をコンピュータ上で実行することができました！
実際に動かしてみると、意外と面白いので、時間のあるときにぜひ遊んでみてください！

アドベントカレンダーを楽しみにしながら、クリスマスまでを過ごそうと思います
（記事の後半にかけて説明が少し雑になってしまったので、週末に加筆修正します）