概要
今回のコードはGithubにあげています。
ひとことだけ
バンディットアルゴリズムの概要、トンプソンサンプリングの説明、確率系のお話(ベータ分布etc)は他に素晴らしい記事がたくさんあるのでそちらにゆずるとして、自分が感じたトンプソンサンプリングのイメージを文字で紹介して終了とします(笑)。
トンプソンサンプリングの良いところとしては、これまで探求してきた各アームに対して成功回数・失敗回数を記憶しておくことによってアームの選択に反映することができるという点があります。
回数がどのように影響してくるか、ということに関してはベータ分布やベイズ推定のような数学(確率)の知識が必要になってきます。
下のベータ分布のシミュレーションで書いているように、成功・失敗の回数によってグラフの形状が変化してきます。
グラフを捉える際のイメージとしては、 グラフとX軸で囲まれた領域では、その事象が一様に起こり得る という感じで捉えると入ってきやすいと思います。
言い換えると、囲まれた領域から点を選ぶことができて、その点のXの値 = 事象が起こる確率という風に捉えることができます。
トンプソンサンプリングでは、そのような処理を各アームに対して行なっており、各アームからランダムに選んだ 確率 の中で最大のアームを次に引くようになっています。
成功回数が多ければ高い確率の部分の面積が大きくなり、失敗回数が多ければ低い確率の部分の面積が大きくなる、というイメージです。
つまり、成功した回数が多ければ多いほど選択されやすくなる (= これまでの経験を活かした選択ができるようになる)ということです。
ベータ分布のシミュレーション
ベータ分布のシミュレーションはこちらをやってみるといい。
a: 1, b: 1
成功: 0回 / 失敗: 0回のグラフ。どの確率(X軸)も一様に起こりうる、と言う風に見るらしい。

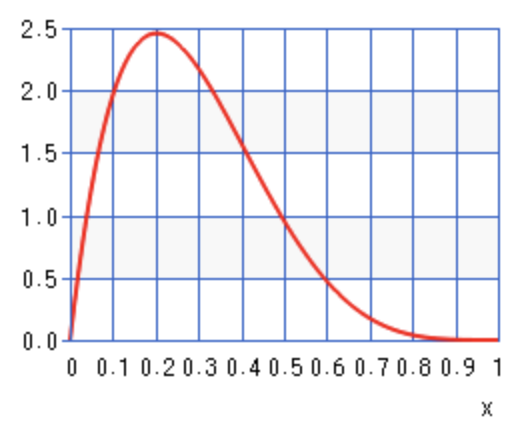
a: 5, b: 2
成功: 4回 / 失敗: 1回のグラフ。グラフの右側の面積が大きい。X軸とグラフで囲まれた部分から事象が起こり得ると見るとわかりやすい。

a: 2, b: 5
成功: 1回 / 失敗: 4回のグラフ。さっきの逆。
参考資料
さいごに
数学的な詳しいことはあまりわからなかったので、追記していただける方いたらリクエスト送ってください!! (イメージ重視の説明が望ましいです)