【SIGNATE】銀行の顧客ターゲティングで勾配ブースティングはランダムフォレストに勝てるのか？

8月から機械学習の学習を始め、一つの区切りとしてQiita課題であるSIGNATEの銀行の顧客ターゲティングに取り組んでみました。
今回のデータ分析のプロセスはAI_STANDARDにのっとって行います。
#1 業務理解
本課題は予測モデルの構築の練習課題として提供されており、実際のビジネス現場からのデータを参考に効率的なマーケティングキャンペーンのためのモデリングを行います。
#2 データの理解

●説明変数の確認
必要なライブラリをインポートし、学習用データ・検証用データ・提出用データをそれぞれ読み込みます。

#ライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.ensemble import GradientBoostingClassifier as GFC
from sklearn.model_selection import GridSearchCV
%matplotlib.inline

#データの読み込み
train=pd.read_csv('train.csv')
test=pd.read_csv('test.csv')
submit_sample=pd.read_csv('submit_sample.csv')

#データ数の確認
print(train.shape)
print(test.shape)

#(27128, 18)
#(18083, 17)

学習用データでは27,168名、検証用データでは18,083名の顧客データが含まれており、キャンペーンの結果（口座開設の有無）が含まれているのは学習用データのみです。予測に使われる17の変数（予測変数）を出力してみます。

train.columns

#Index(['id', 'age', 'job', 'marital', 'education', 'default', 'balance', 'housing', 'loan', 'contact', 'day', 'month', 'duration', 'campaign', 'pdays', 'previous', 'poutcome', 'y'],dtype='object')

それぞれについてコンペサイトの説明を見てみます。

ヘッダ名称	説明
id	行の通し番号
age	年齢
job	職種
soldout	未婚/既婚
education	教育水準
default	債務不履行があるかどうか（yes/no）
balance	年間平均残高（€）
housing	住宅ローン（yes/no）
loan	個人ローン（yes/no）
contact	接触方法
day	最終接触日
month	最終接触月
duration	最終接触時間（秒）
campaign	現キャンペーンにおける接触回数
days	経過日数：前キャンペーン接触後の日数
previous	接触実績：現キャンペーン以前までに顧客に接触した回数
poutcome	前回のキャンペーンの成果
y	定額預金申し込みの有無（1:有り,0:無し）

ただしyというカラムは目的変数であり、検証用データには含まれていません。

●データの中身の確認
⚪︎数量データ
id, age, balance, day, duration, campaign, days, previous, y
○カテゴリデータ
・job ：種類は多岐にわたる
・soldout ：married（既婚）,single（独身）,divorced（離婚）の3種類
・education：primary（初等教育）,secondary（中等教育）,tertiary（高等教育）の3種類
・default ：yes, noの2種類
・loan ：yes, noの2種類
・month ：jan〜decの12種類
・poutcome ：success（成功）, failure（失敗）の2種類

●データの観察
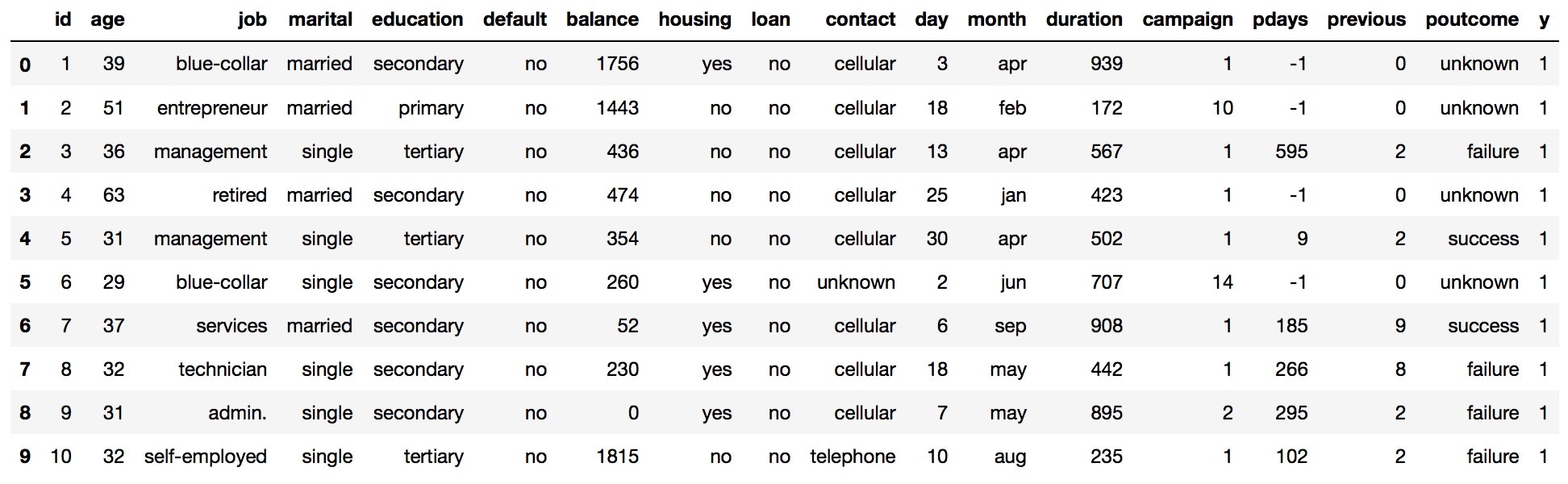
学習用データ、検証用データ共に最初の10人分のデータを見てみます。

train.head(10)

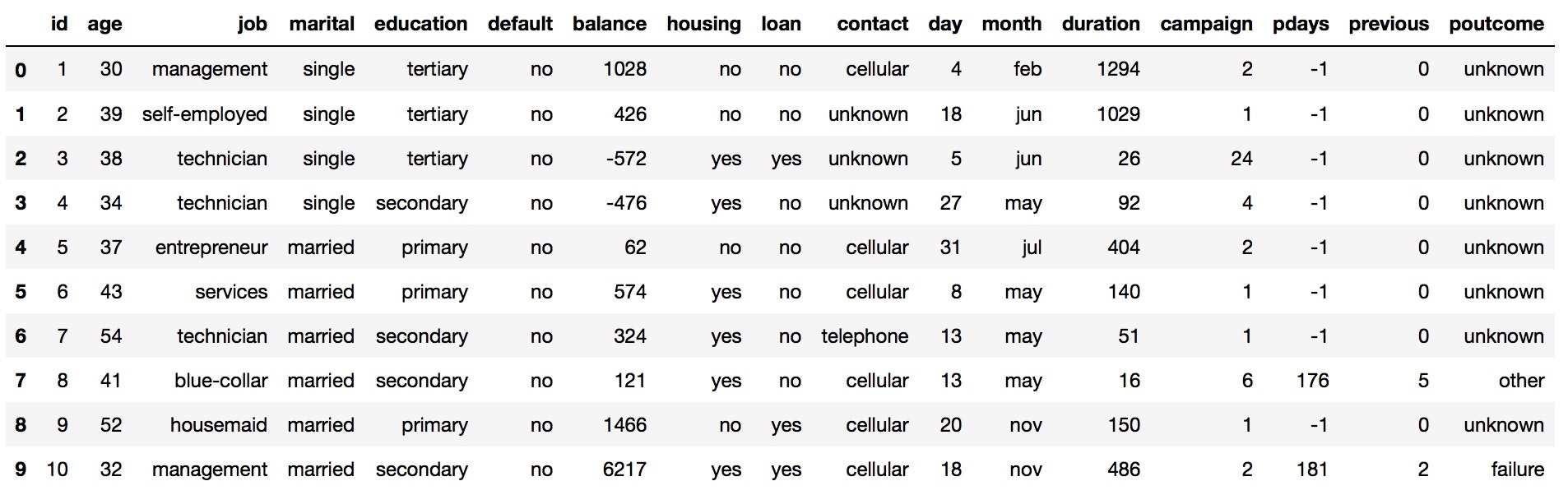
test.head(10)

職業の種類が多そうです。
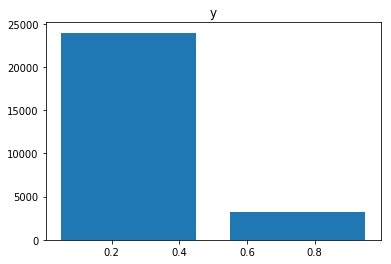
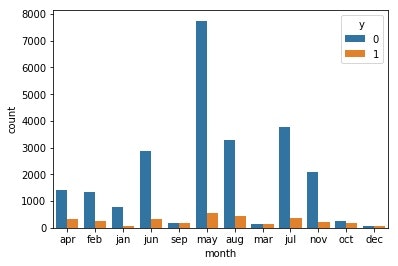
目的変数の分布を見ていきます。

plt.title()
plt.hist(train['y'],bins=2,rwidth=0.8):

train['y'].value_counts()
#0    23954
#1     3174
#Name: y, dtype: int64

預金申し込みをしなかった人（0）とした人（1）の比は概ね8:1で預金申し込みをしなかった人の割合が大半を占めているようです。

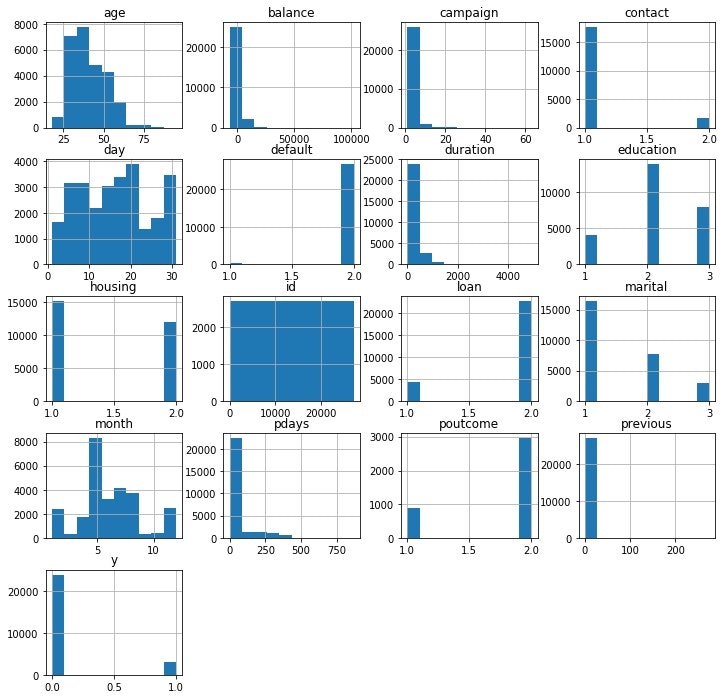
各説明変数とデータの分布を見ていきます。

train.hist(figure=(12,12))

いくつかデータ数に偏りが見られた説明変数について観察を加えます。
・age：年齢層の低い人のデータが多いようです
・contact：接触手段は携帯電話が多い
・default：債務不履行のない人がほとんど
・education：教育水準は中レベルの人が全体の半分ほど
・loan：個人ローンのない人が多い
・marital：結婚している人が多く、未婚、離婚と次ぐ
・month：初夏の時期（5月くらい）が突出して多い。年度の初めだからか？

#3 データの前処理
●カテゴリデータの数量化
以下のような方針でデータの分析が可能な形に変形します。
・ダミー変数化→データの種類が多岐にわたるjobデータ
・マッピング→soldout, education, default, loan, contact, month, poutcome

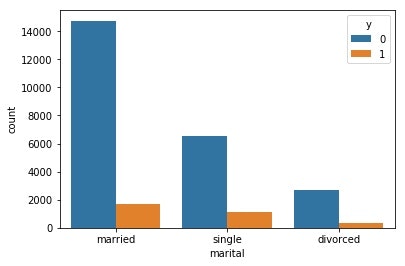
sns.countplot(x='soldout',hue='y',data=train)

soldoutはsingle（独身）とdivorced（離婚）は独り身であることに変わりはないのではないかと思いましたが、ヒストグラムで明示すると差異が見られたので両者は同一には括らないこととしました。

●欠損値の補充
全て数量データに置き換えられたところで欠損値の確認を行います。

print('trainデータの大きさ' + str(train.shape))
train.isnull().sum()

#trainデータの大きさ(27128, 18)
Out[226]:
id               0
age              0
job              0
marital          0
education     1137
default          0
balance          0
housing          0
loan             0
contact       7861
day              0
month            0
duration         0
campaign         0
pdays            0
previous         0
poutcome     23273
y                0
dtype: int64

print('testデータの大きさ' + str(test.shape))
test.isnull().sum()

#testデータの大きさ(18083, 17)
Out[227]:
id               0
age              0
job              0
marital          0
education      720
default          0
balance          0
housing          0
loan             0
contact       5159
day              0
month            0
duration         0
campaign         0
pdays            0
previous         0
poutcome     15526
dtype: int64

欠損値が存在するのはpoutcome, contact, educationの3種類でした。

#前回のキャンペーンの成果と目的変数の相関
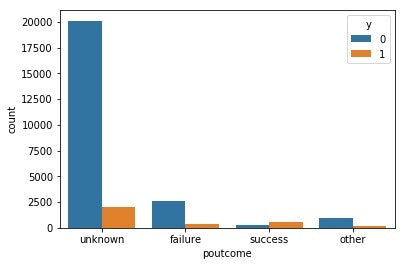
sns.countplot(x='poutcome',hue='y',data=train)

poutcomeについて上のヒストグラムを見ると、前回失敗した場合に今回も失敗した条件付き確率が高く、また前回成功した場合に今回も成功した場合も同様に高くなりました。前回獲得できた顧客は大事なお客様になり得るということでしょう。
しかし重要なデータでありながらも、欠損値の割合がほとんどであるため今回はカラム自体を削除することとしました。

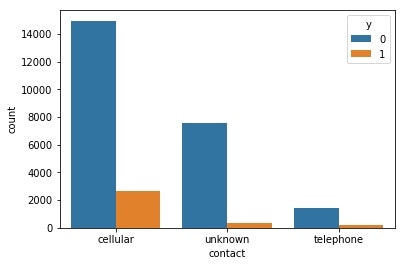
#接触方法と目的変数の相関
sns.countplot(x='contact',hue='y',data=train)

contactについても上のヒストグラムを見ると、携帯電話で連絡を取った場合に比べ、固定電話で連絡を取ったほうが成功する条件付き確率が高くなるようです。携帯電話で応対するお客さんより、家の固定電話で応対するお客さんの方が落ち着いて話を聞いてくれる傾向にあるのでしょうか。
しかし、こちらもpoutcome同様に欠損値が多いのでカラムごと削除しました。

educationは欠損値が比較的少なくかつjobなどとの相関を予測して回帰補充しました。

●数値データのカテゴリ分け
上のようにダミー変数化、カテゴリーデータの数値データへの変換、欠損値の補充など最低限必要なデータの前処理は終了しました。ここでデータの観察の際に相関が見られた、元から数値データであるage, monthの2つの説明変数について詳しく見てみます。

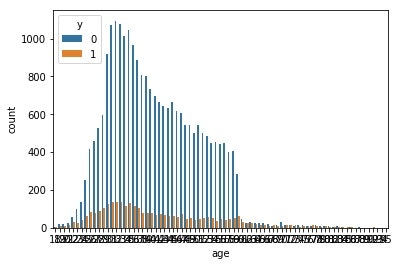
#年齢と目的変数の相関
sns.countplot(x='age',hue='y',data=train)

上の図では見づらくなってしまいますが、20歳以下の若者と60歳以上の高齢者を含む集団は口座の開設率が高いようです。20歳以下の若者は口座の新規開設が多いのではないでしょうか。
よって20歳以上60歳以下の年齢の人々を0,それ以外の人々を1とカテゴリーに分類します。

#最終接触月と目的変数の相関
sns.countplot(x='month',hue='y',data=train)

いくつかの月で著しく口座開設率が低そうです。具体的にはその年や年度の後半の月が多く、始めより顧客も何かを一新する気持ちにはならないのでしょうか。3月、9月、10月、12月を1、その他の月を0とマッピングすることにしました。

#4 手法選択

SIGNATEのサイトからコンペ参加者の分析手法を見てみると、決定木、ランダムフォレスト、ロジスティック回帰が過半数を占めているようです。

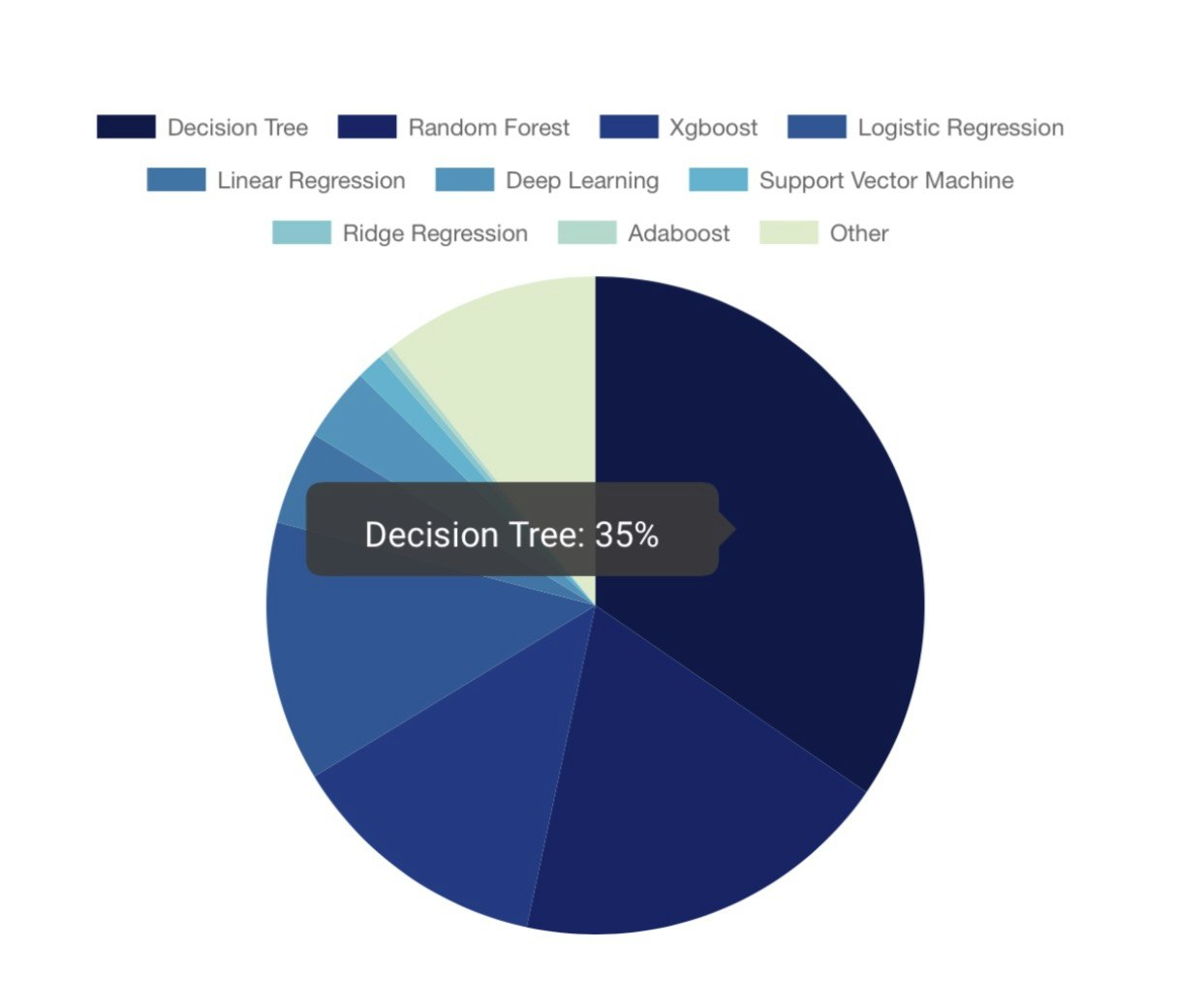
決定木で起きがちな過学習を抑える手法としてランダムフォレストは代表的ではありますが、同時に勾配ブースティング木も頻繁に取り上げられます、
今回は勾配ブースティング木でランダムフォレストより高い精度を出すことは可能なのか、というテーマの下、回帰アルゴリズムとして代表的なロジスティック回帰、分類アルゴリズムとして代表的な決定木の2通りの方法で分析し、さらにツリーベースを軸に決定木の汎化性能を高めたランダムフォレストと勾配ブースティング木を用いて精度の向上を図ります。

#5 学習
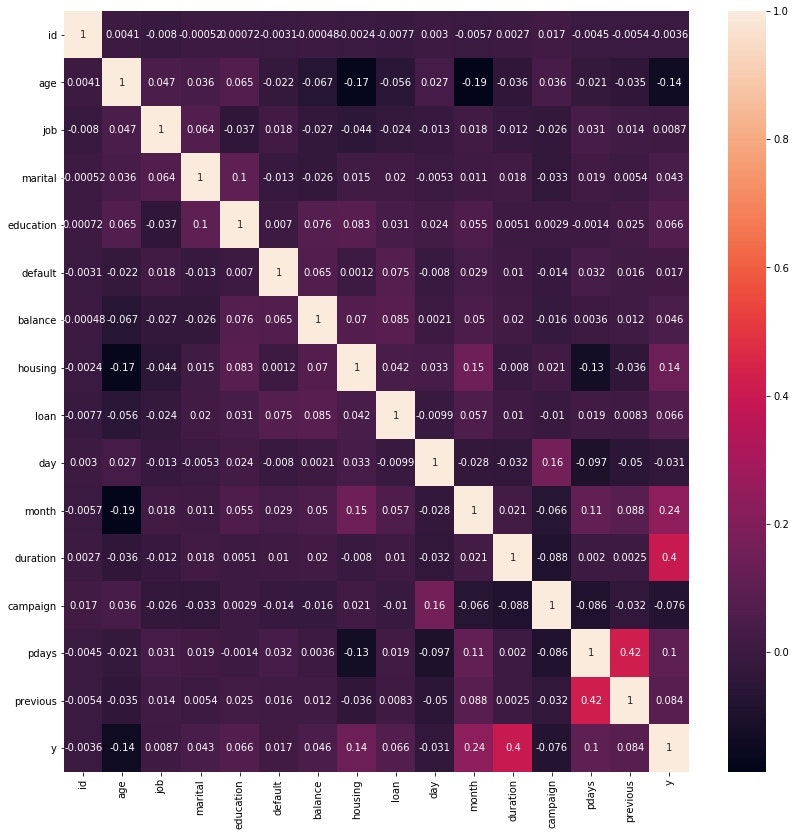
相関係数を算出し、ヒートマップを用いて図示します。

put.figure(figsize=(14,14))
sis.heatmap(ip.corr(),annot=True)

目的変数yとその他各説明変数との相関を見てみると、相関係数が絶対値0.05の説明変数を相関係数が高い順に並べると
duratuon, month, housing, age, pdays, previous, campaign, education, loan
という順が見て取れます。今回はduration, month, housing, age, pdays, previous, campaignを説明変数として用います。

#説明変数と目的変数を指定
X = ip.loc[:, ['duration','month','housing','age','pdays','campaign','previous']].values
y = ip.loc[:,['y']].values
#scikit-learnの仕様に合わせて、一列のベクトルに変換
y = y.reshape(-1)

#データの標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
X_std=scaler.transform()

#データセットの分割
from sklearn.model_selection import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(X_std,y,test_size=0.3,random_state=0)

●ロジスティック回帰

#ロジスティック回帰の実行
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1.0)
lr.fit(Xtrain,ytrain)
#正答率の出力
print('train acc: %.3f' % lr.score(Xtrain, ytrain))
print('test acc: %.3f' % lr.score(Xtest, ytest))

train acc: 0.893
test acc: 0.889

●決定木

#決定木による学習
from sklearn.tree import DecisionTreeClassifier
tree_1 = DecisionTreeClassifier(randomstate=0)
tree_1.fit(Xtrain,ytrain)
#正答率の出力
print('train acc: %.3f' % tree_1.score(Xtrain, ytrain))
print('test acc: %.3f' % tree_1.score(Xtest, ytest))

train acc: 0.976
test acc: 0.872

決定木は過学習を起こしているため、条件分岐を途中で打ち切り、深い枝での条件分岐を抑えてバリアンスを防ぐ剪定を加えます。

from sklearn.tree import DecisionTreeClassifier
tree_1 = DesicionTreeClassifier(randomstate=0,max_depth=8)
tree_1.fit(Xtrain,ytrain)
#精度の確認
print('train acc: %.3f' % lr.score(Xtrain, ytrain))
print('test acc: %.3f' % lr.score(Xtest, ytest))

train acc: 0.910
test acc: 0.891

決定木の深さ（max_depth）は手動で簡易に試したところmax_depth=8の時が過学習を抑え、なおかつ精度が高く出るという結論に至りました。
この場合、ロジスティック回帰より決定木の方がtrainデータ、testデータ共に精度が高くなり、ツリーベースのアルゴリズムを軸に改良を加えることにしました。

ツリーベースのアルゴリズムには一般的に決定木に加え、それほど性能が高くないモデルを複数組み合わせて汎化性能を向上させるアンサンブル学習としてバギング（代表手法：ランダムフォレスト）やブースティング木（代表手法：勾配ブースティング木）が挙げられます。
①ランダムフォレスト
過学習させたそれぞれの決定木の予測ラベルを多数決して最終的な出力を決める。
②勾配ブースティング木
ひとつのモデルの間違いを訂正するようなモデルを逐次的につくることで､高い汎化性能を実現しようとする。

①ランダムフォレスト

#ランダムフォレストによる学習
from sklearn.ensemble import RandomForestClassifier
rfc_1=Randomforestclassifier(random_state=0,n_estimators=12)
rfc_1.fit(X_train,y_train)

#正答率を出力
print('train acc: %.3f' % rfc_1.score(Xtrain, ytrain))
print('test acc: %.3f' % rfc_1.score(Xtest, ytest))

train acc: 0.969
test acc: 0.879

ランダムフォレストで調整すべきパラメータはランダムフォレストに含める決定木の本数（n_estimators）ほどで12本の時が精度が高くなるようでした。

②勾配ブースティング木

#勾配ブースティング木による学習
from sklearn.ensemble import GradientBoostingClassifier
gbct=GradientBoostingClassifier(random_state=0,max_depth=3,learning_rate=0.15)
gbct.fit(Xtrain,ytrain)
#正答率の出力
print('train acc: %.3f' % gbct.score(Xtrain, ytrain))
print('test acc: %.3f' % gbct.score(Xtest, ytest))

train accuracy: 0.909
test accuracy: 0.896

勾配ブースティング木では調整すべきパラメータはいくつかありますが、学習率（learning_rate）を0.15とした場合が過学習を抑えつつ、高い精度が出せました。

以上のようにツリーベースのアルゴリズムを決定木、ランダムフォレスト、勾配ブースティングの3通り試しましたが、分析手法として多く行われている決定木やランダムフォレストより自分の設定したパラメータでは勾配ブースティングで精度が最も高く出ました。

#6 改良
ここからは勾配ブースティング木をベースに精度の向上を目指します。
●カラムの増減
説明変数にeducationとloanも加えます。

#ランダムフォレストの正答率
train acc: 0.980
test acc: 0.876
#勾配ブースティング木の正答率
train acc: 0.909
test acc: 0.898

説明変数を増やすという観点から、既存の説明変数を利用する手段に加え、説明変数を新しく作ってみました。
campaign（現キャンペーンにおける接触回数）とprevious（接触実績）を足し合わせたtotal（総接触実績）というカラムを作っていたQiita記事を見つけたので模倣を試みました。

train['total']=train['previous']+train['campaign']
#相関係数の出力
np.corrcoef(train['total'], train['y'], rowvar=True)

#array([[ 1.        , -0.00713106],
       [-0.00713106,  1.        ]])

相関はあまり見られず著しい精度の向上には繋がらないと判断しました。

●チューニング
先ほどのランダムフォレストと勾配ブースティング木ではパラメータは手動で設定しましたが、分類問題には回帰問題以上に多様な評価指標が存在し、最適なハイパーパラメータを定めることが重要であり、手動では限界があります。
今回はグリッドサーチを交差検証法を用いて行い、ハイパーパラメータの最適な値を探索的に定め、汎化性能が最も高くなる組み合わせを探します。

①ランダムフォレスト
今回検証するパラメータは以下の4つです。

名称	説明
n_estimators	決定木の本数
max_features	各決定木で分類に使用する説明変数の数
max_depth	各決定木の深さ
min_samples_leaf	決定木の葉に分類されるサンプル数

#調整したいパラメータを指定
param_grid={'n_estimators':[60,80,100,120],
            'max_features':[1,None,'auto'],#auto:全ての説明変数の平方根
            'min_samples_leaf':[3,4,5,6],
            'max_depth':[1,3,5,8,10]}

gcv = GridSearchCV(RFC(),param_grid,cv=5)
gcv.fit(Xrain,ytrain)

#最適なパラメータを表示
gcv.best_params_
#{'max_depth': 10,
 'max_features': 'auto',
 'min_samples_leaf': 6,
 'n_estimators': 120}

上の出力の通りパラメータを設定してランダムフォレストで実行すると以下のような結果を得られました。
train acc: 0.918
test acc: 0.899
先ほどよりtrainデータの精度が4%、testデータの精度が4%上がり成果が見られました。

②勾配ブースティング木
今回検証するパラメータは以下の4つです。

名称	説明
n_estimators	決定木の本数
learning_rate	学習率
max_depth	各決定木の深さ
min_samples_leaf	決定木の葉に分類されるサンプル数

#調整したいパラメータを指定
param_grid={'n_estimators':[60,80,100,120],
            'learning_rate':[0.05,0.1,0.15,0.2],
            'min_samples_leaf':[3,4,5,6],
            'max_depth':[1,3,5,8,10]}

gcv2 = GridSearchCV(GBC(),param_grid,cv=5)
gcv2.fit(Xtrain,train)


#最適なパラメータを表示
gcv2.best_params_
#{'learning_rate': 0.05,
 'max_depth': 5,
 'min_samples_leaf': 5,
 'n_estimators': 100}

上の出力の通りパラメータを設定して勾配ブースティング木で実行すると以下のような結果を得られました。
train acc: 0.915
test acc: 0.895
trainデータでの精度は上がったもののtestデータの精度はあまり変化しませんでした。

今回のグリッドサーチによるパラメータの設定の結果、勾配ブースティング木よりランダムフォレストの方が僅かながら高い精度が出ました。よって最終的にはランダムフォレストを用いることにしました。

#7 結果・反省
このような前処理や改良の下、結果としてランダムフォレストで実行すると0.89716の成果を得ました。
なお前処理で数値データのカテゴリ分けやグリッドサーチを行わずに勾配ブースティング木で実行した際は0.88125で824/1436位だったので少し精度が改善できたことになります。
反省として試してみたい手法や前処理の工夫を挙げます。

①手法選択
今回は最初の回帰アルゴリズムと分類アルゴリズムのどちらを用いるかの選択として、ロジスティック回帰を用いましたが、非線形の分離に対応可能でパーセプトロンやロジスティック回帰より表現力が高いとされるSVMを用いた場合、今回用いたロジスティック回帰、決定木、ランダムフォレスト、勾配ブースティング木よりも良い精度が出せた可能性があります。

②データの前処理
今回、数値データである年齢と最終接触月を口座開設率の高いグループと低いグループに分類した場合、相関が見られ精度の向上に繋がりました。
同様に職種や最終接触時間に関してもグループ分けした場合、職種であれば事務職、技術職などのカテゴリに分けると何らかの相関が見られる可能性があり、最終接触時間は長い方が今回も話を聞いてくれ口座開設に至る傾向を予測でき、データを加工することで高い精度が出せる可能性があります。

③改良
今回、グリッドサーチによって最適なハイパーパラメータを探索的に求めましたが、ランダムフォレストでは著しい精度の改善が見られましたが、勾配ブースティング木では思わしい結果を得られませんでした。その理由として、設定したハイパーパラメータがどれが適切なものであるか理解が不足していたことにあると思います。適切なものがどれか他のコンペのQiita記事なども参考にしながら勉強していきたいと思います。

以上のようにまだまだ改善の余地は多いため、時間があれば今後取り組んでみたいと思います。