#さっそく初めていきたいと思います。
pythonのsklearn.datasetsの中には学習に適したデータセットが公開されています。
こちらで詳しくコードを書いて説明をしていきます。
実際に手を動かす前に各変数の説明を載せておきます。
| 列名 | 説明 |
|---|---|
| CRIM | 町ごとの一人あたりの犯罪率 |
| ZN | 宅地の比率が25,000平方フィートを超える敷地に区画されている。 |
| INDUS | 小売業の商業が占める面積の割合 |
| CHAS | チャールズ川沿いかどうか。1→川の周辺 0→それ以外 |
| NOX | 窒素酸化物の濃度 |
| RM | 住居の平均部屋数 |
| AGE | 1940年より前に建てられた持ち主が住んでいる物件の割合 |
| DIS | 5つのボストン雇用施設からの重み付き距離 |
| RAD | ラジアルハイウェイへのアクセス可能性の指標 |
| TAX | 10,000ドルあたりの税額固定資産税率 |
| PTRATIO | 生徒教師の比率 |
| B | 街における黒人の割合 |
| LSTAT | 人口あたり地位が低い割合 |
まず必要なライブラリを取り込んでいきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
さっそくデータセットを取り込んでいきます。
カラムにはデータセットのカラムをそのまま使おうと思います。
from sklearn.datasets import load_boston
dataset = load_boston()
x, t = dataset.data, dataset.target
columns = dataset.feature_names
次にデータセットの確認をしていきましょう。
type(x), x.shape, type(t), t.shape
(numpy.ndarray, (506, 13), numpy.ndarray, (506,))
データはNumPyのndarray型で格納されていることが確認できました。
また、x とt にはそれぞれ「506行13列」と「506行1列」が格納されていることがわかるでしょうか。
格納されている型をDataFrame型に変換しましょう。
df = pd.DataFrame(x, columns=columns)
df.head(3)
out
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 |
そしてdfにTargetというカラムを追加します。
df['Target'] = t
df.head(3)
out
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | Target |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
Targetというカラムが追加されたのが確認できますでしょうか。
それではデータを分割するフェーズに移りたいと思います。
なぜこのようなことをするのかというと、過学習を防ぐためです。
例えば練習では高い精度で分析できても本番でそれが発揮できなきゃ意味がありません。
このような機能を汎化性能といいます。
これは機械学習の大きな課題ですので覚えておいて損はないワードです。
from sklearn.model_selection import train_test_split
ここで関数が登場します。
sklearn.model/selection.train_test_split()
です。
以下ではxをx_train, x_test、tをt_train, t_testに分割しています。
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
ここではモデルをインポートしています。
次の行ではインスタンスが生成されています。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
モデルの学習をしています。
ここで入力値にx_train、目標値にt_trainが使用されていることに注目してください。
model.fit(x_train, t_train)
出力結果です。
LinearRegression()
重回帰分析では重みをw、バイアスをbとして表現していました。
ここで求まったwの値はmodel.coef_に。
バイアスbの値はmodel.intercept_に格納されています。
結果を見ていきます。
model.coef_
学習後のwを見ていきましょう。
model.coef_
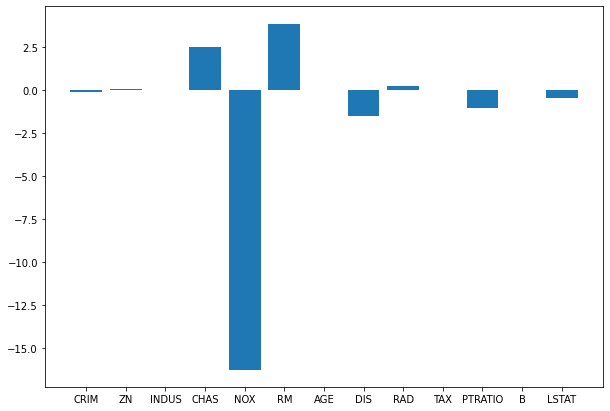
array([-1.21310401e-01, 4.44664254e-02, 1.13416945e-02, 2.51124642e+00,
-1.62312529e+01, 3.85906801e+00, -9.98516565e-03, -1.50026956e+00,
2.42143466e-01, -1.10716124e-02, -1.01775264e+00, 6.81446545e-03,
-4.86738066e-01])
可読性を上げるためにヒストグラムにしてみます。
plt.figure(figsize=(10, 7))
plt.bar(x=columns, height=model.coef_)
次に学習後のbを見ていきます。
model.intercept_
37.93710774183309
次に計算して求まった決定係数を見ていきましょう。
とりあえずは1に近いほど高精度という認識で良いでしょう。
print('train score: ', model.score(x_train, t_train))
print('test score: ', model.score(x_test, t_test))
学習済みモデルを用いて学習用データセットで計算してみた結果(train score)はおおよそ0.76になりました。
また、テスト用データセット(test score)はおおよそ0.67という結果を示しました。
ここではtrain scoreがより大きい値を示していることがわかり、予測値と目標値に大きな差異が生まれていることがわかります。
これを過学習といいます。
train score: 0.7645451026942549
test score: 0.6733825506400171
ここまでお疲れさまでした。
次で最後の操作となります。
最後に新たな入力値を与えて推論を行ってみましょう。
y = model.predict(x_test)
predict()メソッドにテスト用データセットからサンプルをひとつ取り出してみましょう。
print('予測値: ', y[0])
print('目標値: ', t_test[0])
ここでもわずかに予測値が目標値を上回っていることがわかりました。
予測値: 24.935707898576915
目標値: 22.6