本稿では原因結果グラフで全称命題と存在命題を扱うために量化子を導入する方法を提案します。
誤りや、より良い方法があれば教えていただけると幸いです。
二項分類と多項分類
ある要素の分類方法には二項分類と多項分類があります。1
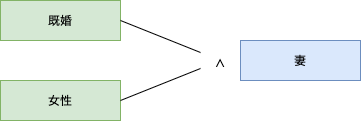
二項分類はその因子の条件を満たすかどうかという二値の分類で、水準を省略可能です。
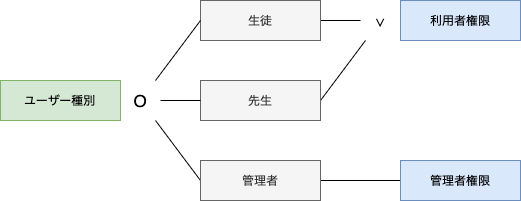
多項分類の場合は因子に対して同値分割を用いて水準を定義し、制約記号で因子と水準の包含関係を明確にします。
全称命題と存在命題
さて、前述の二項分類・多項分類は単一の要素がどの条件を満たすかという問題であるのに対して、次の全称命題・存在命題では条件を満たす要素がどれだけ存在するかという問題を扱います。
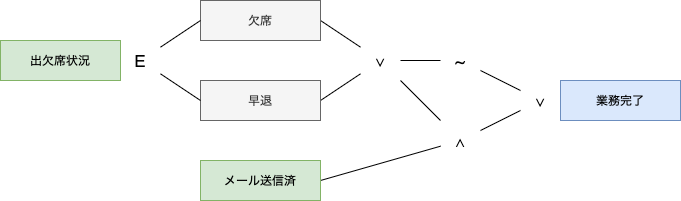
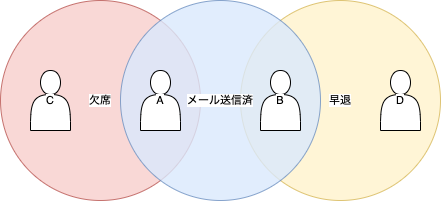
(例) ある塾では欠席または早退した生徒全員に授業のフォローメールを送信するという業務がある。
これを原因結果グラフで表現すると下図のように考えられそうです。
しかし、メールは送信したけど一部の人に送信し忘れていた場合はどうでしょうか?
もしくは、メールは送信したけど別の人に送信してしまった場合は?
この原因結果グラフからは正しい結果を読み取ることができません。
なぜなら、「欠席者」も「早退者」も「メール送信済の生徒」も集合だからです。
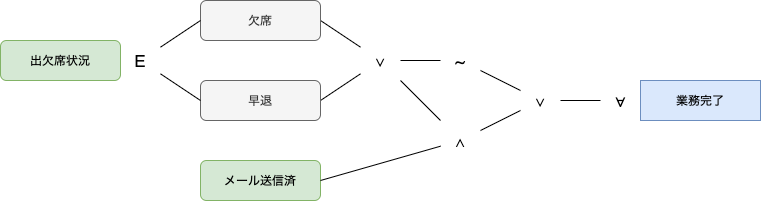
そこで、リンクを拡張して量化子を導入すると、下図のように書けます。
通常の命題と区別するため、因子を角丸にしました。
上図より、生徒の集合をXとすると業務完了する条件は「∀ x ∈ X, ¬ (欠席 ∨ 早退) ∨ ((欠席 ∨ 早退) ∧ メール送信済)」となります。
このとき因子は命題ではなく、命題関数となっている点に注意してください。
例えば、「xは欠席である」という文章は変数xが確定するまで真偽を評価できません。
命題関数に接続された論理演算は次のように遅延評価されます。
ケース: 授業の参加者が出席者2人のみの場合
量化子に辿り着いたら左に折り返して値が確定していきます。
①: 「欠席、または早退である」
②: ①の否定
③: { 出席者, 出席者 } という集合の全ての元に対して、②が成り立つ
②': { 出席者, 出席者 } という集合の全ての元に対して、①の否定が成り立つ
①': { 出席者, 出席者 } という集合の全ての元に対して、「欠席でない、かつ早退でない」が成り立つ
∴ 授業の参加者が出席者2人のみの場合、業務完了は真である。
テストケースの作成
先ほどの原因結果グラフを元にデシジョンテーブルを使ってテストケースを作成する方法を考えます。
総当たりで8通りの組み合わせができますが、制約条件より「早退 ∧ 欠席」を満たすケースはあり得ないので削除します。
そうすると、下図のように6通りの組み合わせが残ります。
例えば、1のテストケースは早退かつメール送信済の生徒を対象にしたテストです。
それ以外の条件が混ざってしまうと意味のあるテストにならないので、「∀ x ∈ X, ¬ 欠席 ∧ 早退 ∧ メール送信済」を満たすテストケースを作成します。
※「欠席の生徒が存在しない ∧ 早退の生徒が存在する ∧ メール送信済の生徒が存在する」ではないので注意してください。
これで有則の組み合わせを全て網羅することができましたが、下図のように複数の条件が混在するケースに不具合が潜んでいる可能性もあります。
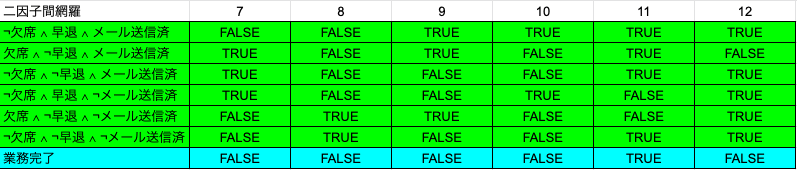
今回はこのようなケースは無則の組み合わせと見なし、Pictを使って二因子間網羅のテストケースを作成してみました。
例えば、7のテストケースでは早退かつメール未送信の生徒が存在するので、業務完了が偽です。
先ほどの全網羅のテーブルとは異なり、こちらは各行の条件を満たす生徒が存在するかという意味で書いています。
以上です。
-
これは統計学の用語で、ソフトウェアテストの一般的な用語ではありません。 ↩