はじめに
アプリ開発エンジニアとして長く生きてますが、このところ旬な領域とか手を出してみようかなー、数学のお勉強しなきゃかなー、とか思ってみたりしたときに。
ふと気づいたのですよ。
私、もともと受験科目に数学があったし、なんならそのへん大学でやったはず。人工知能とか、パターン認識とか。すっっっっかり忘れてるけど。
というわけで、色々手元に残ってたテキスト類からまずこちらを引っ張り出してみました。

数値計算プログラミング
初版1986年5月。数値計算プログラミングってググると、33年も経っていまだヒットする本。あんまりこの手の本てないんですね。
とりあえず、復習がてらこの本に載ってるコードをCとPythonに移植してみます。
全部で32個載ってますが、のんびりやっていこうと思います。
このあと、出てくるコードはMacのVisual Studio Codeで書いてます。FortranとCはgcc使ってコンパイルしてます。
計算機イプシロンの生成
丸め誤差
1章P.4〜5の要約。
プログラム中の数値は基本的に切り捨てまたは丸められる。その切り捨てあるいは丸めによって生じる誤差を、丸め誤差という。
β進n桁の浮動小数点に切り捨てを行ったときに生じる相対誤差の上限は、
\frac{\beta^{-n}}{\beta^{-1}} = \beta^{-(n-1)}
この1に相対的な最大丸め誤差
\epsilon_M = \beta^{-(n-1)}
は使用する浮動小数点体系に特有の値で、**計算機イプシロン(machine epsilon)**という。
この値は、
1\oplus\epsilon_M> 1 \tag{1}
を満足する最小の正の浮動小数点数として定義することも出来る。 $\oplus$ は加算を行ったあとに切り捨てあるいは丸めの操作を行うことを意味する。
Fortranのコード
(1)の定義に基づくFortranプログラム。
SUBROUTINE MACEPS(EPSMAC)
EPSMAC = 1.0
100 CONTINUE
IF (1.0 + EPSMAC .LE. 1.0) THEN
EPSMAC = 2 * EPSMAC
RETURN
END IF
EPSMAC = EPSMAC * 0.5
GO TO 100
END
program maceps_main
call maceps(epsmac)
write(*,*)epsmac
end program maceps_main
本に載っているコードはサブルーチン部分だけだったので、メイン部分(下4行)は追加。小文字は私が追加したコード、大文字が本のまま、と書き分けます(Fortranは大文字小文字を区別しません)。
実行結果は
1.19209290E-07
になります。
コードの理解
いきなり最初のコードからGO TO文ですよ。いや、仕方ない。著者(故人)は数値解析学の偉い先生であってエンジニアではない。
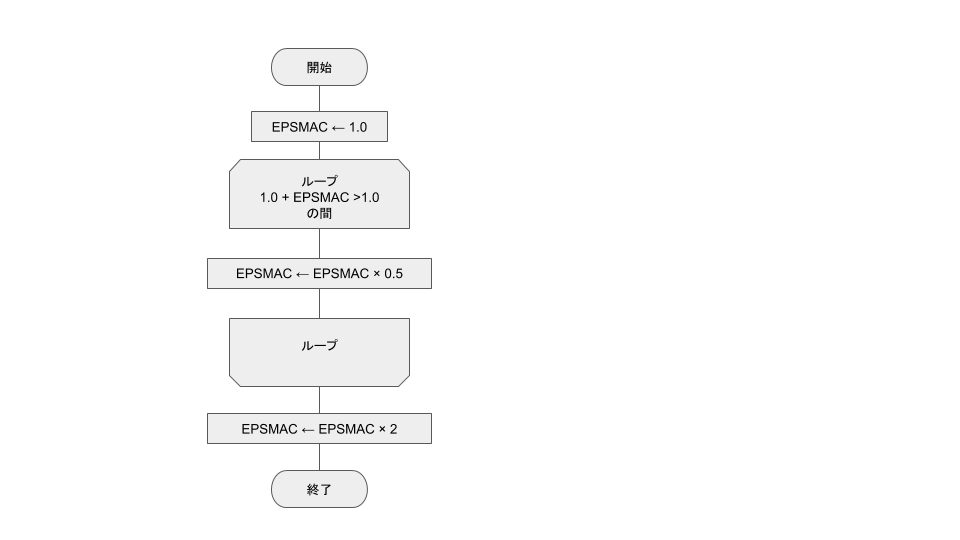
とりあえず、フローチャートに起こしてみます。
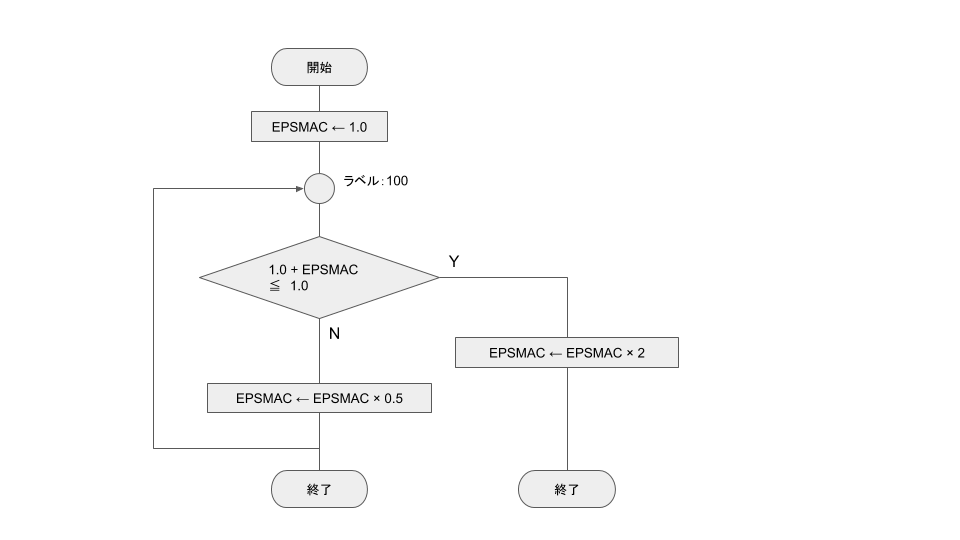
うん。とりあえず、新人がこんな流れを持ってきたら暴れます。
- 構造化しろ
- 必然性もないのにモジュールの途中でモジュール抜けるな
JIS流れ図の基本では、ループの条件は終了条件ですが、これから移植するCとPythonはループ条件は継続条件なのでその形で。
Cのコード
# include <stdio.h>
# include <float.h>
void maceps(float *epsmac){
*epsmac = 1.0f;
while((1.0f + *epsmac) > 1.0f)
{
*epsmac *= 0.5;
}
*epsmac *=2;
}
int main(void){
float epsmac;
maceps(&epsmac);
printf("%.8E\n", epsmac);
printf("%.8E\n", FLT_EPSILON);
return 0;
}
Fortranのコードが単精度浮動小数点なので、Cでもfloat使います。
基本Fortranのコードに合わせたかったので、メインからポインタで変数渡してメインで表示。
で、Cではfloat.hで計算機イプシロンが定数で定義されているので、メインではそちら(FLT_EPSILON)も表示してみました。
実行結果は
1.19209290E-07
1.19209290E-07
になります。
Pythonのコード
import numpy as np
def maceps(epsmac):
epsmac[0] = 1.0
epsmac[1] = 1.0
while epsmac[1]+epsmac[0] > epsmac[1]:
epsmac[0] = epsmac[0] * 0.5
epsmac[0] = epsmac[0] * 2
return
epsmac = np.array([0,0],dtype=np.float32)
maceps(epsmac)
print("%.8E" % epsmac[0])
print("%.8E" % np.finfo(np.float32).eps)
Python標準の浮動小数点数は倍精度なので、単精度浮動小数点に合わせるのにnumpy使う。
そしてnumpyにもCと同じく計算機イプシロンは定義されているのでそちらも表示。
実行結果は
1.19209290E-07
1.19209290E-07
です。
このコード、@konandoiruasa さんに、「定数との演算があるとfloat64になってしまう」とコメントにてご指摘いただきました。ありがとうございます。対処法まで書いて頂いたのでご参照ください。
まとめ
EPSMACは繰り返しの中で半分に割られていく(=0.5を掛けてる)。
繰り返しの条件に使っている式、
1.0 + EPSMAC > 1.0
これが成り立たなくなるということは、最後に割る前の値がこれを満たす最小の値ということなので、繰り返しをやめて、最後に割ったのを取り消すために2倍する。
それがつまり(1)の式を満たす最小の正の値 = 1より大きい最小の数と1との差 = 計算機イプシロン、ってことですね。