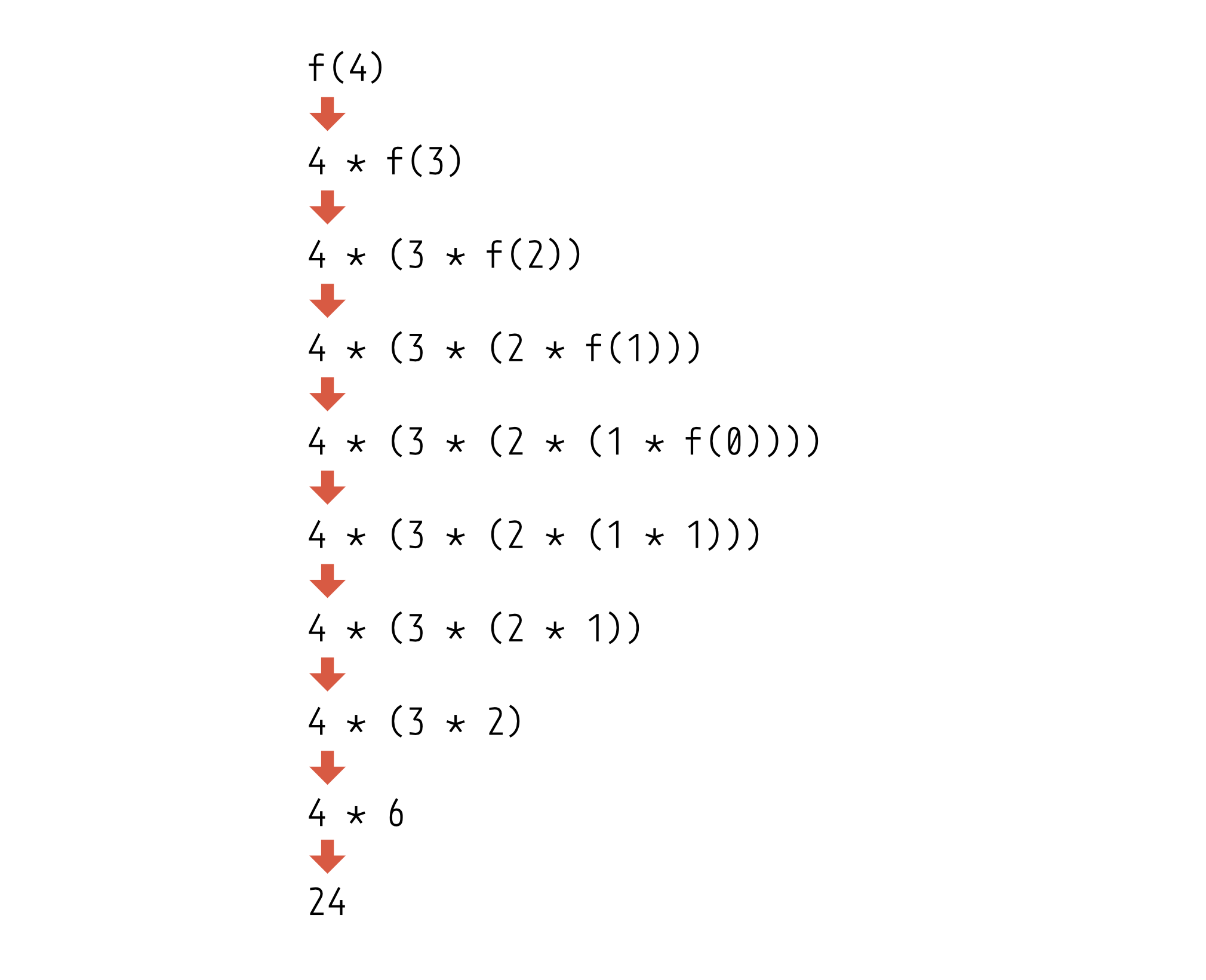必要な知識
JavaScript の基本的な構文、関数、プロパティ、配列
イントロ
例えば「JavaScript で Web ページ上に <a> 要素が何個あるか数えろ」と言われたら、どのようなコードを書くだろうか?もちろん getElementsByTagName() などを使えば簡単だが、それらを使わずに自分で DOM ツリー上を探索して数えるアルゴリズムを実装するとしたら、どうするだろうか?
DOM ツリーというのがどういうものかわからない人も、構造自体はシンプルなので調べてみてほしい。<div> や <a> といったものは要素といい、要素の中にさらに別の要素(子供要素 / child element)がいくつか含まれたり含まれなかったりする。
このような問題は、再帰関数を使えば簡潔かつ直感的なコードで表現することができる。この記事では JavaScript を用いて説明するが、同じ考え方は他の言語にもそのまま適用できる(JavaScript 特有の話ではない)。
再帰関数とは
再帰関数とは自分自身を呼び出す関数である。何のために自分を呼び出すかというと、計算しようとしている問題を少し小さくして自分を呼び出し、その返り値を使って答えを返すという戦略をとっているからである。
再帰関数は特に関数型言語でよく用いられ、中には for 文が存在せず代わりに再帰関数で反復を実現する、という言語も存在する(Haskell や Scheme など)。for 文では変数の値が増え続ける(or 減り続ける)ため、変数の値が変わることを嫌う関数型言語では使われないのである。
定義こそシンプルだが、これだけではイメージを掴むのは難しいので、例を見てみよう。
例: 階乗
factorial (階乗)を計算することを考えよう。「1 * 2 * 3 * ... * n」 を n の階乗という。
多くの人はこれを for 文で実装するだろう。例えばこのように。
function factorial(n) {
let product = 1
for (let i = 1; i <= n; i++) {
product *= i
}
return product
}
ここで、再帰関数のところで述べた通り、問題を少し小さくしてその答えを使って元の問題の答えを計算することを考えよう。
10 の階乗は 1 * 2 * 3 * ... * 9 * 10 である。これを (1 * 2 * 3 * ... * 9) * 10 と分けると、(9 の階乗) * 10 になっていることが分かる。これを一般化すると、(n の階乗) = (n-1 の階乗) * n である。ただし、n = 0 のときは成り立たないので特別なケースとして扱う必要がある(-1 の階乗は定義されていないので)。以上から、階乗は次のように表現することができるということが分かる。
\mathit{fact}(n) = \begin{cases}
1 &\quad (n = 0) \\
n \cdot \mathit{fact}(n-1) &\quad (n > 0) \\
\end{cases}
「n の階乗」が「n - 1 の階乗」で表現されているわけだが、このように前の値で次の値を表現した式を漸化式という。
この漸化式を、そのままコードで書いてみよう。
function factorial(n) {
if (n <= 0) {
return 1
}
return n * factorial(n - 1)
}
なんと、これで再帰関数の完成である。実際に実行してみるとちゃんと正しく計算されることがわかるだろう。factorial(4) の実行過程を図で表すと次のようになる。
しかし、先程このコードを書いたときこのような実行プロセスを考える必要はなかった。漸化式をそのまま書くだけで、正しく動く再帰関数が完成するのである。
繰り返すと、これは**「n の階乗」という問題を「n-1 の階乗」というより小さい問題の答えから計算している。このようにある問題を「より小さい問題の答え」から計算する**というのが再帰関数の本質である。
再帰関数 は stateless なコードで書ける
stateless とは「state (=状態) がない」という意味で、ここでいう状態とは時間とともに上書きされていくデータである。逆に stateful は状態を持つという意味である。
先程の for 文を使ったコードを見てみると、当然だが i と product いう変数の値が時間とともに変わっていっている。よってこのコードは stateful である。
function factorial(n) {
let product = 1
for (let i = 1; i <= n; i++) {
product *= i
}
return product
}
一方で、再帰関数の方は、どの変数も値が変わることがない、stateless なコードである。
function factorial(n) {
if (n <= 0) {
return 1
}
return n * factorial(n - 1)
}
stateful なコードはバグを生みやすい。ある変数の値を複数の場所から共有しているときに、その変数の値を変更するといろいろな場所に影響が出てしまうからである。stateless にすることでこの問題は解決し、さらに並列化しやすいというメリットもある。実際、硬派な関数型言語では、再帰関数を駆使することで徹底的に stateful なプログラムを回避するのである。
再帰関数はツリーの処理にピッタリ!
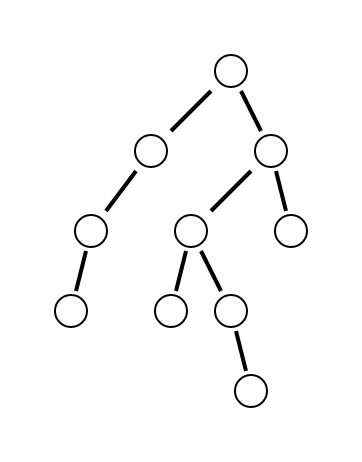
ツリーとは簡単に言うと下に行くほど枝状に広がっていく階層構造である。根と呼ばれるノード(下の図の一番上の○)から始まって、その子供がいくつかあり、それらがまた子供をいくつか持っており...という構造になっている。例としては、ファイルシステム(ファイルとフォルダー)、JSON、そして冒頭に述べた DOM ツリーがある。
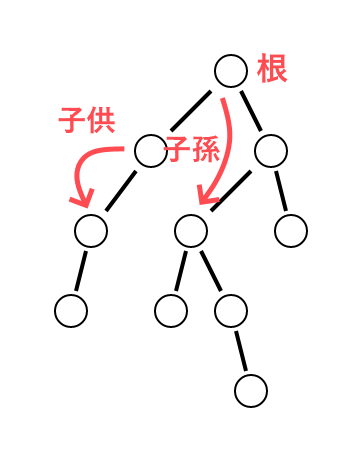
あるノードから見てそれから直接下につながっているノードを**子供(child)といい、子供&子供の子供&そのまた子供...をすべて子孫(descendant)**という。
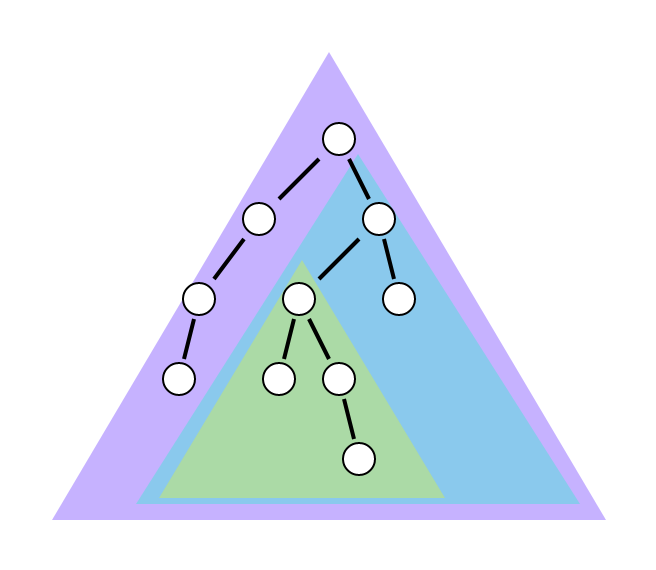
重要なのは、「ツリーの根の子供を見るとまたそれもツリーである」ということである。このように、ある構造が自分と同じ構造を内包している、入れ子状になっているものを再帰的構造という。また「再帰」という言葉が出てきたが、つまりは再帰関数と非常に関わりが深い概念だということである。
例: DOM ツリー
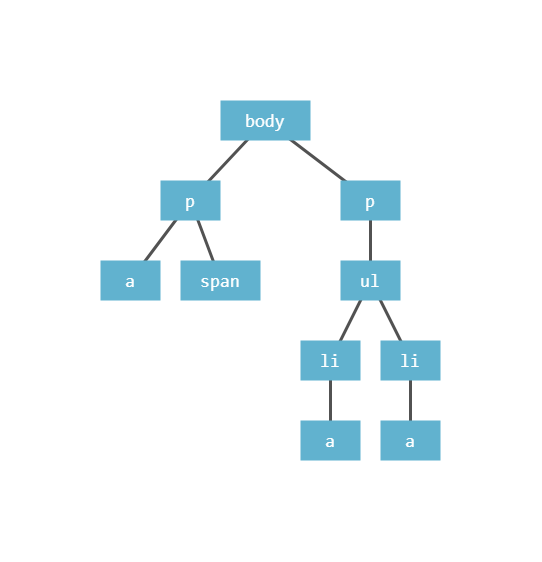
さて、ここで冒頭の問題「DOM ツリー上で <a> 要素 の個数を数えろ」を考えてみよう。Web ページは DOM ツリー(HTML は DOM ツリーの文字列表現と言える)と呼ばれるもので構成されており、通常 <html> 要素が根(一番上のノード) でその子孫としていろいろな要素が含まれている。ただし <a> 要素は <body> 要素の子孫にしか存在しないので、<body> を根として考えることにする。例として下のような DOM ツリーを考えよう。
この問題を解くのに必要な DOM API は次の2つだけである。e は DOM 要素であるとする。
-
e.children=eの子供要素の配列(のようなもの) -
e.tagName=eのタグ名 (<div>要素ならDIV)
さて、先程と同じように、再帰関数を用いて解くことを考えよう。そのためには「少し小さくした問題の答えからもとの問題の答えを計算する」必要がある。ツリーの子供はまたツリーである(再帰的構造)ことから、「あるツリー内の <a> 要素の個数」を「その子供のツリーに含まれる <a> 要素の個数」から計算するのがキレイである。
この再帰関数を countA(e) としよう(引数 e は根である要素)。まず、根 e が <a>要素であるかをチェックする必要がある。<a> 要素 ならば1個、そうでないならば0個である。
次に、子供の要素について考えると、「1つ目の子供の要素とそれより下にある要素」は当然 countA(e.children[0]) である。他の子供についても countA を実行して足し合わせれば、求めたい全体の個数が得られる。
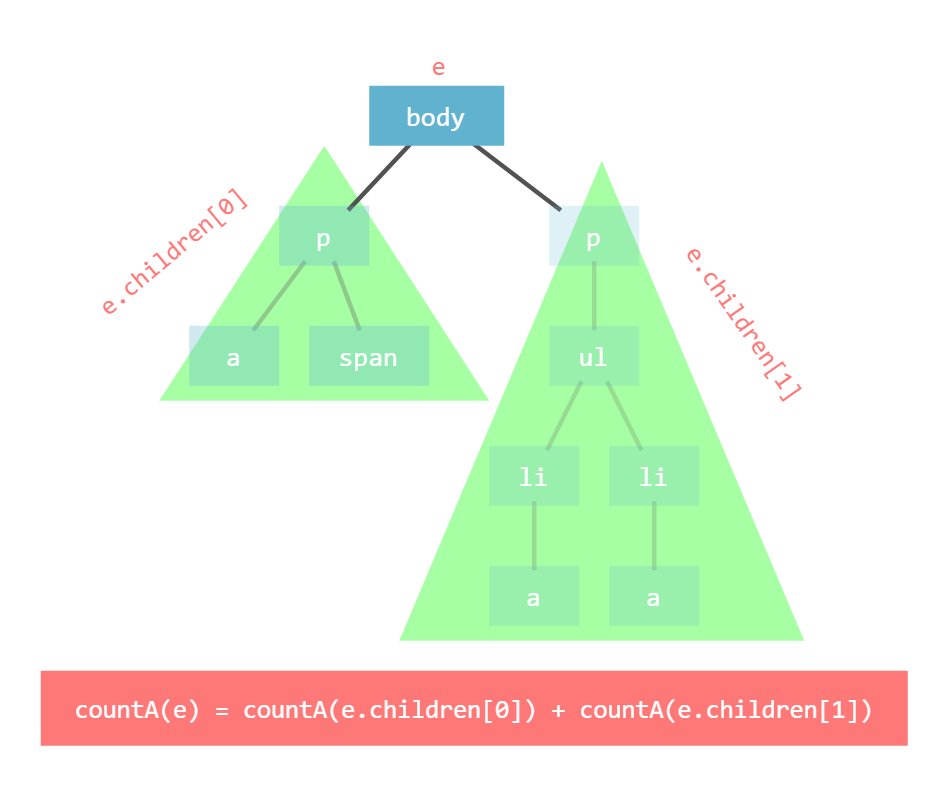
例えば e が <body> 要素ならば下の図のように子要素2つに対して countA を呼び出した結果を足し合わせれば求めたい答えとなる。
以上を踏まえると、次の漸化式が成り立つことが分かるだろう。ただし n は e.children の長さである。
\mathit{countA}(e) = \begin{cases}
\mathit{countA}(\texttt{e.children[0]})+\mathit{countA}(\texttt{e.children[1]})+\cdots+\mathit{countA}(\texttt{e.children[n-1]}) &\quad (e\text{ が a 要素でない})\\
1 + \mathit{countA}(\texttt{e.children[0]})+\mathit{countA}(\texttt{e.children[1]})+\cdots+\mathit{countA}(\texttt{e.children[n-1]}) &\quad (e\text{ が a 要素})
\end{cases}
あとは、これをそのままコードにすれば良い。
function countA(e) {
let count = 0
// e が <a> 要素なら 1 足す
if (e.tagName === "A") {
count += 1
}
// 子供要素に対して再帰的にカウントし和を計算
for (const child of e.children) {
count += countA(child)
}
return count
}
このコードは count 変数などが statelful である。これを完全に stateless にすると次のようになる。.map や .reduce については筆者の別記事を参照されたい。
function countA(e) {
const root = e.tagName === "A" ? 1 : 0
const descendants = Array.from(e.children)
.map(c => countA(c))
.reduce((x, y) => x + y, 0)
return root + descendants
}
以下のデモで正しくカウントできていることが確認できる。
See the Pen recursion on dom tree by righteous (@righteous_github) on CodePen.
なお、この問題は再帰関数を使わずに以下のように while 文でも実装することができる。stack が処理予定の要素を溜めておくための配列で、要素を処理するときその子供を stack に追加する。このようにすることでツリー上のすべての要素を処理することができる。しかし、count や stack が stateful なデータであり、少なくとも筆者にとっては再帰関数の方が読みやすい。
function countA(e) {
let count = 0
const stack = [e]
while (stack.length > 0) {
const el = stack.pop()
if (el.tagName === "A") {
count += 1
}
stack.push(...el.children)
}
return count
}
また、これはスタックを使ってツリーを巡回しているが、再帰関数の方は代わりにコールスタックを使っている、と見ることもできる。
再帰関数のデメリット
再帰関数は、再帰関数を使わない場合の for や while ループの回数分だけ関数呼び出しが発生するため、for や while と比較するとパフォーマンスは悪い(関数は呼び出すために少しのメモリと時間を要する)。また、言語やランタイムによっては、再帰呼び出しが深すぎる(=関数が関数を呼び出し、それがまた関数を呼び出し...というチェーンが長すぎる)とスタックオーバーフローなどのエラーが発生する1。
まとめ
再帰関数は反復処理を stateless なコードで実現するのに不可欠である。パフォーマンスは while や for に劣るが、多くの場合パフォーマンスよりもコードのリーダビリティ(読みやすさ)を優先すべきである。再帰関数は問題の数学的性質(漸化式)を素直に表現することができ、慣れれば非常にリーダブルなコードとなる。また、たとえ再帰関数を使わずとも、問題の再帰的な構造を捉えることはプログラマーとして重要なスキルであると考えられる。この記事でなんとなくでも再帰関数がどのようなものかを理解してもらえれば幸いである。
-
これを回避するために tail call optimization と呼ばれるコンパイラーの最適化手法があるが、この最適化が適用されるためにはある決まった形で再帰関数を書く必要がある。 ↩