強化学習 文献まとめ4
リレー解説 強化学習の最近の発展 第4回
「部分観測マルコフ決定過程と強化学習」
計測と制御 第52巻 第4号 2013年4月号 P374~380
https://www.jstage.jst.go.jp/article/sicejl/52/4/52_374/_article/-char/ja/
をまとめた個人用メモ
※この記事をまとめたのは2021年5月あたりで、強化学習について勉強し始めのときにまとめたもので、間違った内容が含まれている可能性があります
前回:https://qiita.com/he-mo/items/65e0505243934423a966
次回:https://qiita.com/he-mo/items/5899b10fa9046c112903
1. はじめに
部分観測マルコフ決定過程(POMDP,Partially Observable Markov Decision Process)とは、マルコフ決定過程に観測の要素を取り入れたものである。
つまり、状態の全てを完全に観測することができない。意思決定者にとっては全く同じ2つの状況でも、実は異なる状況であり、ある行動を取ると一方では高い利益があるがもう一方では大きな損失が出る。この状況でどの行動を選択すべきかを考えるためには、得られる観測をもとに真の状態について考える必要がある。
部分観測マルコフ決定過程はマルコフ決定過程と比べて問題設定が厳しい。問題を解くにあたっては、事前知識や仮定、要求される性能に応じて手法を選ぶ必要がある。
2. 部分観測マルコフ決定過程
マルコフ決定過程について概要を確認し、部分観測マルコフ決定過程の定義まとめる。
2.1 マルコフ決定過程における強化学習の概要
マルコフ決定過程はの組によって定義される。
Sは状態の集合、Aは行動の集合、Tは状態遷移確率、Rは報酬関数
エージェントは状態に応じて行動選択をして、状態遷移する。その後に報酬を受け取る。これを繰り返し、将来得られる報酬の和が最大になるような方策の獲得を目指す。
2.2 部分観測マルコフ決定過程
部分観測マルコフ決定過程は、 の組として定義される
S,A,T,Rはマルコフ決定過程と同じ
Ωはエージェントの観測の集合、Oは観測を記述する関数
部分観測マルコフ決定過程におけるエージェントは状態を直接観測することができないため、マルコフ決定過程と比較して意思決定が困難である。
エージェントは観測に応じた行動選択をして、状態遷移する。その後に報酬受け取る。これを繰り返して、将来得られる報酬の和が最大になるような方策の獲得を目指す。
3. 解法
解法の分類について述べ、次に部分観測マルコフ決定過程における信念状態について定義する。次に部分観測マルコフ決定過程の学習手法を取り上げる。
3.1 解法の分類
解法の分類をするために分類の言葉を整理し、どのような分類がなされているかを整理する
3.1.1 モデルベースとモデルフリー
モデルベースとは、事前知識の1つとして環境のモデルを用いるもの。その手法による計算を実行するためには、状態遷移確率や観測関数が必要。
モデルフリーとは、環境のモデルを使用しないもの
Q-learningは、環境との相互作用はするものの学習に際して環境のモデル(構成要素である関数)を用いていないのでモデルフリー
3.1.2 オンラインとオフライン
オンラインとは、方策を完全に求められていない学習過程においても、その方策を用いるもの。
オフラインとは、方策を完全に求めてから得られた方策を実行するもの。
3.1.3厳密解、近似解、ヒューリスティクスな方法
厳密解とは、論理通りに正確な解を求める方法。
近似解とは、厳密解を得るのは計算量的に厳しい時に近似によって解を得る方法。
ヒューリスティクスな方法とは、論理的な裏付けは得られていないものの、実証実験によって効果が確認されているもの。
3.2 信念状態
部分観測マルコフ決定過程においては状態として信念状態が用いられる。信念状態とは、どの状態にいるかということを示す確率をならべてつくる「状態」である。
具体例は後ほど
部分観測マルコフ決定過程の具体例を、部分観測マルコフ決定過程の標準的な問題であるTigerを用いて説明する。
Tigerは、2つのドアのどちらを開けるかという問題である。片方のドアを開けると中には虎がいて大きな負の報酬が与えられる。もう片方のドアを開けると正の報酬が与えられる。エージェントはどちらかのドアを開けるという行動以外に、ドアの向こうの音を聞くという行動を取ることができる。つまり、行動は音を聞くlisten、左のドアを開くleft、右のドアを開くrightの3つである
もし通常のマルコフ決定過程なら、この問題は音を聞くことなく自身の状態がわかる。この場合の状態遷移図を以下に示す。
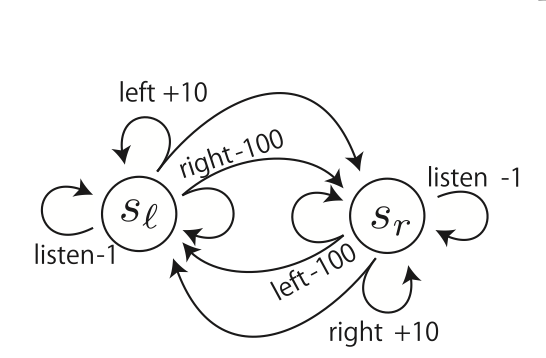
slは左が報酬の状態、srは右が報酬の状態、各行動の数値は報酬を表す。二股に分かれてる矢印は、等間隔でいずれかに遷移することを表す(左が報酬の状態で行動を選択した時、次にどちらに報酬がある状態かは等確率で決まる)
slのときにleft、srの時にrightを選んだ方がいいのは明らかである。
これを部分観測の問題にする。2つの観測xr,xlがあり、音を聞くと85%の確率で正しい状態がわかるとする。これらの状態から、エージェントは自身の状態を推定することとなる。それぞれの状態にいる可能性が等確率であるとき(listenをする前)は、信念状態bは(P(sr),P(sl))=(50%,50%)となる。この状態遷移図を下に示す。
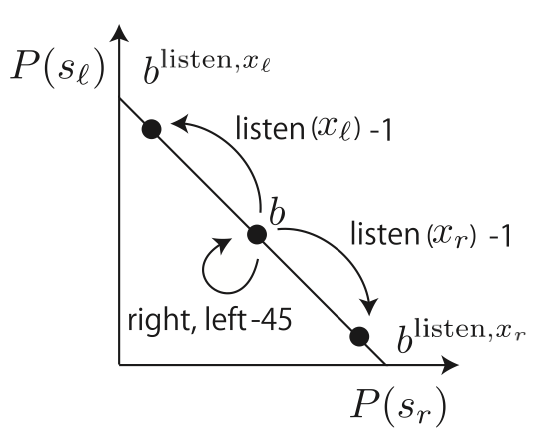
縦軸はslである確率、横軸はsrにいる確率で、この合計は100%である。
真ん中の信念状態bは(50%,50%)の状態で、listenをすることで、信念状態が(85%,15%)または(15%,85%)に遷移する。
listenを行うことで、取らない場合と比べて大きな報酬が得られる(負の報酬が小さく済む)
また、信念状態が(50%,50%)の状態でドアを開けても、状態は変化しない
3.3 モデルベースな手法
この節では、信念状態空間上の価値関数の表現について述べ、価値関数の厳密解を求める手法と近似解を求める手法を説明する。
3.3.1 価値関数の表現
マルコフ決定過程におけるベルマン方程式は以下で表される
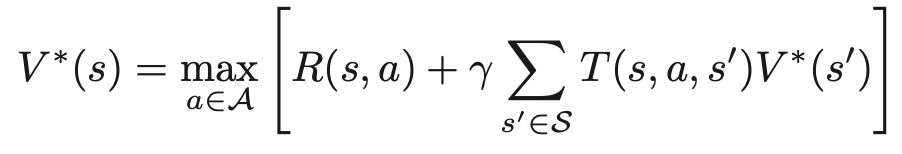
それに対し、部分観測マルコフ決定過程におけるベルマン方程式は以下で表される
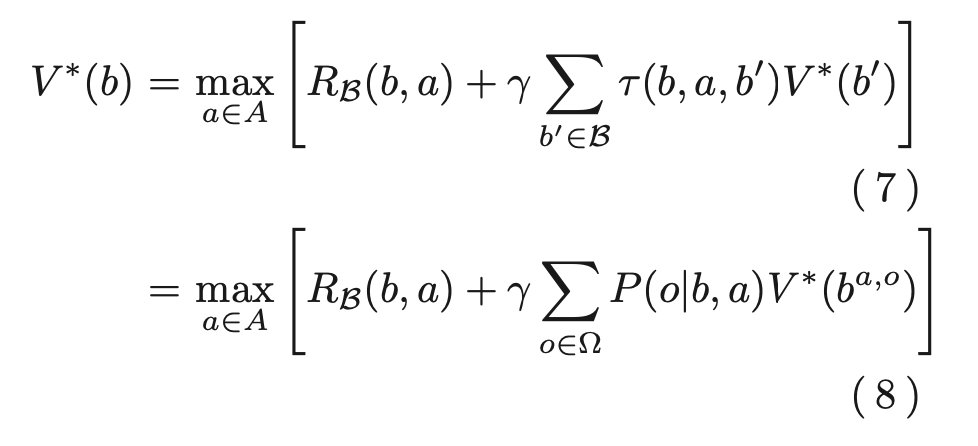
ここでτ(b,a,b′)は状態遷移確率、RB(b,a)は報酬関数で、以下の式によって表される。
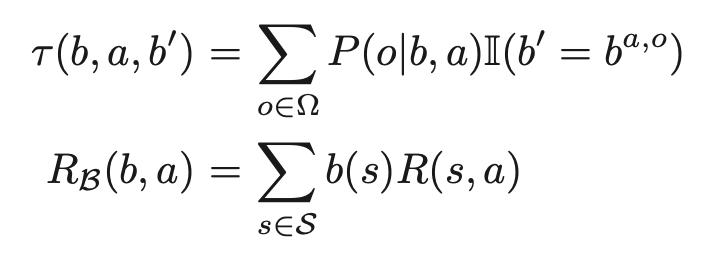
ここで、
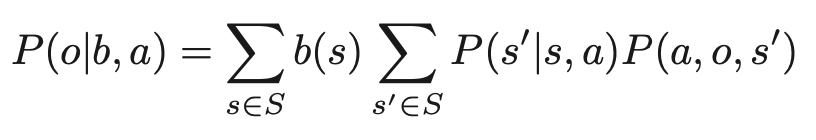
I(b′=ba,o)はb′=ba,oのときに,そのときに限って 1 を返す関数である。
ba,oは、ある信念状態bにいて、行動aをとり、観測oを受けた後の信念状態を表している
ところで、報酬の総和をとる期間が有限か無限期間の一部の場合について次のように表せる
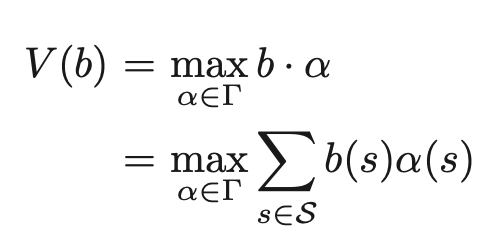
ここでα∈Γ={α1,α2,・・・,αn} はαベクトルと呼ばれるSと同じ次元のベクトルである。
Γは価値関数を表現するαベクトルの集合である。
例えば先ほどのtigerでは、α=rleft=(R(sr , left), R(sl , left))=(-100,10)である。
信念状態b=(0.5,0.5)であれば、αベクトルは価値-45を与える。
3.3.2 Exact value iteration
厳密解を求める手法
式(8)を以下のように分解する
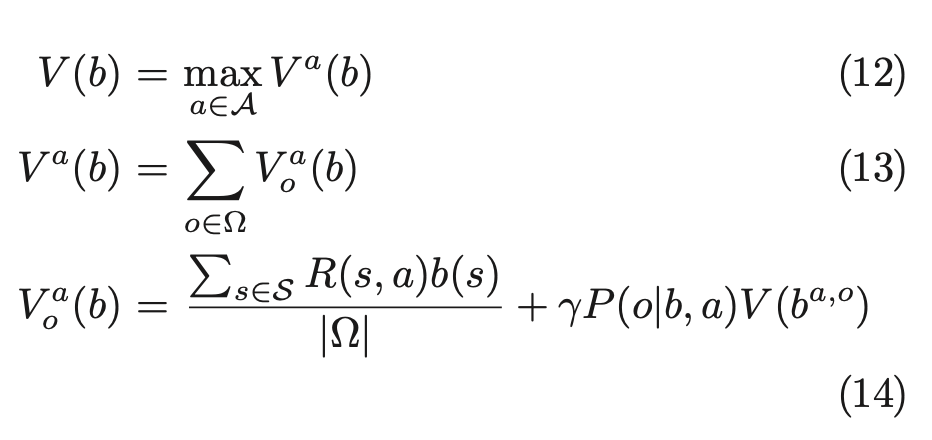
Exact value iterationでは、この式の同様の形式によって以下のように価値関数を更新する
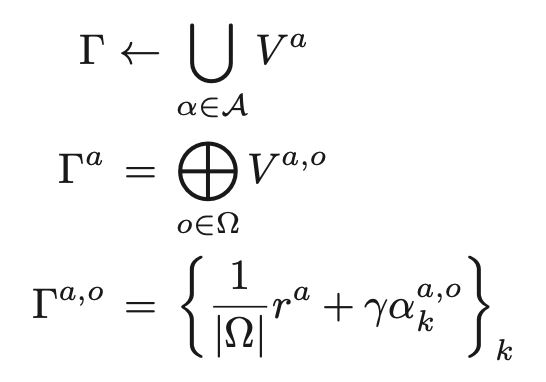
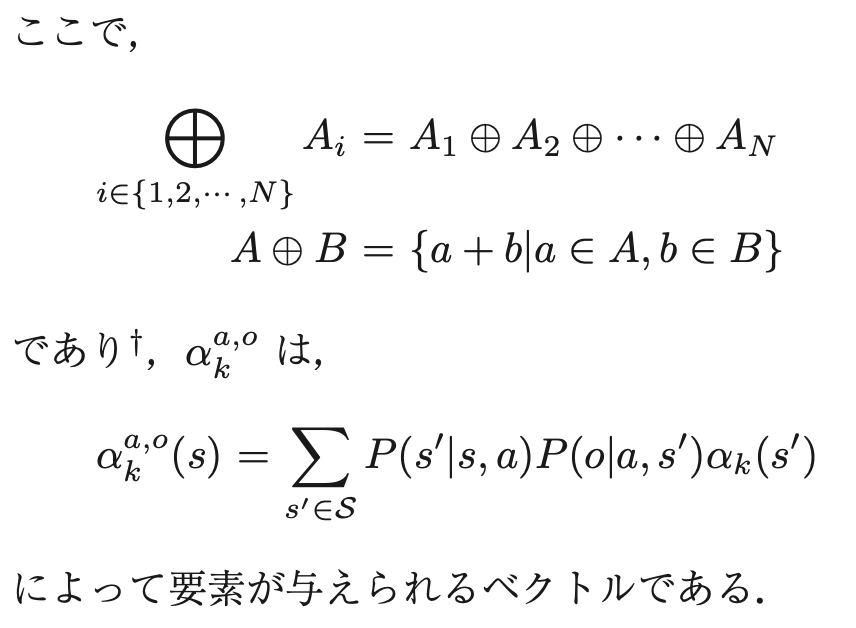
ただし、この方法は計算量が非常に多く、大規模な問題の厳密解を解くことは難しいとされている
3.3.3 Point-based value iteration
厳密解を求めることは計算量的に難しいため、信念状態空間の部分集合Bに対してのみ価値反復を行う手法としてPBVIが提案されている。
3.3.4 Point-based Policy iteration
上記は価値反復法のアルゴリズムであったが、その方策反復法版のやり方としてPoint-based Policy iterationがある。
3.4 モデルフリーな手法
モデルフリーな手法について、アプローチごとに述べる
3.4.1 ブラックボックスなシミュレータを用いる方法
モデルの要素を直接用いる代わりにブラックボックスなシミュレータによってモンテカルロ法を行う手法
POMCPがそれに当たる
状態、観測、報酬などをサンプルする
3.4.2 楽観的価値反復法を用いる方法
適格度トレースを用いたsarsaが部分観測マルコフ決定過程においてよく動作することが実験的に報告されている。
これは楽観的価値反復法に分類される。
適格度トレースとは、TD誤差を複数の状態に責任(≒時間的近さ)に応じて分配。(http://m6chin9h96d.hateblo.jp/entry/2013/11/24/173230 より)
TD誤差=報酬+現在の価値*割引率-直前の価値
ベルマン方程式の「直前の価値」にあたるものを右辺に移行しただけ
3.4.3 価値関数を工夫する方法
信念状態を使わずに部分観測マルコフ決定過程を解くアプローチ
複数のエージェントを切り替えながら行動選択を行うことで、もとの1つの問題をエージェントが学習可能な問題に分割する方法。