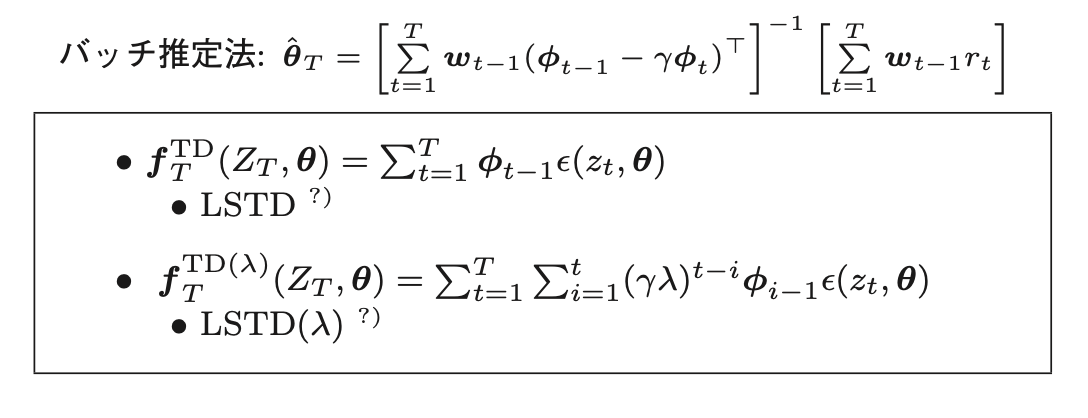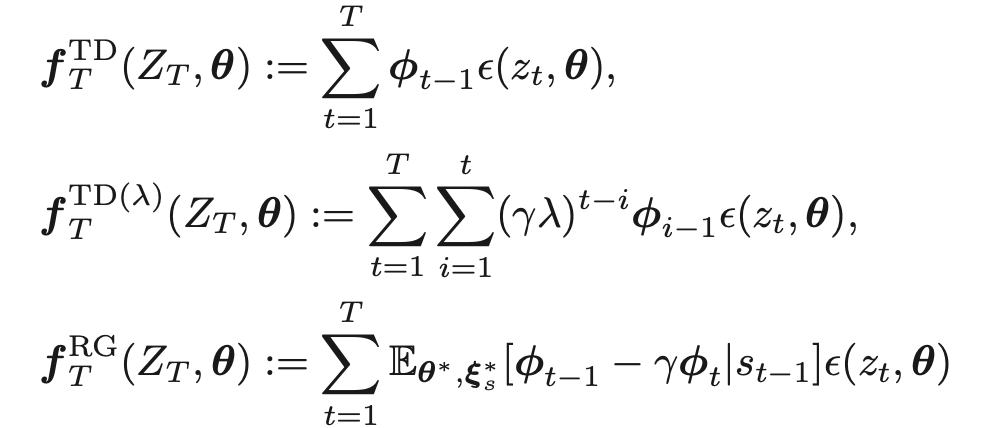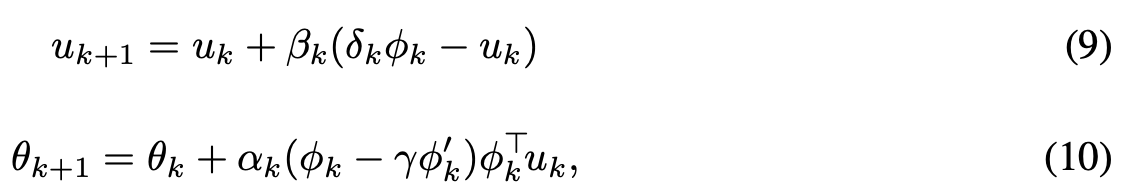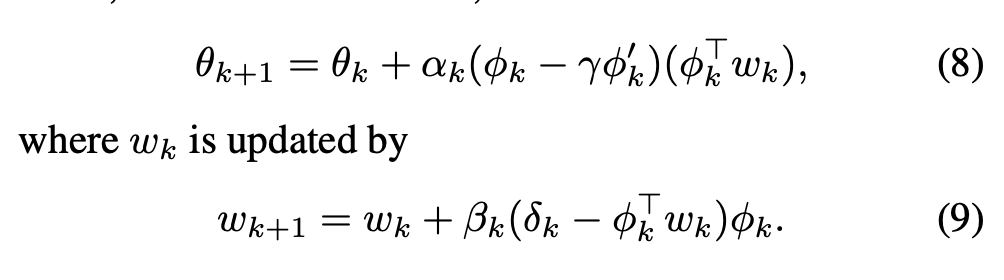強化学習 文献まとめ3
リレー解説 強化学習の最近の発展 第3回
「統計学習の観点から見たTD学習」
計測と制御 第52巻 第3号 2013年4月号 P374~380
植野 剛, 前田 新一, 川鍋 一晃
https://www.jstage.jst.go.jp/article/sicejl/52/3/52_277/_article/-char/ja/
をまとめた個人用メモ
※この記事をまとめたのは2021年5月あたりで、強化学習について勉強し始めのときにまとめたもので、間違った内容が含まれている可能性があります
前回:https://qiita.com/he-mo/items/b1689b6df605936e82d3
次回:https://qiita.com/he-mo/items/c940261bbfec5ce90fdb
はじめに
強化学習(この文献では方策反復法について扱ってる)の方策評価(価値関数の推定)を統計学に基づき議論する
強化学習は、
- 現在までのサンプル系列から価値関数を推定する方策評価
- 価値関数を改善するように方策を更新する方策改善
の2ステップを繰り返して方策の最適化を行う
1つ目の方策評価(価値関数の推定)の精度が強化学習の精度に大きくかかわってくる
方策評価方法はいろいろ提案されているが、どれが優れているかという統一的な議論はなされていない
この文献では、方策評価法を統計学の立場から定式化し、その漸近的な性質について議論した最新の研究をもとに、方策評価に関する理論解析の方法、ならびにそれに基づく解析結果について解説している
//メモ あくまで統計学の立場から行った解析結果を述べるのみで、どれが優れているかの結論は出してない
強化学習は未知の環境における方策評価を求められる
これは興味のない未知の分布、パラメータを含むパラメータ推定問題であるセミパラメトリック推定として定式化できる
セミパラメトリック推定として扱うことで、統計学の解析法を利用でき、これを用いてこれまで提案されてきた価値関数の推定の性質を統一的に評価可能
パラメータ推定ってなんぞや
得られたサンプルから、パラメータを推定する
例えば、正規分布に従う母集団から得られたサンプルを用いて正規分布のパラメータであるμ(平均)とσ(標準偏差)を求めるなど
セミパラメトリック推定ってなんぞや
パラメータに重要なものと重要でないものがあるパラメータ推定
この文献の要点
- 方策評価の問題が、興味のあるパラメータと興味のないパラメータを含む統計モデルであるセミパトリックモデルを通じてセミパトリック統計学習問題として定式化できる
これにより、セミパトリック統計学習問題の強力な解析ツールである推定関数を利用することができる
// メモ 推定関数はパラメータを推定する - 推定関数は、セミパラメトリック統計学習問題において、M-推定量と呼ばれる一致性を持つ推定量(一致推定量)を導く
一致推定量・・・サンプルが多いほど、それから得られる推定結果は母数のそれに近くなる
この推定関数となりうる関数について考察することで、方策評価におけるすべてのM-推定量を包含する一致推定量のクラスを導く
導出した一致推定量のクラスにより、これまでに提案された代表的な方策評価方法の全てを説明できる - 一致推定量のクラスに漸近解析を行うことで、全てのM-推定量の推定精度を評価できる
最高の推定精度を持つ推定量を選択することで、最適なM-推定量を導出できる
マルコフ報酬過程と方策評価
方策を評価したいため、マルコフ報酬過程について扱う
マルコフ報酬過程とは、マルコフ決定過程から行動という要素を取り除いたもの
価値関数(V(s))を推定するにあたり、状態空間Sの次元が大きい場合、各状態sに対応してV(s)を保持するのは現実的でない
なので、価値関数をSより小さい次元のパラメータθで表現し、そのパラメータを調整することで価値関数を計算することを考える。このパラメータθを用いた価値関数をg(s;θ)と表現する
つまり
V(s)=g(s;θ)
ただしθの次元数<Sの次元数
TD学習とLSTD学習
方策評価の基礎となるもの
TD学習
TD誤差は方策評価を考える上で最も重要な役割を担う
TD誤差は下記で定義される
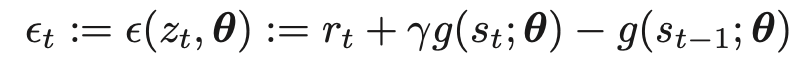
zt={st−1,st,rt}
TD誤差=報酬+現在の価値*割引率-直前の価値
-g(st-1;θ)を左辺に移項すれば、ベルマン方程式になる
TD学習は、TD誤差の期待値が0になるように、更新式に従ってθを更新するオンライン推定方である
θの更新は、学習係数を適切に調整することで真の価値関数を表現できるパラメータθ*に収束するが、一般的にそれは難しい
LSTD学習
TD誤差は逐次更新していくのに対して、LSTDはサンプル系列ZTを同時に用いて、TD誤差の期待値が0になるようにθを一撃で推定する
下記の方程式の解を求めることで実行される
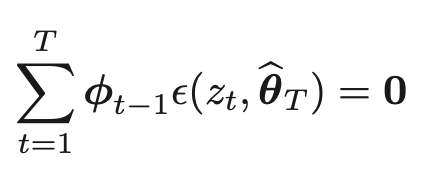
ZT・・・{s0, s1, r1 · · · , sT , rT } のような、時刻Tまでの履歴
TD学習と同様に真のパラメータθ*に収束する
学習係数を必要としないが、計算コストが大きく、サンプルが少なければ数値的な不安定が生じる
要するに
TD、LSTDはパラメータθを求めるもの
セミパラメトリック統計学習に基づく定式化
方策評価のセミパラメトリック統計学習問題としての定式化をする
セミパラメトリックモデル・・・重要なパラメータと重要ではないパラメータを含む統計モデル
セミパラメトリック統計学習・・・重要でないパラメータを知ることなく、知りたいパラメータのみを推定する
証明は省略
方策評価は、セミパラメトリック推定問題と解釈できる
これにより、統計学習で確立されている推定関数による解析ができる
推定関数は、セミパラメトリック統計学習下で重要でないパラメータに依存しない一致推定量を設計する方法を提供する
セミパラメトリックモデルと推定関数
セミパラメトリックモデルと推定関数について説明。マルコフ報酬過程におけるそれは次の節で述べる
セミパラメトリックモデルp(x;θ,ξ)について考える。θは重要なパラメータ、ξは重要でない知る必要のないパラメータである
任意のθ、ξにおいて以下の3つを満たす時、f(x,θ)は推定関数と呼ばれる
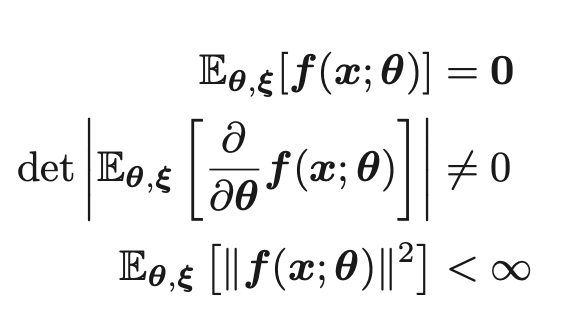
真のモデルp(x;θ∗,ξ∗)から独立にサンプル{x1,··· ,xT}が得られるとする。もし推定関数f(x,θ)が存在するなら、推定方程式
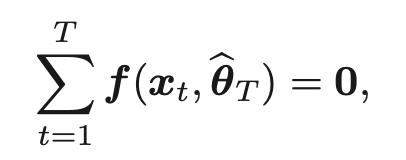
を解くことで推定量を得ることができる
//メモ 推定量・・・パラメータ
この式の解はM-推定量と呼ばれる
M-推定量は、重要でないパラメータξによらない、真のパラメータに収束する
推定関数の強みは、推定関数となり得る関数系全体を特定できれば、全てのM-推定量を含む一致推定量のクラスを特定できることである
推定量のクラスを特定できれば、下記の式より全てのM-推定量の推定精度を求めることができる。
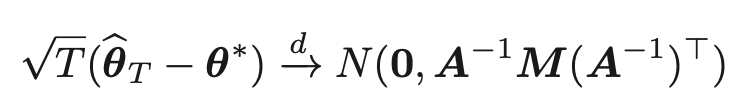
さらに、最良の推定精度を実現する推定量を求めることで、最適なM-推定量を導出できる
推定関数に基づく方策評価の理論解析
推定関数はマルコフ報酬過程でも扱えるように拡張してある(マーチンゲール推定関数)
推定方程式
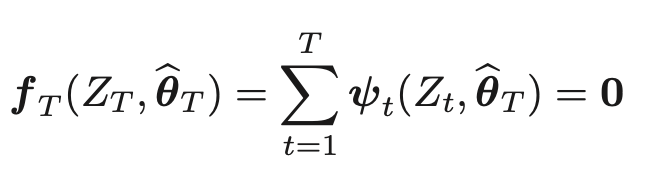
を解くことで、M-推定量を得ることができる
マーチンゲール推定関数となりうる関数クラス
証明は省略

これまで提案されている代表的な方策評価法は、上記から計算できるM-推定量により、すべて説明できる
最適な推定精度を実現する M-推定量
定理1により、全てのマーチンゲール推定関数を特定できたため、すべてのM-推定量に対して推定精度を知ることができるようになった
証明は省略
既存手法との関係
既存手法は、M-推定量を求める計算法であると見なすことができる。
既存手法は、2種類に分けられる
バッチ法
逆行列演算により、一撃で推定量を計算する
M-推定量との関係