強化学習　文献まとめ5

リレー解説　強化学習の最近の発展　第14回
松井藤五郎　「複利型強化学習―強化学習のファイナンスへの応用―」
計測と制御 第52巻 第11号 2013年11月号　P1022-1027
https://www.jstage.jst.go.jp/article/sicejl/52/11/52_1022/_article/-char/ja/

をまとめた個人用メモ

※この記事をまとめたのは2021年5月あたりで、強化学習について勉強し始めのときにまとめたもので、間違った内容が含まれている可能性があります

前回：https://qiita.com/he-mo/items/c940261bbfec5ce90fdb
本記事が最終回です

1.はじめに

強化学習を金融商品の取引に適用する研究が行われてきたが、その目的はエージェントの報酬（利益）を最大化することであった。
しかし、ファイナンスの現場で望まれていることは利益率の複利効果を大きくすることであり、従来の強化学習によって報酬を最大化しても利益率の福利効果は最大化されないことが明らかになった。

利益率・・・利益/売上、売上高に対する利益の割合
複利効果・・・運用で得た収益を当初の元本にプラスして再び投資することで、利益が利益を生み、ふくらんでいく効果¹

そこで、この文献の筆者らはエージェントが報酬の代わりに利益率を受け取るものとした上で、利益率の複利効果を最大化する強化学習の枠組みを開発した。これを複利型強化学習(Compound Reinforce- ment Learning)という。

2.利益率の複利効果と投資比率

利益率とは、ある投資における投資金額の利益の割合である。時刻tにおける投資金額がp_t、時刻t+1における利益がr_t+1の時、時刻t+1における利益率R_t+1は以下のように定義される。

R_t+1=r_t+1/p_t

例えば100円で仕入れた（投資した）ものを120円で売った時、利益は100-120で20円、利益率は20/100=0.2となる。

利益率R_t+1の金融商品に全財産を投資すれば、資産総額は1+R_t+1倍(上記の例だと1+0.2=1.2倍)になるが、全財産のうちfだけを投資した場合は資産総額が1+R_t+1f倍になる。この資産総額に対する投資金額の比率を(fのことを)投資比率という。

例えば、資産総額100万、投資比率f=0.5、利益率R_t+1=0.2の金融商品に投資した時、投資金額は100万 * f = 50万、利益は50万*0.2=10万となり、資産総額は110万となる。

t期の利益率R₁、R₂、・・・、R_tである金融商品における利益率の複利効果である複利利益率G_tは以下のように表される。

また、fを考慮した場合は以下のように表される。

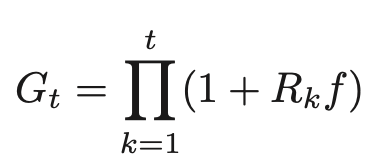
つまり、この金融商品に投資比率fで投資し続けると、時刻tに資産総額はG_t倍になる。

利益率の複利効果は、利益率の幾何平均によって評価される。この金融商品に投資比率fで投資し続けた場合、幾何平均利益率は以下のように表される。

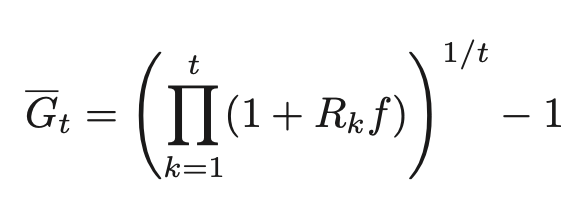
利益率の複利効果を理解するために、3本腕のバンディット問題を考える。あるカジノに下記のような3台のマシンが置いてある。

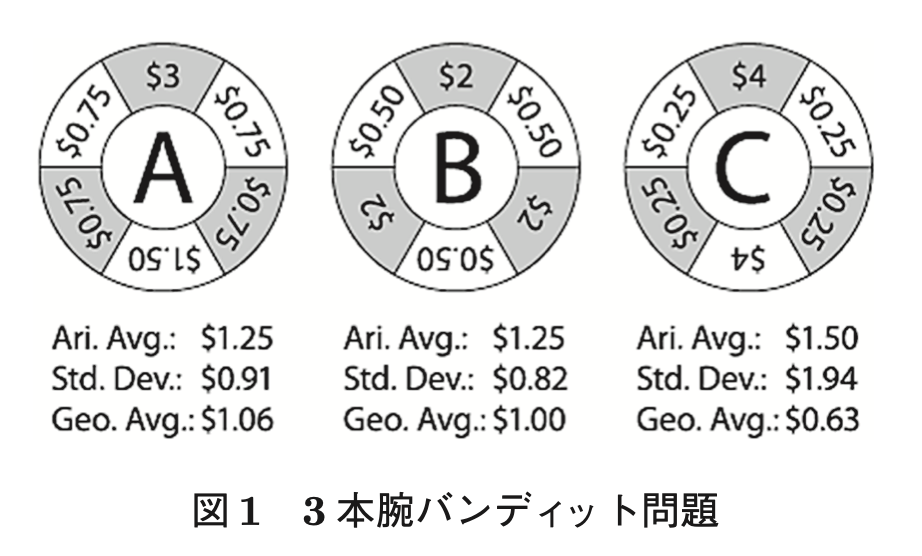
円盤を回転させ、円盤が停止した時に矢印が示す場所によって払い戻しを受け取る。円盤には掛け金1ドルあたりの払い戻し金額が表示されている。100ドルもっていて100回遊べるとすると、どのマシンを選ぶべきであろうか。

Ari.Avg・・・払い戻し金額の平均
Std.Dev・・・払い戻し金額の標準偏差
Ger.Avg・・・幾何平均利益率

答えは、最も幾何平均利益率が高いAである。Aに払戻金を含めて全財産をかけると、幾何平均利益率が6%であるため100回遊んだ後の資金の期待値は36,110ドルとなる。
これに対し、払戻金額の平均が最も高いCに同じことをした場合、幾何平均利益率が-37%であるため、100回遊ぶ頃にはほぼ0になってしまう。

このマシンのように、利益率の確率分布が既知である時、利益率の複利効果を最大化する投資比率fが解析的にもとまる（ケリー基準という）
このマシンの場合、Aのケリー基準は69%で、これは全財産の69%を賭け続けた時に利益率の福利効果が最大になることを示しており、この時の幾何平均利益率は7%となる。
Cでさえ、ケリー基準の22%を賭け続けた場合幾何平均利益率は5%になる。

このように、利益率の福利効果の最大化をするためには、利益率の幾何平均と投資比率を考慮しなければならない。

3.複利型強化学習

3.1 複利型強化学習の枠組み

従来の強化学習が割引収益r_t+1γr_t+2+γ²r_t+3・・・を最大化する行動規則を学習するのに対し、複利型強化学習は二重指数関数による割引複利利益率

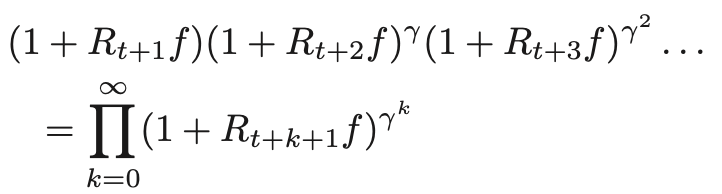
の対数期待値を最大化する行動規則を学習する。
複利型強化学習において状態価値と行動価値は以下のように表される

ここで、P^a_{s s'}は状態sにおいて行動aを行った時に次の状態がs'になる確率で、R^a_{s s'}は、状態sにおいて行動aを行ってつぎの状態が s′になったときに得られる利益率Rfに1を加えたものの対数の期待値以下であり、以下で表される。

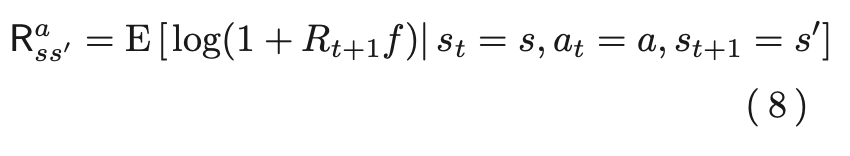
複利型強化学習では、このQ^π(s,a)を最大化するような行動規則πを学習する。

3.2 複利型Q学習

従来のQ学習とは異なり、Q値を以下の更新式で更新する。

αは学習率パラメータ
複利型Q学習のアルゴリズムをいかに示す。

4.投資比率の最適化

複利型強化学習では、新たなパラメータとして投資比率fが導入されている。このfを幾つにするかが問題となる。
この文献の筆者は、fをオンライン勾配法を用いて最適化する方法を提案した。
この方法では、時刻t+1までの複利利益率

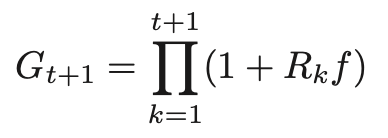
をfをパラメータとする関数とみなし、G_t+1を最適化するようなfをオンライン勾配法によって求める。
fは以下のように更新される

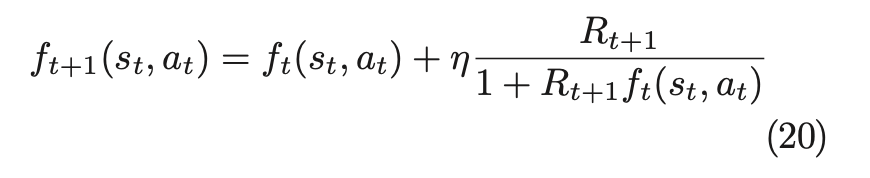
1. りそなグループ.「実はすごい「複利」の効果！将来に備えて複利運用で資産を育てよう」　.https://www.resonabank.co.jp/kojin/shisan/column/kihon/column_0015.html .参照：2021年6月12日 ↩