はじめに
二度目の投稿になります、@reonyanarticleです。
大遅刻をしてしまいましたが、なんとか書き終えたので投稿させていただきます。
今回書かせていただくのは、正規表現に関する話です。
正規表現と自然言語処理は切っても切れない関係にあります。
文中に存在するいらない単語を削除するためや、置換を行うため、awkやgrepを使う時など、使う時の話をすると枚挙に暇がありません。
そんな身近な正規表現に関することを書こうとおもったのですが、正規表現の書き方に関する記事はたくさん存在するので、私が書いても今ひとつ面白みがありません。
なので今回は、正規表現がどのようにマッチングを確認しているのかを少し話ができたらいいなと思っています。
但し書きとして、正規表現の演算子に関する話は話さないのと、数学の言葉をめちゃ使います。気になるという方は調べたりしてみてください。
また、ちょくちょく未定義語がでてきますが徐々に改修していこうと思います。
正規表現の定義
私が参考にした本に『正規表現とは一種の「式」 (expression)なわけです。』と書かれています。特定の文字列の集合を表すための「式」が正規表現ということなのです。
例えば、文字aとbだけをつかって、aが一つだけ出現する文字というと、aやabbbbbb、bbbbab、abなどがありますが、「aが一つだけ出現する文字」というのは無限に存在します。全てを書くことはできません。しかし、正規表現をもちいれば、b*ab*という一つの式で記述することができるということです。(私は集合における内包表記的なものだという認識でいます。)
処理系の違い
簡単に正規表現の定義に触れたところで、次に正規表現のマッチングがどのように確認されているかを説明します。
処理系には二種類あり、DFA型とVM型があります。
- DFA型:正規表現を決定性有限オートマトン(DFA)に変換してマッチングを行います。GNU grepの処理系などがあります。
- VM型 : 正規表現をバイトコードに変換してマッチングを行います。Python, JavaScriptなど大体のスクリプト言語の処理系などがあります。
実際行っている仕組みは参考文献の図を参考にすると、以下のようになっています。
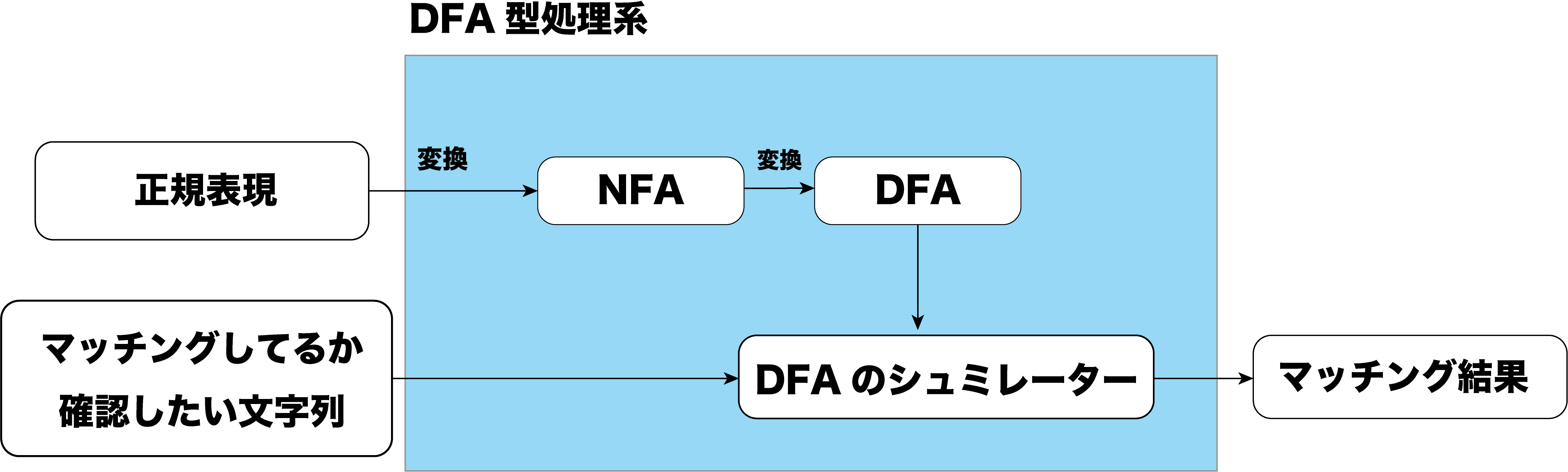
(今回はVM型のマッチングの仕組みは説明しません。参考文献を読んで確認してみてください!)
正規表現に対応するDFAを構成して、そのDFAに与えられた文字列が通るか通らないかをみることでマッチングを確かめています。
今回、Pythonを使って、DFA型の(簡単な)処理系を作成しようと思います!
そのために先ほどからでているDFAの定義からはじめていきます。
DFAの定義と例
DFAの定義
決定性有限オートマトン5つ組 ${\mathcal A} = \langle Q, \Sigma, \delta, s , F \rangle$である。ここで、
- $Q$は状態と呼ばれる有限集合
- $\Sigma$は文字を集めた有限集合
- $\delta : Q \times \Sigma \rightarrow Q$は遷移関数と呼ばれる状態と文字を受け取って状態を返す関数
- $s \in Q$を初期状態という
- $F \subset Q$を受理状態という。
DFAの例
上の定義だけでは何を言っているのかわからないと思うので、例に触れてみましょう。
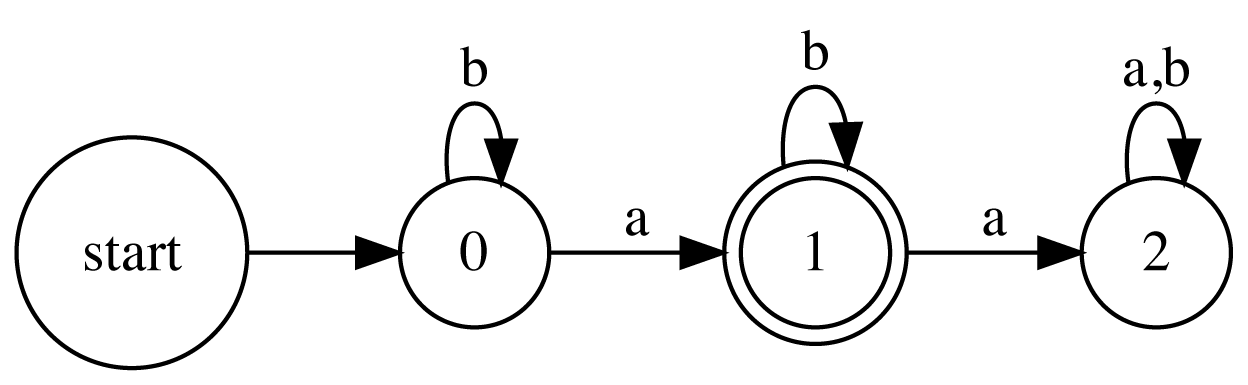
最初からたくさんの文字を扱うと大変なので、使える文字が、aとbだけにして、b*ab*という、aが一つだけ出現するという正規表現をDFAをつかって書いてみましょう。
$\Sigma =\{ a,b \}$として、$Q =\{0, 1, 2\}$とします。また、$s = 0$、$F=\{ 1\}$として、遷移関数を以下のように定義します。
- $\delta(0, a) = 1$
- $\delta(0, b) = 0$
- $\delta(1, a) = 2$
- $\delta(1, b) = 1$
- $\delta(2,a) = 2$
- $\delta(2,b) = 2$
5つ組が定義できたので、aが一つだけ出現するDFA、${\mathcal A}$は以下のようになります。
DFAの定義と例にふれて、なんとなくDFAがなんとなくわかりましたかね?わからなかったら参考文献を書いておくので、そちらを読んでみると詳細がわかるかもです。
DFAをつかったマッチング
さて、DFAが定義できたので、DFAが文字列を受理するを定義し、実際にマッチングするかどうかを確認してみましょう。
DFAが文字列を受理するの定義
DFAを${\mathcal A} = \langle Q, \Sigma, \delta, I , F \rangle$とし、文字列を$w=w_0 \cdots w_n$$(w_i \in \Sigma)$とする。この時、以下の三条件を満たす、状態列$\{r_0 , \ldots, r_n \} \subset Q$が存在する時、${\mathcal A}$は$w$を受理するという。
- $r_0 = s$
- $i < n$のとき、$\delta(r_i, w_i) = r_{i+1}$
- $r_n \in F$
DFAが文字列を受理するの例
DFAが文字列を受理するの定義も見てすぐわからないと思うので、具体例をみていきます。
先ほどと同じ、b*ab*という、aが一つだけ出現するという正規表現についてふれていきます。
この正規表現に関して、abという文字列と、bbbabaという文字列を考えてみましょう。
abという文字列に関して、$\{0,1\} \subset Q$という状態列を考えます。すると、$\delta(0, a) = 1$、 $\delta(1, b) = 1$となり、$0=s$で、$1 \in F$で受理するの条件を満たしています。したがって${\mathcal A}$はabを受理します。これが、DFAでマッチングしているということになります。
次に、bbbabaに関してですが、どんな状態列をとってきても${\mathcal A}$に受理されません。
bbbabaを単純に推移させる$\{ 0, 0, 0, 1, 1, 2\} \subset Q$を考えてみます。$\delta(0, b) = 0$、$\delta(0, b) = 0$、$\delta(0, b) = 0$、$\delta(0, a) = 1$、$\delta(1, b) = 1$、$\delta(1, a) = 2$となり、$2 \notin F$なので、満たしません。なので、bbbabaは受理されません。
しかし、部分文字列であるbbbabや、bbbaは受理されます。上の状態列の部分列である、$\{ 0, 0, 0, 1, 1\}$、$\{ 0, 0, 0, 1\}$がそれぞれ条件を満たしているからです。
これを用いて、最短マッチングを「DFAが文字列の部分文字列で受理するもののうち、長さが最小のもの」と定義することができます。
これで、具体的ではありますが、正規表現からDFAが生成され、文字列が正規表現とマッチするかをDFAを用いて確認することができました!
Pythonを使った実装
それでは実際にPythonを使って実装をしてみましょう。DFAは具体的な正規表現を与えないと作ることができないので、今回もb*ab*を使いましょう。本当は一からDFAも実装できればいいのですが、作者のいろんな都合により、automataというモジュールをつかいます。頑張れば自作することも可能なのでぜひ頑張ってみてください!(DFAのモジュールをつくるのは骨が折れると思います。)
from automata.fa.dfa import DFA
dfa = DFA(
states={'0', '1', '2'},
input_symbols={'a', 'b'},
transitions={
'0': {'a': '1', 'b': '0'},
'1': {'a': '2', 'b': '1'},
'2': {'a': '2', 'b': '2'}
},
initial_state='0',
final_states={'1'}
)
def is_accepted(words: str):
if dfa.accepts_input(words):
print('受理されます。')
else:
print('受理されません。')
def check_min_matching(words: str):
i = 0
while i < len(words):
if dfa.accepts_input(words[:(i+1)]):
print(f'{words[:(i+1)]}が受理されました。')
break
else:
i = i + 1
else:
print(f'{words}は受理されませんでした。')
if __name__ == "__main__":
is_accepted('ab')
is_accepted('bbaba')
check_min_matching('ab')
check_min_matching('bbbaba')
check_min_matching('bbb')
実行してみると以下の出力結果が返ってきます。
受理されます。
受理されません。
aが受理されました。
bbbaが受理されました。
bbbは受理されませんでした。
無事に、b*ab*をDFAで表現できましたね!
実際に行っている図を今度頑張って図示しますので少々おまちください。
最後に
今回はb*ab*に関してだけですが、処理系を作成することができました。実際にどのように正規表現のマッチングを確認しているかをDFAを通じて知るとより正規表現のことを知れるかなと思います。
さて、読んでいる方の中には正規表現全部がDFAで書けるのか?と思う方もいらっしゃるかと思います。実はこんな定理が存在します。
Kleeneの定理
有限文字集合$\Sigma$上の任意の言語$L$について、次の 3 つの命題は等価である。
- 言語$L$は正規表現で表現できる
- 言語$L$はオートマトンで認識できる
つまり、正規表現で書けるものはオートマトンで受理できて、オートマトンで受理できる言語は正規表現で書けるということです。
この定理があるため、*以外の演算に関しても、DFAを作成することができることがわかります。
すごいですね!(すごいことを伝える能力が足りない。。。)
ぜひ、他の演算についてや、文字の数を増やした正規表現について自分でDFAを作ってみてください!楽しいですよ!
この記事では紹介できなかった定理や、DFAや正規表現に関する面白い話がたくさんあります!是非参考文献をみてみてください。
明日私が24日の記事を出す前に、@jyamiがgoでシェルもどきを作る話を書いてくれてました!
お疲れ様でした!
参考文献
私が昔形式言語を学ぶ際に読んだ本は以下です。
今回、正規表現について勉強に使った本は以下です。途中の図や、説明を少し参照させていただきました。
読んでてとても楽しかったのでぜひ読んでみてください。
余談ですが、この本の著者の一人である新屋 良磨さんは正規表現やオートマトンに関わるスライドをたくさんネットにあげているのでぜひそれも見てみると面白いですよ!