はじめに
今回はアンサンブル学習の中のAdaboostについて理論まとめていきます。
この辺りの話は用語が多くてこんがらがってしまうので、先にアンサンブル学習に用いられる用語の解説を行います。
AdaBoostの理論はその後にまとめるので、そちらを早く見たい方は飛ばして下さい。
今回の記事を書くに辺り、以下の記事がとても参考になりました。
ブースティングとアダブースト(AdaBoost)について詳しく解説
それでは頑張っていきましょう。
アンサンブル学習とは
アンサンブル学習とは、複数の学習機を組み合わせてより良い予測を得ようとするテクニックです。
多くの場合、単一のモデルを用いるよりも良い結果が得られます。
どのように複数の学習器を組み合わせるのかというと、分類の場合は複数の学習器の多数決をとり、回帰の場合は複数の学習器の平均をとります。
アンサンブル学習においてよく用いられるテクニックとして、バギングやブースティング、スタッキングやバンピングなどがあります。
ランダムフォレストは、この中でもバギングというテクニックを用いて、学習器として決定木を用いたアンサンブル学習だといえます。
沢山の用語がでてきて分かりにくくなりましたね。それぞれのテクニックについて解説していきます。
バギングについて
Bagging(バギング)は、bootstrap aggregatingの略です。
ブーストトラップというテクニックを用いて、一つのデータセットからいくつものデータセットを作成し、その複製したデータセット一つにつき一つの学習器を生成し、そのようにして作成した複数の学習器の多数決を行うことで最終的な予測を行います。
ブーストトラップとは、データセットから重複を許してn個のデータをサンプリングする方法です。
データセットを$S_0 = (d_1, d_2, d_3, d_4, d_5)$として、n=5個のデータをサンプリングするときは$S_1 = (d_1, d_1, d_3, d_4, d_5)$や$S_2 = (d_2, d_2, d_3, d_4, d_5)$などのデータセットを作成することになります。
このように、ブーストトラップを用いると一つのデータセットからいくつもの異なるデータセットを作成できることが分かりますね。
具体例で予測値を考えていきましょう。
訓練データセットから大きさnのブーストトラップデータ集合をN個生成します。
それらのデータを用いてN個の予測モデルを作り、それぞれの予測値を$y_n(X)$とします。
このN個の予測値の平均が最終的な予測値になるので、バギングを用いたモデルの最終的な予測値は以下のようになります。
y(X) = \frac{1}{N}\sum_{n=1}^{N}y_n(X)
これでバギングの解説は終わりです。次はブースティングをみていきましょう。
ブースティングについて
ブースティングでは、バギングのように弱学習器を独立に作るのではなく、1つずつ順番に弱学習器を構成していきます。その際、k 個目に作った弱学習器をもとに(弱点を補うように)k+1 個目の弱学習器を構成します。
弱学習機を独立に生成するバギングと違い、一つずつ弱学習機を生成しなければならないブースティングは時間かかります。その代わり、ブースティングの方がバギングに比べて精度が高い傾向にあります。
スタッキング
バギングはN個の予測値の単純平均を考えました。
このアルゴリズムでは個々の予測値を平等に評価しており、それぞれのモデルの重要度を考慮できていません。
スタッキングは個々の予測値に重要度に応じて重みを追加し、最終的な予測値とします。
以下の式で表されます。
y(X) = \sum_{n=1}^{N}W_ny_n(X)
バンピング
バンピングは複数の学習器の中から最も当てはまりの良いモデルを探すための手法です。
ブーストトラップデータ集合を用いてN個のモデルを生成し、それを用いて作成した学習器を元のデータに当てはめ、予測誤差が最も小さいものを最良のモデルとして選びます。
あまりメリットがない方法のように思われますが、この手法により質の悪いデータを用いて学習してしまうことを避けることができます。
AdaBoostの理論について
それではAdaBoostの理論について解説していきます。
AdaBoostも勾配ブースティングもブースティングの一種であるので、弱学習機を逐次的に生成していくアルゴリズムになります。
大きく分けて以下の四つの特徴があります。
-
弱学習機の訓練において、重み付けられたデータ集合を利用する
-
前の学習機が誤分類したデータ点に大きな重みを与える
-
最初は全てのデータに均等な重みを与える
-
そのように生成・訓練した弱学習機を組み合わせて最終的な予測値を出力する
このように、AdaBoostは誤分類したデータを重要視することによって制度を高めようとするアルゴリズムであるといえます。
イメージは以下になります。
extracted from Alexander Ihler's youtube video
それでは、実際にどのように誤分類したデータに重みを与えていくのかを数式で見ていきましょう。
できるだけ分かりやすく解説するので、頑張ってください。
N個のデータを分類するために、弱学習機をM個生成する場合を考えます。
最終的な強学習機のアウトプットは以下のようになります。
H(x) = sign(\sum_{m=1}^{M}α_my_m(x))
signは符号関数と呼ばれ、引数が0より小さければ-1を、0より大きければ1を返す関数です。$y_m(x)$が弱学習機で、$α_m$がそれぞれの弱学習機の重みになります。
つまり、弱学習機に重みを加えてその和をとり、その合計が0より大きければ1を、0より小さければ-1を返し、それを最終的な出力にしています。それでは、$y_m(x)$と$α_m$をどのように決定しているのかを見ていきましょう。
yとαの決定
最初のデータに対しては均等な重み与えるので、$n = 1,2,3,...,N$のデータの重み係数{$W_n$}を$w_n^{(1)}=\frac{1}{N}$に初期化します。
wの右下がデータの番号で、wの右上が弱学習機の番号です。つまり、1つ目の弱学習機においては全てのデータの重みを$\frac{1}{N}$にします。
全ての学習機 $m=1,2,3,...M$ に対して以下の操作を繰り返します。
- 以下を誤差関数と定義し、これを最小化する。
J_m = \sum_{n=1}^{N}w_n^{(m)}I(y_m(x_n)\neq t_n)
$w_n^{(m)}$はm番目の弱学習機のn番目のデータにおける重みです。
$I$は支持関数と呼ばれ、$y_m(x_n)\neq t_n$のとき、つまりある一つのデータにおける予測値と正解ラベルが一致しないときには1を返し、$y_m(x_n) = t_n$のとき、つまりある一つのデータにおける予測値と正解ラベルが一致するときには0を返します。
つまり、$J_m$はある弱学習機$m$において、予測ミスをしたデータ点の重みの和になります。
- 次の式を用いてαを計算する
\epsilon_m = \frac{\sum_{n=1}^{N}w_n^{(m)}I(y_m(x_n)\neq t_n)}{\sum_{n=1}^{N}w_n^(m)}
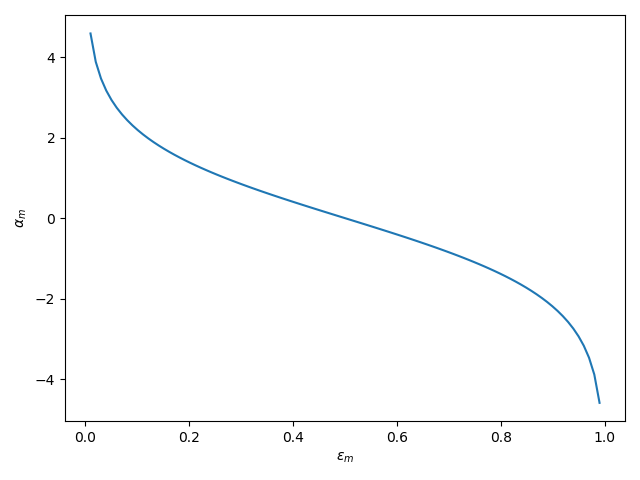
\alpha_m = ln \bigl(\frac{1-\epsilon_m}{\epsilon_m} \bigr)
$\epsilon_m$の分母は弱学習機$m$におけるデータの重みの和であり、分子はある弱学習機$m$において、予測ミスをしたデータ点の重みの和になります。
つまり、$\epsilon_m$は誤差率を重みで表したものということができます。
以下に図示しました。
H(x) = sign(\sum_{m=1}^{M}α_my_m(x))
つまり、誤差率が高い($\epsilon_m$が大きい)学習機の重み$\alpha_m$はマイナスに、誤差率が低い($\epsilon_m$が小さい)学習機の重みをプラスにして足し合わせ、合計が正の値なら$H(x)=1$が、合計が負の値なら$H(x)=0$を最終的な出力とします。
- データ点の重みを更新する
データ点の重みを以下の式で更新します。
w_n^{(m + 1)} = w_n^{(m)}exp \bigl(\alpha_mI(y_m(x) \neq t_n) \bigr)
弱学習機$m$における$n$番目のデータの予測値が正解ラベルと一致していればデータの更新は行わず、予測値と正解ラベルが異なっていた場合のみ$exp(\alpha_m)$を掛けて重みを更新します。
以下に$\alpha$と$exp(\alpha_m)$の関係を図示します。
誤差率$\epsilon_m$が高い学習機においては$\alpha_m$が小さくなるため、$w^{(m+1)}$は小さくなります。
誤差率$\epsilon_m$が低い学習機、つまり正確な学習機においては$\alpha_m$が大きくなるため、$w^{(m+1)}$は大きくなります。
つまりまとめると、正確な学習機においては間違えたデータの重みを大きくして次の学習機に渡すことになり、不正確な学習機においては、間違えたデータの重みを小さくして次の学習機に渡すことになります。
以上がAdaBoostの理論になります。
終わりに
ここまで読んでくださり、ありがとうございました。
気が向いたら、実装の方もまとめていきたいと思います。