はじめに
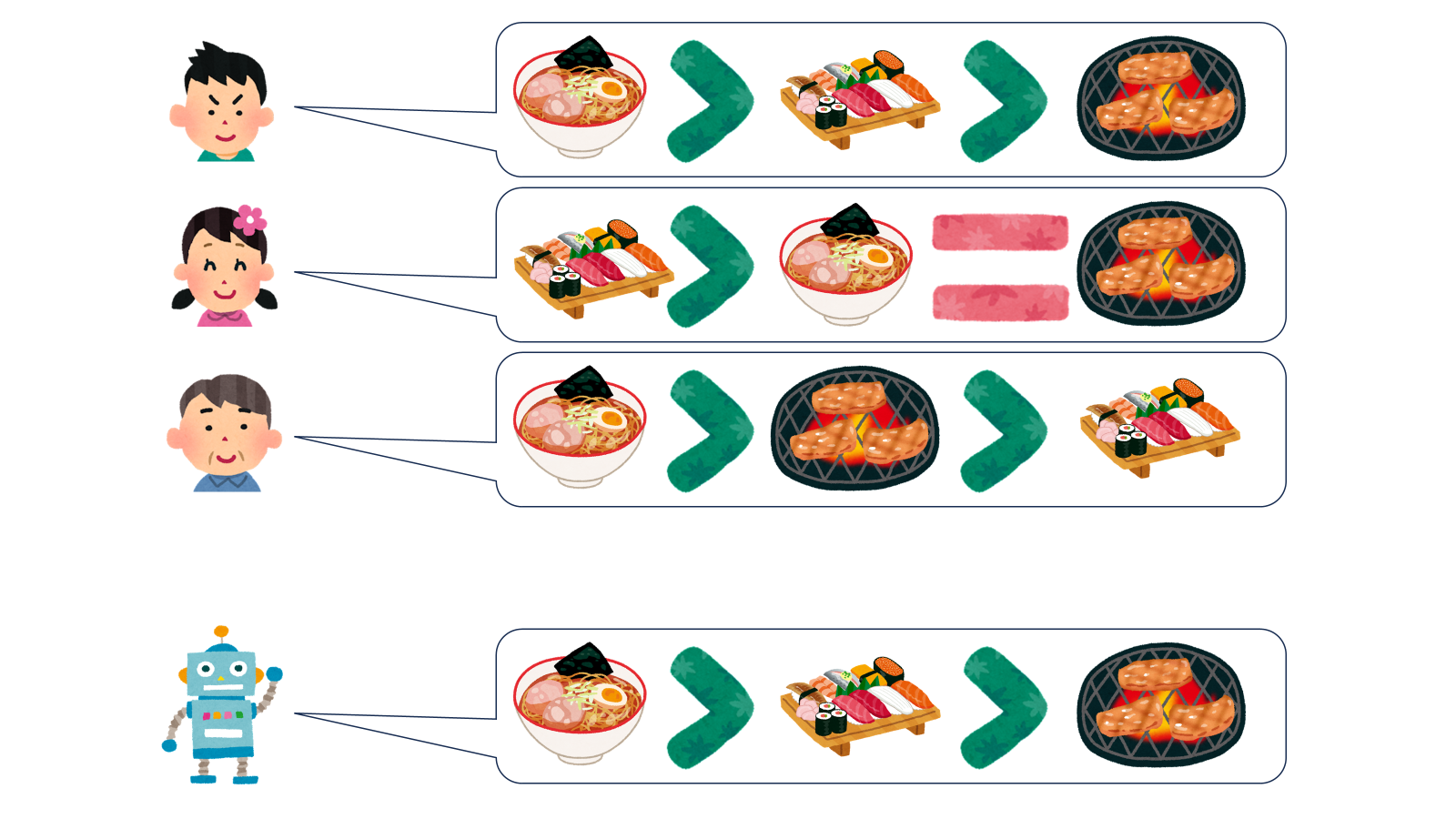
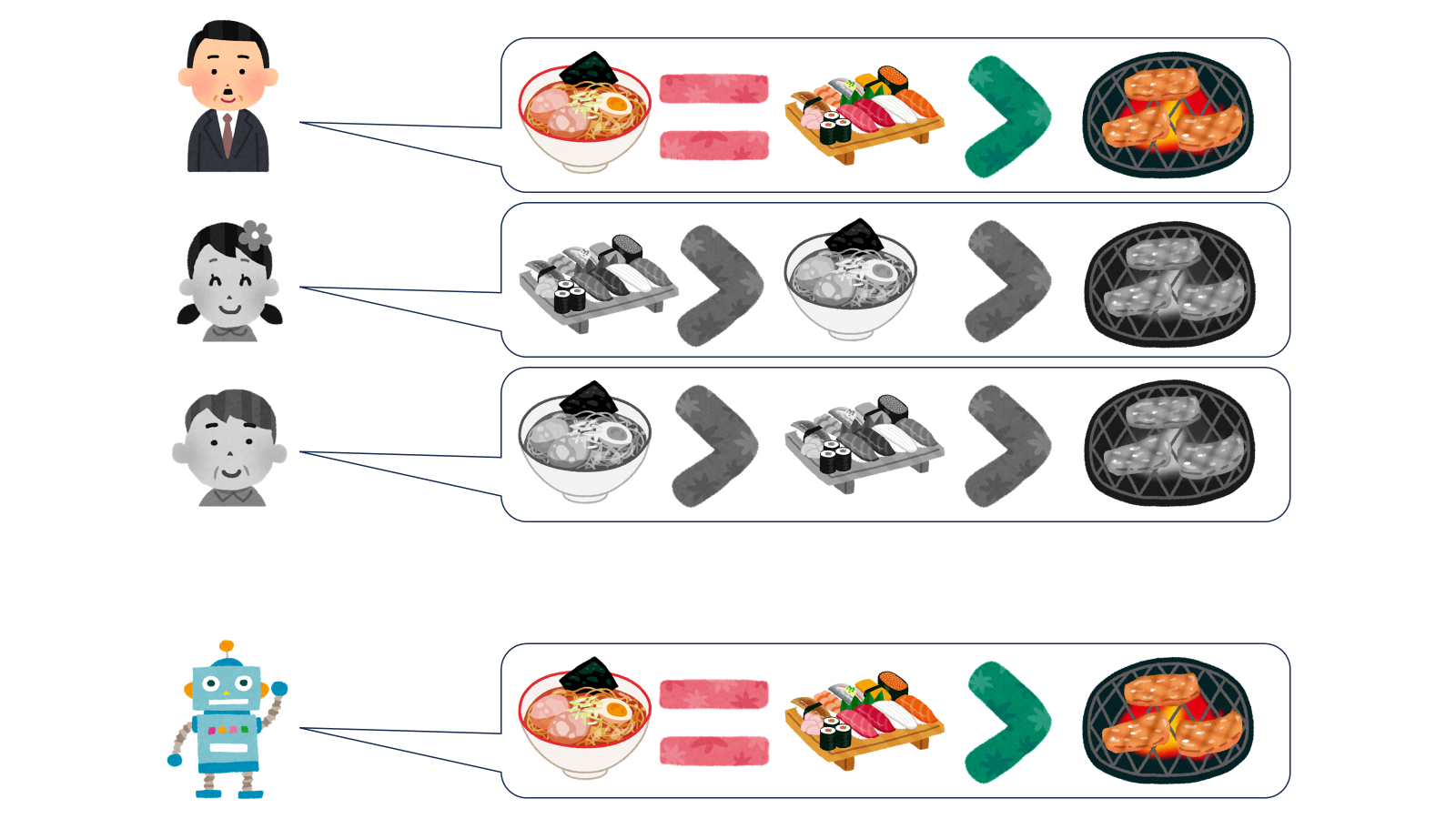
とある国で「人気の食べ物決定戦」が開かれることになりました。国民たちはそれぞれが好きな食べ物を順位付けして投票し、それらをうまく集計した結果を最終的に発表します。
真ん中の女の子のように「同じくらい好き」という投票もアリです。
さて図に示されている通り集計はロボットくんがやってくれるわけですが、あまり杜撰な集計をされても困ります。そこでロボットくんに守ってほしいルールが三つあります。
その1:「弱パレート最適」であること。
投票者の全員がラーメンをカレーより好んでいたとします。このとき、最終的な集計結果が「ラーメンの人気はカレー以下」だったらおかしいですよね。
全員ラーメンがカレーより好きであるならば、ラーメンの順位をカレーより上にすることによって投票者の全員がより幸せになるはずです。このような改善を「強パレート改善」といい、「もうこれ以上強パレート改善はできない」という状態を「弱パレート最適」といいます。言い換えると、すでに弱パレート最適である状態を変更すると少なくとも一人は今以下の望ましさになってしまいます。ただし「以下」ということは「変化なし」ということもありえるので、弱パレート最適な状態においては「全員を今より幸せにする」ことはできずとも「一人の犠牲者も出すことなく誰かを幸せにする」ことはまだ可能である可能性はあります。
「弱パレート最適」があるということは「強パレート最適」もあります。アローの不可能性定理の証明には関係ないのですが、せっかくなのでざっくりと解説していきます。
「全員を今よりも幸せな状態にすること」を「強パレート改善」といいましたが、これを少し緩和し、「全員を今以上に幸せで、かつ少なくとも一人を今より幸せにすること」を「弱パレート改善」といいます。つまり一人の犠牲者も出すことなく、少なくとも一人を幸せにするということです。
そして「もうこれ以上弱パレート改善はできない」という状態を「強パレート最適」といいます。言い換えると、すでに強パレート最適である状態を変更すると「変化なし」か「少なくとも一人の犠牲者が出る」かのどちらかになってしまいます。つまり強パレート最適な状態において誰かを今より幸せにしようとすると必ず犠牲者が出ます。
その2:「無関係な選択肢の影響を受けない」こと。
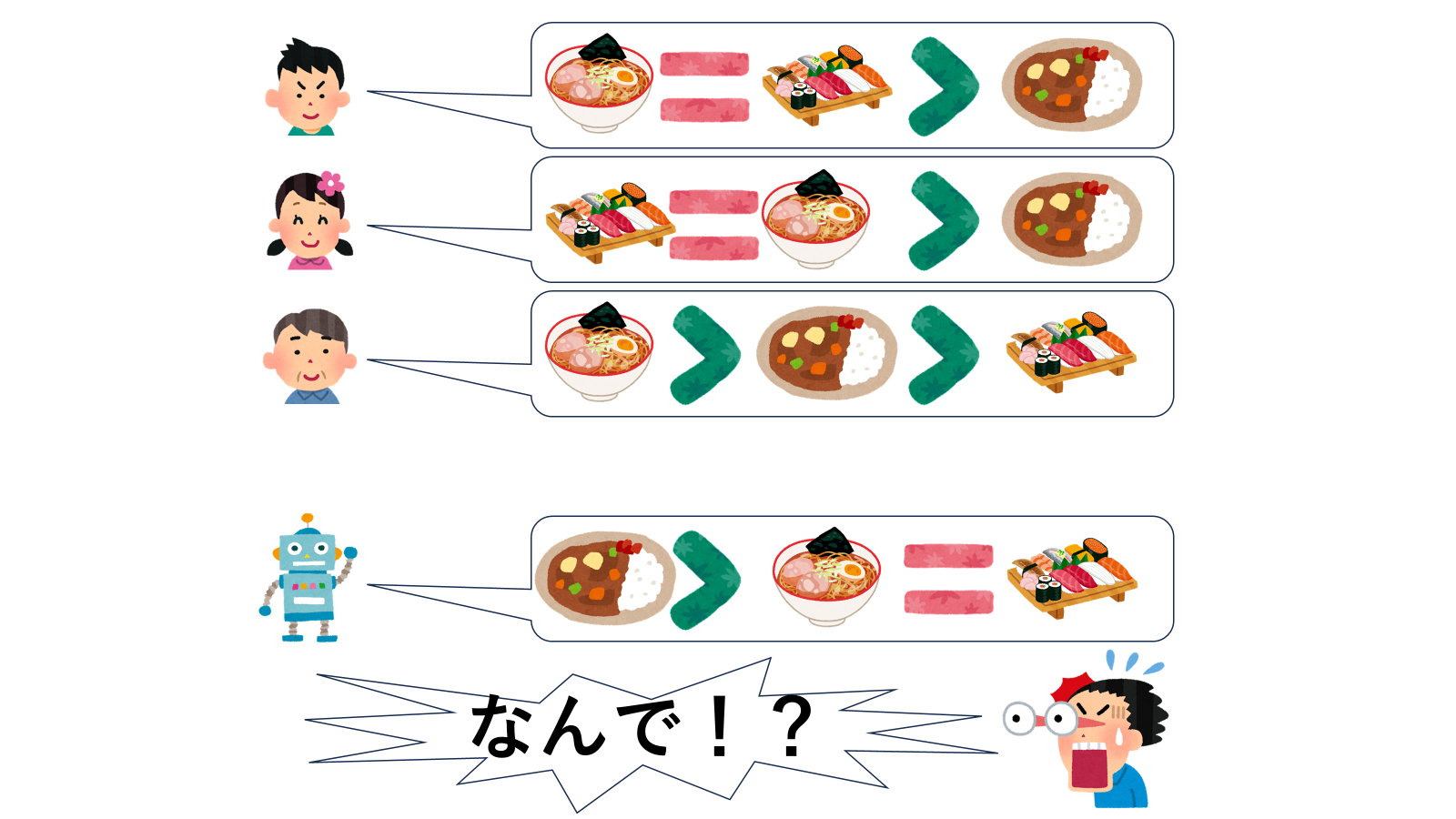
ある年の選挙では集計の結果「お寿司が焼肉よりも人気」という結果になりました。
ところがここで選挙管理委員会が「ごめん!投票対象にからあげを入れるの忘れてた!もう一回投票と集計をやり直してくれ!」と言い出しました。国民たちはめんどくさそうな表情を浮かべながらも再投票を行ったのですが、集計の結果なんと焼き肉がお寿司よりも人気になってしまいました。
投票対象にからあげがあろうがなかろうが、各国民がお寿司と焼肉のどちらをより好むかには関係ないはずですし、最終的な集計結果においてお寿司と焼肉のどちらが人気かにも関係ないはずです。したがってロボットくんには「投票対象が増えたり減ったり変わったりしても、食べ物 A と食べ物 B の順序は変わらないこと」が求められます。これが「無関係な選択肢の影響を受けない」ということです。
その3:「独裁者が存在しない」こと。
弱パレート最適でなかったり無関係な選択肢の影響を受けたりするような集計方法ではいけません。そこである男が、弱パレート最適で、しかも無関係な選択肢の影響を受けない画期的な集計法を考案しました。こんな方法です。
一番最初に投票したその男の投票のみを採用し、そのあとの投票すべてを破棄するというやり方です。この方法は確かに弱パレート最適でしかも無関係な選択肢の影響を受けません。つまり男の言ったこと自体は嘘ではないのですが、しかしこんな選挙に国民が納得するはずもありません。言い換えれば、選挙には独裁者が存在してはいけません。
アローの不可能性定理
まとめると、選挙には以下の三つの性質が求められます。
- 弱パレート最適であること
- 無関係な選択肢の影響を受けないこと
- 独裁者が存在しないこと
このような選挙方法は存在するでしょうか?
例として、カレーとラーメンのたった二つのみが投票対象である場合を考えましょう。このときはごく単純な多数決という集計方法で上の三つを満たせます。つまり、カレーをラーメンより好む人と、ラーメンをカレーより好む人のどちらが多いのかを比べるだけで「弱パレート最適性」「無関係な選択肢からの独立」「独裁者の不在」の 3 性質をすべて満たせます。
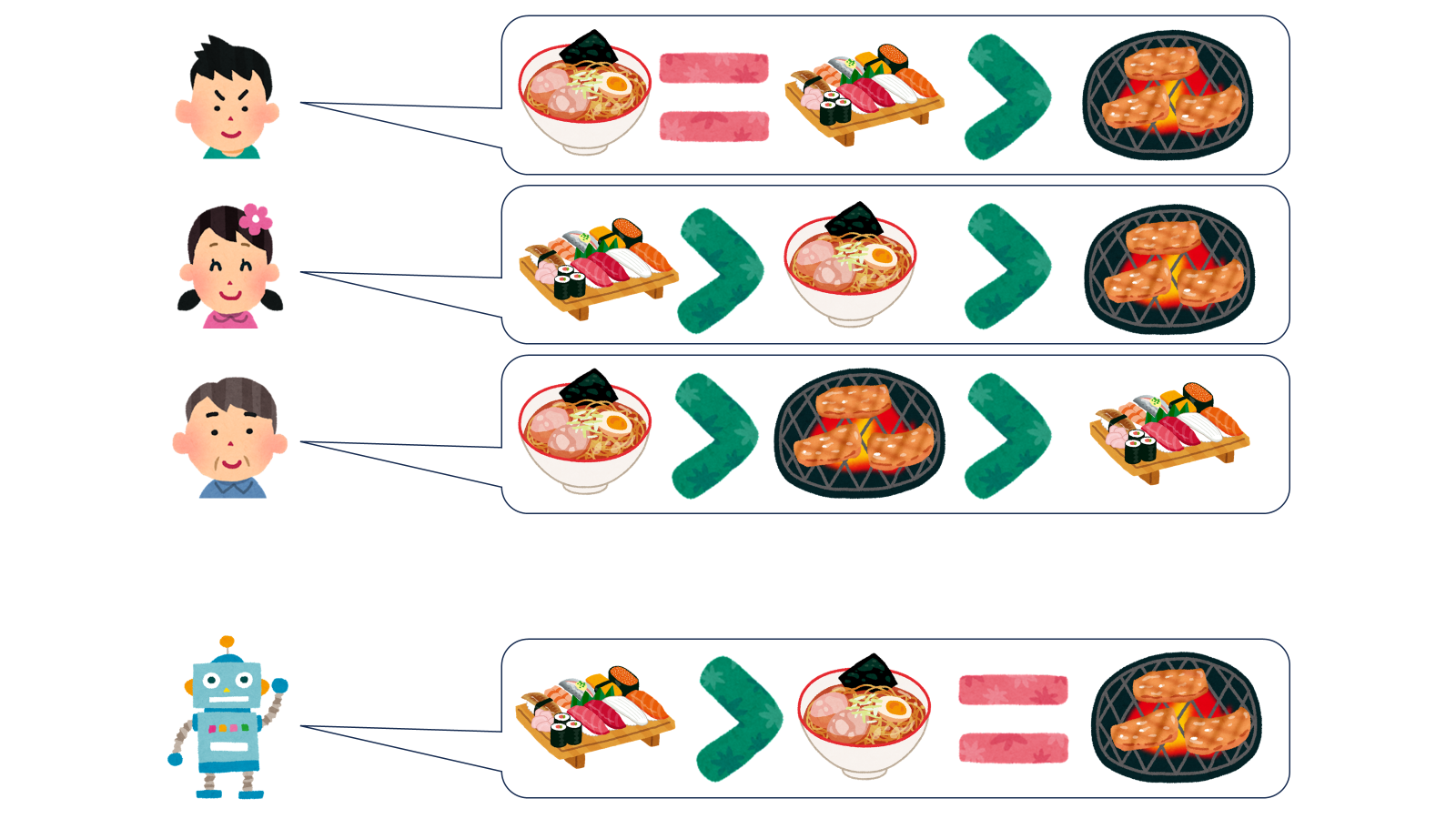
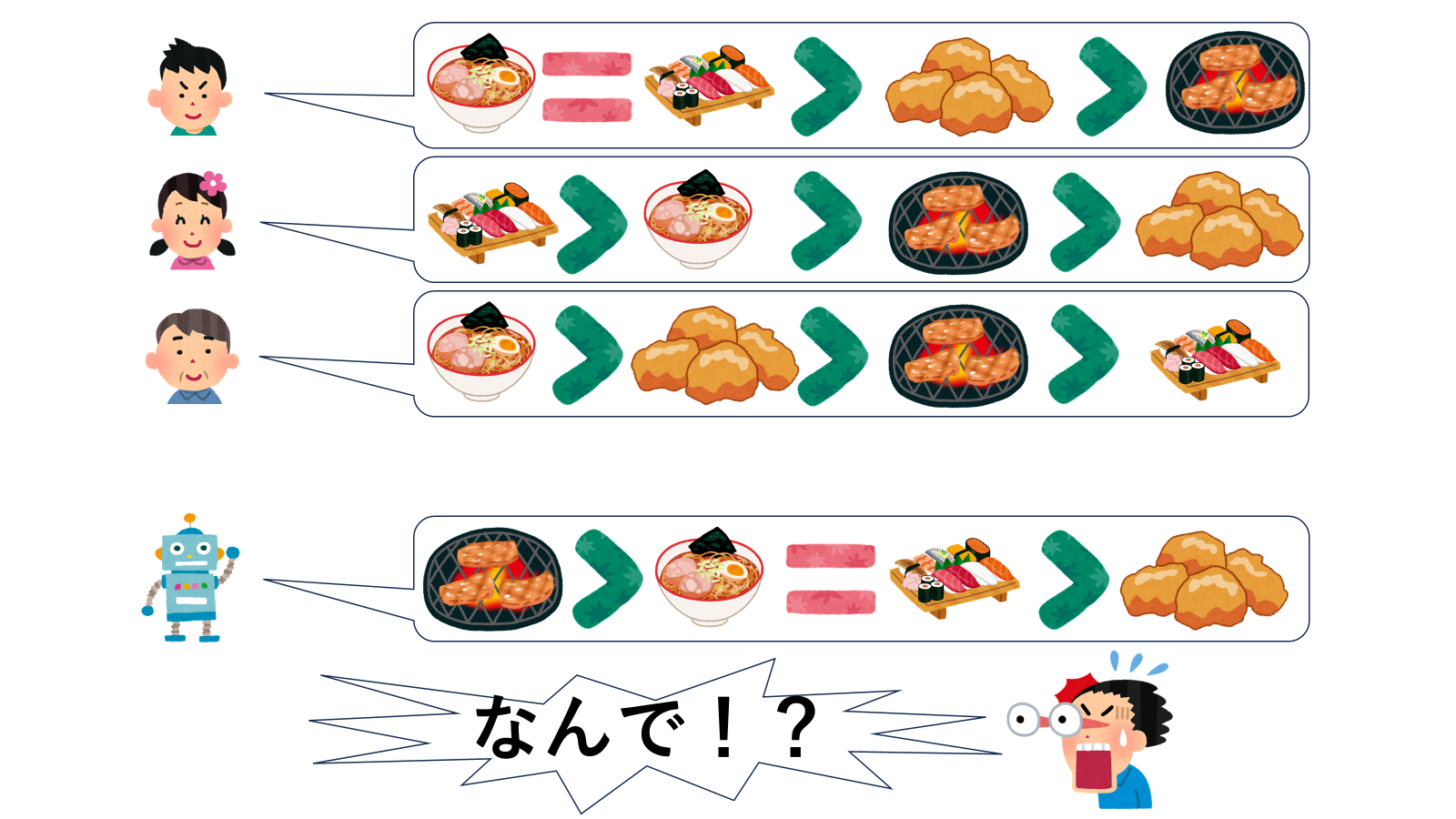
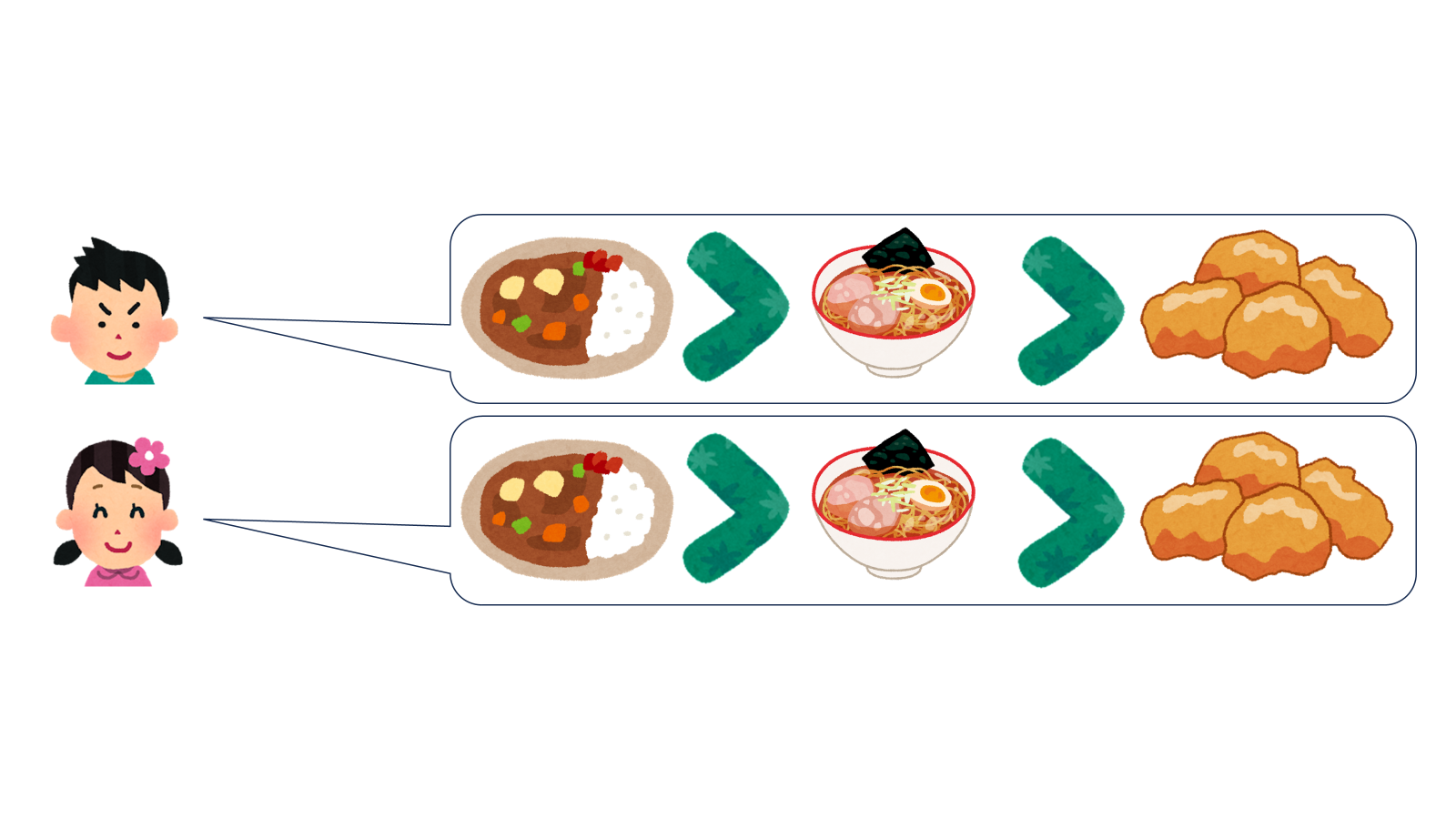
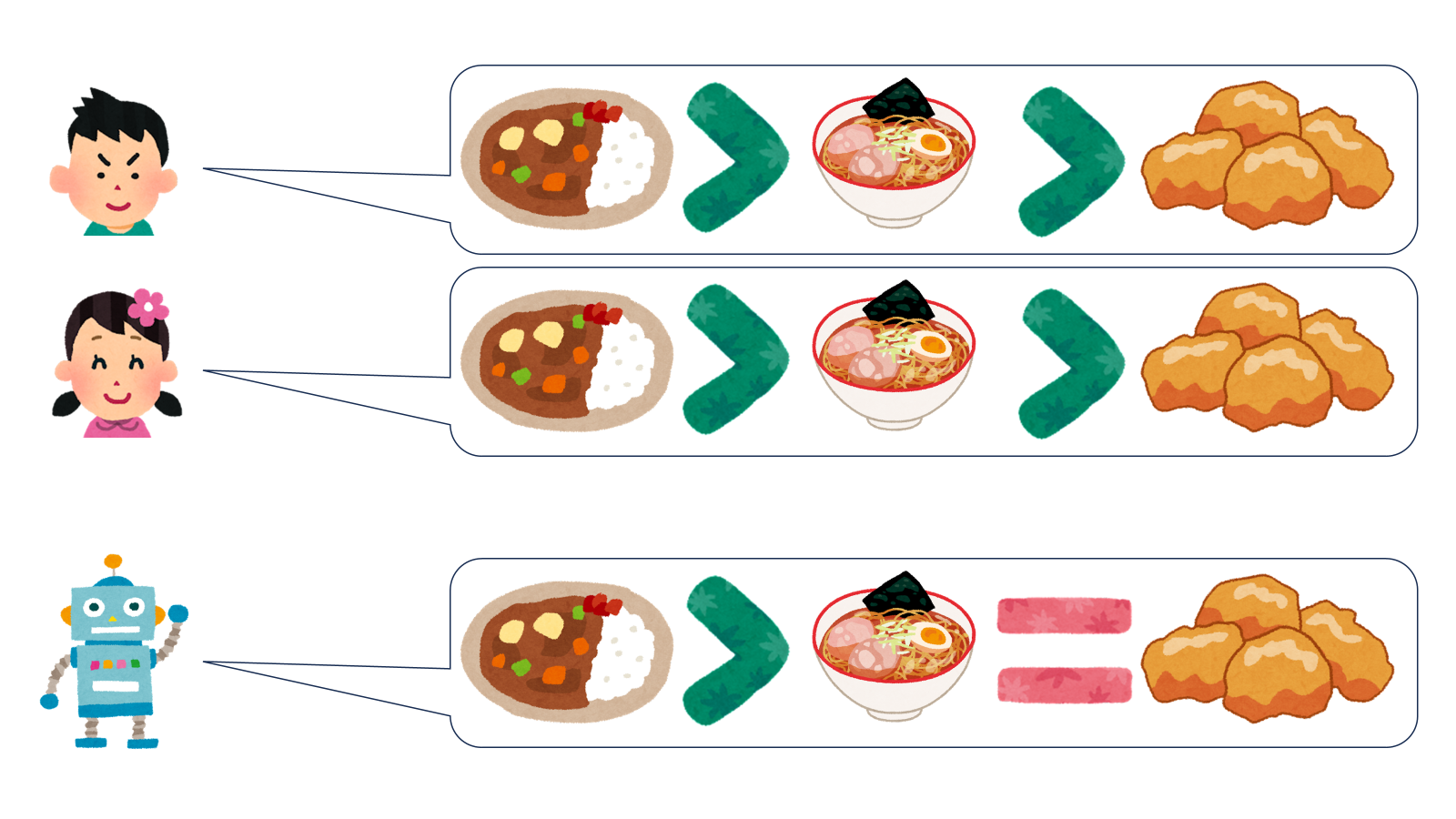
ではここで投票対象が一つ増えて、カレー・ラーメン・からあげの人気を競うことになったとしましょう。各個人の投票は以下のようになっているとします。
では多数決による集計を行います。具体的には、「その食べ物を 1 位に選んだ人数」を比較することにします。すると集計結果はこうなります。
投票者は全員「ラーメンがからあげより好き」だったのに、集計結果ではラーメンとからあげは同率 2 位となっています。したがってこの結果は弱パレート最適ではありません。弱パレート最適であるためにはカレーは 1 位、ラーメンは 2 位、そしてからあげは 2 位ではなく 3 位でなければなりません。
このように選択肢が三つある場合多数決システムではうまくいかないことがあるわけですが、これは多数決に限ったことではありません。一般に「三つ以上の選択肢があるとき、弱パレート最適性・無関係な選択肢からの独立・独裁者の不在の 3 条件を満たす集計方法は存在しない」ことが証明されています。これをアローの不可能性定理といいます。
証明
ここから先はガチガチの数学になるので、興味のない人や途中で分からなくなった人は「おわりに」まで飛ばしてオッケーです。
用語の定義
$X$ を投票対象の集合とします。また投票者は $n$ 人いるものとし、$i$ 番目($1 \leq i \leq n$)の投票者は各々が $X$ 上の全順序関係 $\succsim_i$ を持つものとします。これを $i$ 番目の投票者の選好関係と呼びます。
「全順序ってなんだよ・・・」という方もいると思いますが、これは投票対象 $X$ の要素を一列に並べたものと考えてください。例えばラーメン、お寿司、からあげの三つが投票対象であるとき、1 番目の投票者は「お寿司>からあげ>ラーメン」の順で好きだったとします。この「お寿司>からあげ>ラーメン」が 1 番目の投票者の「選好」$\succsim_1$ と定められます。また今回の選挙では前述の通り「同じくらい好き」という投票も許されるので、「からあげ=お寿司>ラーメン」という選好もアリです。
手前みそになりますが、全順序の厳密な定義は以下の記事を参考にしてください。
ここで、$n$ 人の投票者全員の選好関係を投票順に並べた列 $(\succsim_1, \succsim_2, \ldots \succsim_n)$ から最終的な集計結果である選好関係を出力する関数 $S(\succsim_1, \succsim_2, \ldots, \succsim_n)$ を社会的厚生関数と呼びます。以下、社会的厚生関数 $S$ により定められる最終的な選好関係を $\succsim$ で示します。
次に、decisive coalition というものを定義します。投票順位の集合 $C \subseteq \{1, \ldots, n\}$ があって、以下が成り立つものとします。
$$
\forall i \in C[a \succ_i b] \implies a \succ b
$$
これはつまり「各 $i \in C$ に対し、$i$ 番目の投票者の全員が $a$ を $b$ より好むならば、$S$ による最終的な集計結果でも $a$ は $b$ より上位に来る」ということです。このとき $C$ は「社会的厚生関数 $S$ における $a, b$ に関する decisive coalition」であるというのですが、英語だと覚えにくいのでこの記事では「$a, b$ に関する決定権を持つ集団」と呼ぶことにしましょう。
また、上の decisive coalition の条件を厳しくしたものを weakly decisive coalition といいます。
$$
\forall i \in C[a \succ_i b] \land \color{red}{\forall i \notin C[a \precsim_i b] }\color{black}{\implies a \succ b}
$$
$C$ が weakly decisive coalition に該当するとき、$i(\in C)$ 番目の投票者のみが全員 $a$ を $b$ より好むときに $a \succ b$ が成り立ちます。この記事では weakly decisive coalition を「$a$, $b$ に関する弱い決定権を持つ集団」と呼ぶことにしましょう。
Field Expansion Lemma(拡大補題)
アローの不可能性定理の証明にあたり補題を二つ証明します。一つ目が Field Expansion Lemma とよばれるもので、以下を主張します。
社会的厚生関数 $S$ は弱パレート最適かつ無関係な選択肢から独立であるとする。このとき投票者のとある集団 $C \subseteq \{1, \ldots n\}$ が $S$ において $\exists a, b \in X$ に関する弱い決定権を持つならば、$C$ は投票対象の組すべてに対し決定権を持つ。
なんと、ただ一組の投票対象に対する弱い決定権を持つ集団は投票対象の全ての組に決定権を持つというのです。これが Field Expansion Lemma です。この記事では「拡大補題」とでも呼びましょう。
それでは拡大補題を証明します。まず $x, y$ を任意の投票対象とします。ここで選好関係列 $(\succsim_1, \ldots, \succsim_n)$ を以下が満たされるように適当に定義します。
- $\forall i \in C[x \succ_i y]$
また、これらの選好関係から社会的厚生関数 $S$ により定められる集計結果 $S(\succsim_1, \ldots, \succsim_n)$ を $\succsim$ と置きます。
さらに、もう一つの選好関係列 $(\succsim'_1, \ldots \succsim'_n)$ を以下が満たされるように適当に定義します。
- $\forall i[x \succsim'_i a \land b \succsim'_i y]$
- $\forall i \in C[a \succ'_i b]$
- $\forall i \notin C[a \precsim'_i b]$
- 選好関係 $\succsim_i$ と $\succsim'_i$ が $x$, $y$ に対し定める順序は等しい。すなわち、以下の内ちょうど一つが成立する。
- $x \succ_i y \land x \succ'_i y$
- $x \sim_i y \land x \sim'_i y$
- $x \prec_i y \land x \prec'_i y$
こちらも先ほど同様、$S$ により定められる集計結果を $\succsim'$ と置きます。
まず $S$ が弱パレート最適であることに注意すると以下が成り立つことがわかります。
- $\forall i[x \succsim'_i a]$ ゆえに実際に $x \succsim' a$ である。
- $\forall i[b \succsim'_i y]$ ゆえに実際に $b \succsim' y$ である。
次は $C$ が $S$ において $a$, $b$ に関する弱い決定権を持っていたことに注意します。$C$ に属する投票者のみが全員 $a \succ' b$ を望んでいたので、したがって $a \succ' b$ が実際に成立します。よって先ほど導いた $x \succsim' a$ と $b \succsim' y$ を組み合わせて $x \succsim' a \succ' b \succsim' y$ が成り立つので、$x \succ' y$ が成立します。
加えて、$(\succsim'_1, \ldots, \succsim'_n)$ の定義より各 $i$ に対し $\succsim_i$ と $\succsim'_i$ が $x$, $y$ に対し定める順序は等しいです。よって、社会的厚生関数 $S$ は無関係な選択肢から独立であるという前提条件より、$x \succ y$ が成立します。
ここで $(\succsim_1, \ldots, \succsim_n)$ の定義を思い出してみるとこの選好関係列に課されていた条件は $\forall i \in C[x \succ_i y]$ であることだけでした。ただ一つこれだけの条件から $x \succ y$ が導かれたということは、$C$ は $x$, $y$ に関して決定権を持つ集団であったということです。$x$, $y$ は任意であったので与命題は証明されました。(証明終)
Group Contraction Lemma(縮約補題)
二つ目の補題である Group Contraction Lemma は以下を主張します。
社会的厚生関数 $S$ は弱パレート最適かつ無関係な選択肢から独立であるとする。また投票者のとある集団 $C \subseteq \{1, \ldots n\}$ が $S$ において $\exists a, b \in X$ に関する決定権を持つとする。このとき $C$ は $|C| \geq 2$ である場合に空でない二つの集合 $C_1$ と $C_2$ に分割することができるが、そうすると $C_1$ と $C_2$ のどちらかは投票対象の組のすべてに対し決定権を持つ。
直観的には、ある集団が決定権を持つならばその集団よりもさらに少人数で決定権を持つ集団が存在するみたいな感じです。なのでこの記事では「縮約補題」とでも呼ぶことにしましょう。それでは縮約補題を証明していきます。
まず、$a$, $b$ と異なる第三の投票対象 $c$ を適当に取ってきます。次に選好関係列 $(\succsim_1, \ldots, \succsim_n)$ を以下が満たされるように適当に定義します。
- $\forall i \in C_1[a \succ_i b \land a \succ_i c]$
- $\forall i \in C_2[a \succ_i b \land c \succ_i b]$
また、これらの選好関係から社会的厚生関数 $S$ により定められる集計結果 $S(\succsim_1, \ldots, \succsim_n)$ を $\succsim$ と置きます。
次に二通りに場合分けします。
a ≻ c のとき
先ほど定義した選好関係列 $(\succsim_1, \ldots, \succsim_n)$ の定義より、$a$ と $c$ に関する選好を表明しているのは $C_1$ に属する投票者だけです。これだけの仮定から $a \succ c$ が導かれたということは $C_1$ が $a$ と $c$ に関する決定権を持っていたということにほかなりません。実際、仮定より社会的厚生関数 $S$ は無関係な選択肢から独立なので、$\forall i \in C_1[a \succ_i c]$ が満たされる他のどのような選好関係を集計しても $a \succ c$ が成り立つことが分かります。
a ≾ c のとき
前提条件より $C = C_1 \cup C_2$ は $a$, $b$ に関する決定権を持ち、なおかつ選好関係列 $(\succsim_1, \ldots, \succsim_n)$ の定義より $C_1$ および $C_2$ に属する投票者は全員が $a \succ b$ を望んでいるので、$a \succ b$ が実際に成立します。また前提条件より $a \precsim c$ なので、$c \succ b$ が成立します。よって $a \succ c$ と仮定していたときとおなじ理屈により、$C_2$ は $c$, $b$ に関する決定権を持っていたということになります。
よって $C_1$ と $C_2$ のどちらかはとある組に対し決定権を持つ(したがって当然弱い方の決定権も持つ)ので、拡大補題より $C_1$ と $C_2$ のどちらかは投票対象の組全てに対し決定権を持ちます。(証明終)
ここまでくればアローの不可能性定理まではあと一歩です。まず弱パレート最適の定義を思い出してみましょう。「投票者の全員が $a$ を $b$ より好むならば最終的な集計結果でも $a$ は $b$ より上位に来る」というやつです。このとき、「投票者全員の集合 $\{1, .., n\}$ が任意の $a$, $b$ に対し決定権を持つこと」と「社会的厚生関数 $S$ が弱パレート最適であること」は明らかに同値です。よって、社会的厚生関数 $S$ が弱パレート最適であるならば投票者全員の集合 $\{1, \ldots, n\}$ は投票対象の適当な(というか全ての)組に対し決定権を持つので、縮小補題を繰り返し適用することによって投票対象の任意の組に対し決定権を持つ大きさ 1 の集団が作れてしまいます。これはまさに独裁者にほかなりません。
したがって、社会的厚生関数 $S$ が弱パレート最適かつ無関係な選択肢から独立であるならば $S$ は独裁的です。言い換えれば、弱パレート最適かつ無関係な選択肢から独立かつ非独裁的な社会的厚生関数は存在しません。(証明終)
おわりに
ここまでギチギチの数学的議論により証明されたように、アローの不可能性定理はただ数学の世界における帰結にすぎません。ですからこの定理が現実世界についてどういう意味を持つかについては慎重に考える必要があります。
例えばあの有名な「ゲーデルの不完全性定理」なんかも、「不完全性定理ゆえに神は存在しない」だとか「不完全性定理ゆえに論理は本質的に不完全だ」だとか勝手なことばかり言われています。しかし不完全性定理は純粋に数学的な帰結にすぎないので、神の存在性だとか論理の完全性だとかとは無関係です。
アローの不可能性定理に関しても、「アローの不可能性定理ゆえに唯一正しい政治体制とは独裁制である」とか「民主主義は本質的に不可能である」とかいった政治的主張の根拠に使われてしまうことがあります。しかしアローの不可能性定理の適用範囲外であるような選挙方法はいくらでもあるので、アローの不可能性定理を性急に現実世界に結びつけるべきではありません。
これはあくまでも個人的な所見ですが、私としては「無関係な選択肢からの独立」という前提条件が強すぎるように思えます。例えば投票対象の食べ物がお寿司と唐揚げの二択で、それぞれ 30 票と 50 票集めたとしましょう。魚よりもお肉の方が好きだから唐揚げに投票した人の方が多かった構図になります。しかしここで第三の選択肢としてザンギが追加されたとしましょう。すると、魚よりもお肉が好きな人は唐揚げとザンギのどちらかに投票するでしょうから、結局唐揚げとザンギで票を奪い合う形になります。最終的にお寿司、唐揚げ、ザンギで票数が 30, 25, 25 とでもなったとすると、国民の過半数はお肉が好きであるのにもかかわらず、なぜかお寿司が当選することになります。またそれ以上に、「ザンギ」という選択肢が追加されたことによって「お寿司」と「唐揚げ」の順位が入れ替わってしまっています。つまりこのケースでは「無関係な選択肢からの独立」が成り立っていないのです。結局のところ「無関係な選択肢からの独立」という前提条件は、一見すると妥当なように見えて実は全然現実に即していないのです。
最後にアローの不可能性定理の証明者である経済学者ケネス・J・アローの言葉を引用して終わりにさせていただきます。
(前略)
原文:"Most systems are not going to work badly all of the time,"
拙訳:ほとんどのシステムは、常にうまくいかない訳ではない。(中略)
"All I proved is that all can work badly at times."
私が証明したのは、どんなものも時にはうまくいかない場合があるということである。(後略)
出典:Phil McKenna. Vote of no confidence. New Scientist, Vol. 198, Issue 2651, pp. 30-33, 2008.
参照元:RangeVoting.org, https://rangevoting.org/McKennaText.txt, 2024/4/14 アクセス.
お読みいただきありがとうございました。
参考