TL; DR
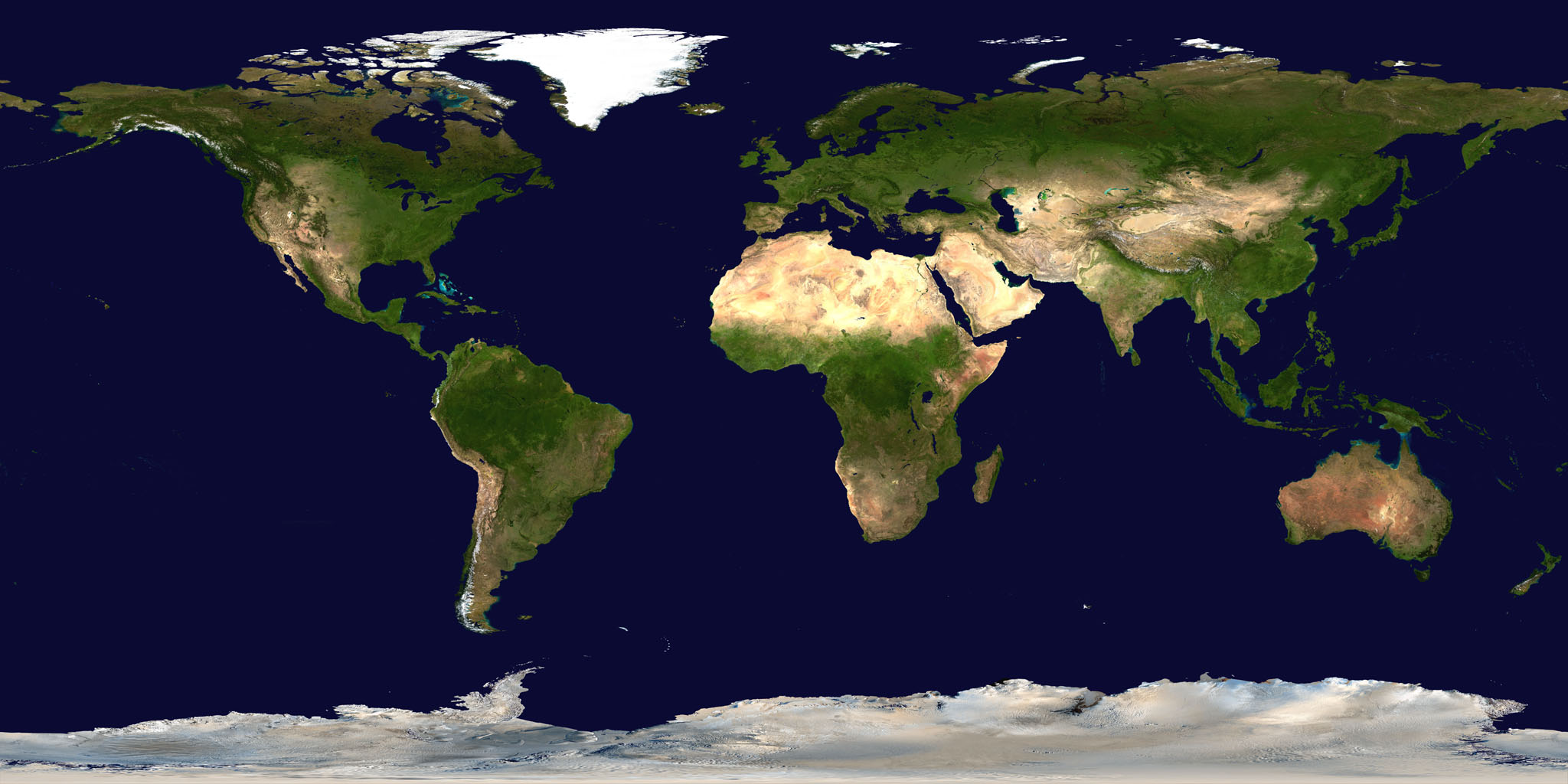
我々がふだん目にする世界地図はこのくらい歪んでいます。
 |
 |
|---|---|
| よく見かける世界地図 | そのおそるべき実態 |
世界地図の作り方
「地図」は我々の日常にありふれたものです。しかし地図を作るのって意外と大変です。我々は地球という「球」の上に住んでいるわけですが、これを地図という「平たい紙」に書き写すといろいろな不具合が生じます。具体的にはこんな感じです。
- 地形が激しく歪む!
- 面積が狂う!
- 地球上での最短経路が地図上では最短経路にならない!
- 地点間の角度がめちゃくちゃになる!
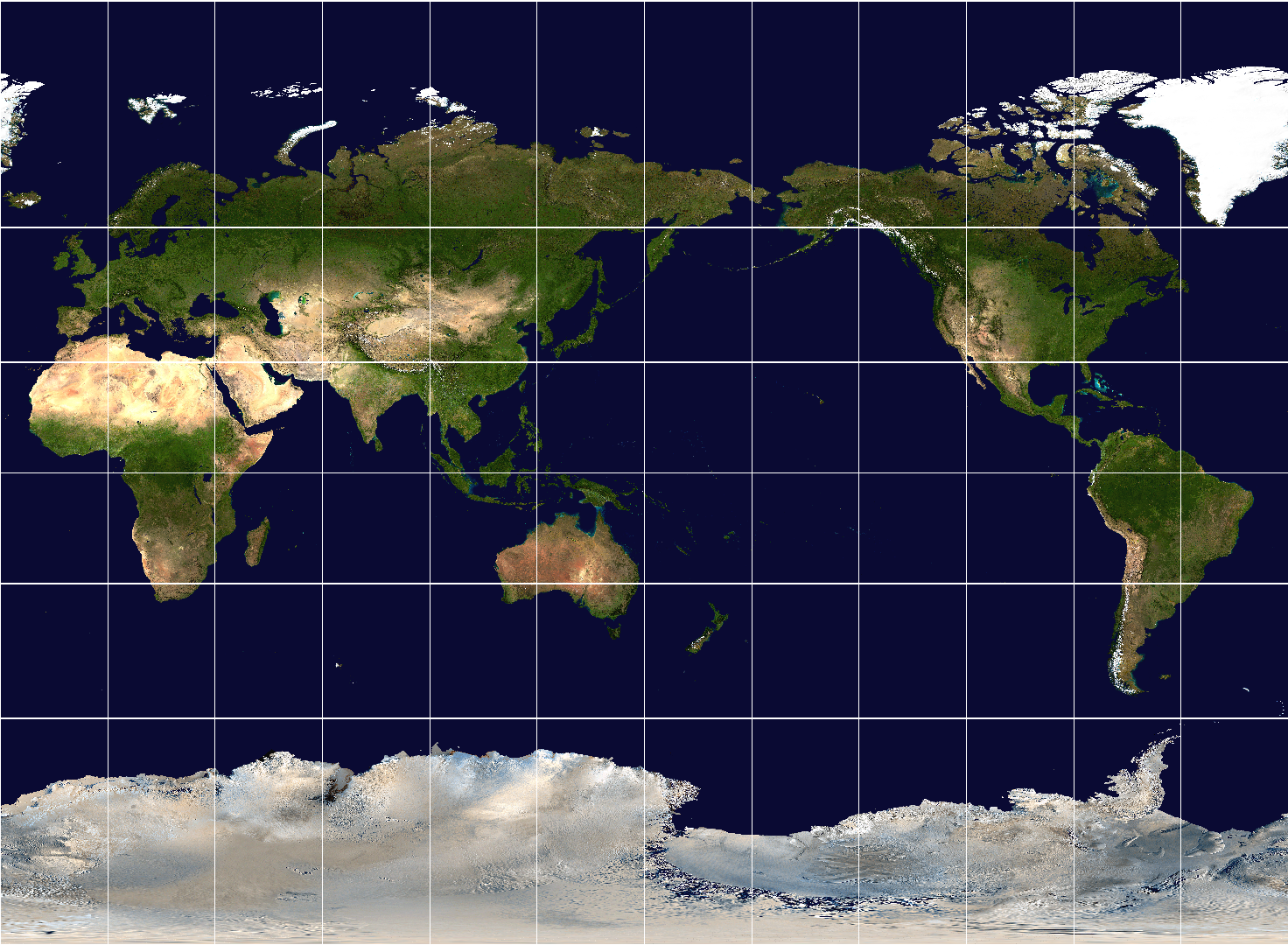
地図には様々な種類があり、それぞれが一長一短です。そんな中でも、ミラー図法というのが大多数の方が想像する「いわゆる世界地図」になると思います。
 |
|---|
| 自作のプログラムで加工したミラー図法地図(加工元データの出典:NASA) |
本題に入る前にこのミラー図法の作り方について説明します。
正距円筒図法
地球上の一地点は緯度・経度によって指定されます。たとえば東京タワーはおおむね北緯 35 度、東経 139 度の位置にあります。
ところで地理情報を数学的に取り扱うときには緯度・経度をそれぞれ $\phi$, $\lambda$ と置くそうです。緯度は北向きを正、経度は東向きを正とするのが一般的なようです。よって東京タワーの座標はざっくりと $(\phi, \lambda) = (35^\circ, 139^\circ)$ と表せます。
さてこの一方で地図は平面ですから、$x$ 座標と $y$ 座標で位置があらわされます。つまり地図を作るには緯度・経度から $x$ 座標・$y$ 座標への変換が必要になるのです。
ここで説明する正距円筒図法は実に単純明快な変換を用います。1
\left\{
\begin{array}{ll}
x = \lambda \\
y = \phi
\end{array}
\right.
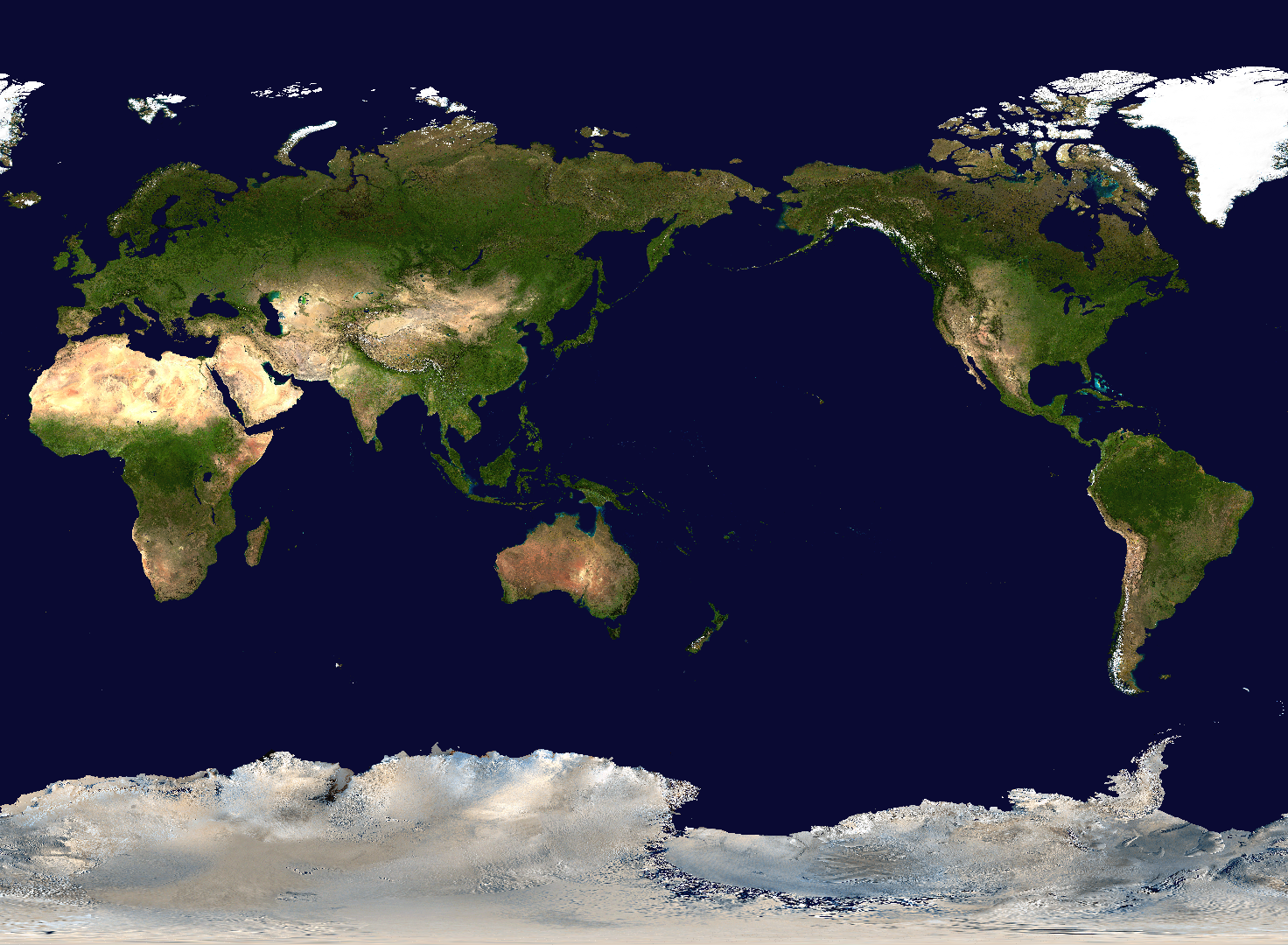
正距円筒図法の地図はこんな感じです。
 |
|---|
| 正距円筒図法地図(出典:NASA) |
見慣れた世界地図に比べるとアメリカの方がつぶれてますね。この地図は赤道上、もしくは経線上において距離関係が正しく保たれています。その代わり面積や角度は狂っています。
メルカトル図法
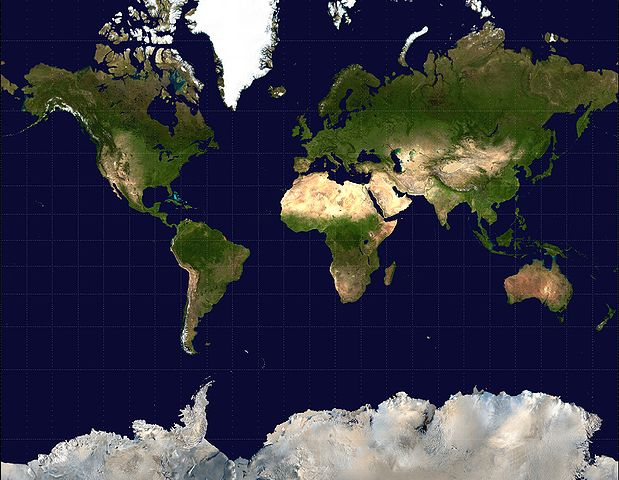
正距円筒図法の地図を「逆グーデルマン関数」というものを使って縦方向に引き伸ばしたものをメルカトル図法といいます。
\left\{
\begin{array}{ll}
x = \lambda \\
y = \mathrm{gd}^{-1}(\phi)
\end{array}
\right.
 |
 |
|---|---|
| メルカトル図法地図(パブリックドメイン) | 逆グーデルマン関数(パブリックドメイン) |
縦に伸ばすことのメリットですが、メルカトル図法の地図上での直線は等角航路になります。メルカトル図法地図において出発地と目的地を結ぶ直線と経線の角度(舵角)を測り、あとはコンパスを頼りにひたすら舵角の方へ進んでいけば目的地に着きます。つまりメルカトル図法地図は海図にとても向いていたのです。
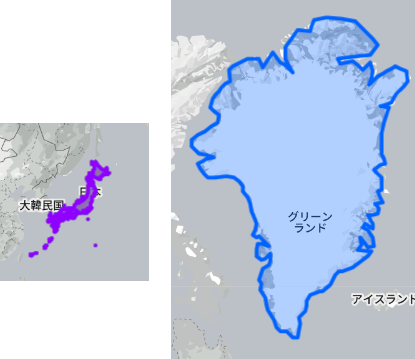
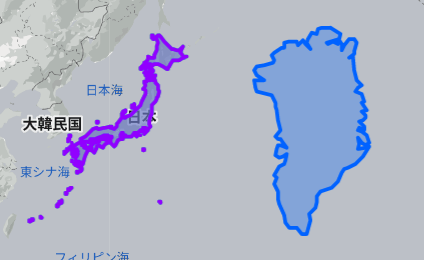
ただしメルカトル図法地図には見過ごせない欠点もあります。一つ目は地図の上と下の方で面積が激しく歪むということです。例えばグリーンランドなんかは超巨大に描かれてしまっていますが、実際には大した大きさではありません。
 |
 |
|---|---|
| メルカトル図法地図上での日本とグリーンランド(出典:The True Size Of ...) | 概ね正しい面積比(出典:同左) |
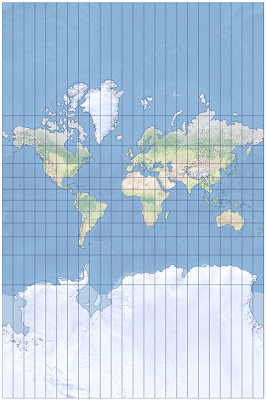
もう一つの欠点ですが、用途次第ではこれが致命的です。メルカトル図法の地図においては、地球全域を描くのに無限の面積が必要になってしまうのです。なので巷で見かけるメルカトル図法の地図は実は北端の方と南端の方を切り取っています。切り取らないとこんな感じになってしまいます。
 |
|---|
| 南極がデカすぎるメルカトル図法地図(出典:esri) |
ミラー図法
メルカトル図法の地図は面積が無限になってしまう欠点がありましたが、メルカトル図法の計算式をちょっといじくることでこれを回避したのがミラー図法です。
\left\{
\begin{array}{ll}
x = \lambda \\
y = \frac{5}{4}\mathrm{gd}^{-1}\left(\frac{4}{5}\phi\right)
\end{array}
\right.
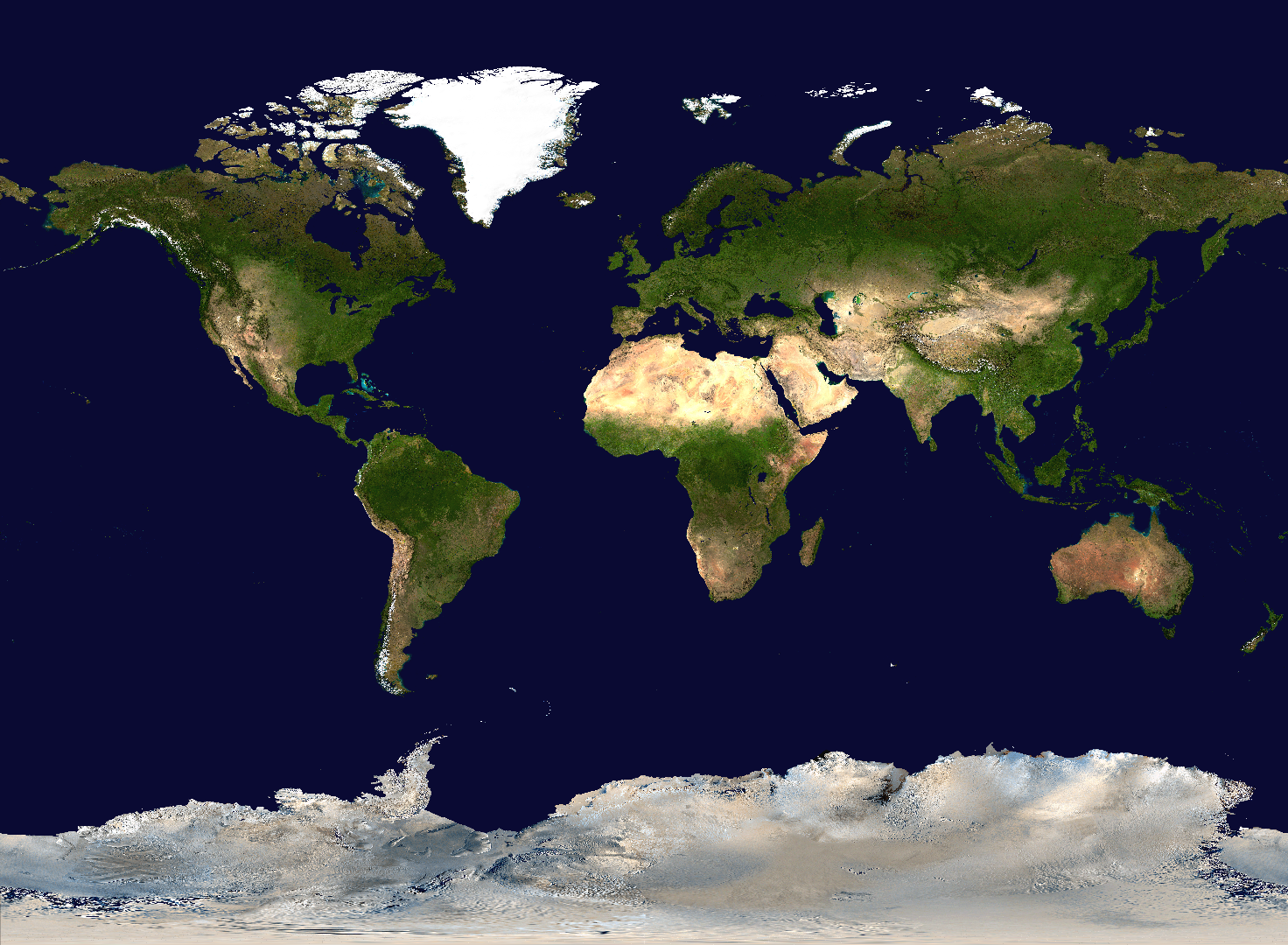 |
|---|
| 自作のプログラムで加工したミラー図法地図(加工元データの出典:NASA) |
正距円筒図法のように潰れてもいませんし、メルカトル図法のように面積が無限になることもないので見やすい世界地図になっています。その代わり正距円筒図法と違って距離は狂っていますし、メルカトル図法とも違って角度も狂っています。ついでに面積も狂っています。ぶっちゃけ「見やすい」こと以外の実用性はありません
本題
この記事の目的は我々が普段目にする世界地図、すなわちミラー図法の地図の歪みを分かりやすく実感したいというものでした。そこで、地球をぐるぐる回すことで、ミラー図法地図がどのように変化するかを動画形式でお見せしたいと思います。
動画の作成に使用した地図画像は NASA のサイトから一番解像度が高いやつをもらいました。画像データなのに 600 メガバイト以上あります。
また動画の作成に利用したプログラムのソースコードはこちらになります。
画像処理にも動画の書き出しにも OpenCV が使えました。しかも並列計算もできるので爆速です。便利ですね~。
ヨー
まずはヨー($z$ 軸周りの回転)からです。ちなみに以下の動画は無駄に 1080p 60fps です。
・・・まあ、これに関しては「うん、だろうね」って感じの結果だと思います。次からが本番です。
ピッチ
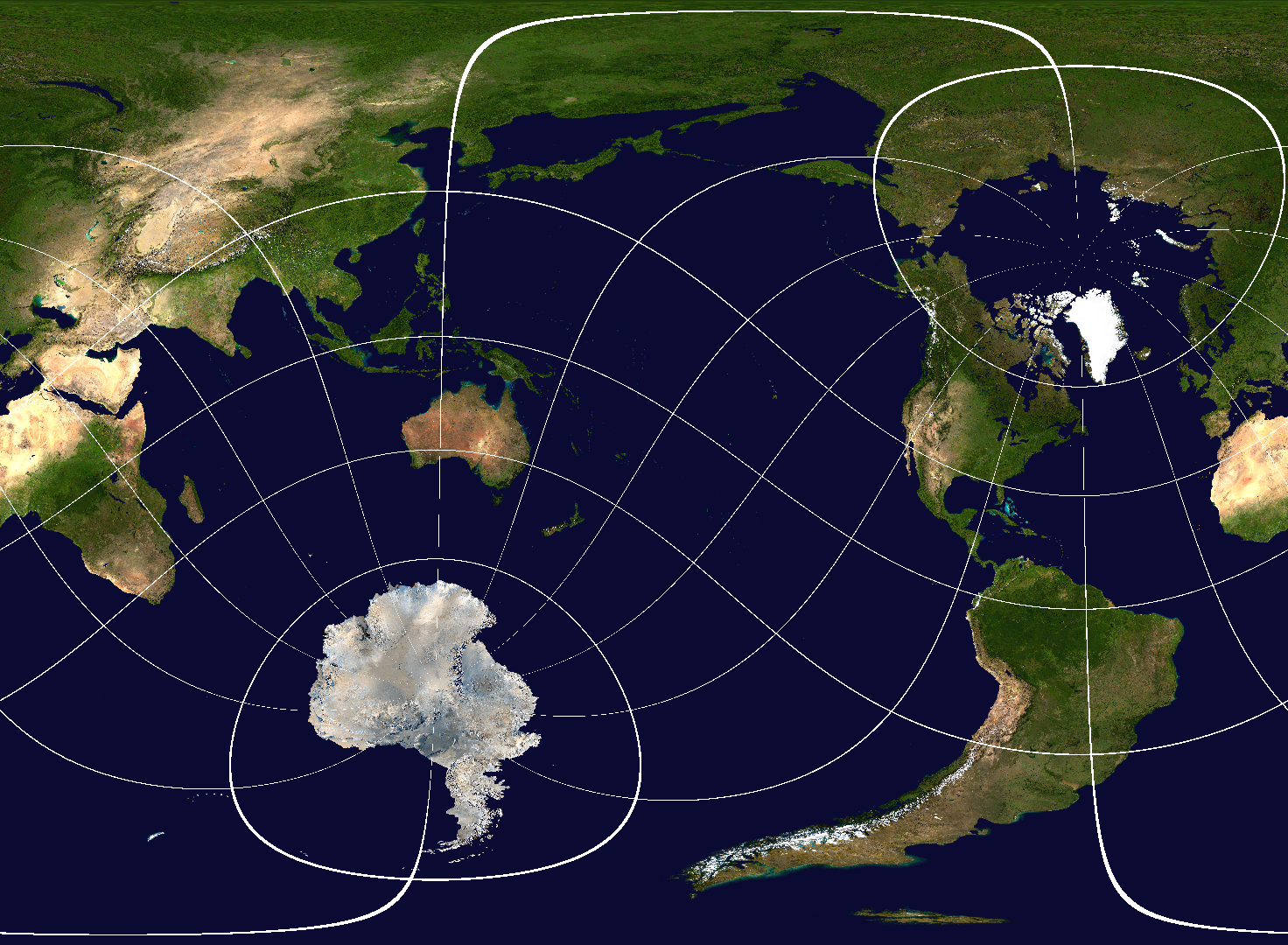
お次はピッチ($y$ 軸周りの回転)です。
ぐにゃんぐにゃんになっています。また先ほども述べたように、地図の上の方と下の方で激しく歪んでいるのがわかると思います。
ロール
最後にロール($x$ 軸周りの回転)です。
こちらもぐにゃぐにゃです。やっぱり上の方と下の方で激しく歪んでいます。
