ほんとうに「ゼロから」理解する P ≠ NP 問題

はじめに

みなさん、1 億 4000 万円欲しくないですか？（挨拶）

「ミレニアム懸賞問題」というものをご存じでしょうか。クレイ数学研究所によって懸賞金がかけられた、七つの怪物級数学問題です。このそれぞれに 100 万ドル、昨今の日本円にして 1 億 4000 万円の懸賞金がかけられています。ただでさえ天才たちのひしめく数学界ですがミレニアム懸賞問題は「キノコ狩りの数学者」グレゴリー・ペレルマンによってポアンカレ予想が解決されたのみで、残りの六つは未だ謎に包まれています。

そんな未解決ミレニアム懸賞問題の一つが P ≠ NP 問題です。数学者によって懸賞金をかけられた問題といえど、この問題は Qiita に集う我々エンジニアにとっても他人事とはいえぬ大問題です。

• もし P = NP である場合
  • 解くのにものすごく時間がかかる問題を一瞬で解く方法が見つかるかもしれません。
  • しかし裏を返せば暗号を一瞬で突破する方法などが見つかってしまい、世界が大混乱に陥るかもしれません。
• もし P ≠ NP である場合
  • 暗号がそう簡単に破られることはありません。むしろ「簡単には突破されない」という保証が手に入ります。
  • しかし解くのに時間がかかる問題は解くのに時間がかかるままです。希望は潰えました。

この記事が目指すことは、計算理論の専門知識を一切持たない方にも P ≠ NP 問題の厳密なステートメントを理解していただくことです。P ≠ NP 問題が解けたら 1 億円もらって 🔥FIRE🔥 しましょう。

宣伝

お話に入る前に今回の話題についておすすめの本のご紹介です。川添愛先生の白と黒のとびら / 精霊の箱です。気難しい魔術師に弟子入りした主人公の少年が成長していくファンタジー小説の体裁をとりながら、計算理論について楽しく、面白く、熱く学ぶことができます。ぜひおすすめの 1 冊です。

それでは本題に入っていきましょう。

第 1 部：入門・計算理論

P ≠ NP 問題は計算理論と呼ばれる学問分野の問題です。個人的にこの計算理論というのはとてもエキサイティングな分野だと思うので、楽しみながら学んでいきましょう。計算理論が解き明かしたいことは主に以下の通りです。

• どのようにして問題を解くか？
• ある問題を解くのはどれくらい難しいことなのか？
• 解ける問題と解けない問題の違いは何なのか？
• etc. ...

要は「問題を解くこと」を取り扱う学問が計算理論です。またここでいう「問題」は数学的な問題に限りません。例えば、

• $2 \times (3 + 4)$ はいくつか？
• 3127 は素数か否か？
• 文字列 "abcba" は回文になっているか否か？
• この図形は一筆書き可能か否か？
• セールスマンがすべての都市を回るのには最短でどれだけの時間がかかるか？
• etc. ...

などレパートリーに富んでいます。

ところでこれらの問題は決定問題と関数問題に分けることができます。決定問題とははい・いいえで答えられる問題のことで、それ以外の問題が関数問題です。上に挙げていた例の中では以下が決定問題にあたります。

• 3127 は素数か否か？
• 文字列 "abcba" は回文になっているか否か？
• この図形は一筆書き可能か否か？

一方、以下は関数問題です。

• $2 \times (3 + 4)$ はいくつか？
• セールスマンがすべての都市を回るのには最短でどれだけの時間がかかるか？

先に言っておくと P ≠ NP 問題は決定問題にかかわる問題です。なのでここから先は決定問題を「如何にして解くか」を考えていきます。

如何にして決定問題を解くか

先ほど決定問題の例として三つ挙げました。

• 3127 は素数か否か？
• 文字列 "abcba" は回文になっているか否か？
• この図形は一筆書き可能か否か？

1 問目は電卓で頑張れば解けますし、2 問目と 3 問目は紙とペンで頑張れば解けそうです。しかし計算理論が実際に取り扱うべき決定問題はこの三つの他にも無数にあります。そのそれぞれに対し、電卓が必要そうだから電卓を取ってくる、紙とペンが必要そうだから紙とペンを取ってくるなんてやってたら日が暮れてしまいます。そこでこういった問題に汎用的に対応できる神ツールを作ってしまいます。

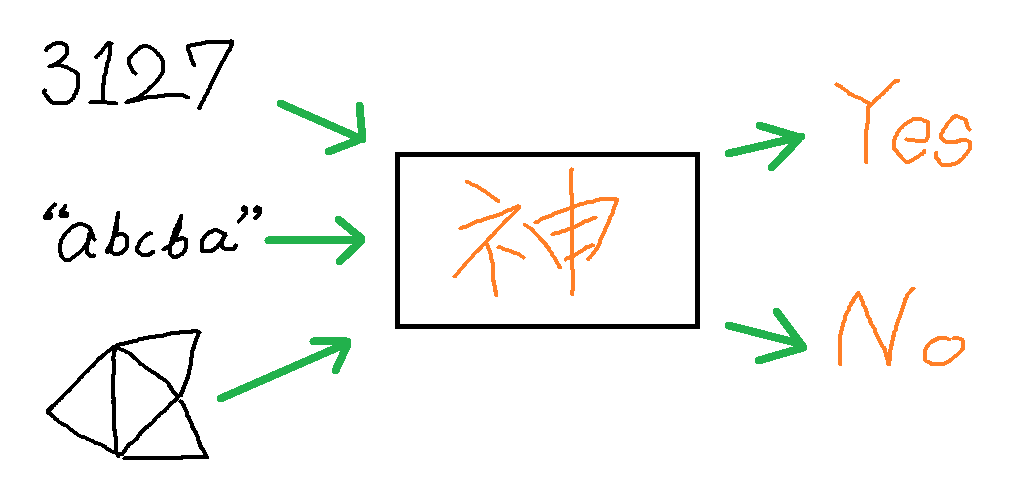
しかし「神ツール」の実現までにはいくつもの壁があります。最初に問題となるのは入力の形式の問題です。

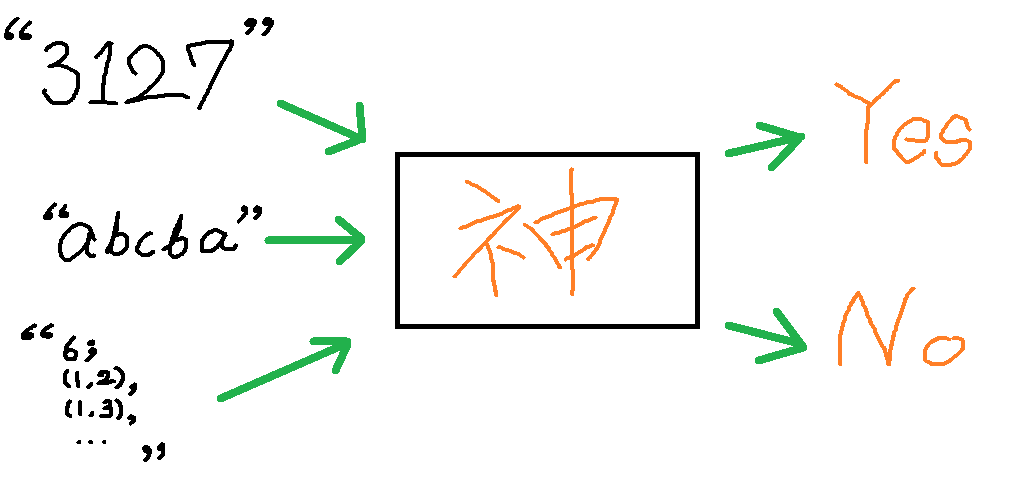
ご覧の通り「神ツール」はあるときは自然数、あるときは文字列、またあるときは図形と、形のあるものから形のないものまでなんでもかんでも入力されてしまいます。さすがにそれでは取り付く島もないので、「神ツール」への入力形式を統一します。具体的にはこんな感じです。

このように「神ツール」へは文字列を渡すことにします。数は適当な進法で表記すれば文字列になりますし、グラフだって頑張れば文字列で表現できます。よって、「神ツール」は受け取った文字列に応じて Yes / No を適切に回答する仕組みであってほしいわけです。そんな都合のいいもの作れるでしょうか？

「神ツール」バージョン 1：有限オートマトン

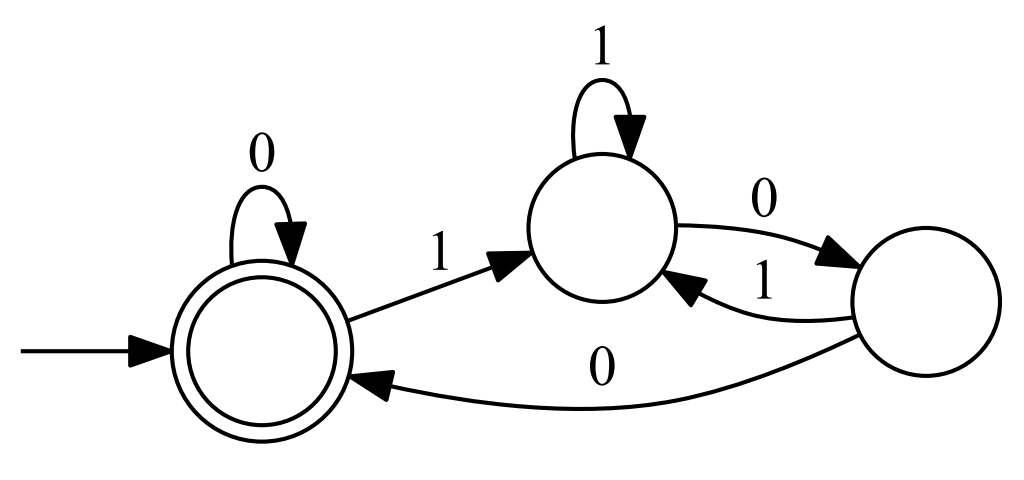
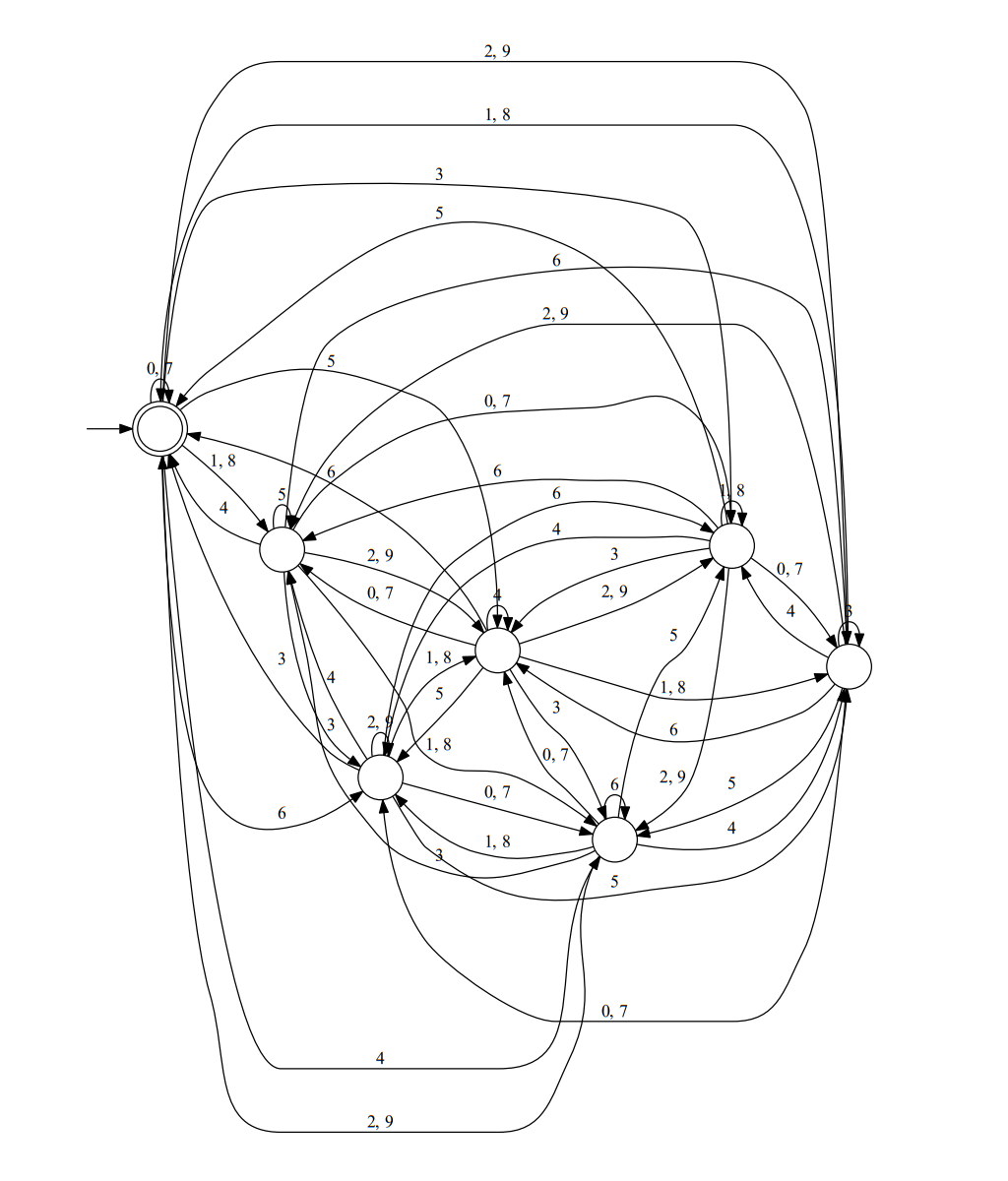
「受け取った文字列に応じて Yes / No を適切に回答する仕組み」として最も単純なものが有限オートマトンです。これは実物を見るのが一番手っ取り早いでしょう。

厳密な定義は後回しにして、ひとまずはこれの「使い方」を説明します。まず有限オートマトンの「スタート地点」を探します。

このように丸と繋がっていない矢印から指されている丸が一つあるはずなので、そこからスタートします。

上の図では少し勘違いしやすくなってしまっているかもしれませんが、「丸と繋がっていない矢印から指されていること」がスタート地点であることの合図です。二重丸であることはすぐ後で述べる別の意味を持っています。

次に、入力となる文字列を先頭から 1 文字ずつ順番に見ていき、それに対応した矢印を通って移動していきます。そして最終的にたどり着いた丸が二重丸だったら回答は Yes、そうじゃなかったら No ということになります。ぜひ実際に確かめてみてほしいのですが、例えば "0101100" とかの場合は二重丸にたどり着くはずなので答えは Yes となります。

有限オートマトンのちゃんとした定義

有限オートマトン $A$ は五つ組 $\langle \Sigma, Q, q_{\mathrm{init}}, F, \delta \rangle$ です。それぞれ以下のように定められます。

• $\Sigma$（入力字母）：有限集合（空でもよい）。またこの元を入力記号という。
• $Q$（状態集合）：空でない有限集合。またこの元を状態という。
• $q_{\mathrm{init}}$（初期状態）：$Q$ のとある元。
• $F$（受理状態集合）：$Q$ のとある部分集合。空でもよい。またこの元を受理状態という。
• $\delta$（遷移関数）：$\Sigma \times Q$ から $Q$ への写像。

$A$ に文字列 $\sigma_1\sigma_2\cdots\sigma_n$（各 $\sigma$ は $\Sigma$ の元）が入力されたとき、以下の漸化式によって状態の列を定めます。

\left\{
  \begin{align*}
    q_0 &= q_{\mathrm{init}} \\
    q_{i+1} &= \delta(\sigma_{i+1}, q_i)
  \end{align*}
\right.

このようにして定められる最後の状態 $q_{n}$ が $F$ の元であったならば $A$ は入力を受理したといい、これは回答が Yes であるという意味です。またそうでなかった場合 $A$ は入力を拒否したといい、これは回答が No であるという意味です。

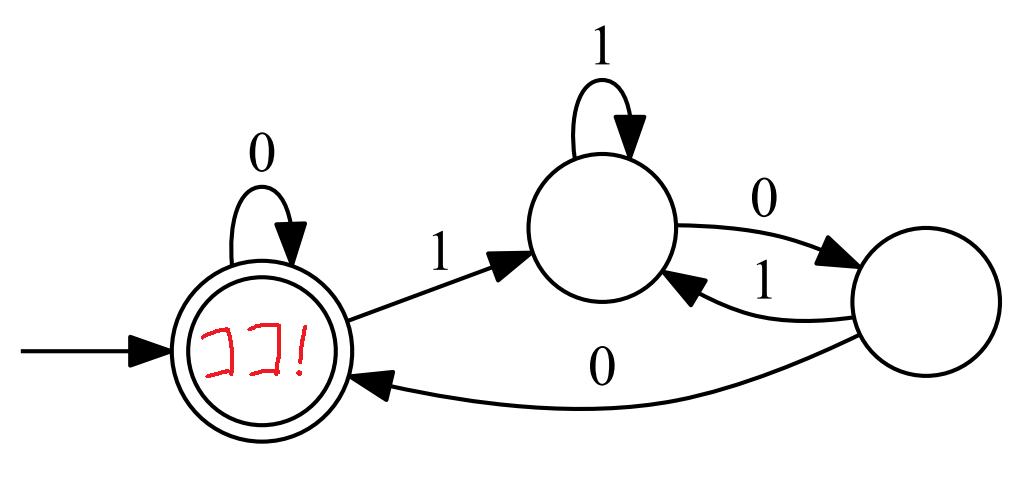
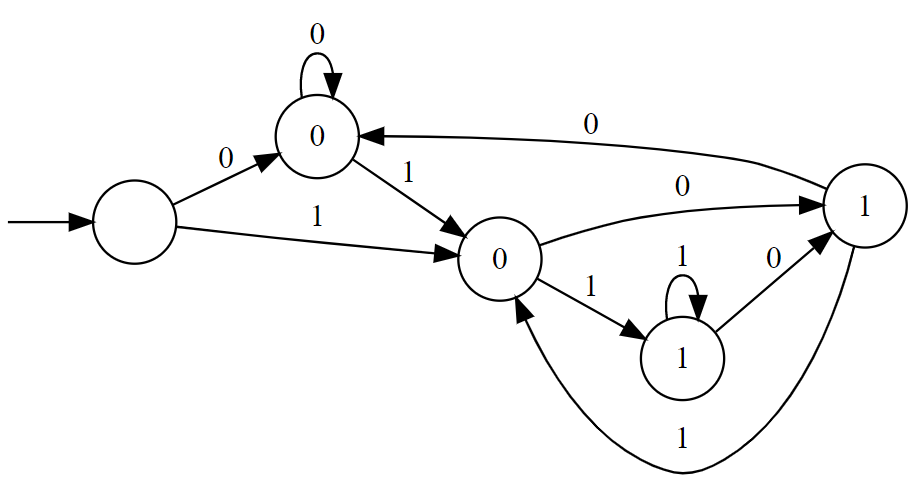
さてこの通り有限オートマトンは単純極まりない仕組みなので、読者の皆様にはほんとにこんなものでまともな問題が解けるの？​とお疑いの方もいるでしょう。そこで先ほどの有限オートマトンをもう一度見てみましょう。

この有限オートマトンですが、よく見てみると「"0" が 1 文字のみの文字列、もしくは最後の 2 文字が "00" である文字列」に Yes と回答することがわかります。つまりこの有限オートマトンは二進表記された自然数を入力として受け取り、その数が 4 の倍数であるか否か回答できるのです（！！！）

ただしスタート地点がいきなり二重丸でもあるため、厳密には後でも出てくる「空の文字列」に対しても Yes と回答してしまいます。N 進表記の定義からして「空の文字列」は "0" という数に対応しているとみなした方が見通しが良くスッキリした設計になるのでこのような有限オートマトンになっているのですが、「空の文字列に対しては No と回答する」という動作にすることももちろん可能です。

これだけでは地味すぎますが、頑張れば「十進表記された自然数を受け取り、その数が 7 の倍数であるか判定する」などということもできます。下図は自作のプログラムで自動生成したものなのでかなり見辛いですが・・・

今回は有限オートマトンを決定問題を解くためのツールとしてご紹介しましたが、ちょっと改造してやることで関数問題に回答させることもできます。代表例としてはムーアマシンとミーリマシンがあります。

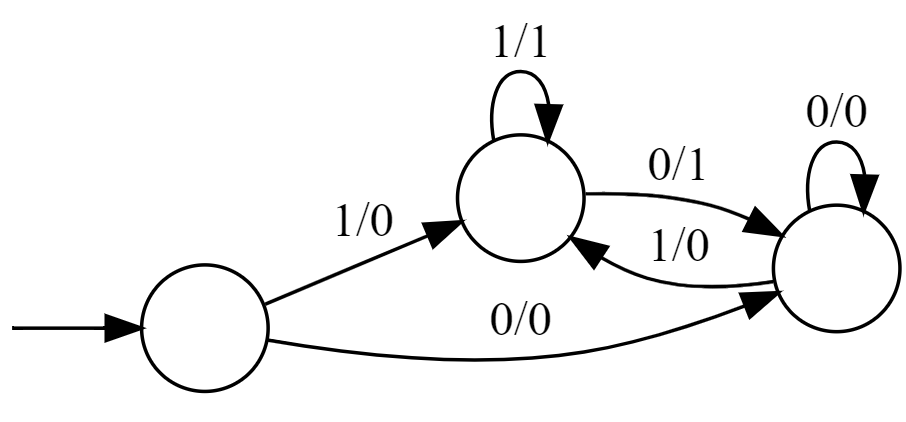
下図はムーアマシンとミーリマシンそれぞれによる遅延回路の実装です。すなわち入力されたバイナリ列 $b_0b_1b_2\cdots$ に対し $0b_0b_1b_2\cdots$ を順次出力していきます。下図左のムーアマシンは遷移先の状態に応じて文字を 1 文字出力します。"0" と書かれた状態にたどり着いた時には "0" を、"1" と書かれた状態にたどり着いたときは "1" を出力します。それに対し下図右のミーリマシンは受け取った文字と遷移先に応じて文字を 1 文字出力します。それぞれの矢印に振られた "x / y" というラベルは「文字 x を読み取って遷移を行い、文字 y を出力する」という意味です。

ムーアマシンによる遅延回路	ミーリマシンによる遅延回路

ではこの有限オートマトンは本当にどんな問題にも対応できる「神ツール」なのでしょうか？

有限オートマトンの限界

「まあ、だろうね」という感じでしょうが、残念ながら有限オートマトンでは解けない問題がいっぱいあります。その代表例が回文判定です。きちんとした証明には「反復補題」というものを使うのですが、入力された文字列が回文であるか、すなわち前から読んでも後ろから読んでも同じ文字列になるかは有限オートマトンでは判定できません。では有限オートマトンで解ける問題と解けない問題は何が違うのでしょうか？

ここで一旦話を整理するためにちゃんとした専門用語をいくつか持ってきます。少しイカツく見えるかもしれませんが、難しい話をしているわけではないので気負わず行きましょう。

さて我々が作りたい「神ツール」ですが、これは「入力された文字列に応じて Yes / No を適切に回答する装置」でした。言い換えると「入力された文字列が所与の条件を満たしているか判定する装置」といえます。

ここで専門用語その 1 です。計算理論では、所与の条件を満たす文字列の集合を形式言語、または単に言語といいます。例えば以下は全て「言語」です。

• 全ての 4 の倍数を二進表記したものの集合
• 回文の集合
• 文法的に問題のない C 言語ソースコードの集合

また「言語」の元を語といいます。例えば "aabbaa" という文字列は「回文言語」の「語」ですが、"Qiita" は「回文言語」の「語」ではありません。

この専門用語を用いて記述すると、「神ツール」とは「入力された文字列が所与の言語の語であるか判定する装置」であるといえます。

さて、上で見たように「4 の倍数言語」は有限オートマトンで取り扱える言語でしたが、残念ながら「回文言語」は有限オートマトンで取り扱える言語ではありませんでした。それでは有限オートマトンはどんな言語なら取り扱えるのでしょうか？

正規文法

突然ですが、「4 の倍数言語」はこのように記述することができます。

\begin{align*}
  S &\rightarrow A0 \\
  S &\rightarrow \varepsilon \\
  A &\rightarrow B0 \\
  A &\rightarrow \varepsilon \\
  B &\rightarrow B0 \\
  B &\rightarrow B1 \\
  B &\rightarrow \varepsilon
\end{align*}

なんのこっちゃ！？​とお思いでしょうが、一歩ずつ見ていきましょう。

先ほど「言語」とは「所与の条件を満たす文字列の集合」であると話しましたが、その「条件を満たす文字列」の作り方を教えてくれるものを生成文法といいます。

「生成文法」という概念は言語学で考案されたものを計算理論に応用したものなので、「生成文法」という専門用語自体は計算理論独自のものではありません。

上に出したわけのわからない表ですが、この表の各行は「矢印の左側の記号を右側の記号に書き換えてもよい」という意味を持っています。

最初の行の $S$ に着目しましょう。実は $S$ というのは Start の略です。なのでここから始めます。1 行目には「$S$ は $A0$ に書き換えてもよい」と書かれていますね。

さらに 4 行目には「$A$ を $\varepsilon$ に書き換えてもよい」と書いてあります。$\varepsilon$ ってなんやねんって話ですが、この記号は空文字列という意味です。要するに C 言語などのプログラミング言語における "" です。さっき $S$ を書き換えて手に入った $A0$ の $A$ を空文字列に書き換えれば文字列 "0" が手に入ります。これはまぎれもなく 4 の倍数ですね！

このように上の規則に従って $S$ から文をどんどん書き換えていけばどんな 4 の倍数でも手に入ります。逆に 4 の倍数でない数はどうあがいても手に入りません。例えば "0010111" などは絶対に作り出せません。

さて、実は上の表において大文字アルファベットは「いずれ書き換えられなければならない記号」という意味を持たされています。専門的には「非終端記号」といいます。非終端記号以外は「終端記号」といい、最終的に得られる文を構成する文字たちに当たります。今回は 0 と 1 のことですね。そして生成文法のうち、

• <非終端記号> → $\varepsilon$
• <非終端記号> → <終端記号>
• <非終端記号> → <非終端記号><終端記号>

という書き換えルールのみを持つものを左正規文法といいます。最後のルールは「<非終端記号> → <終端記号><非終端記号>」でもよく、この場合は右正規文法といいます。といっても両者の表現能力は全く同じなので、本質的な違いはありません。この二つを合わせて正規文法といいます。また、正規文法によって記述できる言語を正規言語といいます。

さて有限オートマトンをほったらかしにしていきなり何を言っているんだという話ですが、有限オートマトンと正規言語には切っても切れない関係があります。証明は略しますが、ある言語が有限オートマトンで取り扱える必要十分条件はその言語が正規言語であることです。

要するに「4 の倍数言語」と「回文言語」の違いは、正規言語であるか正規言語でないかということだったのです。有限オートマトンにはかわいそうですが回文判定もできないようでは「神ツール」とは言い難いので、もっと強力な道具が欲しいところです。

チョムスキー階層

さきほど「有限オートマトンと正規言語には切っても切れない関係がある」と言いましたが、実はこの「切っても切れない関係」、すなわち「装置と言語のペア」というのは他にもいくつかあるのです。代表的なものがチョムスキー階層と呼ばれる 4 組のペアです。

装置	言語
有限オートマトン	正規言語
プッシュダウンオートマトン	文脈自由言語
線形拘束オートマトン	文脈依存言語
チューリングマシン	帰納的可算言語

この四つのペアなのですが、下にあるものほどつよいです。具体例を挙げると「文脈自由言語」は正規言語を全て含みます。よって「プッシュダウンオートマトン」は有限オートマトンに解ける問題は全て解けますし、それに加えて有限オートマトンに解けない問題のいくつかも解くことができます。

ここでタネ明かしをすると「回文言語」は「文脈自由言語」です。なのでプッシュダウンオートマトンは有限オートマトンと違って回文判定問題が解けますし、「4 の倍数判定問題」も当然のように解けます。

さて下にあるものほどつよいなら、最強はチューリングマシンということになります。名前を耳にしたことがある人も少なくないのではと思います。この記事の本題である P ≠ NP 問題の解説にはチューリングマシンは絶対に欠かせないので、ここから長い長い説明が始まります。

「神ツール」バージョン 4：チューリングマシン

そういうわけで「神ツール」バージョン 4 のチューリングマシンです。バージョン 2 に当たるプッシュダウンオートマトンとバージョン 3 に当たる線形拘束オートマトンは今回は省きます。

さて、チューリングマシンの本格的な説明に入る前に、ちょっと有限オートマトンを別の切り口からとらえてみます。

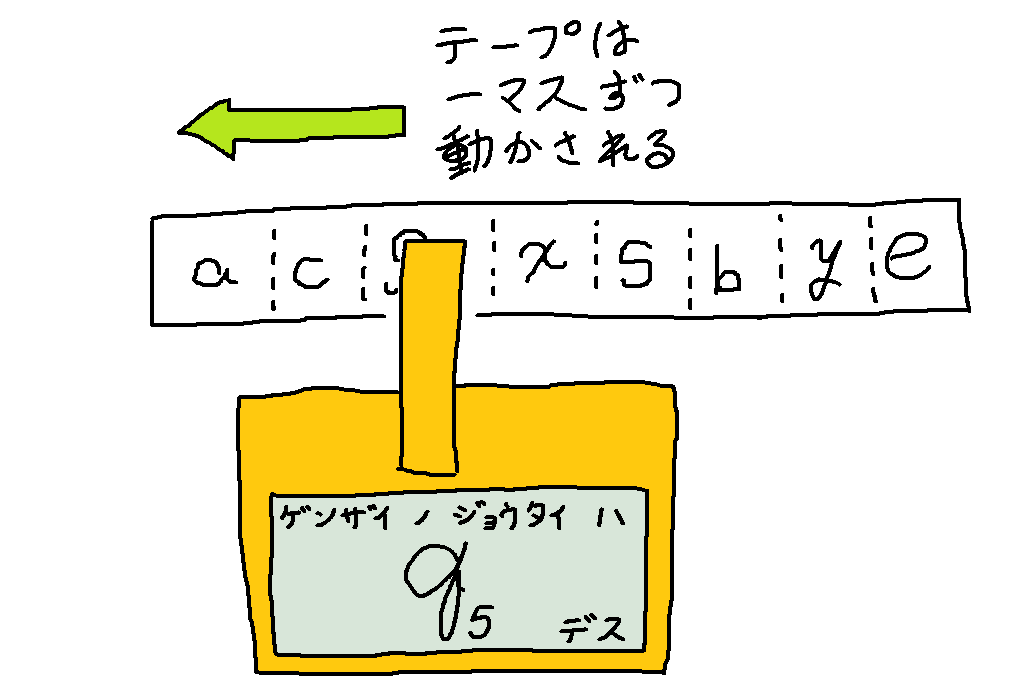
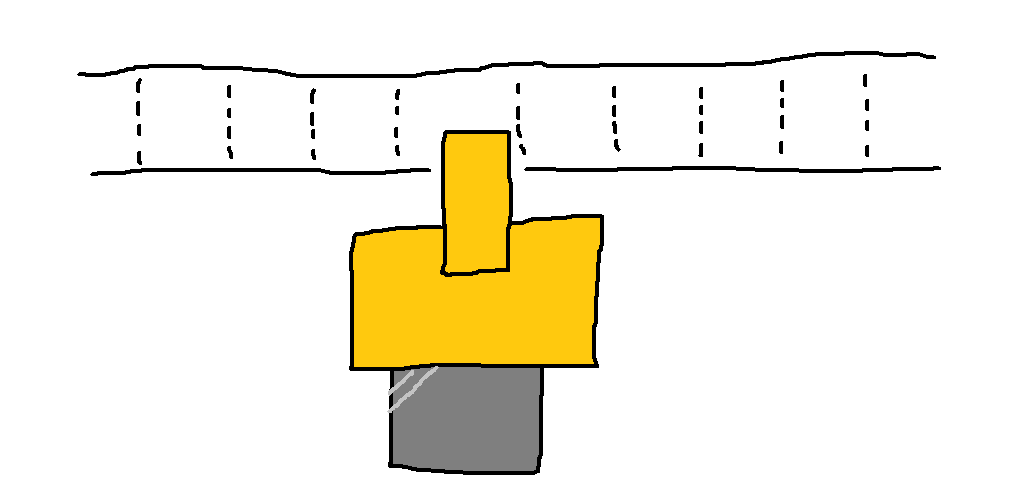
有限オートマトンは入力された文字列を先頭から順に読み込んでいきながら「丸」を動いていき、最終的に「二重丸」に到達したらオッケーという仕組みでした。ちなみにこの「丸」を状態、「二重丸」を受理状態といい、受理状態ではない状態を拒否状態といいます。さて有限オートマトン自体はあくまでも思考の世界にのみ存在するものなのですが、これを実際に電子工作するならばこんな設計になるでしょう。

このハードウェアは「テープ」に書かれた文字列を「ヘッダ」を用いて読み取ります。そして読み取った文字に応じて内部に記録されている状態を更新していきます。シンプルな機械ですね。

ところでこのハードウェアにおいてテープは読み取り専用です。事前にテープに書き込まれた内容が機械によって書き換えられることはありません。さらにもう一つ自明な事実として、テープは必ず一方向にのみ動きます。図で示したハードウェアの場合テープは左向きにのみ動きます。

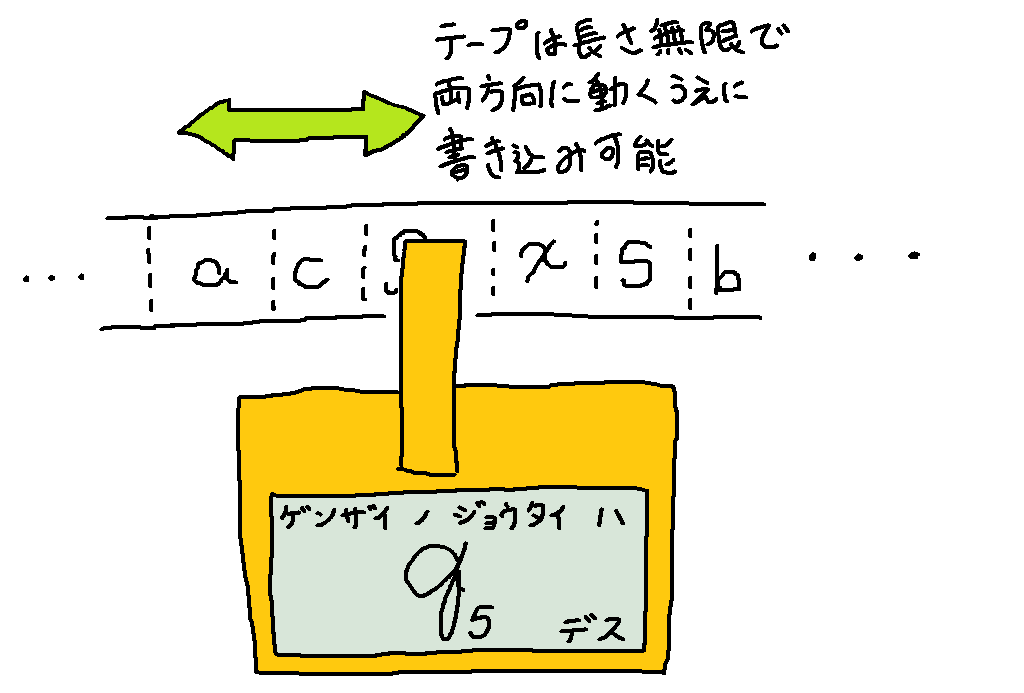
さて、実はこのテープの長さを無限にして、さらに書き込み可能にして、さらに左右両方向に動かせるようにしたものがチューリングマシンに当たります。

もう少し正確な説明に入ります。まずは「テープ」に入力を書き込みます。ただし有限オートマトンの時とは違ってテープは両方向に無限の長さを持つので、端というものがありません。なので適当な場所に入力を書き込み、その 1 文字目がチューリングマシンのヘッダの真下に来るようにテープをセットし、チューリングマシンの電源を入れます。また、「何も書かれていないマス」には便宜的に「空白記号」が書き込まれているものとします。

有限オートマトンは「現在の状態」と「読み取った文字」から「次の状態」を決めていました。チューリングマシンでも似たようなことをします。ただしチューリングマシンは「現在の状態」と「読み取った文字」から「ヘッダの真下にある文字をどの文字へと書き換えるか」「次の状態」「テープを左右どちらに 1 マス動かすか」の三つを決めます。

ということで、チューリングマシンの動作はこんな感じになります。

1. ヘッダから文字を読み取る
2. 決められた規則に従ってヘッダの真下にある文字を書き換える
3. 決められた規則に従って状態を更新する
4. 決められた規則に従ってテープを左右どちらかに 1 マス動かす
5. 以下繰り返し

ただしこの「決められた規則に従って」というところですが、実は「次の状態」「どの文字に書き換えるか」「テープをどっちに動かすか」が決められていないということがありえます。この場合チューリングマシンは停止します。停止した時点での状態が受理状態であったならばチューリングマシンの回答は Yes、そうでなかったなら回答は No です。

チューリングマシンのちゃんとした定義

チューリングマシン $T$ は七つ組 $\langle \Gamma, b, \Sigma, Q, q_{\mathrm{init}}, F, \delta \rangle$ です。それぞれ以下のように定められます。

• $\Gamma$（字母）：空でない有限集合。またこの元を記号という。
• $b$（空白記号）：$\Gamma$ のとある元。
• $\Sigma$（入力字母）：$\Gamma \setminus \{b\}$ の部分集合（空でもよい）。またこの元を入力記号という。
• $Q$（状態集合）：空でない有限集合。またこの元を状態という。
• $q_{\mathrm{init}}$（初期状態）：$Q$ のとある元。
• $F$（受理状態集合）：$Q$ のとある部分集合。空でもよい。またこの元を受理状態という。
• $\delta$（遷移関数）：$\Gamma \times Q$ から $\Gamma \times Q \times \{L, R\}$ への部分写像。

まず $T$ への入力文字列 $\sigma_1\sigma_2\cdots\sigma_n$（各 $\sigma$ は $\Sigma$ の元）を、空白記号のみが両方向に無限個記入されたテープの適当な位置に書き込みます。ここで $\sigma_1$ が書き込まれた位置を $T$ がテープの読み取りを開始する地点とします。

入力を与えられた $T$ は初期状態を $q_{\mathrm{init}}$ とした後、以下を繰り返します。

1. ヘッダから読み取れる文字を $c$、現在の状態を $q$ とし、$\delta(c, q)$ が定義されているならばそれを $(c', q', D)$ と置く。定義されていなければ繰り返しから抜ける。
2. ヘッダの真下にある文字を $c'$ に書き換える。
3. 状態を $q'$ に更新する。
4. $D = L$ ならばテープを左に 1 マス動かし、$D = R$ ならテープを右に 1 マス動かす。

$T$ が停止した時点での状態が $F$ の元であるならば $T$ は入力を受理したといい、そうでなかった場合 $T$ は入力を拒否したといいます。また $T$ が永遠に停止しない場合 $T$ は入力に対し停止しないといいます。

さて先ほどはチューリングマシンが最強という話をしました。しかし本当にこんなもんでまともな計算ができるのか疑わしいので、有限オートマトンで倍数判定ができることを示したようにチューリングマシンでも何かしらのデモがしたいところです。ただ残念ながらチューリングマシンでそれなりの計算をするとなるとそれなりに複雑な設計が必要となってしまうので、チューリングマシンの可能性を簡易的かつ端的に示すようなデモはちょっと難しいです。

そこで代わりといっては何ですが、皆さまに衝撃の事実をお伝えしたいと思います。皆さまは今パソコンやスマホでこの記事を読んでいらっしゃることと思いますが、チューリングマシンは皆さまがお使いのパソコンやスマホと同等の計算能力を持ちます。もう少し正確に言えば、パソコンやスマホで解ける問題はすべてチューリングマシンで解けます。スーパーコンピューターを使って計算するような物理シミュレーションやら天気予報やらも、やろうと思えばチューリングマシンで計算できてしまうのです。

もちろんこれらの問題は「はい・いいえ」で答えられる問題ではないので決定問題ではなく関数問題ですが、関数問題をチューリングマシンに解かせることも可能です。チューリングマシンはテープへの書き込みができるので、停止した時点でのテープの内容を「回答」とみなせば関数問題にも回答できるのです。

余談その 1：万能チューリングマシン

この節で説明する万能チューリングマシンは P ≠ NP 問題の説明には要らないものではあるのですが、とても面白い話なのでついでにお話しておきます。

先ほど「チューリングマシンはコンピュータと同じくらいの性能を持つ」というお話をしました。なので「倍数判定をするチューリングマシン」とか「回文判定をするチューリングマシン」とか「素数判定をするチューリングマシン」などというものも当然作れます。

ただし有限オートマトンと同じくチューリングマシン自体は思考の世界にのみ存在するものです。なのでチューリングマシンに実際に仕事をしてもらうのであれば秋葉原あたりで電子部品を買ってきて実際にチューリングマシンを組み立てる必要があります。

ですが、解きたい問題ができるたびに秋葉原に行って、新しいチューリングマシンを組み立てなおすなんて面倒極まりないですよね？そこで、どうにかしてたった 1 台のチューリングマシンであらゆる計算をすませたいところです。

・・・さて、有限オートマトンの導入の時に「入力のフォーマットを文字列に統一する」という話をしたのを覚えているでしょうか。数やグラフなどの様々な概念を有限オートマトンで処理するため、そういった形のない概念は文字列に書き起こして入力しようという話でした。

実際「文字列」というものの表現能力は非常に高いのです。そこで、チューリングマシン自体を文字列として書き起こしてしまいます。

「は！？そんなことどうやってやるの！？」と思うかもしれませんが、難しく考える必要はありません。先ほども言ったようにチューリングマシンはお手元のパソコンと同等の計算能力を持つので、チューリングマシンを表す全情報（そのチューリングマシンが使う文字の集合、遷移規則の内容など）がなんらかのフォーマットで記されていればそれでオッケーです。それこそ JSON や XML などでもかまいません。とにかく、チューリングマシンを具体的にどうやって文字列にするのかはあまり重要ではないのです。

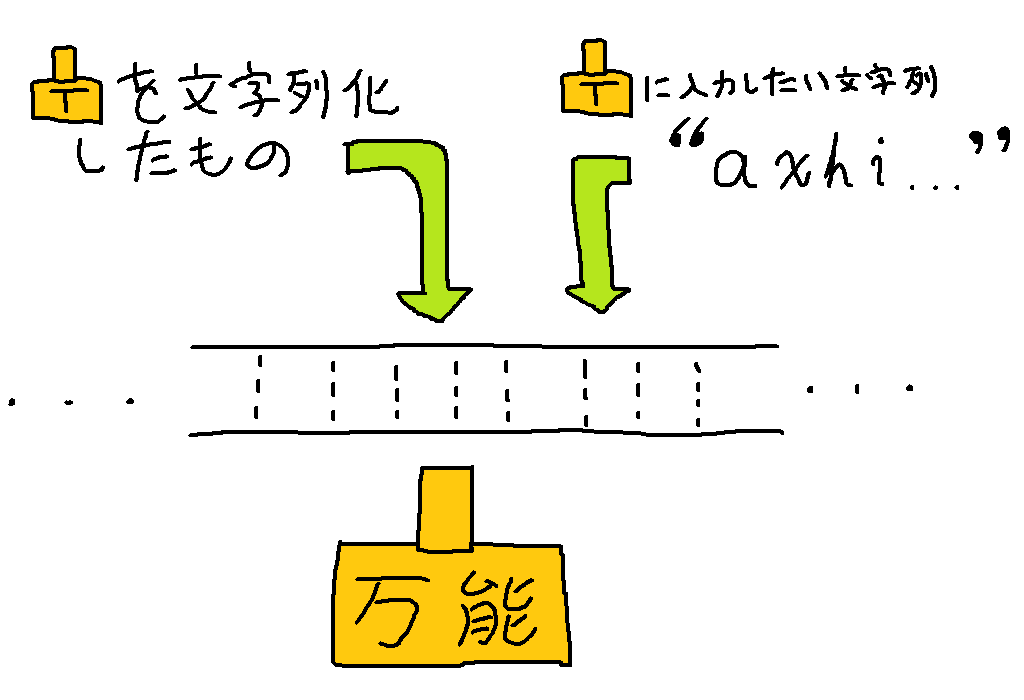
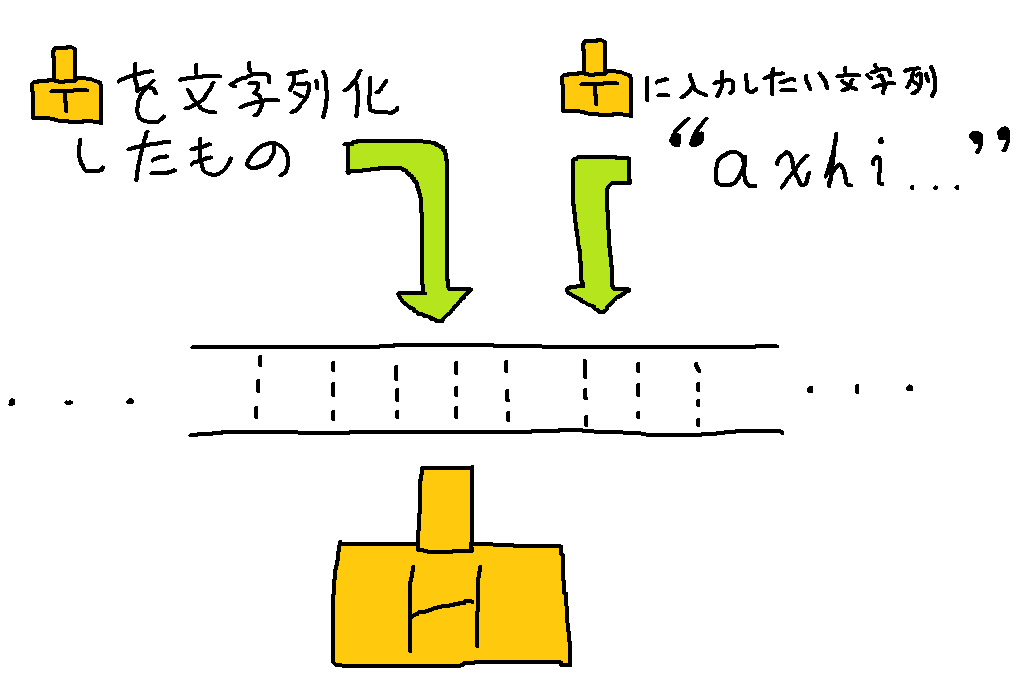
さて、ついに万能チューリングマシンのご紹介です。万能チューリングマシンは「チューリングマシン $T$¹ を文字列として書き起こしたもの」と「$T$ に入力したい文字列」の二つを入力として受け取ります。

入力の文字列が二つもありますが、この二つの文字列は「適当な方法」で連結して一つの文字列にしてしまえばよいです。「チューリングマシンを文字列にする方法」と同じく、ここでも具体的な方法は重要ではありません。とにかく何らかの方法でやってしまえばいいのです。この記事の続きでも 1 台のチューリングマシンに複数の文字列を入力する場面がありますが、そこでも実際には「適当な方法」で作った一つの文字列を入力していると考えてください。

このように「文字列化したチューリングマシン $T$」と「$T$ への入力」を受け取り、$T$ に入力を与えたときの計算結果を模倣するチューリングマシンを万能チューリングマシンといいます。すなわち仮に $T$ が入力に対して受理状態で停止するようなチューリングマシンであったならば万能チューリングマシンも受理状態で停止し、逆に $T$ が入力に対して拒否状態で停止するようなチューリングマシンであったならば万能チューリングマシンも拒否状態で停止します。また $T$ の最終的な出力も適当に模倣します。

出力を模倣するとはどういうことかという話ですが、例えば $T$ の使用する文字は "a", "b", "c" の 3 文字で、一方の万能チューリングマシンの使う文字は "0", "1" の 2 文字だった場合を考えます。ここで $T$ の最終的な出力が "abc" だったとしても、万能チューリングマシンの使える文字は "0" と "1" の 2 文字しかないわけですから、"abc" という文字列そのものを万能チューリングマシンが印字することはできませんよね？なので、万能チューリングマシンは自分に印字できる文字のみを使用し、$T$ の出力を模倣するのです。例えば "abc" それぞれの ASCII コードを並べて "011000010110001001100011" とかにするわけです。

さて万能チューリングマシンが 1 台あればもう自宅と秋葉原を往復する必要はなくなります。何か新しい計算がしたくなったときにはその計算を行うチューリングマシンの設計図だけを作り、それを万能チューリングマシンに入力すればよいのです。

ところでこの「チューリングマシンの設計図を作る」、そして「それを万能チューリングマシンに入力する」というところ、何かピンとくる方はいないでしょうか。これって、プログラミングそのものですよね。そう、つまり皆さまがお使いのパソコンは万能チューリングマシンだったのだ！！！

ただし定義上のチューリングマシンは「無限の長さのテープ」、すなわちコンピュータで例えるなら「無限のメモリ」を持っているので、現実世界に存在するコンピュータは厳密な意味ではチューリングマシンではありません。ただし 1 台のパソコンに含まれるメモリをすべて同時に使うことなどそうはありませんし、実用上はチューリングマシンとみなして問題ありません。

チューリングマシンの定義そのものは非常に簡単なものでした。なのでそれを C 言語などのプログラミング言語で実装するのも至極簡単なことです。つまり、こういったプログラミング言語はチューリングマシンと同等の表現能力を持つと言えます。このことをチューリング完全性といいます。

C 言語を始めとするほぼすべて²のプログラミング言語はチューリング完全です。なので、どんなプログラミング言語でどんなプログラムを作ることも（理論上は）可能ということになります。「C 言語では作れるけど Python では作れないプログラム」なんてありませんよね。ほかにも変わり種としてはライフゲーム³とかマリオメーカー⁴とかマジック：ザ・ギャザリング⁵とかがチューリング完全です。

余談その 2：チューリングマシンの限界

いや～素晴らしいですね、チューリングマシン。もはやできないことなんてなさそうです。

・・・と言いたいところですが、残念ながらチューリングマシンにさえ解けない問題もあります。その代表例が停止性問題です。「停止性」とは一体なんでしょうか？

ここで有限オートマトンのことを思い出しましょう。有限オートマトンは入力から 1 文字読み取るたびに状態を遷移していくというシステムでした。つまり有限オートマトンは入力の長さに比例した計算時間がかかるわけですが、それでも入力の長さが有限である以上いつかは必ず計算が終わります。

ところが困ったことにチューリングマシンはそうではありません。下手な設計をしてしまったチューリングマシンは特定の入力に対し永遠に停止しなくなってしまう場合があるのです。

先ほど「ほとんどのプログラミング言語はチューリング完全である」、すなわちチューリングマシンを表現できるという話をしましたが、例として Python で「特定の入力に対して停止しないチューリングマシン」を表現するとこんな感じになります。

x = input()

if x == 'foo':
    while True:
        pass

このプログラムは foo と入力されたとき永遠に停止しなくなります。この程度の簡単なプログラムであればそれは一目瞭然ですが、もうちょっと大規模なプログラムになると判別は難しくなりそうです。

チューリングマシンが停止しないことの何がまずいのかというと、チューリングマシンを動かしている私たちの立場からすれば、そのチューリングマシンがただ計算に時間がかかっているだけなのか、それとももう永遠に止まらなくなってしまっているのか見分けがつかないということです。つまり、辛抱強く待ち続ければいつかは計算は終わるのか、それとももういくら待っても無駄なのか、それがわからないままいつまでも待たされることになってしまうのです。

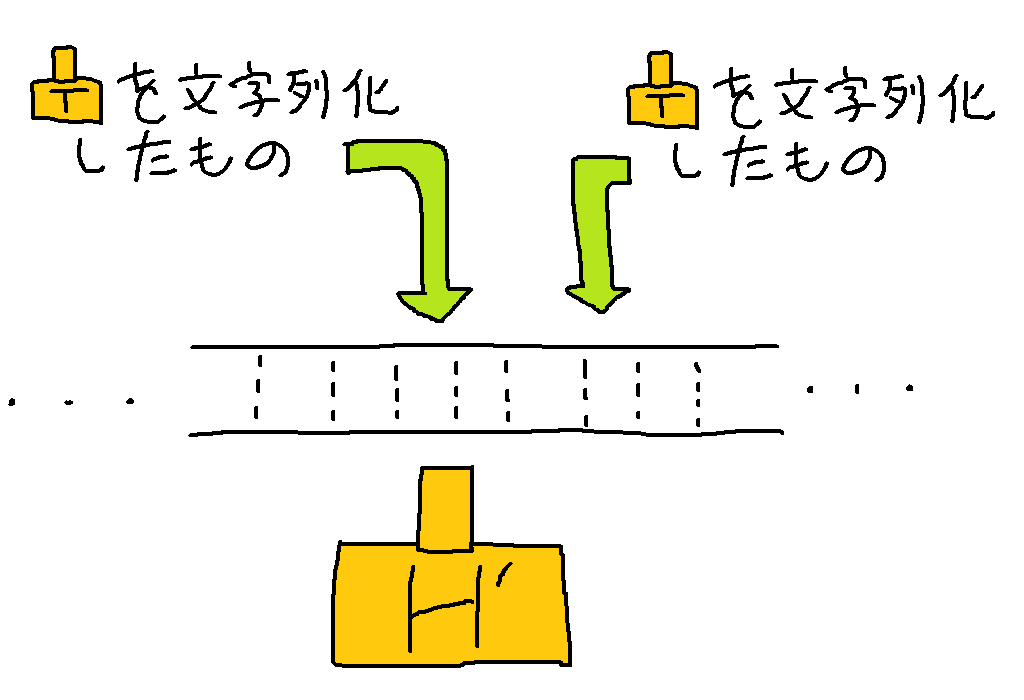
なので「チューリングマシンが停止するのかしないのか」を事前に知ることが出来たらものすごく便利ではないでしょうか。「いつかは停止するよ！」という判定結果であれば安心して待ち続けることができますし、「停止しないよ！」という判定結果であれば無駄な時間を浪費せずに済みます。このように、「チューリングマシンが停止するのかしないのか」を判定する問題を停止性問題といいます。停止性問題を解くチューリングマシン $H$ ⁶はこんな感じになるでしょう。入力されるものは万能チューリングマシンと一緒です。

「チューリングマシン $T$ を書き起こした文字列」と「$T$ への入力」を受け取り、$T$ が入力に対して停止するのであれば $H$ は受理状態で停止します。また $T$ が停止しない場合は $H$ は拒否状態で停止します。こんなものがあったら便利ですね。

さて、もし $H$ が作れるのならばこんなチューリングマシン $H'$ も作れてしまうはずです。

$H'$ は「チューリングマシン $T$ を書き起こした文字列」を受け取ります。そして $T$ が $T$ 自身を書き起こした文字列に対して停止するならば $H'$ は自発的に無限ループに突入し、逆に $T$ が自分自身に対して停止しないならば $H'$ は停止します。

ここで問題です。$H'$ に $H'$ 自身を入力したらどうなるでしょうか？

仮に $H'$ が $H'$ 自身を入力されたときに停止したとします。$H'$ は「チューリングマシン $T$ が $T$ 自身に対して停止しないとき」にのみ停止します。つまり $H'$ が $H'$ に対して停止したならば、$H'$ は $H'$ に対して停止しないということになります。これは明らかな矛盾です。

逆に、$H'$ が $H'$ 自身を入力されたときに停止しなかったとします。$H'$ は「チューリングマシン $T$ が $T$ 自身に対して停止するとき」にのみ停止しません。つまり $H'$ が $H'$ に対して停止しなかったならば、$H'$ は $H'$ に対して停止するということになります。これも明らかな矛盾です。

したがって、$H'$ は $H'$ を入力されたときに停止するとしても停止しないとしても矛盾してしまいます。よってチューリングマシン $H'$ は存在せず、$H'$ が存在しないことから $H$ も存在しません。したがって、停止性問題は解けません。つまり停止するのかしないのかわからないプログラムを動かしているときにはもう祈るしかないということです。† アーメン †

第 2 部：P 問題と NP 問題

さてつい熱くなって横道にそれすぎてしまいましたが、そろそろ本題に戻ってきます。ここから先は計算理論の下位分野であり、ある問題を解くのはどのくらい大変なのかを論じる計算複雑性理論に突入します。

計算複雑性理論でもチューリングマシンを活用していきます。またここでは問題の「大変さ」を以下のように 2 種類定めます。

• 時間計算量：ある問題をチューリングマシンで解くときにどれくらい時間がかかるか。より厳密には停止するまでに何回の状態遷移を行う必要があるか。
• 空間計算量：ある問題をチューリングマシンで解くときにどれくらい記憶領域を必要とするか。より厳密にはテープ上のマスをいくつ読み書きする必要があるか。

実のところ空間計算量が問題にされることはあまりありません。我々が挑もうとしている P ≠ NP 問題も時間計算量に関わる問題なので、この時間計算量について考えていきましょう。

時間計算量

まずはこちらの問題をご覧ください。

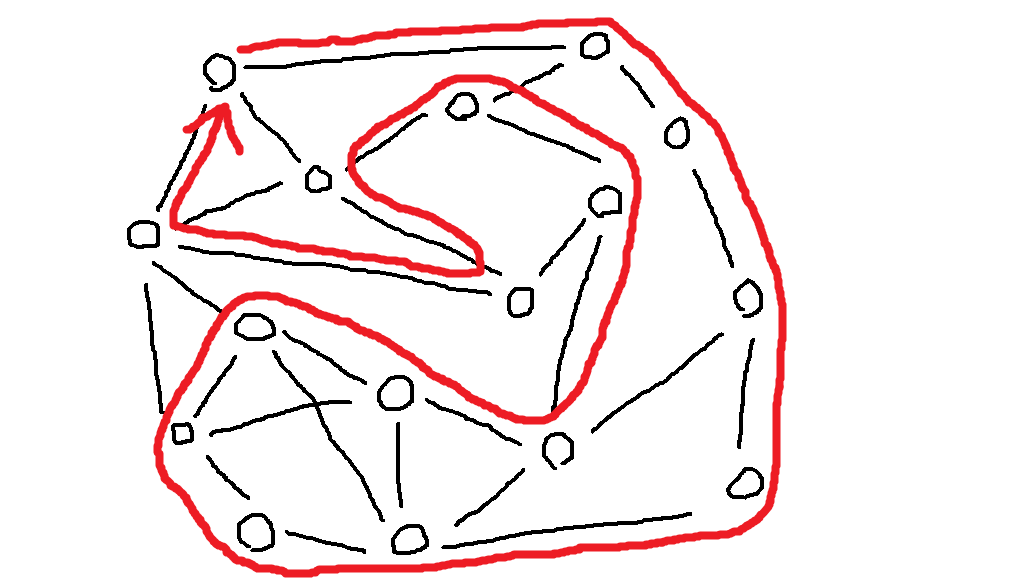
グラフが与えられるので、一筆書きでスタート地点まで戻ってこられるか判定せよ。
（ただし話を簡単にするために入力されるのは単純連結無向グラフであるとします。以下同様）

この問題はオイラー閉路問題と呼ばれます。グラフ上でスタート地点まで戻ってくる一筆書きを専門用語で「オイラー閉路」といい、それの存在を判定するのでオイラー閉路問題というわけです。

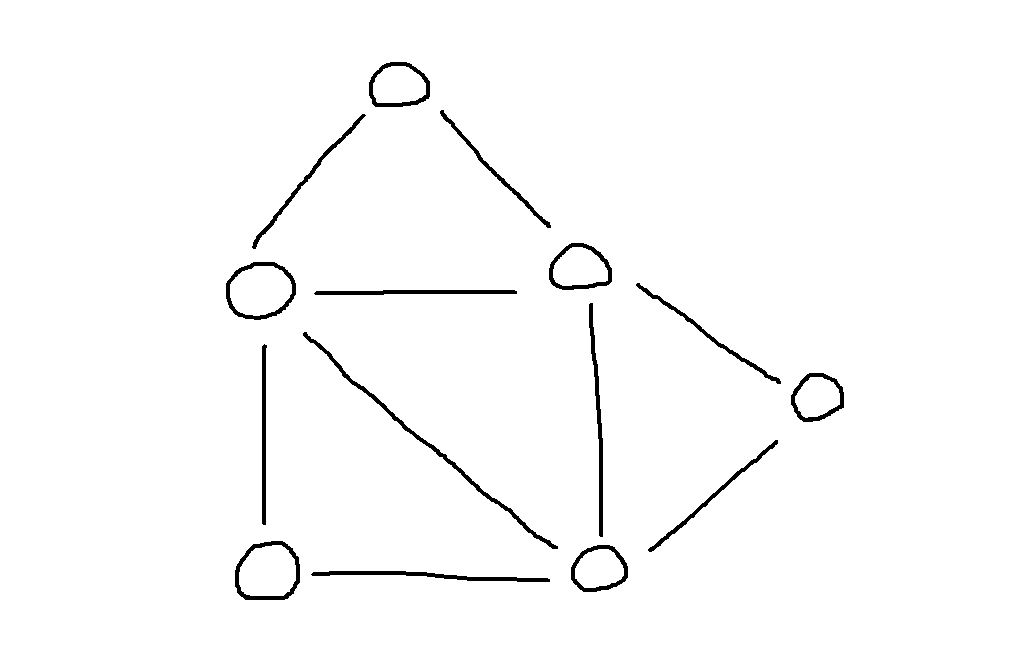
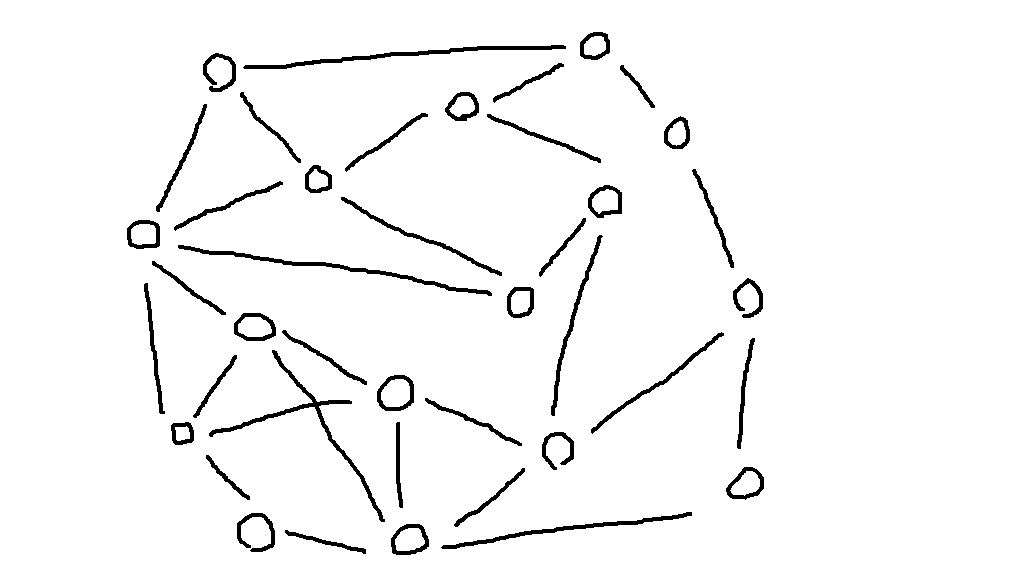
例えばこんなグラフが与えられたとします。

証明は省略しますが、オイラー閉路は「すべての頂点が偶数本の辺と繋がっている」ときにのみ必ず存在するという定理があります。上に示したグラフはこの条件を満たすのでオイラー閉路を持ちます。

この問題をチューリングマシンで解くことを考えます。チューリングマシンには「適当な方法」で文字列化したグラフを入力し、そのグラフにオイラー閉路が存在するか判定してもらいます。上に書いた定理より判定にはすべての頂点を 1 個ずつ見ていき、その頂点が偶数本の辺と繋がっていることを確認すればよいです。なので、このチューリングマシンは概ね入力の長さに比例する計算時間で停止するといえます。

ここがちょっと雑な議論になってしまっています。具体的な計算時間は「文字列でどうグラフを表現するか」と「チューリングマシンをどう実装するか」によって変わってきますが、例えば調べたいグラフが隣接行列としてテープに書き込まれているとします（隣接行列は「数字」と「適当な区切り文字」で表現できるのでテープに書き込めますよね）。するとこの隣接行列によって表現されたグラフがオイラー閉路を持つかどうかは「全ての行（または列）が偶数個の 1 を含む」ことだけ判定すればいいので、基本的にはテープに書かれた文字を先頭から順に読んでいけば処理できそうです（ときおり引き返すことはあるでしょうが）。なので計算時間は概ね入力の長さに比例するといえます。少なくとも入力の長さの 2 乗や 3 乗に比例するようなことにはならないでしょう。

まあ、細かい話は抜きにしてこういうことになります。

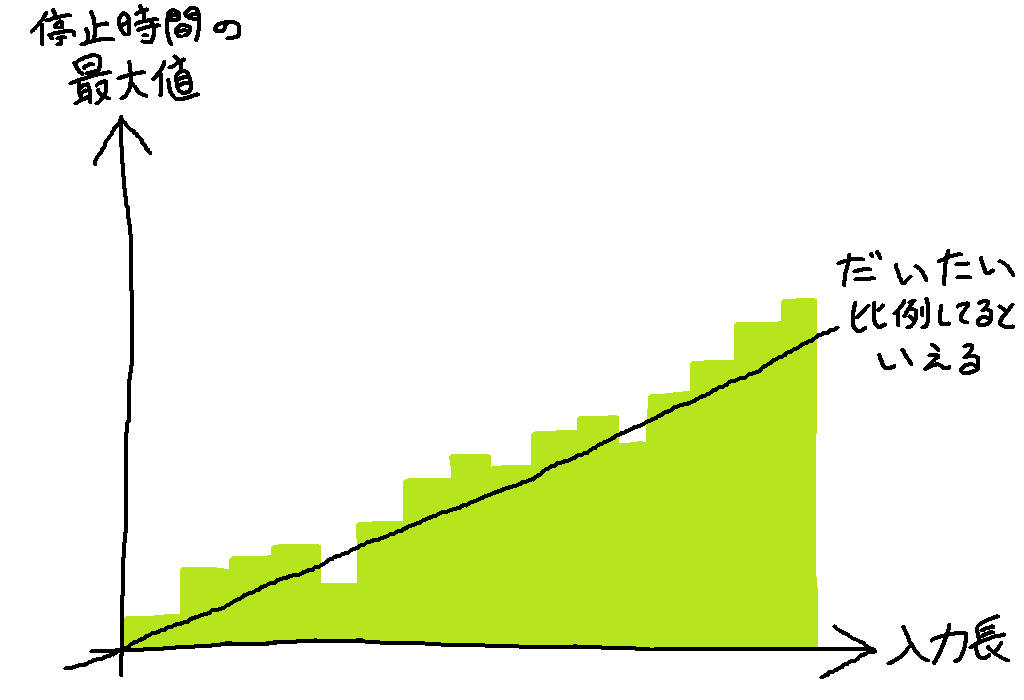
横軸は「入力の長さ」、縦軸は「停止するまでに必要な時間の最大値」です。ちょっと混乱してきましたか？

例えば「長さが 3 の文字列」は "abc" とか "baa" とかいっぱいありますよね。有限オートマトンであれば文字列の内容は関係なく文字列の長さだけで計算時間が決まったわけですが、チューリングマシンは有限オートマトンとは違って入力の長さが同じであったとしても停止するまでにかかる時間は異なる場合があります。そこで、「長さが 3 の文字列」を入力されたときの最大値を縦軸にとるというわけです。

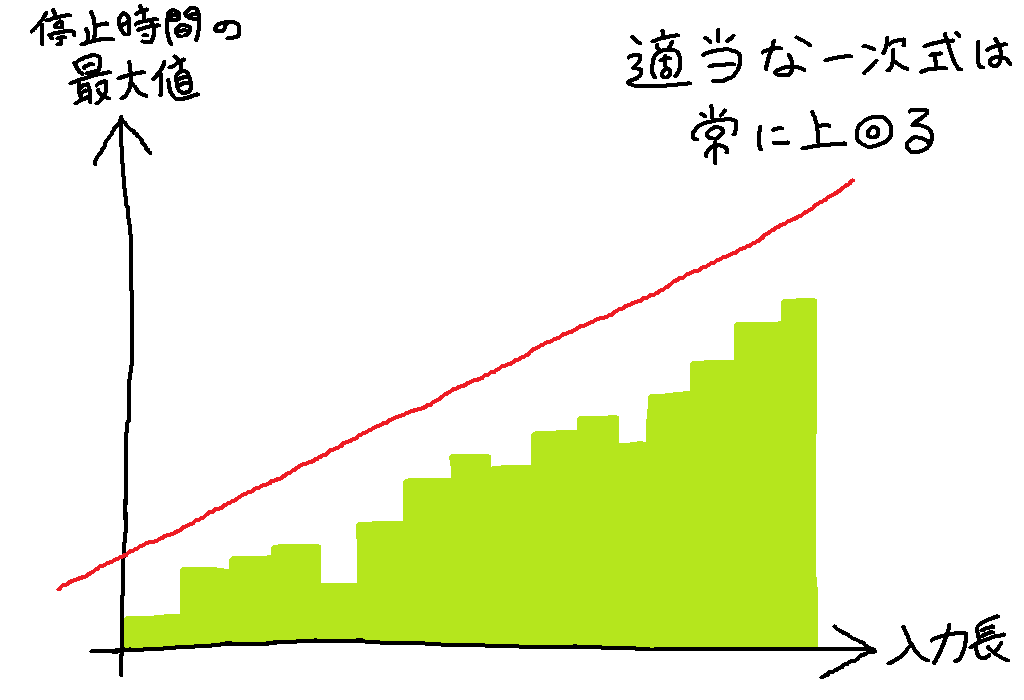
さて、上のグラフは厳密に比例の形になっている訳ではありません。多少上下にガタガタしている部分もあります。しかしそれでも概ね比例の形になっているとはいえるので、このチューリングマシンの計算時間は適当な 1 次式で押さえつけられるといえます。つまりこういうことです。

適当に大きな傾き $a$ と適当に大きな切片 $b$ を持ってくれば、1 次式 $ax + b$ は「チューリングマシンが長さ $x$ の文字列に対して停止するのにかかる最大時間」を常に上回るようになります。よって、このチューリングマシンの計算時間は 1 次式で押さえつけられるといえます。

それでは次にこの問題をご覧ください。

グラフが与えられるので、全ての頂点をちょうど 1 回だけ通ってスタート地点まで戻ってくる経路が存在するか判定せよ。

こっちの問題はハミルトン閉路問題と呼ばれます。オイラー閉路は「全ての辺をちょうど 1 回通ってスタート地点まで戻ってくる経路」だったのに対し、ハミルトン閉路は「全ての頂点をちょうど 1 回通ってスタート地点まで戻ってくる経路」です。オイラー閉路問題は「すべての頂点が偶数本の辺と繋がっているか確認する」という効率の良い解き方があったわけですが、残念ながらハミルトン閉路問題には効率のいい解き方が見つかっていません。なので、基本的には総当たりするしかありません。

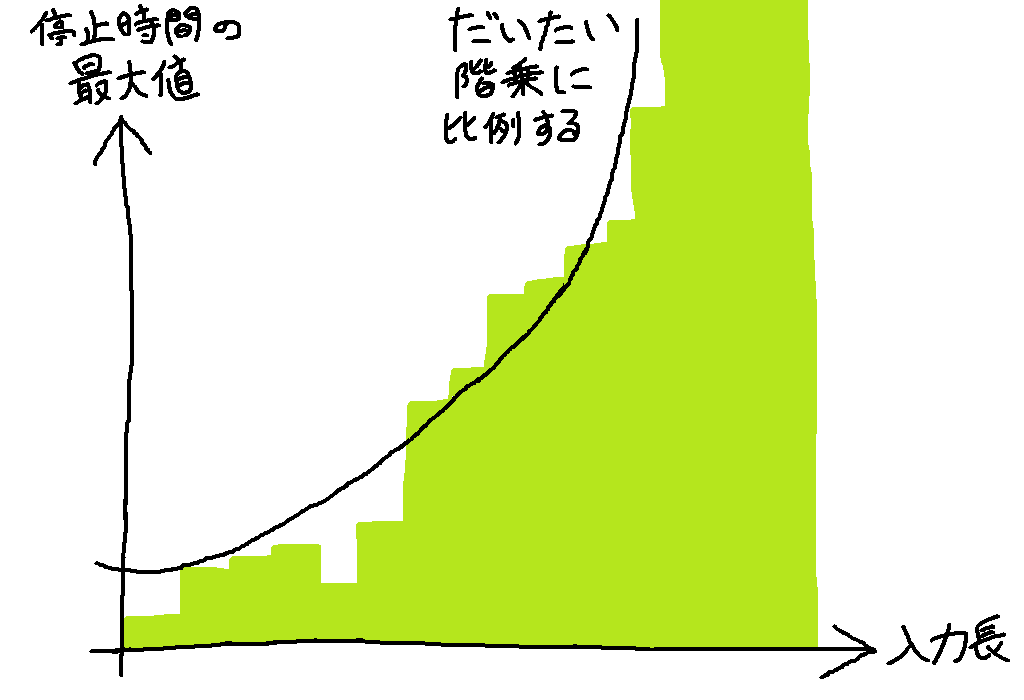
例えば「すべての頂点の順列を総当たりする」という方針で答えを求める場合、頂点数 $V$ に対し概ね $V!$ に比例する計算時間がかかってしまいます。よってチューリングマシンが停止するまでにかかる時間のグラフはこんな感じになります。

このグラフは「概ね」とはいえ階乗のペースで増加していくので、1 次式で押さえつけるのはどう考えても不可能です。どんなに大きな傾きとどんなに大きな切片を持ってきてもいずれ追い抜かれてしまいます。

1 次式でなく 2 次式であったとしても 3 次式であったとしても、極端な話 1 兆次式であったとしてもいつかどこかで追い抜かれてしまいます。階乗とはそれほど恐ろしいものなのです。

P 問題

オイラー閉路問題とハミルトン閉路問題は見かけこそ似ているものの計算に必要な時間は月とスッポンでした。さて、実は今我々が学んでいる計算複雑性理論の世界にはある一つの「経験則」があります。それは、計算時間が入力長の多項式で押さえつけられる問題は「わりとすぐ解ける問題」で、そうでない問題は「すぐには解けない問題」だということです。

計算理論で扱う問題のうち「わりとすぐに解ける」、言い方を変えれば「現実的に解ける」問題を tractable problem といいます。例えば、頂点が 1 兆個あるグラフに対してハミルトン閉路問題を解くことは理論上は可能ですよね？ただ 1 兆の階乗通りの経路を総当たりすればいいだけですから。しかし、いくら「理論上は可能」とはいっても現実的にはどう考えても不可能です。つまりただ単に「理論上は可能である」にとどまらず、現実的な計算資源で解ける問題を tractable というのです。例えばハミルトン閉路問題でも、頂点がせいぜい 10 個くらいであれば十分 tractable です。

そして「計算時間が入力長の多項式で押さえつけられる問題は tractable である」という主張を Cobham–Edmonds の提唱といいます。ただし、これはあくまでも「提唱」であって「定理」ではないことには注意してください。

以下、「入力長の多項式で押さえつけられる計算時間」を多項式時間と呼ぶことにします。もちろん入力長の 1 兆乗に比例する時間なんかも一応 1 兆次式という多項式で押さえつけることはできるので多項式時間ではあるのですが・・・

ハミルトン閉路問題の計算時間はざっくりと入力長の階乗に比例していたので、どんな多項式でも押さえつけることはできませんでした。なのでこの問題は「すぐには解けない問題」（より正確には「すぐに解く方法が見つかっていない問題」）ということになります。一方オイラー閉路問題の計算時間は「入力長の 1 次式」で押さえつけることが可能でした。1 次式はもちろん多項式ですから、この問題は「わりとすぐ解ける問題」といえます。このように、チューリングマシンを用いて入力長の多項式時間で解ける決定問題を P 問題といいます。"P" は Polynomial（多項式）の略です。

より厳密には、「入力文字列が所与の言語に属しているか否か」という決定問題を入力文字列の長さの多項式時間で回答できるときにその決定問題を P 問題といいます。オイラー閉路問題における「所与の言語」とはオイラー閉路を含むグラフを表現した文字列の集合です。つまり、オイラー閉路問題を解くチューリングマシンは正確にはこのような動作をする必要があります。

• 入力文字列がそもそもグラフを表現していない文字列である場合、No と回答する。
• グラフを表現している文字列だったとしても、そのグラフにオイラー閉路が存在しない場合はやはり No と回答する。
• グラフを表現している文字列で、なおかつそのグラフにオイラー閉路が存在している場合は Yes と回答する。

さっきまではオイラー閉路問題を解くチューリングマシンには必ず「グラフを表現した文字列」が入力されるという暗黙の了解を置いてしまっていましたが、実際には「入力文字列が本当にグラフを表現しているのか？」という判定も含めて多項式時間で終わらせる必要があります。

さて、P ≠ NP 問題とは P 問題と NP 問題の違いを論じるものです。それでは NP 問題とはなんでしょうか？

「非決定性」

ハミルトン閉路問題は $V!$ 個の経路をすべて総当たりしなければ答えが見つからないわけでしたが、実はもっと効率的に答えを求める方法があります。なんだかわかりますか？

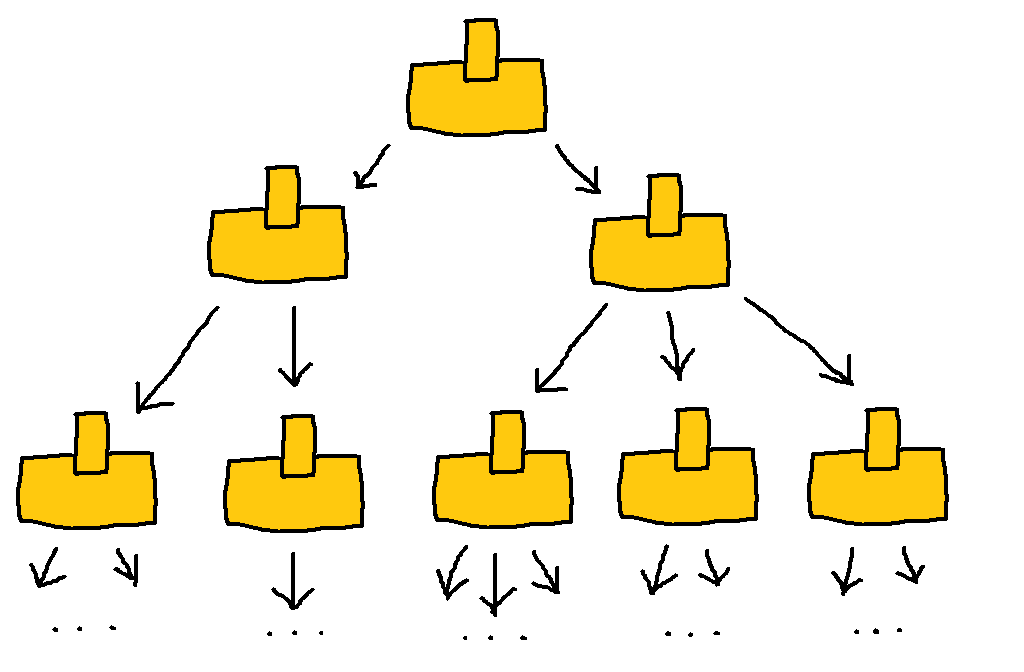
・・・答えは、「全ての経路を一斉に調べる」です。$V!$ 個の経路を 1 個ずつ順番に調べるのではなく、全部同時に調べるのです。それを可能にしてしまうのが非決定性チューリングマシンです。

先ほどチューリングマシンの定義についてお話ししましたが、あれは正確には決定性チューリングマシンと呼ばれるものの定義です。決定性チューリングマシンは「ヘッダから読み取れる文字」と「現在の状態」から「次にすべきこと」がただ一つ明確に決まりました。それゆえの「決定性」です。それに対し、非決定性チューリングマシンは「次にすべきこと」がただ一つに決まるとは限りません。つまり、非決定性チューリングマシンは次のステップで状態 $q_i$ に遷移するかもしれなければ、状態 $q_j$ に遷移するかもしれないのです。あるいは $q_i$ でも $q_j$ でもない他の状態に遷移するかもしれません。

「そんな、どんな動作をするかもわからない機械で計算なんてできるわけないじゃないか！」と思われるかもしれませんが、じつはこの非決定性チューリングマシンはとんでもない計算能力を持っています。非決定性チューリングマシンは、状態遷移のたびに世界線が分岐するのです。

・・・は！？

非決定性チューリングマシンの解釈

ちょっと誇張しすぎました。いま言ったのは、あくまでも「『世界線が分岐している』と解釈すれば動作がわかりやすい」程度の話です。それでは具体的に見ていきましょう。

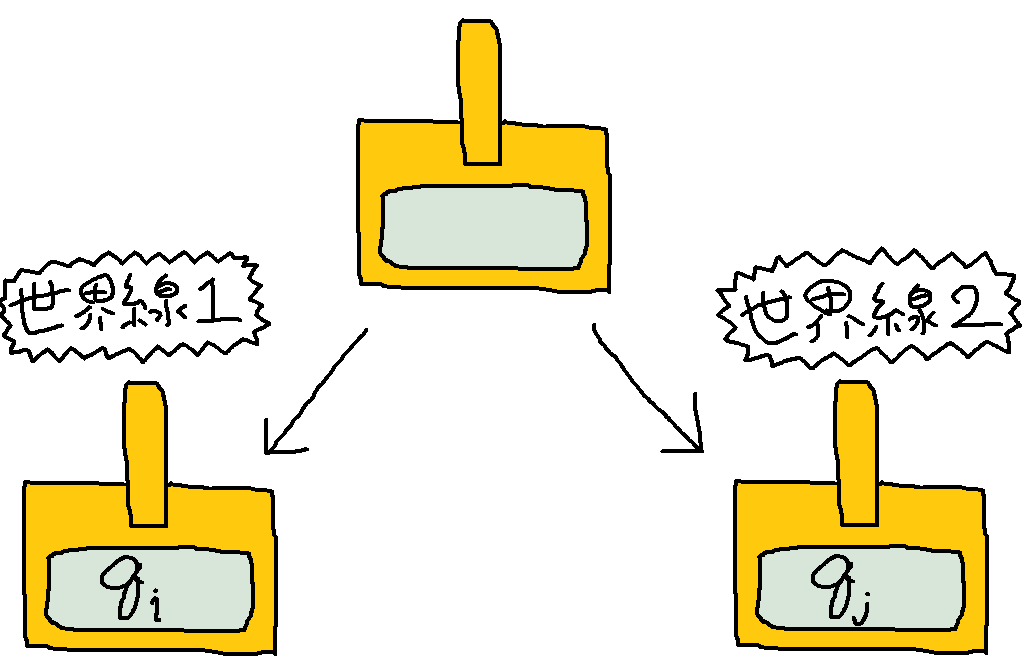
ここに 1 台の非決定性チューリングマシンがあるとします。先ほどもお話ししたようにこの非決定性チューリングマシンは次のステップで状態 $q_i$ に遷移するかもしれませんし、あるいは状態 $q_j$ に遷移するかもしれません。これは、非決定性チューリングマシンが状態 $q_i$ に遷移した世界線と状態 $q_j$ に遷移した世界線に分岐すると考えればよいのです。

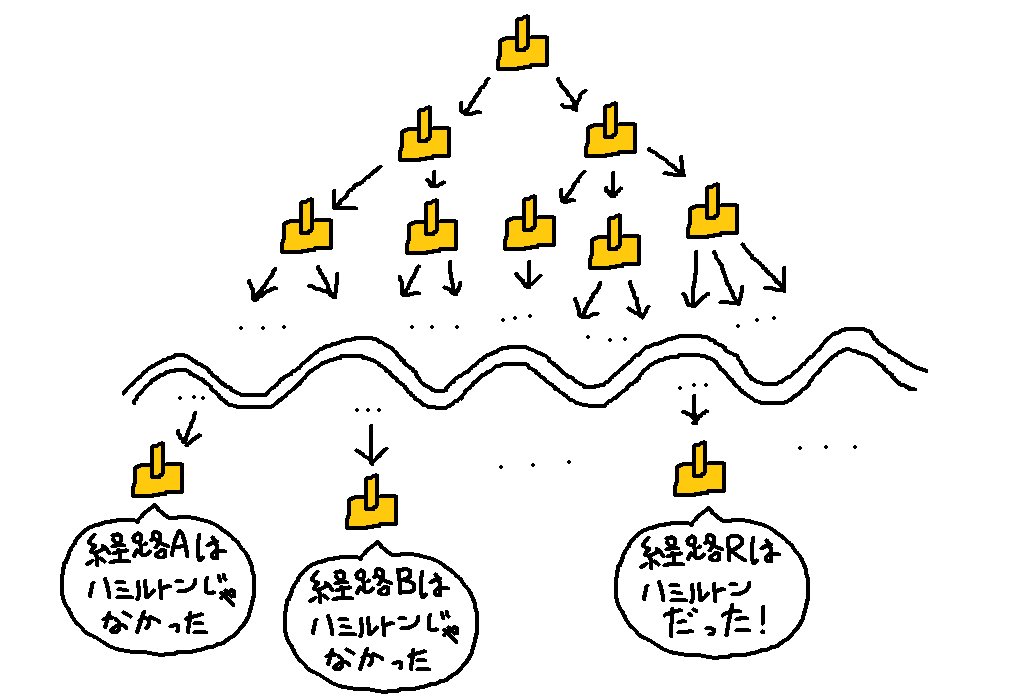
各分岐先の世界線でもさらに分岐は続いていきます。つまり非決定性チューリングマシンが計算を続ければ続けるほど、ねずみ算式に世界線が分岐していくことになります。

おびただしいほどに分岐していった世界線の内どれか一つでも受理状態で停止したならば非決定性チューリングマシンは入力を受理したということにしてしまいます。他の世界線は拒否状態で停止していたり、あるいは停止することなく永遠に動いていたとしても、たった一つでも受理状態で停止したならばそれでオッケーとしてしまうのです。

非決定性チューリングマシンのちゃんとした定義

非決定性チューリングマシン $T$ は七つ組 $\langle \Gamma, b, \Sigma, Q, q_{\mathrm{init}}, F, \delta \rangle$ です。基本的には決定性チューリングマシンと同じですが、遷移関数だけ定義が違います。

• $\delta$（遷移関数）：$\Gamma \times Q$ から $\mathcal{P}(\Gamma \times Q \times \{L, R\})$ への写像。

$T$ はヘッダから読み取れる文字 $c$、現在の状態 $q$ に対し、$\delta(c, q)$ が空でなければその元を任意に選んでテープの書き換え、状態の更新、テープの移動を行います。空だった場合は停止します。

$T$ が適切に状態遷移をすることによって受理状態で停止することが可能である、つまりそのような状態遷移の系列が一つでも存在したならば $T$ は入力を受理したといいます。またどのように状態遷移をしたとしても必ず拒否状態で停止してしまう場合 $T$ は入力を拒否したといいます。このどちらでもない場合、すなわち受理状態で停止する系列が一つも存在せず、なおかつ停止しない系列が一つ以上存在する場合 $T$ は入力に対し停止しないといいます。

さて、先ほど「ハミルトン閉路問題を効率的に解くには？」という話をしました。答えは可能な経路を一斉に確かめることでしたが、非決定性チューリングマシンを使えばそれができてしまいます。

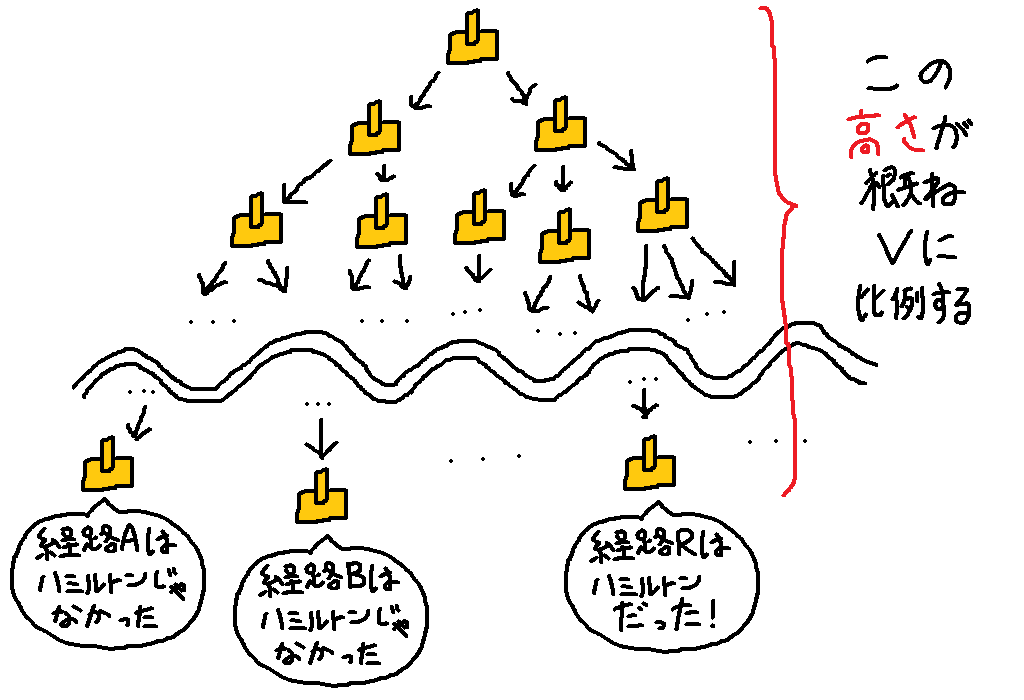
分岐していく世界線の一つひとつがそれぞれグラフ上の可能な経路に対応しています。なのでグラフの頂点数を $V$ とすると一つひとつの分岐は概ね $V$ に比例する長さを持つことになります。

非決定性チューリングマシンは全ての計算を一斉に進めていくので、したがってこの非決定性チューリングマシンは概ね $V$ に比例する計算時間で停止することになります。つまりハミルトン閉路問題は非決定性チューリングマシンを使えば計算時間を入力長の多項式で押さえつけれられるのです。このように「非決定性チューリングマシンを用いて入力長の多項式時間で解ける問題」を NP 問題といいます。"NP" は Non-deterministic Polynomial（非決定的多項式）の略です。ありがちな誤解なのが "NP" が Non-Polynomial の略だというものですが、これは明らかな誤りです。第一それだと P ≠ NP は自明ですし。

P 問題の定義は「決定性チューリングマシンを用いて入力長の多項式時間で解ける決定問題」でした。それに対し NP 問題は「非決定性チューリングマシンを用いて入力長の多項式時間で解ける決定問題」です。このように、「何らかの装置によってこれこれの時間計算量とこれこれの空間計算量で解ける問題の集合」を複雑性クラスといいます。代表例にはこんなのがあります。

• P: 決定性チューリングマシンによって入力長の多項式時間で解ける問題の集合
• NP: 非決定性チューリングマシンによって入力長の多項式時間で解ける問題の集合
• PSPACE: 決定性チューリングマシンによって入力長の多項式テープ長で解ける問題の集合
• NPSPACE: 非決定性チューリングマシンによって入力長の多項式テープ長で解ける問題の集合
• EXPTIME: 決定性チューリングマシンによって入力長の指数関数時間で解ける問題の集合
• R: チューリングマシンによって解ける問題の集合
• RE: Yes であれば必ず停止するが、No である場合停止するとは限らないチューリングマシンが解ける問題の集合
• RP: 入力長の多項式時間で解けるが、"Yes" という回答は確実に信用できる一方で "No" という回答は必ずしも信用できない問題の集合
• BQP: 量子コンピュータを用いて入力長の多項式時間で解ける問題のうち、誤り確率が 1/2 未満であるような問題の集合
• そのほか 500 個以上

P ≠ NP 問題は P 問題と NP 問題の関係を論じるものですが、P と NP 以外の複雑性クラスに関してもその包含関係はわからないことだらけです。これらを解き明かすことができればチューリング賞は確実でしょう。

P 問題と NP 問題の関係

「決定性チューリングマシン」と「非決定性チューリングマシン」を紹介しましたが、正直この二つのネーミングは誤解を招きます。「決定性チューリングマシン」と「非決定性チューリングマシン」は対義語であるかのように聞こえますが、それは違います。決定性チューリングマシンは非決定性チューリングマシンに含まれます。

非決定性チューリングマシンは状態遷移のたびに世界線が二つや三つに分岐するかもしれなかったわけですが、世界線が常に一つにしか分岐しない、要するに一切分岐を起こさない非決定性チューリングマシンも定義上はあり得ます。でもこれって要するに決定性チューリングマシンのことですよね。つまり決定性チューリングマシンは非決定性チューリングマシンの特殊な形なのです。いうなればりんご🍎と青りんご🍏の関係です。

さて、ここで P 問題と NP 問題の定義をおさらいしましょう。

• P 問題：決定性チューリングマシンを用いて入力長の多項式時間で解ける決定問題
• NP 問題：非決定性チューリングマシンを用いて入力長の多項式時間で解ける決定問題

そして今お話ししたように、決定性チューリングマシンは非決定性チューリングマシンの部分集合です。したがって、P 問題が NP 問題の部分集合であることは自明です。

しかし P 問題が NP 問題の部分集合であるとすると一つの疑問が残ります。すなわち、P 問題は NP 問題の真部分集合なのか、それとも実は P = NP なのか、ということです。これこそがまさに P ≠ NP 問題です。とうとう厳密なステートメントにたどり着きましたね！！

さっきは「非決定性チューリングマシンは世界線を分岐できる」など、非決定性チューリングマシンはとにかくすごいという話をしていました。しかし一つ誤解してはいけないことがあります。証明は省略しますが、非決定性チューリングマシンで解ける問題はすべて決定性チューリングマシンでも解けます。つまり決定性チューリングマシンで解ける問題の集合と非決定性チューリングマシンで解ける問題の集合は厳密に一致します。ただし両者は計算速度に関して天と地ほどの差がある（と思われている）ので、P ≠ NP 問題が生まれるわけです。

・・・で、どういうことだってばよ？

これまでの説明で P ≠ NP 問題のステートメントは飲み込んでいただけたと思いますが、こうお思いの方もいるかもしれません。

「う～ん、何を聞かれているのかは分かったけど、この問題の何がそんなに重要なのかピンと来ない・・・」

NP 問題は非決定性チューリングマシンで解ける問題でしたが、そもそもこの「非決定性チューリングマシン」というのが余りにも現実離れした存在です。だって現実のコンピュータで世界線を分岐させるなんてできないじゃないですか。並列計算を使えば真似事のようなことはできますが、1 台のコンピュータが利用可能なスレッドの数なんてたかが知れています。非決定性チューリングマシンのようにねずみ算式に増えていく計算には到底追いつけません。そんな「現実離れした機械」で解ける問題なんて言われてもいや知らんわ、って感じでしょう。

ですがご安心ください。NP 問題にはもう一つの定義が存在します。厳密な内容は今からゆっくりご説明しますが、かみ砕いたバージョンを今お見せするとこのようになります。

NP 問題とは、検算が P 問題である問題のことである。

回答を検証するということ

ここで皆さまに問題です。このグラフにハミルトン閉路が存在することを証明してください。

ハミルトン閉路が存在する簡潔な必要十分条件は知られていないのでエレガントな証明は難しそうです。しかし手探りで実例を探し出すのはさすがに無理がありますし、かといってプログラムで解くのも時間がかかりすぎます。

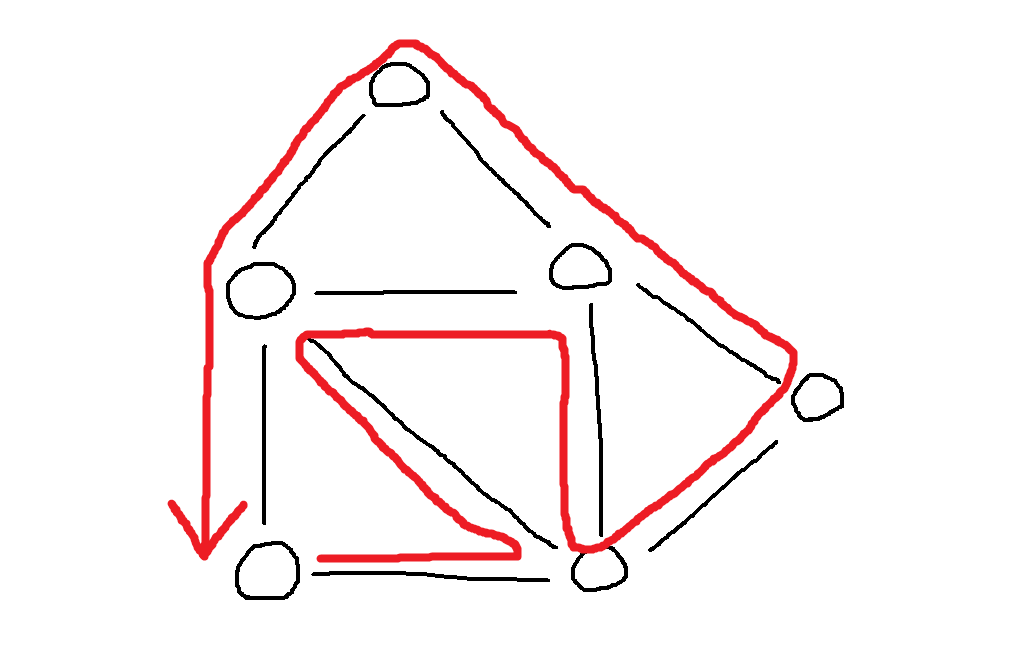
ですがこちらの問題であればどうでしょう。以下に示す経路がハミルトン閉路であることを確かめてください。

ハミルトン閉路の存在証明はとても難しいことですが、しかし与えられた経路がハミルトン閉路であることを確かめるのは容易いことです。ただ与えられた経路内にすべての頂点がちょうど 1 回ずつ現れることとスタート地点まで戻ってくることだけを確かめればいいので、明らかに決定性チューリングマシンを使って多項式時間で解ける問題、すなわち P 問題ですよね。

さて、こちらの問題では「ハミルトン閉路の実例」が最初から示されていました。つまり「グラフ上にハミルトン閉路が存在すること」の証拠が最初から与えられているのです。そしてその証拠が本当にまっとうなのかどうかは、先ほども述べたようにチューリングマシンを用いて確かめられます。このように、「証拠がまっとうなのかどうか」確かめることを検証といいます。我々が今示そうとしているのは​「問題 $X$ が NP 問題であること」と「問題 $X$ の検証が P 問題であること」は同値であるということです。もう少し厳密に見ていきましょう。

ここにハミルトン閉路問題を解ける非決定性多項式時間チューリングマシン $H$⁷ があるとします。すなわち $H$ は「ハミルトン閉路を持つグラフを表現した文字列」のみをすべて受理し、そうでない文字列を全て拒否します。このとき検証機械 $V$⁸ は次のように定められます。

文字列 $S$ が $H$ によって受理されるならば $S$ に対する適当な証拠 $W_S$⁹ が存在し、$V$ も $S$ と $W_S$ を受理する。

逆に $S$ が $H$ によって拒否されるならば $V$ はいかなる $W$ に対しても $S$ と $W$ を拒否する。

「・・・？」という方もいるでしょう。もうちょっと丁寧に見ていきましょう。

まず文字列 $S$ が $H$ によって受理される、すなわち $S$（によって表現されるグラフ）はハミルトン閉路を持つとします。このとき $S$（によって表現されるグラフ）内に含まれるハミルトン閉路そのものが、$S$ が $H$ によって受理されることの証拠となります。この実在するハミルトン閉路そのものを適当な方法で文字列に書き起こしたものを証拠 $W_S$ とします。

さて、検証機械 $V$ への入力となるのは $S$ と $W_S$ です。このとき検証機械 $V$ は $W_S$ が「本当に証拠になっているかどうか」を検証します。具体的には先ほども見たように「$W_S$ が示す経路内にすべての頂点がちょうど 1 回ずつ現れること」と「スタート地点まで戻ってくること」だけ確かめればよいです。

次に、$S'$ を $H$ に受理されない文字列とします。すなわち $S'$（によって表現されるグラフ）はハミルトン閉路を持たないとします。こうなると検証機械 $V$ はいかなる文字列 $W$ に対しても $S'$ と $W$ を拒否することになります。そもそもハミルトン閉路が一つも存在しない以上「ハミルトン閉路の実例」を示すことは不可能ですし、そうなるといかなる文字列も「証拠」たりえないからです。

これで「検証」とはいったい何なのかお判りいただけたでしょうか。最初は少し混乱するかもしれないので、一旦立ち止まって頭を整理するといいと思います。

さてここで一旦振り返ります。我々が今示そうとしているのは、​「問題 $X$ が NP 問題であること」と「問題 $X$ の検証が P 問題であること」は同値である、ということでした。すなわち我々が示したいのは以下の二つです。

• 任意の NP 問題に対し決定性多項式時間検証機械が存在する。
• 決定性多項式時間検証機械が存在する問題は NP 問題である。

ここで一つ注意事項があります。それは、多項式時間検証機械に入力される「証拠」の長さについてです。

ハミルトン閉路問題を解く非決定性チューリングマシン $H$ は入力 $S$ に対して入力長の多項式時間、すなわち $|S|$¹⁰ の多項式時間で停止したわけですが、多項式時間検証機械にもこれと同じことが求められます。つまり、多項式時間検証機械もまた $|S|$ の多項式時間で停止しなければならないのです。検証機械への入力は $S$ と $W_S$ だったわけですが、多項式時間検証機械はあくまでも $|S|$ の多項式時間で停止しなければならないことに注意してください。

ここで $S$ に対する証拠である $W_S$ が $S$ に対してものすごく長かったとします。そうですね、例えば $W_S$ が $|S|!$ と同程度の長さだったとします。検証機械 $V$ は $S$ と $W_S$ を適当に連結した文字列を受け取るわけですが、$|W_S|$ が $|S|!$ 程度なわけですから入力の長さも $|S|!$ 程度にはどうしてもなってしまうでしょう。すると、どう考えても $V$ は入力のすべての文字を読み切ることはできないですよね？言うまでもないことですが、入力のすべての文字を読み切るには最短でも入力の文字数分の時間がかかるわけですから。

つまり $V$ が多項式時間で止まらなければならない以上、「証拠」の長さも必然的に制限を受けることになるのです。すなわち、$|W_S|$ は $|S|$ の多項式で押さえつけられなければなりません。そういうわけで決定性多項式時間検証機械に求められることをまとめておきましょう。

文字列 $S$ が $H$ によって受理されるならば $S$ に対する適当な証拠 $W_S$ が存在し、$V$ も $S$ と $W_S$ を $|S|$ の多項式時間で受理する。ただし $|W_S|$ は $|S|$ の多項式で抑えられなければならない。

逆に $S$ が $H$ によって拒否されるならば $V$ はいかなる $W$ に対しても $S$ と $W$ を $|S|$ の多項式時間で拒否する。

おわかりいただけましたか？オーケイ、それでは次に行きましょう。

⇒

いままで「NP 問題であること」と「検証が P 問題であること」は同値だ、と主張してきたわけですが、その証明を今からします。まずは右向きの証明、すなわち NP 問題の検証は P 問題であることを証明します。

ハミルトン閉路問題とそれを解く非決定性チューリングマシン $H$ にまた登場してもらいましょう。$H$ はこんな風に動作していました。

可能な経路の全てを同時に確認し、ハミルトン閉路が存在するか調べます。頂点数 $V$ に対し一つひとつの分岐はせいぜい $V$ の 1 次式程度の長さしか持たないため、$H$ は入力長の多項式時間で停止するという議論でした。

さて、もし仮にハミルトン閉路が存在していたとすると分岐していった世界線のうち最低でも 1 本は受理状態で停止しています。逆にハミルトン閉路が存在しなかった場合、受理状態で停止する世界線は 1 本もありません。すべての世界線は拒否状態で停止しています。

・・・なにかピンと来ませんか？そう、この $H$ が受理状態で停止する世界線自体がハミルトン閉路が存在することの証拠として使えそうじゃないですか？

ここで $S$ に対する証拠 $W_S$ に課される条件を思い出してみましょう。

• $W_S$ は $S$ が $H$ に受理されるときにのみ必ず存在し、なおかつ $|W_S|$ は $|S|$ の多項式で押さえつけられなければならない。

では $S$ が $H$ によって受理される世界線、もっと具体的に言えば $H$ が $S$ を受理するに至る状態遷移の系列について考えましょう。

• 「$H$ が $S$ を受理するに至る状態遷移の系列」は $S$ が $H$ に受理されるときにのみ必ず存在し、なおかつその系列の長さは（$H$ が入力長の多項式時間で停止するので）$|S|$ の多項式で押さえつけられる。

よって「$H$ が $S$ を受理するに至る状態遷移の系列」は「$H$ が $S$ に受理されることの証拠」の条件を完璧に満たしています。そこで、この「$H$ が $S$ を受理するに至る状態遷移の系列」を適当に文字列として書き起こしたものを証拠 $W_S$ と置きます。このとき決定性多項式時間検証機械 $V_P$ は $S$ と $W_S$ を受け取り、「$H$ が $S$ を入力として受け取ったとき、$W_S$ によって示される状態遷移は本当に可能なのか」を検証します。この検証は $W_S$ によって示される状態遷移の系列を先頭から順番に確かめるだけなので明らかに $|W_S|$ に比例する時間で終わらせられます。また、先ほど示したように $|W_S|$ は（$H$ が多項式時間チューリングマシンなので）$|S|$ の多項式で押さえつけられます。よって $V_P$ による検証は $|S|$ の多項式時間で終了するので、命題「NP 問題の検証は P 問題である」が証明されました。

⇐

それでは今度は逆向きの証明です。すなわち、検証が P 問題である問題は NP 問題であることを証明します。

ここにハミルトン閉路問題の決定性多項式時間検証機械 $V_P$ があるとします。$V_P$ は文字列 $S$ と証拠 $W_S$ を受け取り、$W_S$ がまっとうな証拠であるならば受理状態で停止し、そうでなければ拒否状態で停止します。

さて、ここでハミルトン閉路問題を解く非決定性チューリングマシン $H$ に文字列 $S$ が入力されたとします。今証明したいことは「検証が P 問題である問題は NP 問題である」、言い換えれば「決定性多項式時間検証機械が存在する問題は非決定性チューリングマシンを用いて多項式時間で解ける」ということなので、$V_P$ さえ存在していれば $H$ はどうにかして多項式時間で停止できる、ということさえ示せればよいです。要するに $H$ は $V_P$ に協力してもらってハミルトン閉路問題を多項式時間で解くのです。具体的には何をするのでしょうか？

ここでいくつかおさらいします。まず $V_P$ が受理状態で停止するのは $S$ がハミルトン閉路付きグラフを表現している証拠が存在するときのみでした。よってそのような証拠が見つかったなら $S$ はハミルトン閉路付きグラフを表現していると胸を張って言えます。また逆に、そのような証拠が一つも見つからなかったならば $S$ はハミルトン閉路付きグラフを表現していないと断言できます。

そしてもうひとつおさらいしたいのが、非決定性チューリングマシンは「複数の可能性を同時に検証できる」ということです。ハミルトン閉路問題を一斉に総当たりして解いたように、あらゆる可能性を一斉に検証するのは非決定性チューリングマシンの得意とするところです。

もうお判りいただけたでしょうか。$H$ は $V_P$ が $S$ を受け入れてくれるような証拠を一斉に総当たりするのです。つまり、$H$ は「文字列 "abcccdd" は $S$ がハミルトン閉路付きグラフを表現している証拠になるかな？」「文字列 "d82hf8sa" は $S$ がハミルトン閉路付きグラフを表現している証拠になるかな？」「文字列 "cj90dqj0dqwfjq0fqf" は $S$ がハミルトン閉路付きグラフを表現している証拠になるかな？」という風に、ありとあらゆる証拠のすべてをしらみつぶしに $V_P$ に入力していきます。最終的に $V_P$ が受理状態で停止するような「証拠」が見つかったなら $H$ も受理状態で停止し、そうでなければ $H$ は拒否状態で停止します。

「・・・え？でも『証拠』になりうる文字列は無限に存在するんじゃないの？」と思う方もいらっしゃるかもしれません。しかし、$S$ に対する証拠 $W_S$ に課される条件を思い出してください。

$|W_S|$ は $|S|$ の多項式で押さえつけられなければならない。

これはもう少し厳密な言い方をするとこのようになります。

とある多項式 $p(\cdot)$ が存在し、任意の文字列 $S$ に対し $S$ に対する証拠 $W_S$ の長さは $p(|S|)$ 以下でなければならない。

よって、「証拠」をしらみつぶしに探すにあたって無限の文字列のすべてを取り扱う必要はありません。探索範囲にするのは長さが $p(|S|)$ 以下の文字列だけで十分なのです。この範囲で証拠が見つからなければ $S$ はハミルトン閉路付きグラフを表現していないと断言できます。したがって、命題「検証が P 問題である問題は NP 問題である」が証明できたので、先ほどの証明と組み合わせて「NP 問題であることと検証が P 問題であることは同値である」と証明できました。

第 3 部：P ≠ NP 問題の重要性

「NP 問題であることと検証が P 問題であることは同値である」と証明されたので、命題 "P = NP" はざっくりとこのように言い換えることができます。

現実世界のコンピュータにおいて、多項式時間で検算できる問題は多項式時間で解ける。

誤解を恐れずにさらにかみ砕けばこういうことになります。

検算が簡単な問題は解くのも簡単である。

もし P = NP が真であった場合何がヤバい（かもしれない）かというと、真っ先に挙げられるのが暗号分野の話題です。RSA 暗号に代表される一部の暗号方式の安全性は「素因数分解の困難さ」に依拠しています¹¹が、もし P = NP だと入力長の多項式時間で素因数分解を行うアルゴリズムがどこかに存在することになります。以下もう少し詳しく見てみましょう。

「え？ $N$ の素因数分解って $N$ の多項式時間でできない？」とお思いの方もいるかもしれません。

import math

N = int(input())
sqrtN = int(math.ceil(math.sqrt(N)))
factors = []

for factor in range(2, sqrtN + 1):
    degree = 0
    while N % factor == 0:
        N //= factor
        degree += 1
    if degree != 0:
        factors.append([factor, degree])
if N != 1:
    factors.append([N, 1])

print('*'.join([f'{factor}^{degree}' for (factor, degree) in factors]))

このアルゴリズムは入力された自然数 $N$ に対し概ね $\sqrt{N}$ に比例する計算時間で素因数分解を行うので、計算時間は $N$ の多項式時間です。

しかし思い出してほしいのが、P 問題は入力長の多項式時間で解けなければならないということです。この場合入力長というのは $N$ という値ではなく、$N$ の桁数に当たります。$N$ が $r$ 進法で表記されているとすると $N$ の桁数は概ね $\log_r{N}$ になります。よってこのアルゴリズムの計算時間は概ね $\sqrt{N} = \sqrt{r^{\log_r{N}}} = r^{\frac{\log_r{N}}{2}}$ に比例します。つまり入力長の指数関数時間になってしまっているので、素因数分解を多項式時間で解けることを示したことにはなりません。

今回示したアルゴリズムのように入力された値（入力長ではなく）の多項式時間で問題を解くアルゴリズムを擬多項式時間アルゴリズムといいます。あくまでも「擬」がつくことに注意してください。

まず詳細は省きますが、「素数判定」は NP 問題です。つまり自然数 $N$ と「$N$ が素数である証拠」を入力として受け取り、その証拠が本当にまっとうであるか検証する決定性多項式時間検証機械が存在します。「素数である証拠」としてどんなものがあるのかはこちらを参照してください。

さらに実をいうと素数判定は P 問題でもあります。インド工科大学の研究チームが実際に入力長の多項式時間で素数判定を行うアルゴリズム（AKS 素数判定法）を開発しています。¹²

さて素数判定が NP 問題であることから以下の問題も NP 問題です。

自然数 $N$ は $k$ 以下の素因数を持つか否か？

この問題の検証機械は $N$、$k$、そして証拠として「$N$ の $k$ 以下の約数の実例」と「その実例が素数である証拠」を受け取ります。この検証機械が確かめるべきことは

• 「実例」が $k$ 以下であること
• 「実例」が $N$ を割り切ること
• 「実例」が素数であること

だけですが、このすべてが多項式時間で決定的に検証可能です。よって NP 問題であることが示されました。したがってもし仮に P = NP であったならばこの問題「自然数 $N$ は $k$ 以下の素因数を持つか否か？」も当然 P 問題ということになってしまうので、二分探索の要領で「$N$ の素因数のうち最小のもの」を探し当てることができます。二分探索は概ね $\log_2{N}$ に比例する計算時間がかかりますが、これは $N$ の桁数、すなわち入力長に比例する計算時間になります。よって $N$ の素因数を小さい方からどんどん探していき、見つかり次第 $N$ を割り続けることで素因数分解を実現できます。

まとめると、もし P = NP であるならば素因数分解を決定性チューリングマシンを用いて、すなわち現実に存在するコンピュータを用いて多項式時間で解く方法がどっかしらに存在していることになってしまうので、暗号の安全性の保障が消えてなくなってしまうのです。

第 4 部：P ≠ NP 問題・解決への道

これで P ≠ NP 問題のステートメント、およびその重要性はなんとなく分かっていただけたと思います。ではこの P ≠ NP 問題はどうすれば解決できるのでしょうか？

P 問題が NP 問題の部分集合であることは自明だったわけですから、P ≠ NP の証明には「P 問題ではない NP 問題」を一つでも挙げればよいです。つまり、「非決定性チューリングマシンでは多項式時間で解けるけど決定性チューリングマシンでは絶対に多項式時間で解けない問題」を一つでも見つけ出すことができれば P ≠ NP を証明したことになります。もちろんこれは口で言うほど簡単ではありませんが、すくなくとも一つの方針にはなります。

また別の証明法もあります。ある決定問題の Yes / No をひっくり返した問題をその決定問題の補問題といい、そして複雑性クラス C の決定問題の補問題の集合を co-C といいます。ここで P = NP を仮定すると、当然のことながら co-P = co-NP になります。また P = co-P は自明なので、ここから P = NP ならば NP = co-NP といえます。この対偶を取って NP ≠ co-NP ならば P ≠ NP を得ます。

それでは P = NP の証明はどうすればよいでしょうか？ P = NP を証明するとはつまり「全ての NP 問題は P 問題である」ことを証明することになりますが、しかし NP 問題は無数に存在します。NP 問題一つひとつに対して多項式時間アルゴリズムを見つけ出すなんてことをしていたら日が暮れるどころの騒ぎではありません。それではもし仮に P = NP であったとしてもその証明は不可能なのでしょうか？

いいえ、実は P = NP の証明には起死回生の一手が存在します。

「帰着」

まずこんな有名な問題があります。

巡回セールスマン問題：

いくつかの都市および各都市間の距離が与えられるので、全ての都市をちょうど 1 度ずつ回ってスタート地点に戻ってくる最短経路の距離を求めよ。

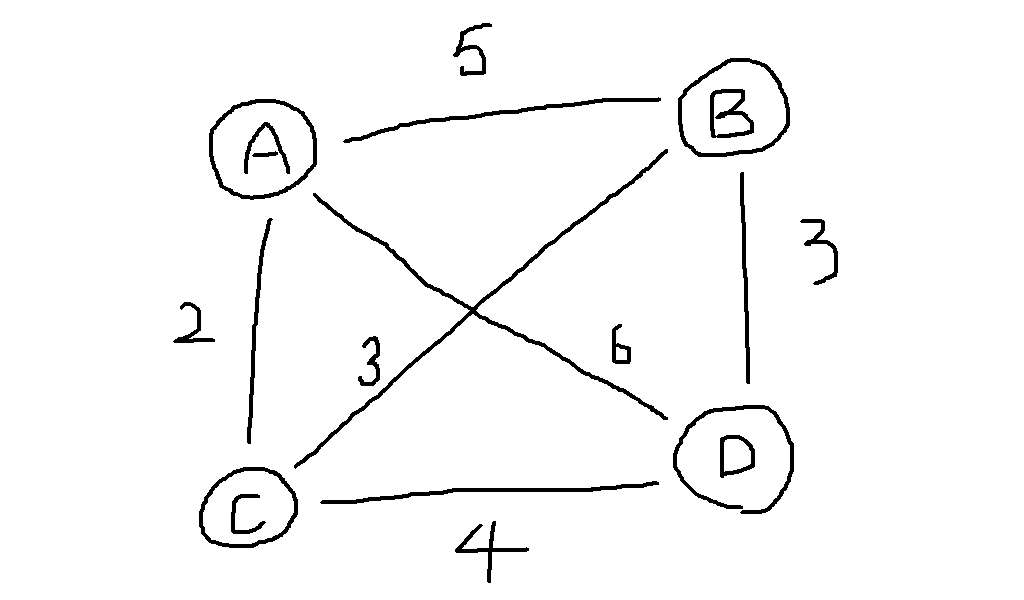
もうちょっと厳密なステートメント：重み付き完全グラフが与えられるので、すべての頂点をちょうど 1 度だけ含む閉路の長さの最小値を求めよ。

例として下図に示す地図では A → C → B → D → A という経路が条件を満たす最短経路なので、回答は 14 になります。

さて今までさんざん登場してもらったハミルトン閉路問題ですが、重み無しグラフ $G$ の頂点数を $V$ とすると $G$ 上の閉路がハミルトン閉路である必要十分条件はその閉路の長さが $V$ で全ての頂点を含むことです。よってこのハミルトン閉路問題は以下のように言い換えることができます。

グラフ $G$ の各辺の重みを 1 とする。また $G$ が完全グラフになるように辺を追加する。ただし追加された辺の重みは 1 より大きい任意の数とする。こうして作った完全グラフに対する巡回セールスマン問題の解は $G$ の頂点数と一致するか？

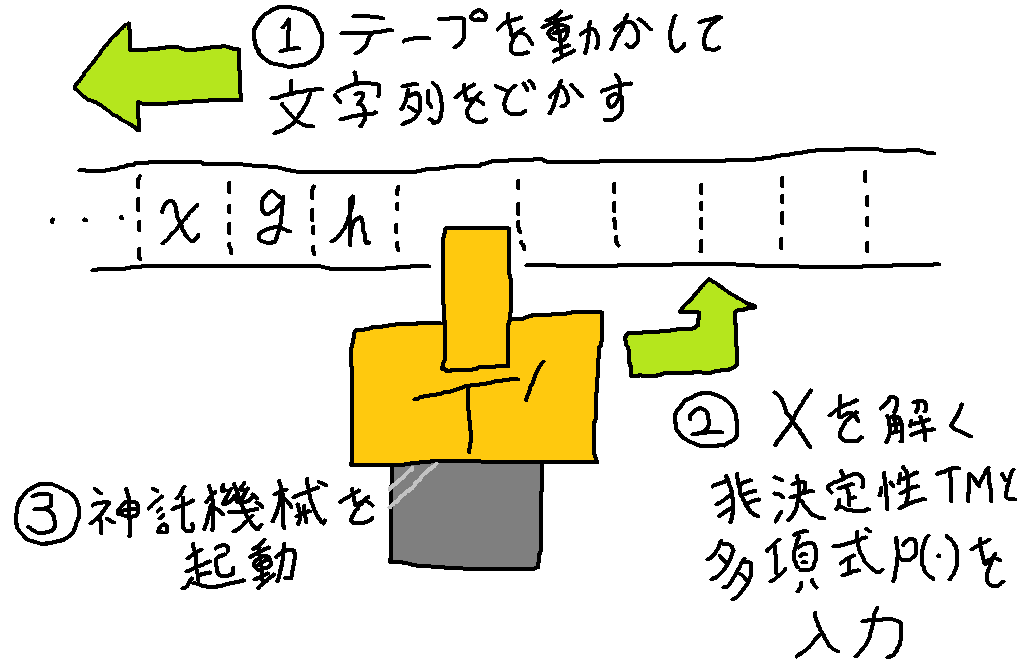
細かい話は抜きにして、要するに巡回セールスマン問題が解けるならばハミルトン閉路問題も解けるということになります。より具体的にはこのようなチューリングマシンを使ってハミルトン閉路問題を解きます。

チューリングマシンになにやら得体の知れない箱がくっついています。この箱も一種のチューリングマシンなのですが、ある一つのとんでもない仮定を置いています。すなわち、この「箱」は巡回セールスマン問題を 1 ステップで解くことができるのです。

どういうことかというと、ふつう巡回セールスマン問題をチューリングマシンで解くならば「状態を遷移して、テープを書き換えて、また状態を遷移して、またテープを書き換えて・・・」というふうに 1 ステップずつ地道に答えに近づいていくものなのですが、「箱」はこの全てを 1 ステップで終わらせることができてしまう（と仮定されている）のです。つまりこの「箱」は、あたかも全知全能の神から答えを教えてもらったかのようにふるまいます。この「箱」をオラクル、日本語では神託機械といいます。ネーミングかっこよすぎない・・・？

さて先ほど図に示した「神託機械付きチューリングマシン」がハミルトン閉路問題をどのようにして解くのか解説します。入力としてグラフ（を表現した文字列）を受け取ったチューリングマシンはまずグラフの頂点数をカウントします。このカウント結果をテープ上の適当な位置に控えておきます。次にグラフを上で述べたように適切に完全グラフへと「変形」したのち、神託機械を起動します。神託機械は巡回セールスマン問題を 1 ステップで解いてしまうので、神託機械が仕事を終えた後テープ上には巡回セールスマン問題の解、すなわち「全ての頂点をちょうど 1 度ずつ回ってスタート地点に戻ってくる最短経路の距離」が書き込まれています。あとはこれをさっき控えておいた頂点数と比較し、一致すれば答えは Yes、一致しなければ答えは No です。このように「問題 $B$ に回答する神託機械を併設したチューリングマシンが問題 $A$ を解ける」ことを「問題 $A$ は問題 $B$ へとチューリング帰着可能である」といいます。問題 $A$ が問題 $B$ にチューリング帰着可能であるとは「$B$ さえ解ければ $A$ も解ける（逆は必ずしも成り立たない）」という意味なので、直観的に「$B$ は $A$ 以上に難しい」といえます。

NP 完全問題

問題 $A$ が問題 $B$ にチューリング帰着可能であるとき、問題 $A$ を解くチューリングマシンは入力を変形したのち問題 $B$ を解く神託機械を起動していました。そして上で見たようなハミルトン閉路問題から巡回セールスマン問題への帰着の場合、入力文字列の「変形」は決定性チューリングマシンを用いて多項式時間で終わらせられますし、その後神託機械と協力しながら行っていく計算もやはり決定性チューリングマシンを用いて多項式時間で終わらせられます。このように、問題 $B$ に回答する神託機械の助けを得ることを許したうえで決定性チューリングマシンが問題 $A$ を多項式時間で解けるとき、問題 $A$ は問題 $B$ へと多項式時間チューリング帰着可能であるといいます。すなわちハミルトン閉路問題は巡回セールスマン問題に多項式時間チューリング帰着可能ということになります。

ここで、任意の NP 問題から多項式時間チューリング帰着可能な NP 問題の存在を仮定します。つまりこんな感じです。

NP 問題は無数に存在するわけですがそのすべてがたった一つの NP 問題に多項式時間チューリング帰着可能であると仮定します。もし仮にこの問題が決定性チューリングマシンを用いて多項式時間で解ける、すなわち P 問題であったならば全ての NP 問題もまた P 問題であることになります。なぜなら P 問題に多項式時間チューリング帰着可能な問題は明らかに P 問題だからです。そして「全ての NP 問題が P 問題である」とはすなわち P = NP であるということです。よってこのような究極の NP 問題の存在を仮定することで P = NP 証明の足掛かりが得られるのです。この究極の NP 問題を NP 完全問題といいます。

より一般に、複雑性クラス C に属する任意の問題からチューリング帰着可能な C 問題を C 完全問題といいます（通常、ここで行われるチューリング帰着は高々 C 問題程度の複雑さであるという暗黙の了解が置かれます）。

・・・しかし、NP 問題は無数に存在します。そのすべてから多項式時間チューリング帰着可能な問題などという都合がよすぎる問題など本当に存在するのでしょうか？

自明な例

「すべての NP 問題から多項式時間チューリング帰着可能な NP 問題を示せ」と言われても、とっかかりがなさすぎて困ってしまいます。しかし冷静に考えてみれば明らかに NP 完全である問題が一つあります。こんな問題です。

非決定性チューリングマシン $T$ を表現した文字列と、多項式 $p(\cdot)$ を表現した文字列と、$T$ への入力文字列 $S$ が与えられたとき、$T$ は $S$ に対して $p(|S|)$ ステップ以内に受理状態で停止するか判定せよ。

この問題が NP 完全であることを証明するには以下の二つを確かめればよいです。

• 任意の NP 問題が、この問題に回答する神託機械を併設した決定性チューリングマシンによって多項式時間で解けること。
• この問題自体が NP 問題であること。

まず一つ目からです。この問題に回答する神託機械を併設した決定性チューリングマシン $T'$ は以下のようにして NP 問題 $X$ に回答します。

$T'$ のテープには $X$ への入力が書き込まれているわけですが、まず $T'$ はテープを「ガーッ！」っと動かし、入力文字列をどかしてしまいます。その後 $T'$ は「多項式時間で $X$ を解く非決定性チューリングマシンを表現する文字列」と「$X$ を解くのにかかる時間を押さえつける多項式 $p(\cdot)$」をテープに書き込みます。さっき入力文字列をどかしておいたのは上書きを防ぐためだったのです。あとは神託機械を起動してやれば解きたかった NP 問題の解が得られるという寸法です。

ここでこの計算にかかる時間を見積もります。$T'$ がやることは「入力文字列をどかすこと」と「多項式時間で $X$ を解く非決定性チューリングマシンを表現する文字列を書き込むこと」と「$X$ を解くのにかかる時間を押さえつける多項式 $p(\cdot)$ を書き込むこと」だけです。入力文字列をどかす方はどう考えても入力文字列の長さに比例する時間で終わらせられます。またチューリングマシンと多項式を書き込む方ですが、こちらは「テープの中身」には関係なく定まるので長さは定数になります。なので結局総計算時間は「テープの中身」の長さの 1 次関数で押さえつけられることになります。よって任意の NP 問題はこの問題に多項式時間チューリング帰着可能ということになるので、あとはこの問題自体が NP 問題であることを示せば NP 完全であることを示したことになります。

NP 問題であることはほとんど自明です。実際に $T$ に $S$ を入力し、状態遷移の回数が $p(|S|)$ を超えた時点で計算を打ち切って拒否状態で停止してしまえばよいからです。よって NP 完全問題であることが示されました。

充足可能性問題

これで NP 完全な問題の例が一つ示されたわけですが、しかしこの例はあまりにも自明すぎてほとんど意味がないように思われます。ですがここで一つ重要な事実が存在します。NP 完全問題の定義より、NP 完全問題から多項式時間チューリング帰着可能な NP 問題もまた NP 完全問題なのです。なので先ほど示した「自明な NP 完全問題」から多項式時間チューリング帰着可能な NP 問題もまた NP 完全問題です。その代表例が充足可能性問題です。

充足可能性問題とは論理式を真にするような真偽値の割り当ての存在を問う問題です。例えば論理式 $P \land \lnot Q \land (R \lor S)$ について考えます。この式全体を真にするにはどのように $P, Q, R, S$ を定めればよいでしょうか？

一例としては $P, R$ を真、$Q, S$ を偽とするという割り当てが考えられます（もちろんほかにも割り当て方はあります）。よって与えられた論理式は全体を真にすることが可能です。このことを充足可能といいます。

他の例として論理式 $P \land (Q \land R \land \lnot Q)$ について考えます。この論理式は充足可能でしょうか？

・・・はい、この論理式はどうあがいても真にすることはできません。$P, Q, R$ にどのような真偽値を定めても式の値は必ず偽になってしまいます。このことを充足不能といいます。

このように、与えられた論理式が充足可能であるか否か回答する問題を充足可能性問題といいます。

「充足可能性問題が NP 完全問題である」という定理は Cook-Levin の定理と呼ばれます。これを証明するには、充足可能性問題が先ほど示した「自明な NP 完全問題」から多項式時間チューリング帰着可能であることを示せばよいです。「自明な NP 完全問題」はこんなのでした。

非決定性チューリングマシン $T$ を表現した文字列と、多項式 $p(\cdot)$ を表現した文字列と、$T$ への入力文字列 $S$ が与えられたとき、$T$ は $S$ に対して $p(|S|)$ ステップ以内に受理状態で停止するか判定せよ。

このとき $T$ が $p(|S|)$ ステップ以内に $S$ を受理するならば充足可能で、そうでなければ充足不能な論理式をどうにかして構成することが可能（らしい）です。こんな感じのノリで充足可能性問題が NP 完全であることを証明できるそうです。詳しいことは知らん

さて充足可能性問題は「自明な NP 完全問題」から多項式時間チューリング帰着可能な NP 問題であるので NP 完全問題でした。以下同様にして「充足可能性問題から多項式時間チューリング帰着可能な NP 問題」、「その問題から多項式時間チューリング帰着可能な NP 問題」、「その問題から多項式時間チューリング帰着可能な NP 問題」・・・もすべて NP 完全問題です。このようにして NP 完全問題は芋づる式に見つかっていくのです。具体的な帰着の仕方は省略しますが、以下の問題は全て NP 完全です。この中のどれか一つでも多項式時間で解ければ 1 億 4000 万円が手に入ります。

• 充足可能性問題：与えられた論理式は充足可能か？
• ハミルトン閉路問題：与えられたグラフにハミルトン閉路は存在するか？
• 巡回セールスマン問題（決定問題バージョン）：与えられた重み付き完全グラフに長さ $k$ 以下ですべての頂点を含む閉路は存在するか？
• テトリス¹³
• ぷよぷよ¹⁴
• etc. ...

これまで大活躍してもらったハミルトン閉路問題は実のところ NP 完全でした。なんとこのときのための伏線だったんですね～。

NP 困難問題

NP 完全に似た概念に NP 困難というものがあります。NP 困難問題は「任意の NP 問題から多項式時間チューリング帰着可能な決定問題または関数問題」です。関数問題とは何だったか覚えてますか？決定問題が「Yes / No で答えられる問題」で、それ以外の問題が関数問題でした。つまり NP 困難は NP 完全より広い概念です。「NP 完全問題とは NP 困難であるような NP 問題のことである」とも定義できます。

より一般に、複雑性クラス C に属する任意の問題からチューリング帰着可能な問題を C 困難問題といいます（ここでもやはりチューリング帰着は高々 C 問題程度の複雑さであるという暗黙の了解が置かれます）。そして C 困難であるような C 問題を C 完全問題といいます。

NP 困難問題の例としては以下が挙げられます。

• 巡回セールスマン問題：セールスマンが町を回るのにどれくらい時間がかかるか
• ナップサック問題：遠足にどれくらいいっぱいおやつを持っていけるか
• 停止性問題（そもそも決定不能なんだから帰着させる意味は薄いけど）
• スーパーマリオブラザーズ¹⁵
• ドンキーコング¹⁵
• ゼルダの伝説¹⁵
• メトロイド¹⁵
• ポケットモンスター¹⁵
• etc. ...

NP 完全問題と同様、NP 困難問題も多項式時間で解ける方法を考案できれば P = NP を証明したことになります。

おわりに ～ P = NP は本当にヤバいことか？ ～

さて、長い長い記事になりましたがそろそろおしまいにしたいと思います。ここまで読んでくださり本当にありがとうございます。最後に、P ≠ NP 問題が社会にもたらす影響についてちょっと考察したいと思います。

仮に P = NP である場合、一部の暗号技術の安全性が破られる「かもしれない」のでヤバいというお話をしましたが、果たして本当にそのようなことが起こるでしょうか？

NP 問題にはこの記事で何度も登場したハミルトン閉路問題を始め無数の問題が含まれます。仮に P = NP であれば、その無数の問題の全てが多項式時間で解けることがいきなり判明することになります。それはさすがにちょっとあり得ないのではないでしょうか？

もちろん人類は全知全能ではないですし、我々が想像もつかないようなアルゴリズムが存在する可能性は捨てきれません。ただここで思い出してほしいのが、P = NP が証明されたからといって多項式時間アルゴリズムが見つかるとは限らないし、仮に本当に多項式時間アルゴリズムが見つかったとしてもそのアルゴリズムが短時間で終了するとは限らないということです。少し前にも出した例えですが、入力長の 1 兆乗に比例する計算時間がかかる問題も定義からいえば立派な P 問題なのです。

ですから、「素因数分解を多項式時間で実施するアルゴリズムが発見されました。ただし計算時間は入力長のグラハム数乗に比例します」なんてオチもあり得るわけです。なのでもし P = NP が証明されたとしてもそれがすぐに世界の混乱に直結するとは限らないのです。

最後に、著名な計算機科学者ドナルド・クヌースの言葉を引用したいと思います¹⁶。クヌースは P = NP と予想しているのですが、その考えについて質問されたときの返答です。

（前略）

原文：My main point, however, is that I don't believe that the equality P = NP will turn out to be helpful even if it is proved, because such a proof will almost surely be nonconstructive.

拙訳：しかしながら私が一番言いたいのは、仮に P = NP だとしてもその事実が役に立つとは思えないということです。なぜなら P = NP の証明はほぼ間違いなく非構成的¹⁷でしょうから。

（中略）

Mathematics is full of examples where something is proved to exist, yet the proof tells us nothing about how to find it. Knowledge of the mere existence of an algorithm is completely different from the knowledge of an actual algorithm.

数学には対象の存在は示すものの、その見つけ方については何も語らない証明がいっぱいあります。あるアルゴリズムがただ存在しているとだけ知っていることと、そのアルゴリズムを実際に知っていることとは全く別のことです。

For example, RSA cryptography relies on the fact that one party knows the factors of a number, but the other party knows only that factors exist. Another example is that the game of N × N Hex has a winning strategy for the first player, for all N. John Nash found a beautiful and extremely simple proof of this theorem in 1952. But Wikipedia tells me that such a strategy is still unknown when N = 9, despite many attempts. I can't believe anyone will ever know it when N is 100.

例えば RSA 暗号は、一方は約数を実際に知っており、他方は約数が存在していることだけを知っているという事実に依拠しています。他にも例を挙げると、N × N のヘックス¹⁸は全ての N に対し先手必勝の戦略が存在します。この事実の美しく、そして極めて簡潔な証明がジョン・ナッシュによって 1952 年に与えられています。しかしながら Wikipedia によると N = 9 の必勝戦略は数多くの試行にもかかわらず未だ明らかになっていないそうです。N = 100 になったときなど必勝戦略を明らかにする者が現れるとは到底思えません。

（中略）

The moral is that people should distinguish between known (or knowable) polynomial-time algorithms and arbitrary polynomial-time algorithms. People might never be able to implement a polynomial-time-worst-case algorithm for satisfiability, even though P happens to equal NP.

ここから得られる教訓はこうです。すでに知られている（もしくは知ることができる）多項式時間アルゴリズムという概念と、任意の多項式時間アルゴリズムという概念とは、区別しなければならないということです。P は NP と等しいのかもしれませんが、充足可能性問題に対して、最悪計算量が多項式時間となるアルゴリズムを作り上げるようなことは人類にはできないかもしれません。

以上です！お疲れさまでした！

1. Turing machine（チューリングマシン）の略。 ↩

2. HQ9+ など、ジョーク目的で作られたような明らかに非実用的な言語は除きます。 ↩

3. Paul Rendell. Turing Machine Universality of the Game of Life. Springer Cham, 2016. ↩

4. そー(yos1up). マリオメーカーはチューリング完全だった【万能計算機】. 5 February 2017, https://www.nicovideo.jp/watch/sm30573682. ↩

5. Alex Churchill, Stella Biderman, and Austin Herrick. Magic: the Gathering is Turing Complete. 2019. ↩

6. Halting Problem（停止性問題）の略。 ↩

7. Hamiltonian cycle problem（ハミルトン閉路問題）の略。Halting Problem（停止性問題）の H とかぶっちゃた・・・ ↩

8. Verifier（検証機械）の略。 ↩

9. $W$ は Witness（証拠）の略。なので「文字列 $S$ に対する証拠」は $W_S$。 ↩

10. 文字列 $S$ に対し、$|S|$ で「$S$ の長さ」という意味になります。例えば $S$ が "abc" ならば $|S| = 3$ です。 ↩

11. 手前みそになりますが、RSA 暗号の詳細についてはこちらからどうぞ。 ↩

12. Manindra Agrawal, Neeraj Kayal, and Nitin Saxena. PRIMES Is in P. Annals of Mathematics, Vol. 160, No. 2, p. 781–793, 2004. ↩

13. Sualeh Asif, Michael Coulombe, Erik D. Demaine, Martin L. Demaine, Adam Hesterberg, Jayson Lynch, and Mihir Singhal. Tetris is NP-hard even with O(1) Rows or Columns. Journal of Information Processing, Vol. 28, p. 942-958, 2020. ↩

14. 松金輝久 and 武永康彦. 一般化ぷよぷよのNP完全性. 数理解析研究所講究録, No. 1426, p. 147-152, 2005. ↩

15. Greg Aloupis, Erik D. Demaine, Alan Guo, and Giovanni Viglietta. Classic Nintendo games are (computationally) hard. Theor. Comput. Sci., Vol. 586, No. C, p. 135-160, 2015. ↩ ↩² ↩³ ↩⁴ ↩⁵

16. informIT. Twenty Questions for Donald Knuth. 20 May 2014, https://www.informit.com/articles/article.aspx?p=2213858. ↩

17. 対象の存在だけを証明し、具体例は示さない証明のこと。 ↩

18. ボードゲームの一種。 ↩