「0 と 0 の最大公約数はなにか?」という問いに対しては以下の二つの回答が真っ先に挙がるでしょう。
- 0 と 0 の公約数に上限はない。だから 0 と 0 の最大公約数は $\infty$ である。
- いや、$\infty$ は数ではない。だから 0 と 0 の最大公約数は未定義である。
この「無限派」と「未定義派」が大多数を占めると思います。しかしこの記事では、「0 と 0 の最大公約数は 0 である」という主張をご紹介します。
「順序」とはなにか?
「いやいや、"1" だって "2" だって 0 と 0 の公約数なんだから、"0" が最大公約数なわけがないじゃん」とお思いの方もいるでしょう。確かに 1 や 2 は 0 より大きい、つまり言い方を変えれば 1 や 2 は 0 よりも「後ろ」にいます。
しかし最大公約数について論じる場合はとある「特殊な順序」を考えると都合がいいのです。その「特殊な順序」では、0 が 1 や 2 よりも後ろに来るのです。と言われても全然わからないと思うので、そもそも順序とは何ぞや?ということについて考えてみましょう。
二項関係
こんな集合を考えます。
\displaylines{
A = \{\text{太郎}, \text{花子}, \text{伸二}\}\\
B = \{\text{トム}, \text{メグ}, \text{ジョー}\}
}
太郎たち 3 人とトムたち 3 人の組み合わせは集合 $A$ と集合 $B$ の直積 $A \times B$ で以下が考えられます。
\begin{align}
A \times B = \{\\
&(\text{太郎}, \text{トム}), (\text{太郎}, \text{メグ}), (\text{太郎}, \text{ジョー}),\\
&(\text{花子}, \text{トム}), (\text{花子}, \text{メグ}), (\text{花子}, \text{ジョー}),\\
&(\text{伸二}, \text{トム}), (\text{伸二}, \text{メグ}), (\text{伸二}, \text{ジョー})\\
\}
\end{align}
ここで「太郎とジョー」、「花子とトム」はペンフレンドであるとします。つまり、下の集合 $R$ は誰と誰がペンフレンドなのかという「関係」を表していると言えます。
$$ R = \{(\text{太郎}, \text{ジョー}), (\text{花子}, \text{トム})\} $$
そして当然ですが、$R$ は上でお見せした $A \times B$ の部分集合です。このように、二つの集合 $A$, $B$ の直積 $A \times B$ の部分集合 $R$ を $A$, $B$ 上の二項関係といいます。
"R" は "Relation"(関係)の略です。
$A \times B$ の要素 $(a, b)$ が $R$ の要素である、つまり言い方を変えれば「関係 $R$ を満たす」とき、これを $R(a, b)$ とか $_aR_b$ と表記します。
つまり $R(\text{太郎}, \text{ジョー})$ や $_\text{花子} R _\text{トム}$ が成り立つわけです。また、ある関係を表す記号をその場で定めてしまう場合もあります。例えば「記号 "$\simeq$" はペンフレンド関係を表すものとする」とか宣言したうえで $\text{太郎} \simeq \text{ジョー}$ とか書くわけです。
同値関係
与えられた二集合に対し二項関係は好きなように定めることができますが、その中でもあるよい性質を持つものは同値関係と呼ばれます。この同値関係というのは、ざっくり説明すると「同じ」という概念を抽象化したものになります。そこで「『同じ』であるとはいかなることか」を考えてみましょう。「同じ」という二項関係を記号 "$\sim$" で表すと、二項関係 $\sim$ は以下の三つの性質を満たします。
- 反射律:$\forall a [a \sim a]$. すなわち、任意のものは自分自身と「同じ」である。
- 対称律:$\forall a, b [a \sim b \implies b \sim a]$. すなわち、$a$ が $b$ と「同じ」ならば $b$ も $a$ と「同じ」である。
- 推移律:$\forall a, b, c [a \sim b \land b \sim c \implies a \sim c]$. すなわち、$a$ が $b$ と「同じ」で $b$ が $c$ と「同じ」ならば $a$ も $c$ と「同じ」である。
最も一般的な意味での「等しい」という関係、すなわち我々が小学校の算数の時間から使い続けている "=" という関係がこの三つの性質を満たすことは簡単に確認できるでしょう。
・・・いったい何の話がしたいんだ?とお思いの方もいるでしょう。そこで、自然数同士のこんな二項関係 $\equiv$ を考えてみましょう。
$a \equiv b$ とは、$a$ を 3 で割ったあまりと、$b$ を 3 で割ったあまりが等しいことである。
例えば $1 \equiv 1$ や $10 \equiv 10$ が成り立ち、またそれのみならず $2 \equiv 8$ とか $19 \equiv 100$ とかが成り立ちます。つまりこの関係 $\equiv$ は、最も一般的な意味での「等しい」とは異なる関係です。
にもかかわらずこの関係 $\equiv$ は上の 3 性質をすべて満たします。すなわち $\equiv$ は同値関係なのです。つまり、関係 $\equiv$ は抽象的な意味では一種の「同じという関係」なのです。ですからこの関係を使用する文脈においては 2 と 8 は「同じ」ですし、19 と 100 も「同じ」なのです。
ここで私が言いたいのは、何が「同じ」で何が「同じでない」のかは我々自身が勝手に決めてしまっていいということです。数学者カントールは「数学の本質はその自由性にある」と言ったとされますが、まさにこの言葉の通り、「『同じ』とはいかなることか」は自由に決めていいのです。
順序関係
二項関係のうち、また別の「よい性質」を持つものは順序関係と呼ばれます。ここで「$a$ が $b$ 以下である」ことを $a \preceq b$ と表記することにしますが、ここでいう「以下である」とは我々が小学校で習った「最も一般的な意味での『以下』」とは別の概念であることに注意してください。さて関係 $\preceq$ はこんな性質を満たします。
- 反射律:$\forall a [a \preceq a]$. すなわち、任意のものは自分自身「以下」である。
- 推移律:$\forall a, b, c [a \preceq b \land b \preceq c \implies a \preceq c]$. すなわち、$a$ が $b$「以下」で $b$ が $c$「以下」ならば $a$ も $c$「以下」である。
- 反対称律:$\forall a, b [a \preceq b \land b \preceq a \implies a \sim b]$. すなわち、$a$ が $b$「以下」かつ $b$ が $a$「以下」ならば、$a$ と $b$ は所与の同値関係を満たす。
- 全順序律:$\forall a, b [a \preceq b \lor b \preceq a]$. すなわち任意の $a$ と $b$ に対し、$a$ が $b$「以下」と、$b$ が $a$「以下」の少なくとも一方が成り立つ。
いわゆる「小なりイコール」とか「大なりイコール」がこの 4 つの性質全てを満たすことはお判りいただけるでしょう。ですがここではもう少し細かく分類します。
- 反射律と推移律を満たす二項関係を前順序関係と呼ぶ。
- 反対称律を満たす前順序関係を半順序関係と呼ぶ。
- 全順序律を満たす半順序関係を全順序関係と呼ぶ。
「小なりイコール」や「大なりイコール」は 4 つ全ての性質を満たしていたので全順序関係です(それと同時に前順序関係と半順序関係でもあります)。自然数は 0, 1, 2, ... と無限に一列に並んでいるわけですが、全順序関係はこのように「一列にきれいに並んでいる順序」を表します。
その一方で、(全順序関係でない)前順序関係や半順序関係は一列にきれいに並びません。実際、全順序律が成り立たないわけですから、$a \preceq b$ も $b \preceq a$ も成り立たないケースが存在します。つまりこういう場合 $a$ と $b$ のどちらが小さいともどちらが大きいとも言えません。これを「比較不能」といいます。今はあくまでも通常の意味より一段階抽象化した順序関係について論じているので、比較不能の存在もとりあえず許容してしまうわけですね。
整除関係
ここで自然数の整除関係について考えます。
$a \mid b$ とは、自然数 $a$ が自然数 $b$ の約数であることである。
この関係はどのような性質を満たすでしょうか。
まず反射律は満たされます。任意の数 $x$ は $x = 1 \times x$ より自分自身の約数だからです。
また推移律も満たされます。$a$ が $b$ の約数であるなら $b = ax$ を満たす $x$ が存在し、$b$ が $c$ の約数であるなら $c = by$ を満たす $y$ が存在し、したがって $c = a(xy)$ が成り立つことから $a$ は $c$ の約数だからです。
そして反対称律も満たされます。$a$ が $b$ の約数であるなら $b = ax$ を満たす $x$ が存在し、$b$ が $a$ の約数であるなら $a = by$ を満たす $y$ が存在し、したがって $a = a(xy)$ が成り立ちますが、$x$ と $y$ は自然数なのでこの解は $x = y = 1$ しか存在しません。よって $a = b$ が導かれます。
この一方で全順序律は成り立ちません。8 と 10 などはどちらも他方の約数ではないからです。
以上より、整除関係は半順序関係です。約数と順序なんて全く関係なさそうなのに、整除関係は抽象的な意味で順序であると言えるのです。
ハッセ図
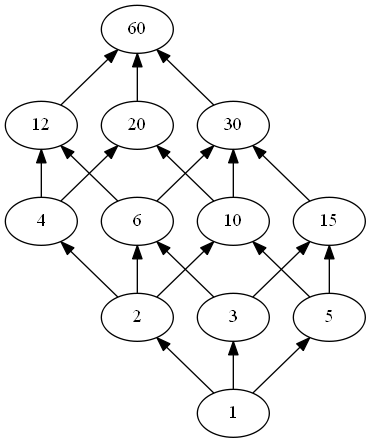
整除関係は半順序関係でしたが、この半順序関係を視覚的にわかりやすく表現できるハッセ図という方法があります。例として「60 の約数の整除関係」(これも半順序関係です)をハッセ図で表現します。
矢印で結ばれた要素同士は半順序関係を満たします。さらに推移律により、いくつかの矢印をたどってたどり着ける要素同士も半順序関係を満たします。例えば "5" からは何本かの矢印をたどって "30" に到達できるので、5 は 30 の約数であると言えます。一方で "3" から "20" へはたどり着けないので、3 と 20 は比較不能です。
またこの図から最大公約数を求めることもできます。ある頂点よりも下位に並んでいる頂点群を「子孫」と呼ぶことにすると、二つの数の一番近い共通子孫が最大公約数になります。例えば 20 と 15 の一番近い共通子孫は 5 なので、ここから 20 と 15 の最大公約数が 5 と求まることがわかります。
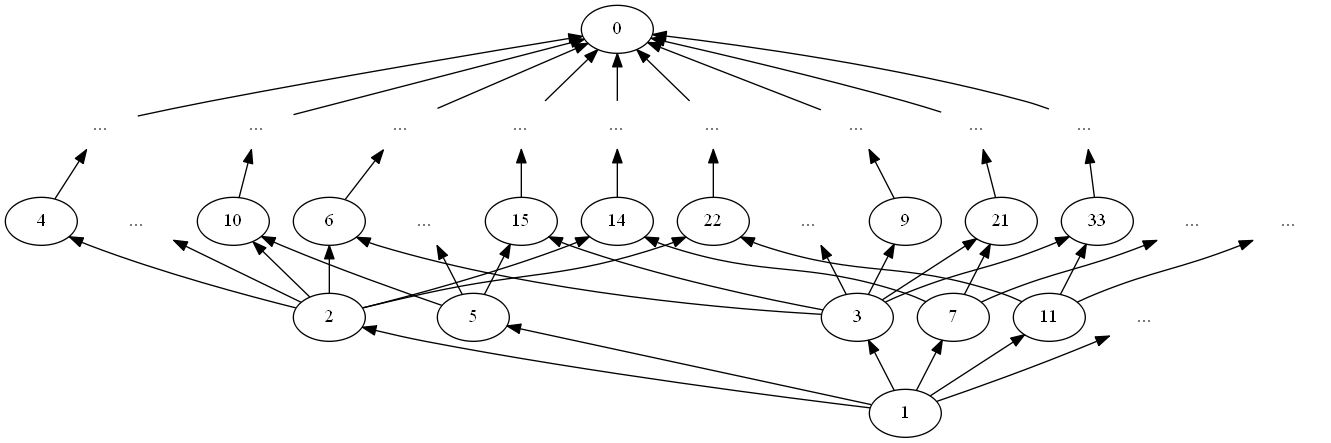
さて今はハッセ図の説明のために「60 の約数」に限定してお話ししましたが、全自然数の整除関係のハッセ図も作ってみましょう。ちょっと見づらいですがこのようになります。
このハッセ図でも先ほどと同様、共通子孫を観察することで最大公約数が求められます。ただし念のため、「一番近い共通子孫」が必ず一意に定まることは証明しておきましょう。
(証明)
まずどんな数も "1" を共通子孫に持ちます。したがって任意の二数は少なくとも一つの共通子孫を持ちます。これで共通子孫の存在性は示せたので、次に一意性を示します。
ある数 $x$ と $y$ が 同じ近さの異なる共通子孫 $a$ と $b$ を持つと仮定します。ここで $a$ と $b$ にはとある共通点があります。
上のハッセ図において、一番下には "1" がいます。そしてその一段上には 2, 3, 5, 7, 11, ... といった素数が並んでいます。そしてその上には $4 (= 2 \times 2)$ や $15 (= 3 \times 5)$ など、二つの素数の積で表せる数が並びます。以下同様、このハッセ図において下から $N$ 段目には「重複込みで $N$ 個の素因数を持つ自然数」が並びます。つまり $a$ と $b$ は重複込みで同じ数の素因数を持つことになります。
ここで $a$ と $b$ の素因数のうち最大のものを $P$ とおくと、適当な指数を使って $a = 2^{e_1} \times 3^{e_2} \times \cdots \times P^{e_n}$, $b = 2^{e'_1} \times 3^{e'_2} \times \cdots \times P^{e'_n}$ と表現できます。また $a$ と $b$ はどちらも $x$ と $y$ の公約数なので、ここから $2^{\max(e_1, e'_1)} \times 3^{\max(e_2, e'_2)} \times \cdots \times P^{\max(e_n, e'_n)}$ も $x$ と $y$ の公約数です。これを $c$ と置きます。
仮定より $a \neq b$ だったので、指数の組「$e_1$ と $e'_1$」、「$e_2$ と $e'_2$」、・・・「$e_n$ と $e'_n$」のうち少なくとも一つは異なっているものがあります。したがって $c$ は重複込みで $a$ や $b$ よりも多くの素因数を持つので、$a$ と $b$ よりも上の段に存在しています。しかしこれは $a$ および $b$ が $x$ と $y$ の最も近い共通子孫であったという仮定に矛盾します。したがって、最も近い共通子孫は背理的に一つしか存在しません。
(証明終)
また注目すべきなのは、このハッセ図においては "0" が頂点に君臨しているということです。つまり整除関係という半順序関係においては 0 が最大値なのです。したがって 0 と 0 の最大公約数は 0 である、ということになるのです。
メリット
0 と 0 の最大公約数を 0 と定めることのメリットに、ユークリッドの互除法の記述が簡単になるというものがあります。ユークリッドの互除法はこんなのでした。
\mathrm{gcd}(a, b) = \left\{
\begin{array}{ll}
a & (b = 0) \\
\mathrm{gcd}(b, a \bmod b) & (b \neq 0)
\end{array}
\right.
この定義だと $\mathrm{gcd}(0, 0) = 0$ となりますが、0 と 0 の最大公約数を 0 と定めるのであれば余計な場合分けを追加しなくてよくなります。このような点から見ても、0 と 0 の最大公約数を 0 とする主張はなかなか筋の通ったものなのではないかと思います。
おわりに
ひとつだけ誤解のなきよう明記しておきますが、「0 と 0 の最大公約数は何であるか?」という問いの答えはそのときの流儀によります。記事冒頭では 0 と 0 の最大公約数を「無限」とする立場や「未定義」とする立場をご紹介しましたが、その立場を採用する方が都合がいいときにはそうするべきです。なので「0 と 0 の最大公約数は 0 というのが唯一絶対の正解であり、ほかは間違いである」と主張するべきではありません。先にも引用したように「数学の本質はその自由性にある」のです。自由にやっていきましょう🗽