AtCoder をやるときはスタックサイズを調整しとけ

きっかけ

先日、皆さんご存じ AtCoder でこんな問題が出題されました。

問題の内容は長くなるので省略しますが、再帰関数を使って解ける問題です。ちなみに私が書いたのはこの解説と同じものでした。

#include "atcoder/modint.hpp"
#include <iostream>

using mod_int = atcoder::modint998244353;

mod_int solve(int n, int m)
{
    return n == 1 ? 0 : m * mod_int{m - 1}.pow(n - 1) - solve(n - 1, m);
}

int main()
{
    int n, m;
    std::cin >> n >> m;
    std::cout << solve(n, m).val() << std::endl;
}

理屈には完璧な自信がありました。しかし一部のテストケースでエラーが発生してしまいます。

$ ./a.out
987654 456789
Segmentation fault

このプログラムは全部で n 回の再帰を行うので、n が大きすぎるとスタックを使い果たしてしまうようです。しかし諦めが悪い私はヤケクソになって提出しました。

何が起こった？

AtCoder 内部で使用されているコンパイラオプションは以下で公開されています。

なので、私は「このオプションをコピペしておけば AtCoder 内部と全く同じ環境でプログラムを動かせる」と思い込んでいました。しかしそれは大きな誤りでした。

AtCoder 環境はスタックサイズがわりとデカい

先ほど私の環境で Segmentation fault を起こしたプログラムですが、ｾｸﾞﾌｫの原因がスタック不足であるならばスタックを増やしてやればきちんと動くはずです。まずは現時点でのスタックサイズの確認です。

$ ulimit -s
8192

8192 キロバイトでした。

一方の AtCoder はどうでしょうか。AtCoder は Bash にも対応しているため、コードテストページから ulimit -s を実行することでスタックサイズを知ることができます。


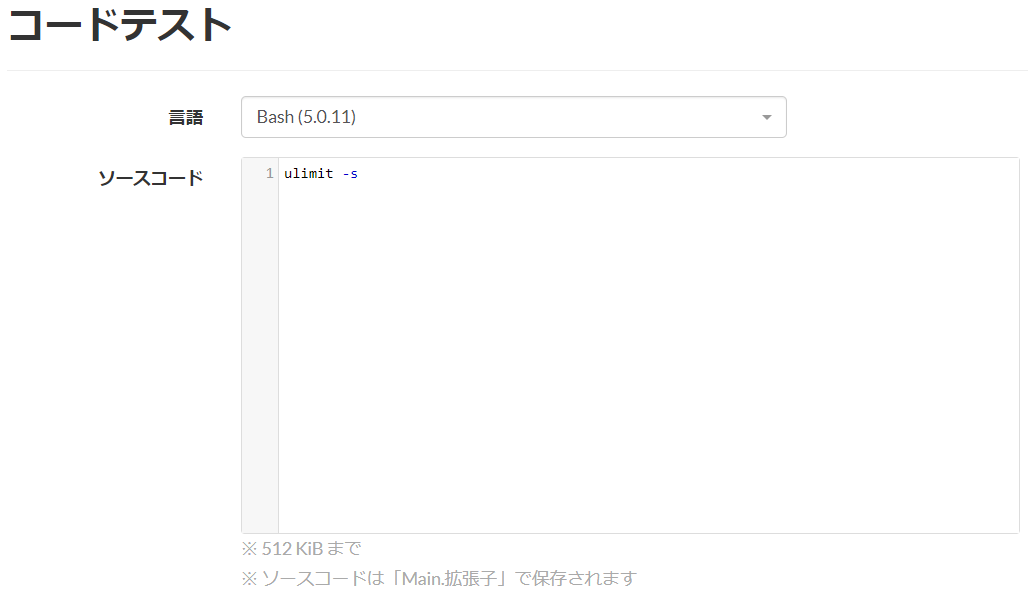
1048576 キロバイト。私の環境の実に 128 倍です。

ところでさっき私が解こうとしていた問題のメモリ制限のところを見てみましょう。

メモリ制限の 1024 メガバイトとは、すなわち 1048576 キロバイトです。最初からここに書いてあったんですね。

「え？1024 メガバイトと 1048576 キロバイトってだいぶ違くない？」とお思いの方もいるかもしれません。ここには「キロバイト」や「メガバイト」などをめぐるややこしい事情が存在します。

そもそも「キロ」や「メガ」は SI 接頭辞といい、それぞれ「1000 倍」や「1000000 倍」を意味する言葉です。さらに 1000000000 倍なら「ギガ」、1000000000000 倍なら「テラ」と続きます。

ところがデータ容量を表す場合に限って厄介な俗習が存在するのです。プログラマーという特殊な生き物は「十進法より二進法を好む」という特殊な嗜好を持ちますので、あるときから「キロ」が勝手に 1024 倍 という意味で使われ出してしまったのです。これと同じ調子で「メガ」は 1048576 倍、「ギガ」は 1073741824 倍……と、2 の冪に合わせる用法が広がってしまいました。こういうわけで、「1 キロバイト」と言った場合「1000 バイト」を指す場合と「1024 バイト」を指す場合の二つが存在することになってしまったのです。

この混乱を避けるため、2 の冪を基準とするデータ容量は二進接頭辞で表すという流儀も存在します。即ち 1024 バイトは 1 キビバイト (KiB)、1048576 バイトは 1 メビバイト (MiB) …… という具合です。ですが残念ながらこちらはあまり普及しているとは言えません。

話を戻しますと、今回の問題におけるメモリ制限は正確には「1024 メビバイト」だったということであり、これは先ほど ulimit -s で見たスタックサイズ「1048576 キビバイト」と厳密に一致します。

そういうわけですから、手元の環境でもスタックサイズを変更して試してみましょう。

$ ulimit -S -s 1048576
$ ./a.out
987654 456789
778634319

無事にちゃんと動きました。

ほかの解決策

1. 末尾再帰最適化が効くようにする

末尾再帰最適化が効くようなコードを書くことで、定数容量のメモリで任意回の再帰が行えるようになります。詳しい解説はこちらの記事をご覧ください。今回の問題に強引に末尾再帰を適用するとこのようなコードになります。

#include "atcoder/modint.hpp"
#include <iostream>

using mod_int = atcoder::modint998244353;

int n, m;

mod_int tail_recursive_func(int _n, mod_int acc)
{
    return _n > n ? acc : tail_recursive_func(_n + 1, m * mod_int{m - 1}.pow(_n - 1) - acc);
}

int main()
{
    std::cin >> n >> m;
    std::cout << tail_recursive_func(2, 0).val() << std::endl;
}

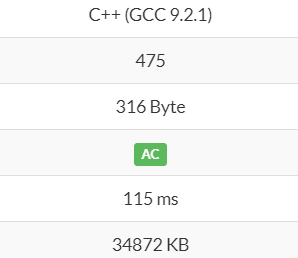
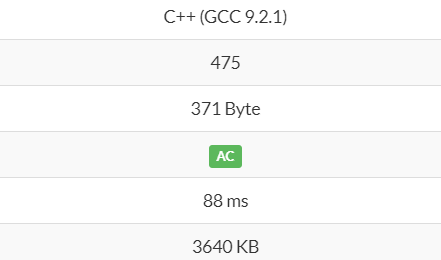
このように、実に 10 倍近くメモリを削減できています。

単純な再帰バージョン	末尾再帰バージョン

2. そもそも再帰すんな

一番安全かつ簡単なのはこちらでしょうか。そもそも深すぎる再帰はその分関数呼び出しのオーバーヘッドも増えるので、競技プログラミングでは不利と言わざるを得ません。

#include "atcoder/modint.hpp"
#include <iostream>

using mod_int = atcoder::modint998244353;

int main()
{
    int n, m;
    std::cin >> n >> m;
    mod_int ans = 0;
    for (int i = 2; i <= n; ++i) {
        ans = m * mod_int{m - 1}.pow(i - 1) - ans;
    }
    std::cout << ans.val() << std::endl;
}

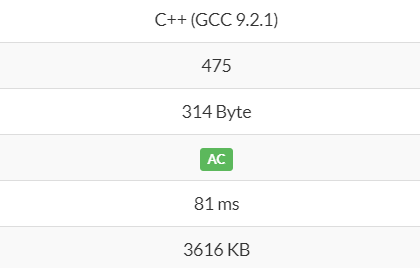
実行時間から見ても消費メモリから見ても末尾再帰バージョンと大差ないようです。再帰回数が絶対に少なくて済むと言い切れるとき以外は再帰しないのが無難っぽいですね。

教訓

諦めたらそこで試合終了ですよ。