TL; DR
はじめに
「2.5 次元」という言葉、最近よく耳にしますよね。アニメなどを原作とするミュージカル作品などを「2 次元と 3 次元の間」ということで「2.5 次元」というわけです。私も観たことあります。面白かったです。
しかしこの「2.5 次元」という表現はなんだかモヤっとします。以上でも以下でもないとかベクトルが違うとか人一倍とかと同じくらいモヤっとします。なのでどうにかして整合性を持たせましょう。
次元とは
まず初めに次元とは何か考えます。たとえば平面が 2 次元であることは皆さんご存知でしょう。この平面上の適当な位置に原点と $x$ 軸、$y$ 軸をとります。すると平面上の任意の点が $x$ 座標、$y$ 座標の組み合わせで表現できるようになります。
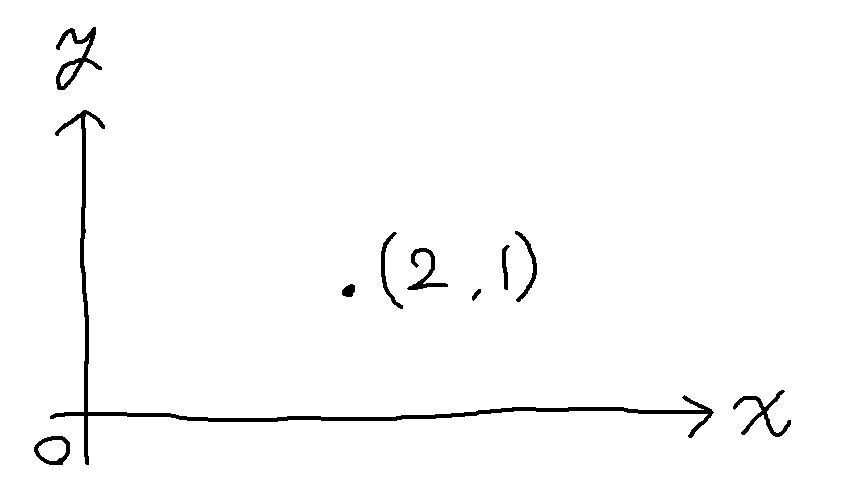
またこの場合はどうでしょう。
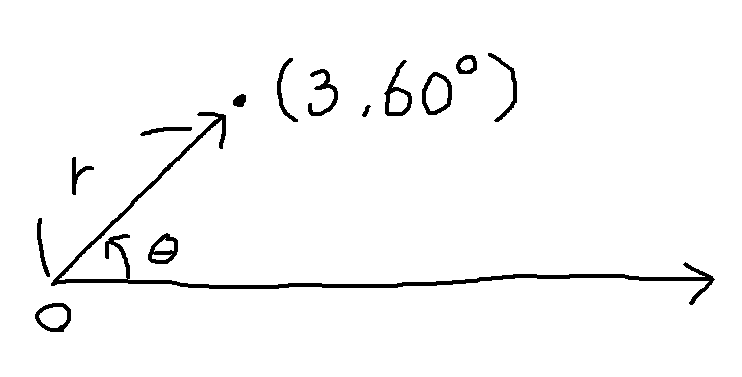
$x$ 座標と $y$ 座標の代わりに、原点からの距離 $r$ と 軸からの角度 $\theta$ をとります。この $r, \theta$ の組み合わせでも平面上の任意の点を表現できます。いわゆる極座標というやつです。
さて平面上の点を指定する二つの方法をお見せしましたが、どちらの方法も二つの変数を必要としていました。つまり「$x$ と $y$」あるいは「$r$ と $\theta$」です。すなわち「次元」とは、点の位置を指定するのに必要な変数の個数という意味なのです。
相似次元
これで次元が定義されましたが、しかしこれでは「2.5 次元」は定義できません。次元とは「変数の個数」だと言っているんですから、非自然数になりうるはずがありません。そこで、次元という概念をもう少し一般化することでどうにかして 2.5 次元を定義します。ここでカギになるのが「縮小」と「敷き詰め」です。
ここに正方形があります。

この正方形を縦横それぞれ $\frac{1}{3}$ に縮小します。
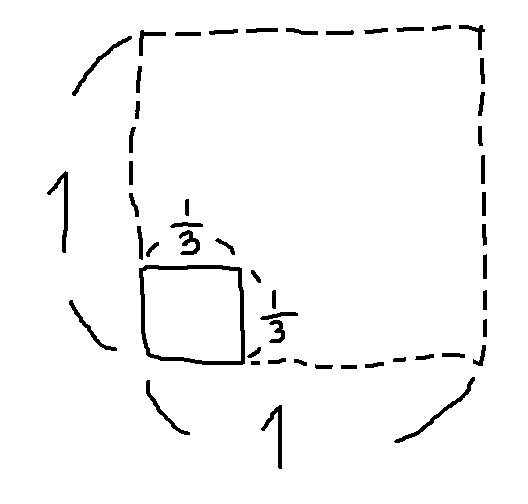
正方形は縦と横のそれぞれで $\frac{1}{3}$ にされたので、面積は $\left(\frac{1}{3}\right)^2=\frac{1}{9}$ になっています。
ここで、この小さくなった正方形で元の正方形を敷き詰めることを考えます。正方形の面積は $\frac{1}{9}$ になっていたので、9 枚敷き詰めればよいです。
より一般に、正整数 $n$ に対し正方形を縦横それぞれで $\frac{1}{n}$ にした場合は $n^2$ 枚敷き詰めればよいです。
次にこの立方体について考えます。
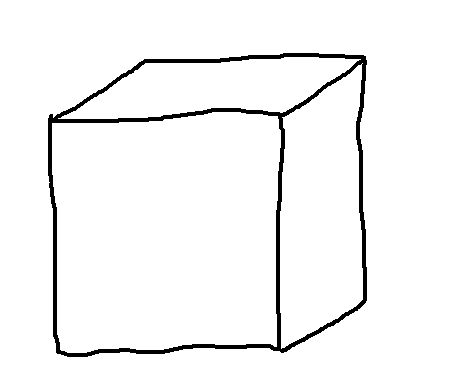
この立方体を縦横奥行きそれぞれ $\frac{1}{3}$ に縮小します。
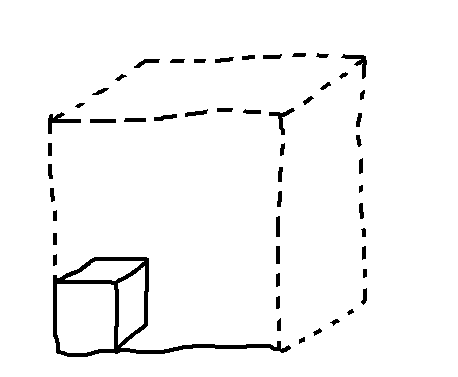
立方体は縦と横と奥行きのそれぞれで $\frac{1}{3}$ にされたので、体積は $\left(\frac{1}{3}\right)^3=\frac{1}{27}$ になっています。
ここで、この小さくなった立方体で元の立方体を敷き詰めることを考えます。立方体の体積は $\frac{1}{27}$ になっていたので、27 個敷き詰めればよいです。
より一般に、正整数 $n$ に対し立方体を縦横奥行きそれぞれで $\frac{1}{n}$ にした場合は $n^3$ 個敷き詰めればよいです。
さて、正方形と立方体の二つのケースを見てきました。この時点で何か法則性が見えてきます。
| 図形 | 各方向に対し $\frac{1}{n}$ に縮小したもので敷き詰めるのに必要な個数 |
|---|---|
| 正方形 | $n^2$ |
| 立方体 | $n^3$ |
ここからの推論により、相似次元という概念を定義します。
ある図形を各方向に対し $\frac{1}{n}$ に縮小したものを $k$ 個敷き詰めて元の図形と同じものを作れるとき、その図形の相似次元は $\log_n{k}$ である。
検算として正方形と立方体の相似次元を計算してみます。正方形の相似次元は $\log_n{n^2}=2$、立方体の相似次元は $\log_n{n^3}=3$ ですから、次元の概念の一般化になっていることがうかがえます。
フラクタル図形
さて正方形と立方体の相似次元は案の定自然数になりましたが、実は数学の世界には相似次元が自然数にならない摩訶不思議な図形が存在します。その代表例がフラクタルです。ここでは一例としてコッホ曲線を取り上げます。
まず始めに適当な長さの線分を用意します。

この線分の $\frac{1}{3}$ の長さの線分を 4 本用意し、それをこのように並べます。
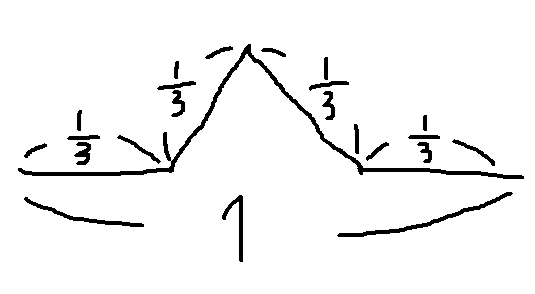
さて、この時点で線分は 4 本存在していますよね?次にこの 4 本の線分それぞれに対しまた同じことをします。つまりこうなります。

この操作の極限として定義されるのがコッホ曲線です。
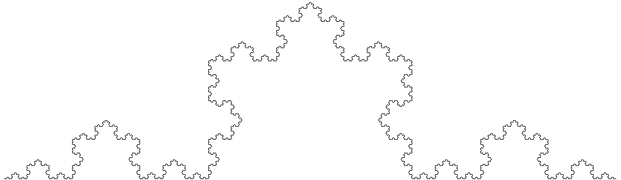 |
|---|
| 「操作」を六回行ったもの |
コッホ曲線は無限回の操作を行った極限として定義されるので、真のコッホ曲線は決して見ることができないことに注意してください。上の図はあくまでもコッホ曲線の近似です。
さてこのコッホ曲線の相似次元について考えます。雑な議論にはなりますが、コッホ曲線は自分自身を $\frac{1}{3}$ に縮小したもの 4 個で敷き詰めを行えます。よってコッホ曲線の相似次元は $\log_3{4}\approx 1.26$ となります。
また、もう少し楽に相似次元を求める方法もあります。先ほどお見せしたコッホ曲線の「作り方」に着目するのです。コッホ曲線は線分から始め、「$\frac{1}{3}$ に縮めたものを 4 個繋げる」ことを繰り返して作ることができました。ここからもコッホ曲線の相似次元が $\log_3{4}$ であることが結論付けられます。つまり、一般に「各方向に $\frac{1}{n}$ に縮めたものを $k$ 個繋げる」ことを繰り返すことで定義されるフラクタルの相似次元は $\log_n{k}$ になるのです。
「いや、無限回の操作を行ったところで線は線なんだからコッホ曲線だって 1 次元だろ」と、納得がいかない方もいるかもしれません。実際「位相次元」という考え方では 1 次元になるそうです。しかし、コッホ曲線はただの曲線にはない特徴を持っています。
まず、コッホ曲線の「ステップ 1」ともいうべきこの図形が収まる領域を考えます。
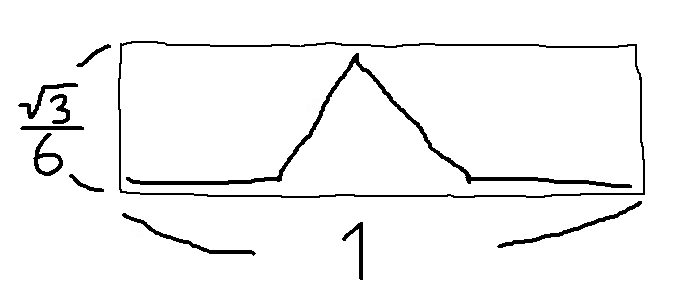
最初に用意した線分の長さを 1 とすると領域の高さは $\frac{\sqrt{3}}{6}$ です。そしてこれは以降変化することはありません。「操作」を何度繰り返してもコッホ曲線は $1 \times \frac{\sqrt{3}}{6}$ の領域に収まります(たぶん)。つまり何が言いたいのかというと、コッホ曲線は有限の領域に存在する曲線だということです。
にもかかわらずコッホ曲線は無限の長さを持ちます。なぜなら「操作」を一回行うごとに長さは $\frac{4}{3}$ 倍になるからです。コッホ曲線の相似次元 $\log_3{4}\approx 1.26$ というのは、まさに「1 次元と 2 次元のはざま」ということを表しているのです。
本題
さてここまでくれば「2.5 次元」のフラクタルを自作することが可能となります。いろいろこねくり回すと $\log_4{32}=2.5$ だと分かるので、「2.5 次元」は「適当な図形を各方向に対し $\frac{1}{4}$ に縮めたものを 32 個敷き詰める」ことを無限に繰り返すことで作れることになります。そこでまずは立方体を用意します(今回はMagicaVoxelを使いました)。

これを各方向に対し $\frac{1}{4}$ に縮めるとこうなります。

次にこれを 32 個敷き詰めます。敷き詰め方は何でもいいのですが、今回はこのように敷き詰めることにします。

あとはこれを永遠に繰り返します。といっても本当に永遠に繰り返すことはできないので、今回は 4 回で打ち止めにしました。それがこちらです。

「操作」を永遠に繰り返すことで体積は 0 に収束し、表面積は発散します。まさに 2 次元と 3 次元のはざまに存在する者といえるでしょう。
ギャラリー
 |
|---|
| 正面(透視投影) |
 |
|---|
| 斜め(正投影) |
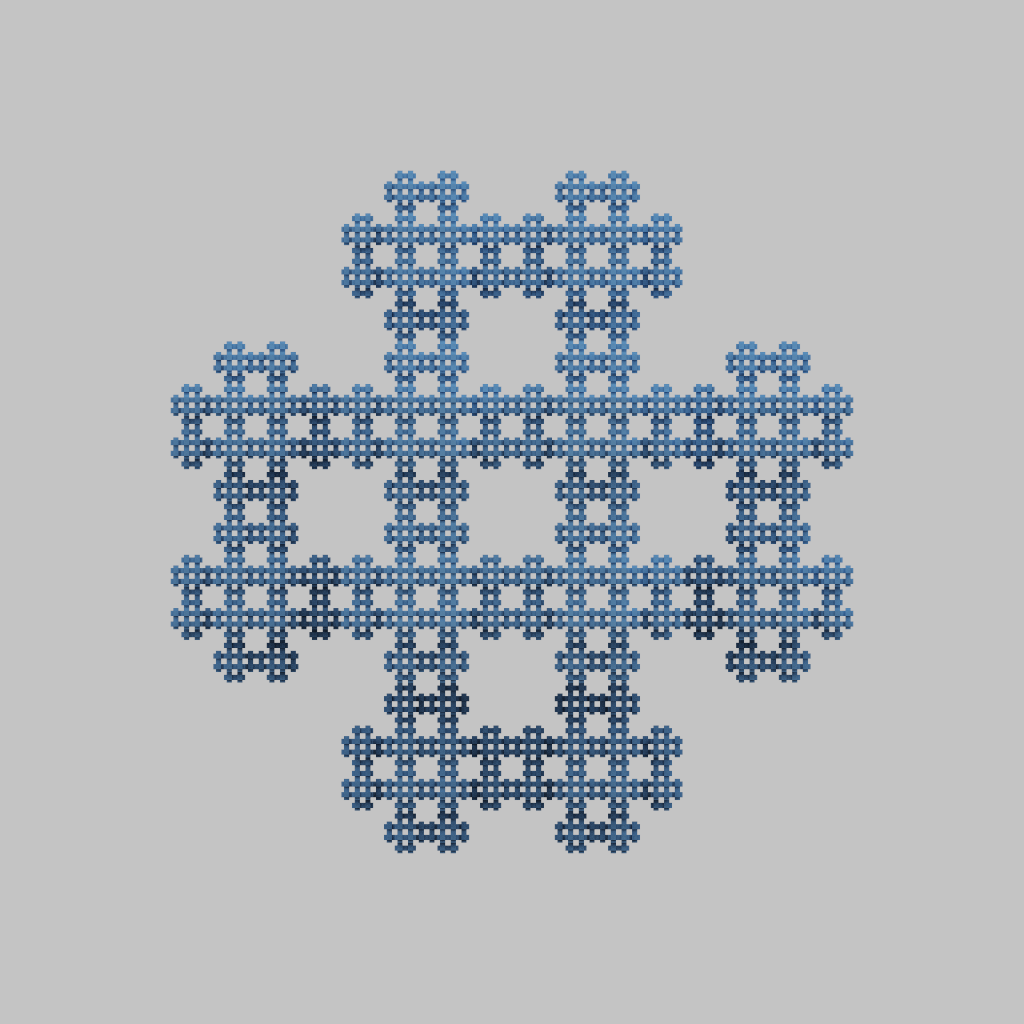 |
|---|
| 正面(正投影) |
 |
|---|
| 内部(透視投影) |
 |
|---|
| 各ステップ(透視投影) |
まとめ
二次元に行きたい人生だった。