おはようございます。
突然ですが「計算量オーダー」ってありますよね。ソートアルゴリズムの計算量が$O(n\log n)$とかいうあれです。
競技プログラミングなんかでは重要になってくる概念なんですが、きっちり説明しろと言われるとなかなか難しいものがあります。というわけでこの「計算量オーダー」をきちんと理解し、明日から人に自慢できるようにしていきましょう。
ランダウの記号
まずは形式的定義から
計算量オーダーの記号としてよくみかけるこれ→$O$ですが、正式名称を「ランダウの記号」といいます。その形式的定義は以下のようになります。
関数$f(x)$, $g(x)$に対し
\exists x_0, \exists M > 0, \forall x > x_0 [|f(x)| \leq M|g(x)|]
を「$f(x)$が($x \rightarrow \infty$において)$g(x)$のオーダーである」といい、$f(x) \in O(g(x))$と表記する。
は?(半ギレ)
落ち着こう
いったん落ち着きましょう。ここからさき話が煩雑になるのを避けるため、当面の間$f(x)$と$g(x)$は正の値のみを取る関数とします。なので絶対値記号も外しちゃって、
\exists x_0, \exists M > 0, \forall x > x_0 [f(x) \leq Mg(x)]
について考えます。これをむりくり日本語で言い表すとこうなります。
とある$x_0$および正の$M$が存在し、$x_0$より大きな任意の$x$に対し$f(x) \leq Mg(x)$が成り立つ。
関数をつよくする
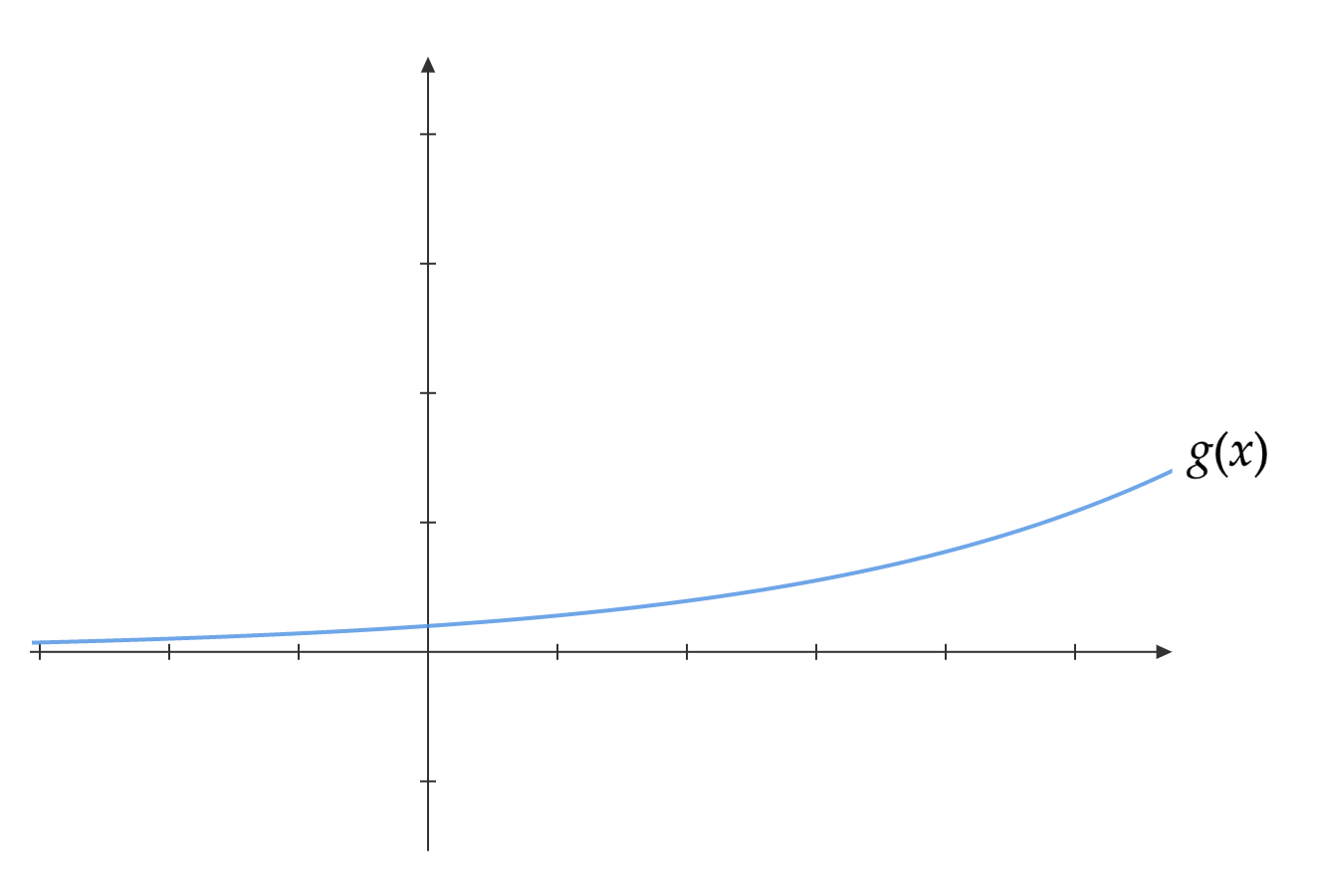
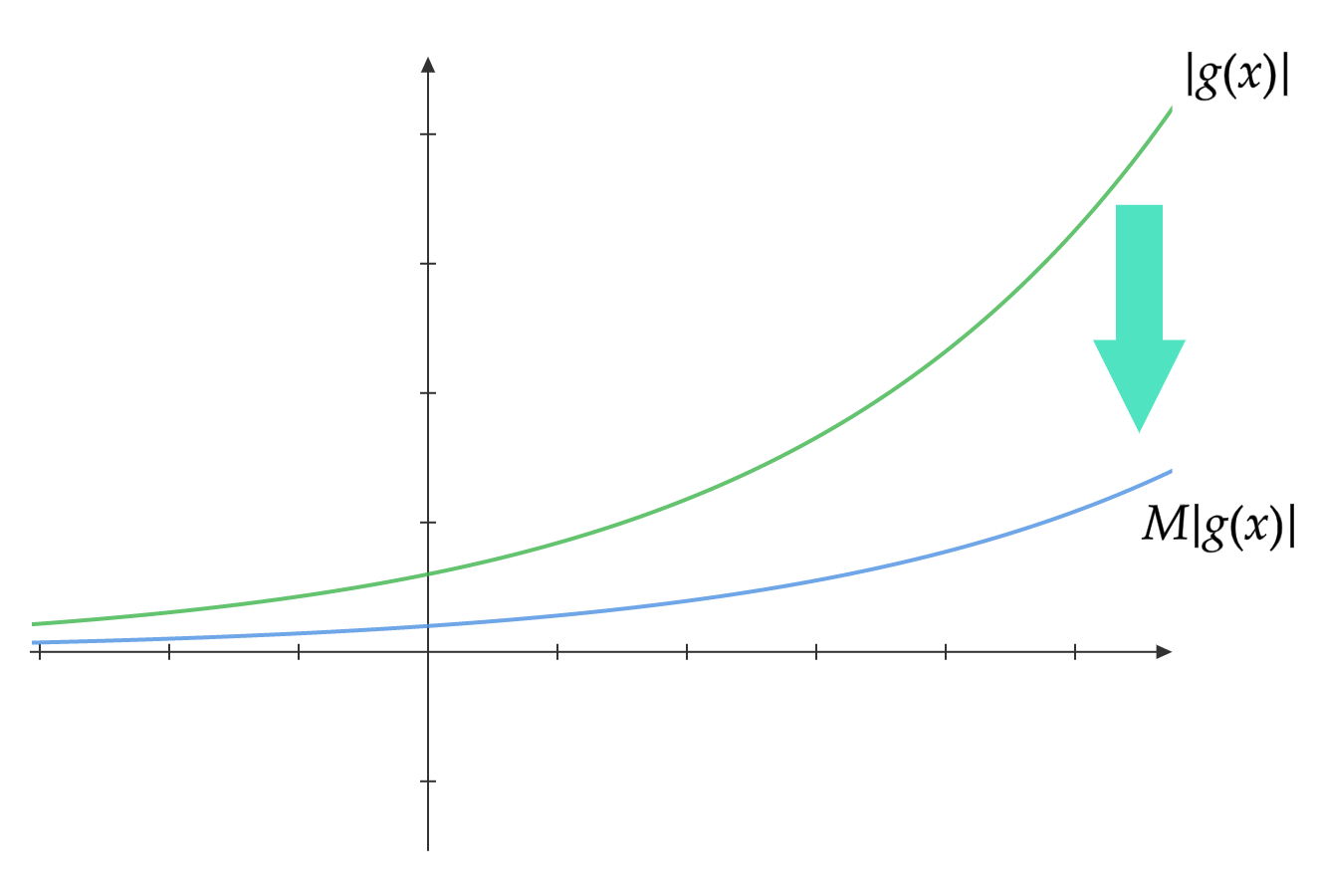
まず注目していただきたいのが$Mg(x)$という部分です。とりあえず仮に$g(x)$がこんな感じの関数であるとします。
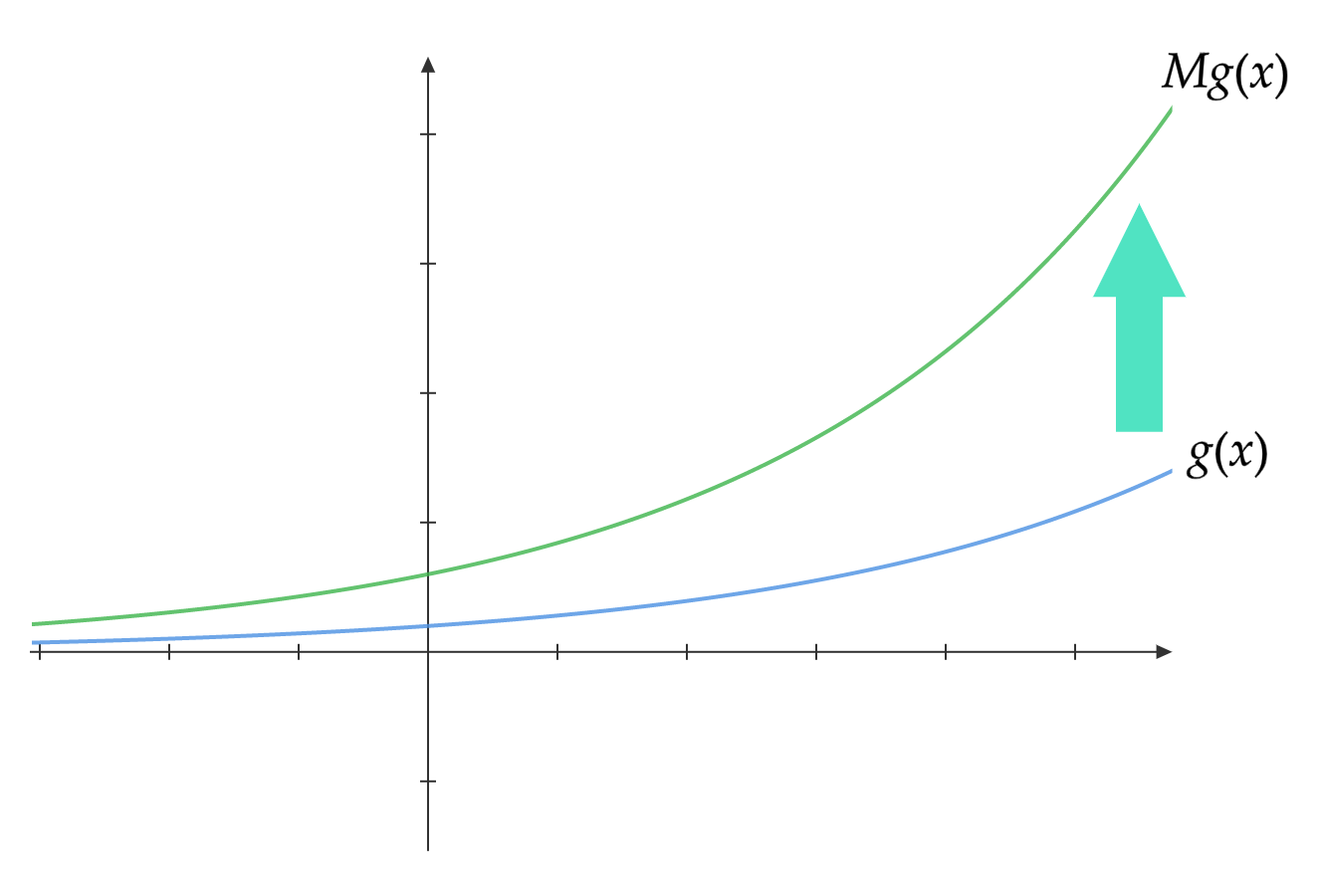
こいつに1より大きい適当な数$M$を掛けてやります。するとこんな風に、全体的にグググっと持ち上がった感じになります。
これを$g(x)$をつよくすると呼ぶことにしましょう。
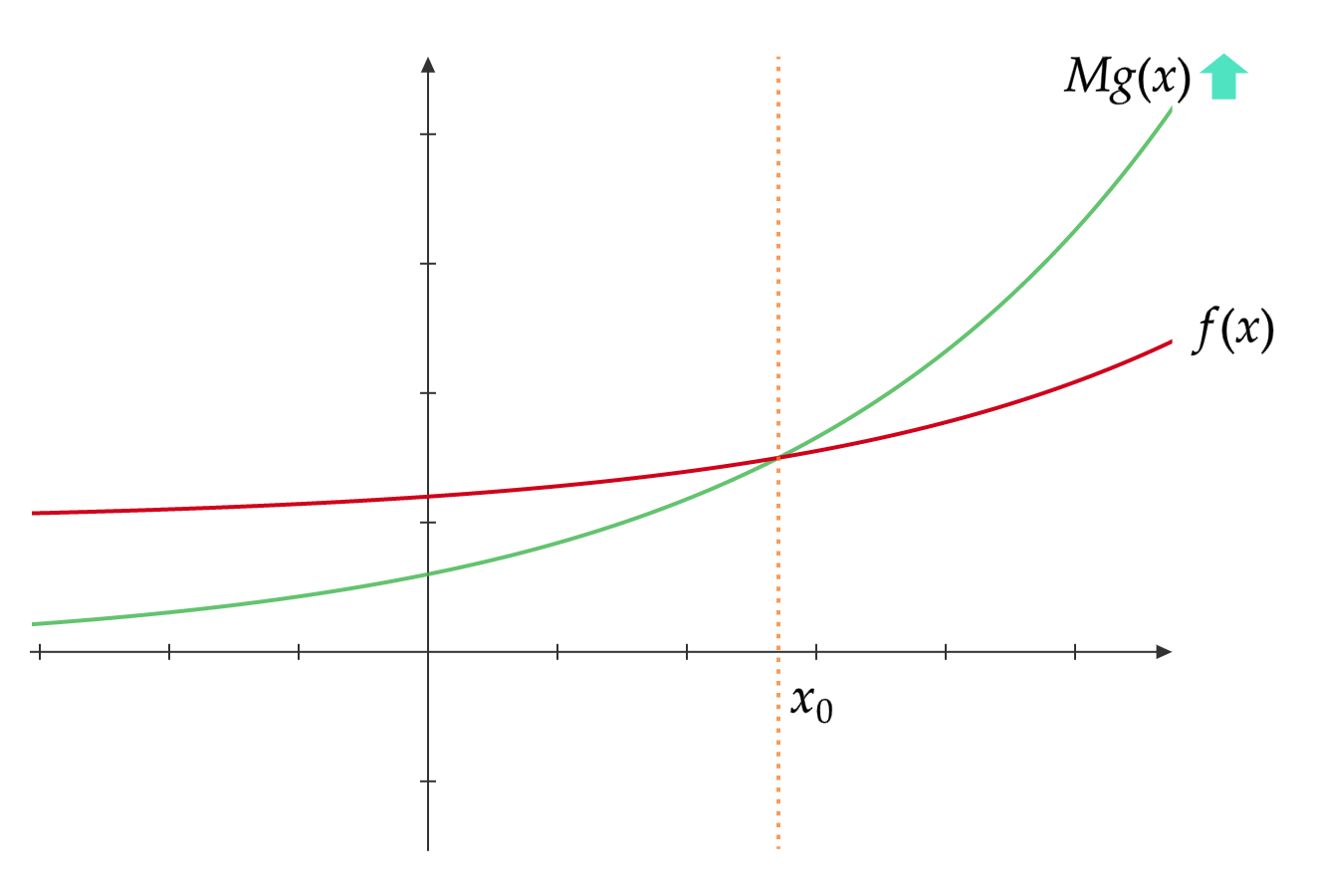
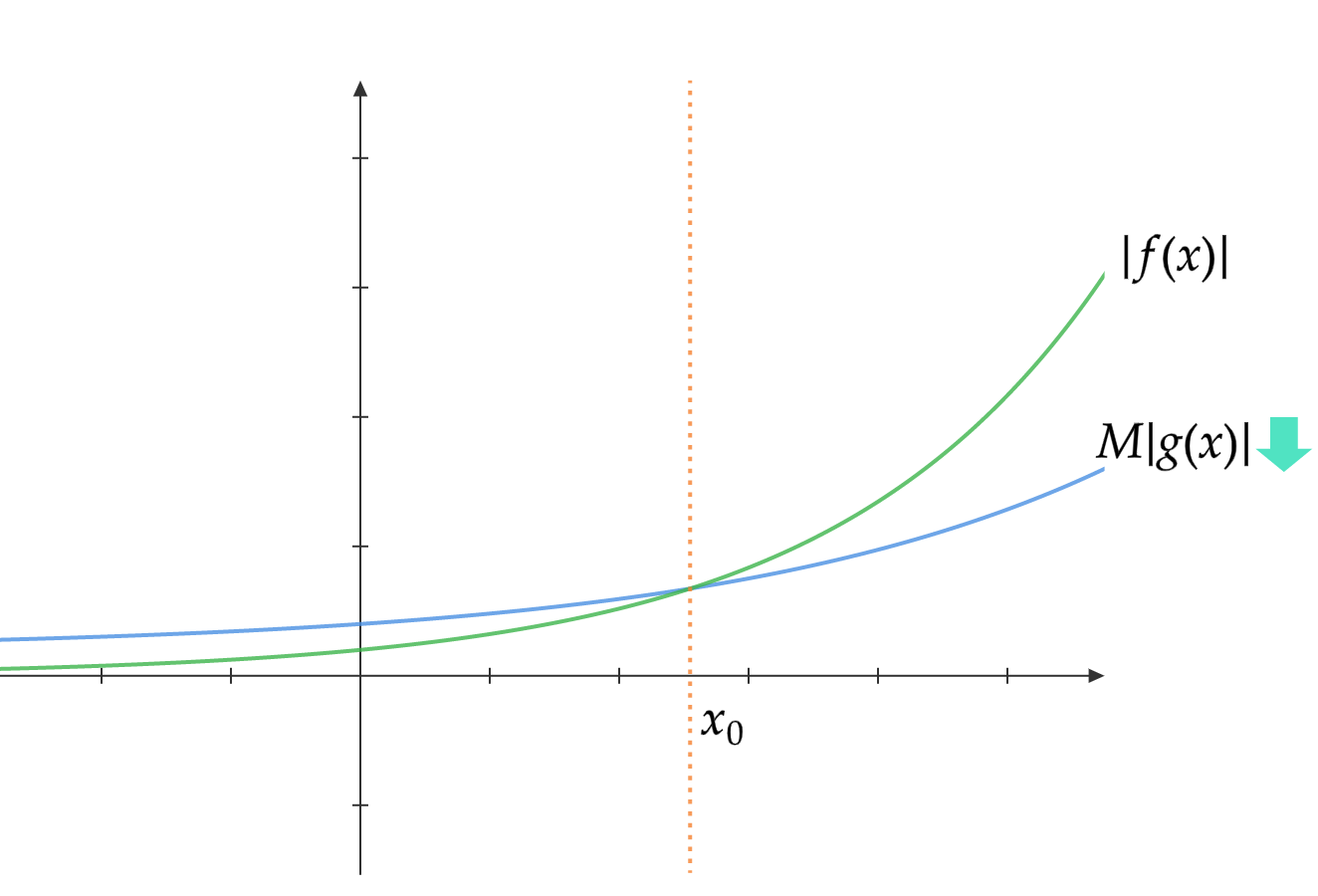
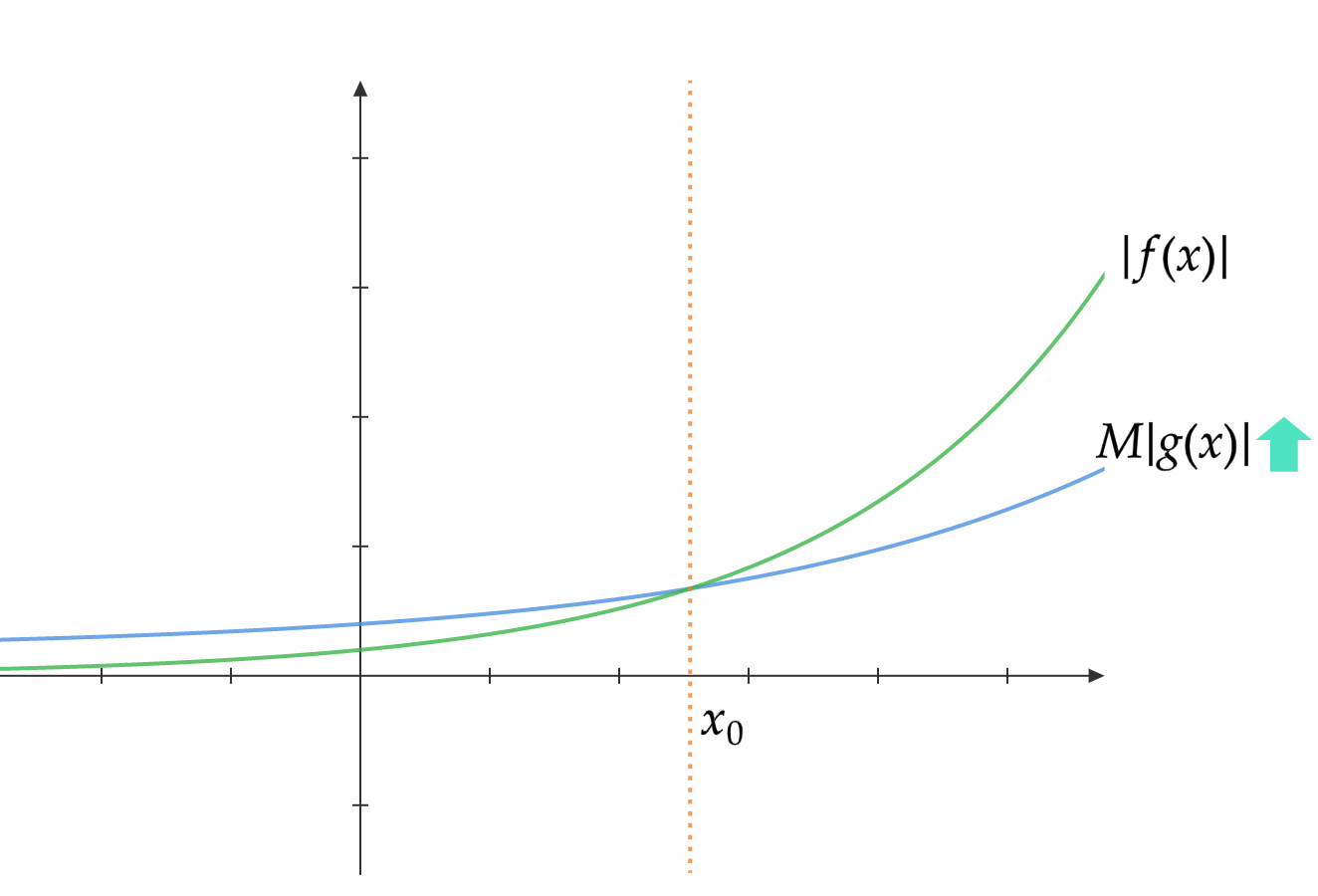
ここでもう一度さきほどのステートメントを見ていきます。
とある$x_0$および正の$M$が存在し、$x_0$より大きな任意の$x$に対し$f(x) \leq Mg(x)$が成り立つ。
これを図示するとこうなります。
$x_0$を境にして、$g(x)$がつよくなった$Mg(x)$が$f(x)$を上回り続けているのがわかると思います。
これがランダウの記号の正体です。つまり$f(x)\in O(g(x))$とは、$g(x)$を適当なだけつよくしてやれば、そのうち$f(x)$をずっと上回り続けるようになる、ということを表しているのです。
補足
さっき取った絶対値記号について
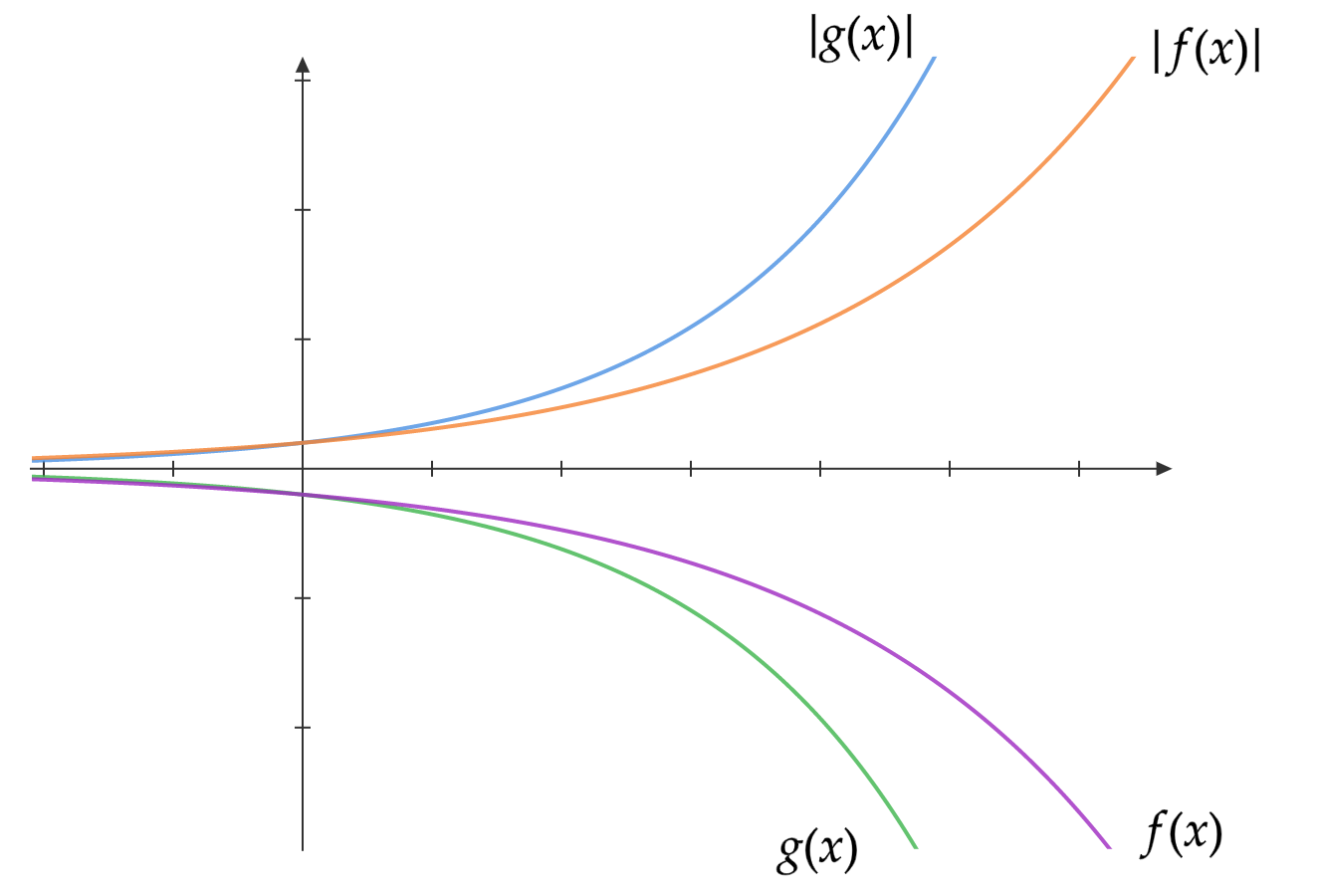
さっきは$f(x)$も$g(x)$も正の値しかとらないとして、勝手に絶対値記号を取ってしまいました。本来の定義はこうなります。
\exists x_0, \exists M > 0, \forall x > x_0 [|f(x)| \leq M|g(x)|]
$f(x)$と$g(x)$は絶対値をとられるので、$f(x)$と$g(x)$が負の値をとるような関数だったとしても結局はこうなります。
つまり関数のオーダーを考えるときは、めっちゃ速く増える関数もめっちゃ速く減る関数も区別はしないことになります。重要なのは変化の程度であって、増えていくのか減っていくのかは本質的なことではないということです。
記法について
$f(x)$が$g(x)$のオーダーであることを$f(x) \in O(g(x))$と表記すると書きましたが、これを$f(x) = O(g(x))$と表記する場合もあります(むしろそっちのほうが一般的かも)。ですがこの記法はいろいろと混乱を招きます。一番わかりやすいのはこのパターンでしょう。
$O(x) = O(x^2)$であるが、$O(x^2) = O(x)$ではない。
これはどういうことかというと、$O(f(x)) = O(g(x))$と書かれているとき、左辺に書かれている方は$f(x)$のオーダーである任意の関数を表しています。そして右辺に書かれている方は$g(x)$のオーダーであるとある関数を表しています。
$x$のオーダーである任意の関数は$x^2$(あるいは$x^2$のオーダーの適当な関数)1を適当につよくすることで上から押さえつけられるので、$O(x)=O(x^2)$は成り立ちます。一方$x^2$のオーダーである関数の一部2は$x$のオーダーである関数をどんなにつよくしても押さえつけることはできないので、$O(x^2) = O(x)$は成り立ちません。
$f(x) \in O(g(x))$のほかに$f(x) \leq O(g(x))$と書く場合もあります。どちらにせよ等号よりは誤解の余地がなくて良いでしょう。
よくある誤解について
$f(x)$が$g(x)$のオーダーであることをこのように説明している文章をよく見かけます。
$f(x)$がおおよそ$g(x)$に比例することを$f(x)=O(g(x))$と書く。
ですがこれは誤りです。上の説明からもわかるように、$g(x)$は適当につよくなることで$f(x)$を押さえつけることさえできればいいので、$g(x)$は$f(x)$をぶっちぎって増加していくようなクソデカ関数であっても構いません。極端な話、バブルソートの計算量は$O((((((({n!}^{{n!}^{{n!}^{n!}}}!)!)!)! \times n^{(99999999^{99999999!}!)!})!)!)!)$であると書いても、間違いではありません。
さてランダウの記号についてはお解りいただけたと思いますが、実は他にも似たような記号が4種類あります。では一つずつ順番に見ていきましょう。
ビッグ・オメガ
形式的定義は以下のようになります。
$f(x) \in \Omega(g(x))$とは、
\exists x_0, \exists M > 0, \forall x > x_0 [|f(x)| \geq M|g(x)|]
が成り立つことである。
関数をよわくする
今度はさっきとは逆に関数をよわくすることを考えます。ここで$|g(x)|$に対して1より小さい適当な正の数$M$を掛けてやれば、このように$|g(x)|$はグググっと押しつぶされたような形になります。
$f(x) \in \Omega(g(x))$を図示するとこのようになります。
つまり$f(x) \in \Omega(g(x))$とは、$g(x)$を適当によわくすることで$f(x)$を下から抑えられることを意味します。
ビッグ・シータ
形式的定義は以下のようになります。
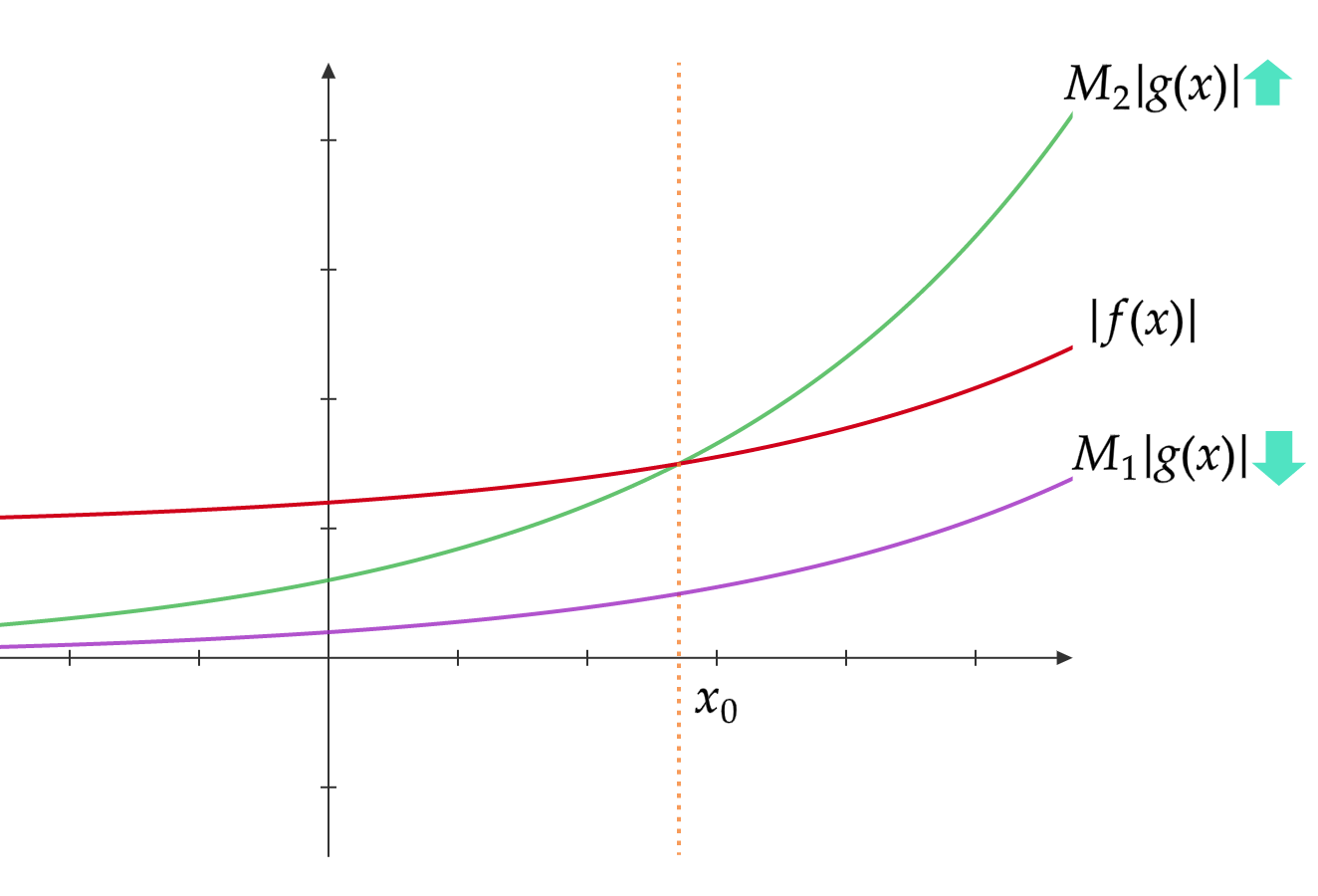
$f(x) \in \Theta(g(x))$とは、
\exists x_0, \exists M_1 > 0, \exists M_2 > 0, \forall x > x_0 [M_1|g(x)| \leq |f(x)| \leq M_2|g(x)|]
が成り立つことである。
式からもわかるようにこれは$O(g(x))$と$\Omega(g(x))$の合わせ技です。つまり$g(x)$を適当につよくすれば$f(x)$を上から抑えられ、適当によわくすれば$f(x)$を下から抑えられることを意味します。
スモール・オミクロン
形式的定義は以下のようになります。
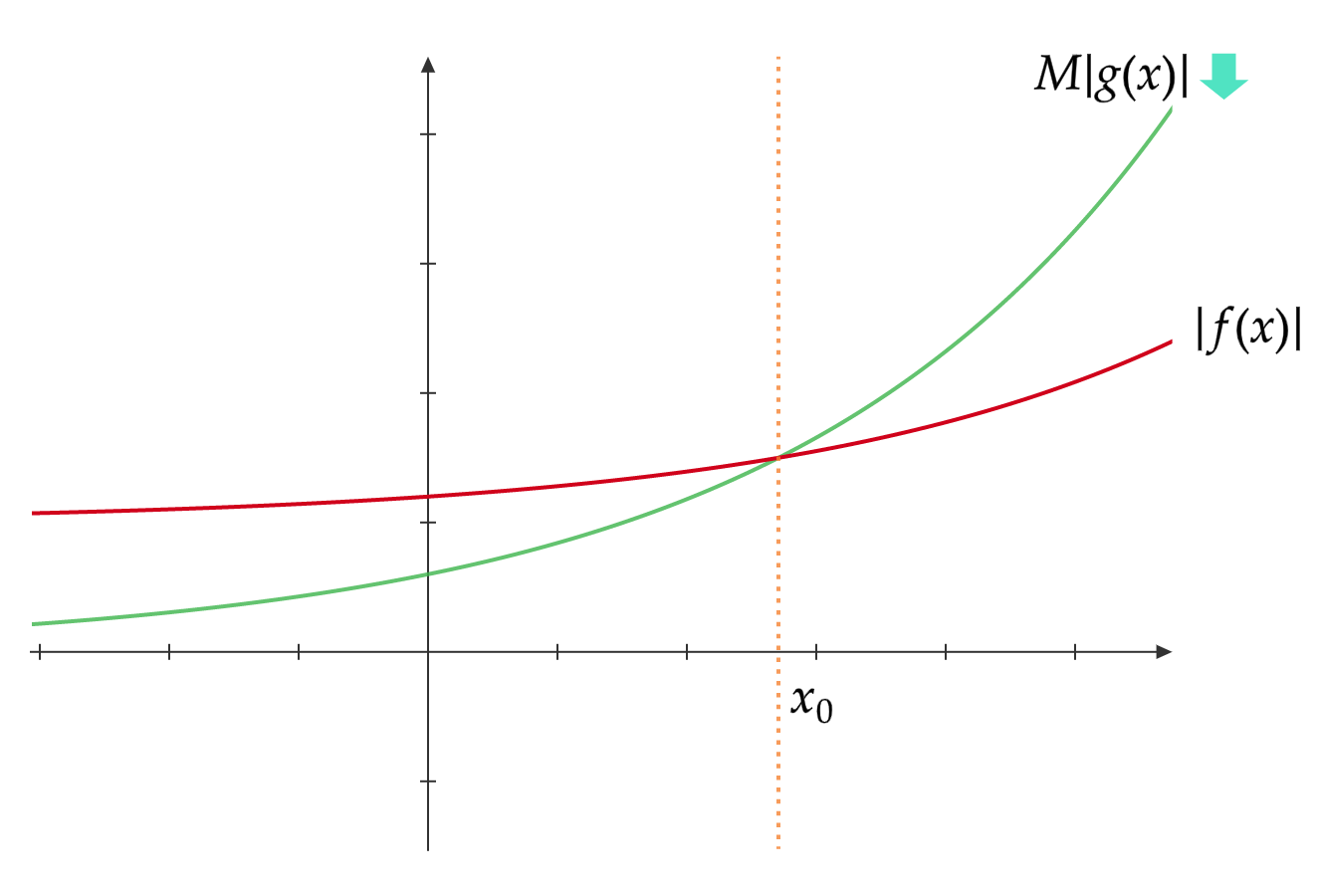
$f(x) \in o(g(x))$とは、
\forall M > 0, \exists x_0, \forall x > x_0 [|f(x)| \leq M|g(x)|]
が成り立つことである。
今までとは少し様子が違います。$|g(x)|$の係数である$M$に、存在記号$\exists$ではなく全称記号$\forall$がついています。これはつまりどんな$M$をとってきても$|f(x)| \leq M|g(x)|$となってしまうということなので、$f(x) \in o(g(x))$は$g(x)$をどんなによわくしてもいずれ$f(x)$を追い抜いてしまう、ということを意味します。
ちなみにこのことを「$g$が$f$を(漸近的に)支配する」というそうです。
スモール・オメガ
形式的定義は以下のようになります。
$f(x) \in \omega(g(x))$とは、
\forall M > 0, \exists x_0, \forall x > x_0 [|f(x)| \geq M|g(x)|]
が成り立つことである。
スモール・オミクロンの不等号の向きが変わっただけですね。つまり、$f(x) \in \omega(g(x))$は$g(x)$をどんなにつよくしてもいずれ$f(x)$に追い抜かれるということになります。
さっきとは逆で$f$の方が$g$を支配するわけですね。
まとめ
| オーダー | ざっくりとした意味 |
|---|---|
| $f(x) \in O(g(x))$ | $|f(x)|$は適当なだけつよくした$|g(x)|$にそのうち永遠に追い抜かれる。 |
| $f(x) \in \Omega(g(x))$ | $|f(x)|$は適当なだけよわくした$|g(x)|$をそのうち永遠に追い抜く。 |
| $f(x) \in \Theta(g(x))$ | $|f(x)|$は適当なだけつよくした$|g(x)|$にそのうち永遠に追い抜かれ、それでいて適当なだけよわくした$|g(x)|$をそのうち永遠に追い抜く。 |
| $f(x) \in o(g(x))$ | $|f(x)|$はどんなによわくなった$|g(x)|$にもそのうち永遠に追い抜かれる。 |
| $f(x) \in \omega(g(x))$ | $|f(x)|$はどんなにつよくなった$|g(x)|$もそのうち永遠に追い抜く。 |
似たような記号ばっかでどれがどれだか覚えづらいですが、これで明日から自慢できますね👍