概要
N個の正方形を辺でつなげた多角形はポリオミノと呼ばれる。例えば有名落ち物ゲームのテトリスでは N = 4 のポリオミノが用いられている。
N の増加に伴い、以下のようにポリオミノの数は指数関数的1に増えていく。
| N | 組み合わせ数(有向) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 19 |
| 5 | 63 |
| 6 | 216 |
| 7 | 760 |
| 8 | 2725 |
| ... | ... |
| 24 | 5239988770268 |
ポリオミノの数を算出する式を見つけるため、研究者らによりかなりの努力が行われてきたが、現状ではまだ発見に至ってはいない。
ポリオミノを列挙するアルゴリズムとして Redelmeier's algorithm というものがある。数え上げるので必然的に指数時間かかってしまうが、空間計算量は O(N) となるアルゴリズムである。
この記事では実際に JavaScript でアルゴリズムを実装し、これを視覚的に確認する。
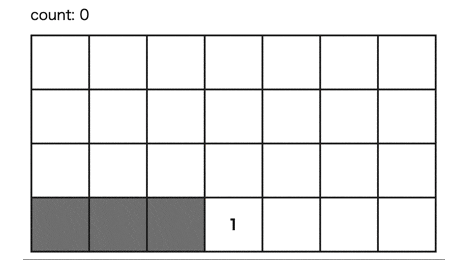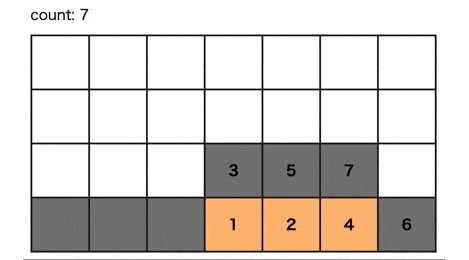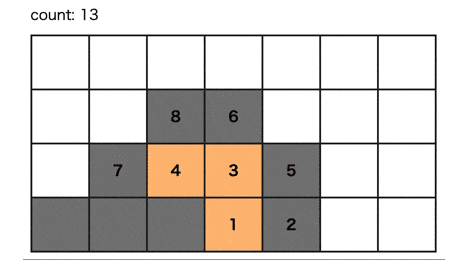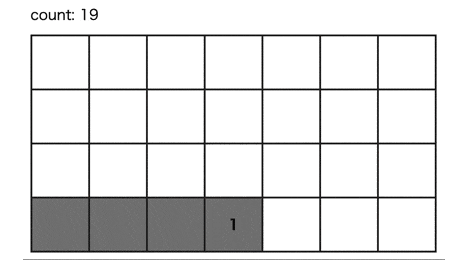
Redelmeier's algorithm
-
y > 0 or (y == 0 and x >= 0)となるようなセル空間を考える - [0, 0] に番号を振り
境界セルとする
境界セルを選択した際は以下作業を行う。
- 選択したセルの隣接セルの空いている箇所に辞書順(下左右上)に番号を振る
- 番号を振ったセルから1つずつ選択し
境界セルとする- ただし、既に
境界セルである最大番号より小さい番号のセルは選択しない
- ただし、既に
境界セルの選択を再帰的に深さ N まで行うことで、ポリオミノを列挙することができる。
実装
雑にアルゴリズムそのままに実装する。
ただ、後でステップ実行できるよう再帰のスタックは自前で用意しておく。
var N = 3;
var nodeStack = [
{
cells: [{ x: 0, y: 0, num: 1, isBorder: false }],
availableNumbers: [1]
}
]; // 状態を保持するスタック
function confirmBorderCellNumber(node, num) {
var cells = node.cells;
var cell = cells.find(e => e.num == num);
cell.isBorder = true;
var dx = [0, -1, 1, 0];
var dy = [-1, 0, 0, 1];
for (var i = 0; i < 4; i++) {
var x = cell.x + dx[i];
var y = cell.y + dy[i];
if (!(y > 0 || (y == 0 && x >= 0))) continue;
if (cells.find(e => e.x == x && e.y == y)) continue;
cells.push({ x: x, y: y, num: cells.length + 1, isBorder: false });
node.availableNumbers.push(cells.length);
}
}
function nextStep() {
var node = nodeStack[nodeStack.length - 1];
if (nodeStack.length > N || node.availableNumbers == 0) {
nodeStack.pop();
} else {
var num = node.availableNumbers.shift();
var newNode = JSON.parse(JSON.stringify(node)); // deep copy
confirmBorderCellNumber(newNode, num);
nodeStack.push(newNode);
}
}
// スタックが空になるまでステップ実行
var found = 0;
while (nodeStack.length > 0) {
nextStep();
// 葉(depth = N)の場合のみ出力
if (nodeStack.length > N) {
var node = nodeStack[nodeStack.length - 1];
var str = "";
for (var y = N - 1; y >= 0; y--) {
for (var x = 1 - N; x < N; x++) {
var cell = node.cells.find(e => e.x == x && e.y == y);
str += cell && cell.isBorder ? "#" : "_";
}
str += "\n";
}
console.log(++found);
console.log(str);
}
}
※ 計算量的に良くない実装なので、でかい N を調べたい場合うまく修正すること。
実行結果
1
_____
__#__
__##_
2
_____
_____
__###
3
_____
___#_
__##_
4
_____
_##__
__#__
5
_____
__##_
__#__
6
__#__
__#__
__#__
視覚化
1ステップずつ Web 上で実行できるようにしてみた。
N = 4 をステップ実行した様子の Gif はこんな感じ。
うまく重複を排除しているのが視覚的にわかる。
まとめ(+関係ない話)
この記事でやったこと
- Redelmeier's algorithm について簡潔に説明した
- Redelmeier's algorithm を JavaScript で実装し、ポリオミノの列挙を行った
- 列挙の様子をステップ実行できる Web サイトを用意した
調査に至る経緯
そもそも何故ポリオミノの列挙について調べたのかといえば、ぷよぷよの連鎖形の探索に使うためであった。(ぷよぷよの1連鎖は N >= 4 のポリオミノの形とみなせる。)
直接このアルゴリズムを役立てた訳ではないが、興味深い連鎖も見つかった。
2色4個消し16連鎖の動画https://t.co/PsPenGs7EW pic.twitter.com/o111yudFYv
— REF@ぷよ (@refpuyo) October 30, 2019
この動画では、手動で列挙した N = 4 のポリオミノ(テトロミノ)を使って連鎖組み合わせを探索した。ここで任意の連結数の連鎖を用いるためにポリオミノ列挙のアルゴリズムを使おうとしている。が、N が増えると連鎖の組み合わせが爆発的に増えるため、まだうまくいっていない。誰か助けてくれ…
参考
- ポリオミノの列挙 - phyllo’s algorithm note
- n-ominoの列挙(Redelmeier's algorithm) - matsu7874のブログ
- Handbook of Discrete and Computational Geometry —Third Edition—
-
実際は有向なNポリオミノ(fixed-n-omino)には $\lim_{n \to \infty} \frac{t(n+1)}{t(n)}$ であるような境界
λが存在し、それは大体 4 ちょっとになるらしい。ここで $t(n)$ は有向 $n$ ポリオミノの数。[Handbook of Discrete and Computational Geometry | THEOREM 14.3.2] ↩