グレイコード

グレイコード(gray code)とは

2進数の表現の一つである。数が1増減したときに常に1ビットしか変化しないという特徴がある。変化が1ビットのみなので、誤作動を起こしづらくなるため、ディジタル回路などに利用される。

バイナリコード

通常のコンピュータ上で扱う２進数表現のこと（10進数の3は2進数では11）

なぜ必要か

バイナリコードでは、数が増減する時、複数のビットが変化することがある。例えば７->８に変化する時は
0111
1000
なので、4ビット分変化することになる。ディジタル回路において、4ビット分変化する時、変化速度によっては0111->0000になる状態や0111->1111になる状態が存在することになり、誤ったデータとして処理してしまう可能性が高くなる。数が増減する時のビット変化をできるだけ少なくした方が誤作動を起こしにくくなる。

バイナリコードとグレイコード比較

十進数	Binary Code	Gray Code
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110

バイナリコードからグレイコードへの変換

グレイコードは、バイナリコードを右シフトし、XORを取ったものと定義する。

//BinaryCode -> GrayCode
unsigned int convertBinaryToGrayCode(unsigned int n) {
    return n ^ (n >> 1);
}

グレイコードからバイナリコードへの変換

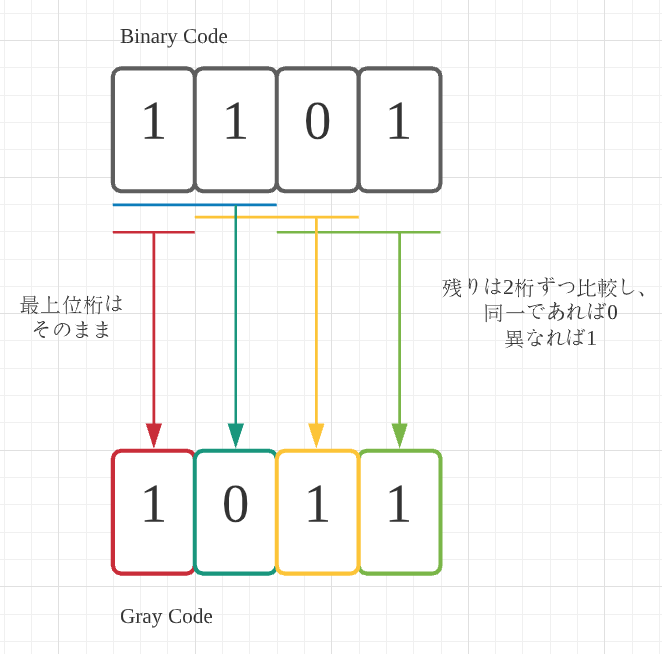
グレイコードからバイナリコードに変換する場合は以下の規則に従う。

1. 最上位桁の1は同一
2. 以下、上位から2桁ずつ見ていき、
3. 1か0が連続していればグレイコードは0、連続していなければ1とする。

という定義なのだが、コードで表現する際は以下のようにすればよい。

//GrayCode -> BinaryCode
unsigned int convertGrayToBinary(unsigned int n) {
    unsigned mask = n;
    while (mask) {
        mask >>= 1;
        n ^= mask;
    }
    return n;
}

確認用

1~10までをグレイコードに変換するコードを以下に記す。

#include <iostream>
#include <bitset>
#include <time.h>
using namespace std;
#define rep(i,s,n)for(ll i = s;i<n;i++)

//BinaryCode -> GrayCode
unsigned int convertBinaryToGrayCode(unsigned int n) {
    return n ^ (n >> 1);
}

//GrayCode -> BinaryCode
unsigned int convertGrayToBinary(unsigned int n) {
    int mask = n;
    while (mask) {
        mask >>= 1;
        n ^= mask;
    }
    return n;
}

int main() {
    int p = convertBinaryToGrayCode(13);
    int a[10];
    cout << "BinaryCode -> GrayCode" << endl;
    for (int i = 0; i < 10; ++i) {
        //変換
        a[i] = convertBinaryToGrayCode(i);
        //Bitsetを使用して表示
        cout << i << "=" << bitset<4>(i) << ":" << bitset<4>(a[i]) << endl;
    }
    cout << endl;

    cout << "Graycode -> Binarycode" << endl;
    for (int i = 0; i < 10; ++i) {
        //変換
        int x = convertGrayToBinary(a[i]);
        //Bitsetを使用して表示
        cout << bitset<4>(a[i]) << ":" << bitset<4>(x) << "=" << x << endl;
    }
}

実行結果

BinaryCode -> GrayCode
0=0000:0000
1=0001:0001
2=0010:0011
3=0011:0010
4=0100:0110
5=0101:0111
6=0110:0101
7=0111:0100
8=1000:1100
9=1001:1101
10=1010:1111

graycode -> binarycode
0000:0000=0
0001:0001=1
0011:0010=2
0010:0011=3
0110:0100=4
0111:0101=5
0101:0110=6
0100:0111=7
1100:1000=8
1101:1001=9
1111:1010=10