HL分解をそれとなく理解する

Heavy-Light-Decompositionを解説します。新規性や主張はありません。既存の記事を読んだ理解を書いたものです。

水色くらいの読者を対象にしていて、以下のような事前知識や経験が前提にあります。

• 木に対するクエリをいくつか解いたことがある。特に２点間の最短距離上のパスクエリ。
• 配列で区間クエリと区間更新。

なぜHL分解が必要か？

この記事の最初の２つがすべてです。木は更新に弱く、配列は更新に強いです。この記事ではこれをもう一歩かみ砕きます。まず、配列に対するクエリを考えます。

base: N個($10^5$程度)の要素からなる配列$A$があります。Q個のクエリが飛んできて($10^5$程度)ある２つの点$a, b$を与えるので、その閉区間の和を求めてください。
base2: 和でなくて、$min, max, gcd$などを求めてください
option: さらに、このクエリに$a_i$を$x$にupdateするクエリが飛んできます。

base, base2の問題は累積和、BIT, セグ木などで解くことができますし、optionの場合はセグ木で対応できます。このような配列に対する区間のクエリと更新は比較的（競技プログラミングでは）なじみ深いでしょう。ところが、これを木にすると難しくなります。つまり上記の問題を、

base: N個($10^5$程度)の要素からなる木$A$があります。Q個のクエリが飛んできて($10^5$程度)ある２つの頂点$a, b$を与えるので、その閉区間の和を求めてください。
base2: 和でなくて、$min, max, gcd$などを求めてください
option: さらに、このクエリに$a_i$を$x$にupdateするクエリが飛んできます。

とします。baseについてはクエリの条件によってDFSだけで対応できるものがあります。ところが、option、つまり、更新が入ったとたんに問題は難しくなります。

このような問題をHL分解で対応していきます。

HL分解の考え方

先ほどreferした記事に以下の記載があります。

列は更新にも変更にも強い構造です。

列の良さを木の構造でも使えるようにしましょう。

どういうことなの？(HL分解の「ような」概要)

さて、いま、以下のようなデータがあったとします。

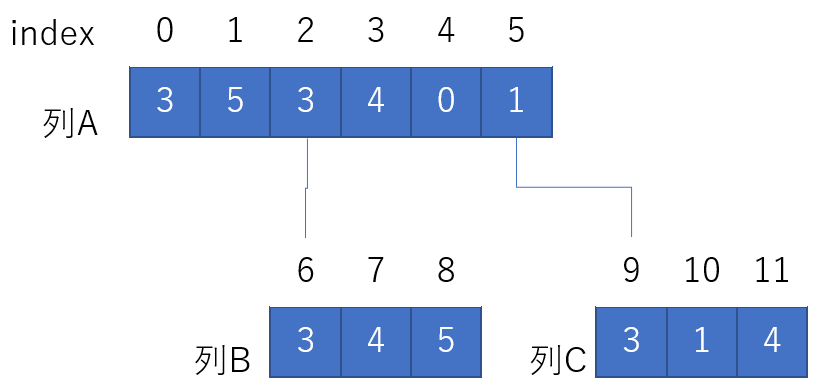
固まった列が３つあり、index2と6, index5と9はつながっています。このとき、ある2点が与えられたときのクエリを考えます。- クエリが同じ列内(つまり、0-5の間同士、6-8の間同士)であった場合、配列として事前計算・クエリできます。

では、違う列同士の点を選ぶとどうでしょう？index8と10の間を考えると次の区間を求めればいいことが分かります。

• 列Bの6-8の間の結果 + 列Aの2-5の間の結果 + 列Cの9-10の間の結果 (+は可算でなくて適当な演算としても良いです)

つまり、以下のようになります。

これを木にする

図を見て、木っぽいなと思ったかもしれませんが、まさに木です。「もし、分解した列の数が少なければ、どんなクエリが来てもある程度小さな計算量で済む」ので、そのような木を作っていきます。HL分解は以下の2つが肝になります。HL分解という名前から想像されるようにSTEP1の分解だけを実施...しても意味はなく、そのあとのSTEPを実行して初めて効果があります。(つまり、HL分解自身、で何か演算をするものではないです)

• STEP1: 木をHL分解する。複数の配列にする。(ただし、区間クエリ可能であることを前提とするので、複数の配列を一本につないだ配列を作る)
• STEP2: 2点のクエリを与える。2点間を通る列を特定する。
• STEP3: それぞれの列に対して、クエリし、結果を求めて返す。
• STEP4: 必要に応じて更新をする。
  • セグ木などを乗せていれば2点間の区間更新も可能です
  • 部分木への更新が容易に行えます。あるHLD上の配列の区間までは、(HLDを再帰で行っている場合)その部分木の情報となるので、クエリを行えます。どこまでがその部分木かは覚えておく必要がありますが、これはそのノードへのHLDが終わったときのHLD配列の長さを調べればよいので簡単です。

どう実現するか？

HLDパート

この記事の1, 2の前半がHL分解の方法です。

• DFSします。各ノードの深さと親と重さ(部分木のノード数)を記録します
• HLD分解をします。書いてある通りの実装を行っていきます。
  • あるノードを探索した時、新しくHLDの配列にpushします
  • Heavyなものを選び、自分と同じ列となるように再帰で呼びます
  • Heavy以外の子は、それら自身を新しい列の先頭となるように再帰で呼び出します

queryパート

クエリは２点を与えたときに、HLDした配列上でクエリをすべきリストを返します。また、これは列深いものから返します。先ほどを例にすると、

の場合は[9,10] [6, 8] [2,5]と返します。

• u, vに対して、その列が異なる場合、以下を繰り返します
  • 深い方のノードについて、その列の先頭までたどる情報を記録し、先頭の親に移動します
• これで、u, vは同じ列にいるので、最後にu, vをたどる情報を記録して終わりです
• この情報の記録では以下の点に気を付けます。このあと区間クエリを行うでしょうから、それぞれの記録では[a, b] で$a<=b$になるようにします。

利用側の気持ち

• queryパートの実装をするとqueryの結果をansと呼んだ時、ansの最後の要素のfirstはLCAです
• HLDパートを実施した後、Queryを呼ぶ前にHLD配列をセグ木などに入れておきます
• ansはHLD上の配列のIndexなので、そのまま（事前に作っておいた）セグ木などに入力します。ただし、この区間は閉区間[a,b]であるため、セグ木などにクエリする際には気を付けます。

実装(HL分解部分のみ)

/*
 * HeavyLightDecomposition(n)
 * HL分解をします。
 * 1: この構造を(n)で呼びます。nはノード数です。0-indexed。make_edge()で木を作ります
 * 2: hdl()を投げると、vector<int>(n)が返ってきて、これは[i] = j
 *    入力したiのノードはHLDの配列のjにマッピングされたということを示します
 * 3: 呼んだ側で、このマッピングをもとにたとえばセグ木など区間クエリできる構造体を作っておきます
 * 4: query(u, v)を呼ぶとvector<pair<int, int>が返ってきます。
 *    各pairの[a,b]はHLDの配列での「閉区間」のクエリを返します。
 *    これら全てに対して、seg.prod(a, b+1) (pairは閉区間なので適度にクエリしてください)します
 *    これらの結果は適切に結合します。
 */
/*
 * コード中でreal, hld のid/nodeという表記がありますが、
 * real: 入力時点での木のノード番号
 * hld: HLDの配列上のindex
 * を示します。
 */

struct HeavyLightDecomposition{
    int n;
    vector<vector<int>> g;
    vector<int> depthRealnode; // 実ノードの深さ
    vector<int> parentRealnode; // 実IDでの親(実ID)
    vector<int> childNumRealnode; // そのノードの重さ＝部分木のノード数。そのノード自身を1としてカウントします。
    vector<int> shallowRealnode; // ある実ノードに関して、その所属する列のもっとも浅いノード(実ID)
    vector<int> realid2hldid; // 実際のリストがHLDのいくつにマップされたのか？
    vector<int> hldid2realid;  // HLDリストの何は実際に何か？

    HeavyLightDecomposition(int n) : n(n) {
        g = vector<vector<int>>(n, vector<int>());
        depthRealnode = vector<int>(n, -1);
        parentRealnode = vector<int>(n, -1);
        childNumRealnode = vector<int>(n, 1); // ノードも重さは最初1
        shallowRealnode = vector<int>(n, 0);
        realid2hldid = vector<int>(n, -1);
        hldid2realid.clear();
    }

    void makeEdge(const int &u, const int &v){
        // u <-> v でedgeを張る
        assert(u != v);
        g.at(u).push_back(v);
        g.at(v).push_back(u);
    }

    // HL分解を行い、その結果の[real]=hldのマッピングを返します
    vector<int> hld(int rootRealnode, int topnode){
        dfs(rootRealnode, 0);
        _hld(rootRealnode, topnode);
        return realid2hldid;
    }

    // uRealnode,vの2点のパスを求めます。これはHLD上のIDで返されます。(何故なら、後で区間クエリ死体から)
    vector<pair<int, int>> query(int uRealnode, int vRealnode){
        vector<pair<int, int>> ansHldIDs;
        //同じ列状になるまで計算を続ける
        while(shallowRealnode.at(uRealnode) != shallowRealnode.at(vRealnode)){
            //cout << "real " << uRealnode << " " << vRealnode << " HLDworld: " << realid2hldid.at(uRealnode) << " " << realid2hldid.at(vRealnode) << "\n";
            //cout << " top(real):" << shallowRealnode.at(uRealnode) << "\n";
            // uRealnode,vそれぞれの最も浅いノードの深さ　が　浅い方をuにする
            // ※uRealnode, vRealnode 自身の深さの比較でないことに注意する
            // これによってrootの列にいるノードがさらに列を上らないようにします
            if(depthRealnode.at(shallowRealnode.at(uRealnode)) > depthRealnode.at(shallowRealnode.at(vRealnode))) swap(uRealnode, vRealnode);

            // 深い方は親をたどるので、{vRealnode, vの浅いノード} の区間を答えとして、vRealnodeを更新する
            ansHldIDs.push_back({realid2hldid.at(shallowRealnode.at(vRealnode)), realid2hldid.at(vRealnode)});
            vRealnode = parentRealnode.at(shallowRealnode.at(vRealnode));
        }
        // ここで、uRealnode, vはおなじ列に来たので、最後の処理を行う。区間クエリに備えて first <= secondで値を保存
        //cout << "finally real " << uRealnode << " " << vRealnode << " HLDworld: " << realid2hldid.at(uRealnode) << " " << realid2hldid.at(vRealnode) << "\n";
        //cout << " same top(real):" << shallowRealnode.at(uRealnode) << "\n";
        pair<int, int> lastEntry = {realid2hldid.at(uRealnode), realid2hldid.at(vRealnode)};
        if(lastEntry.first > lastEntry.second) swap(lastEntry.first, lastEntry.second);
        ansHldIDs.push_back(lastEntry);
        return ansHldIDs;
    }

    // HLDの前処理。各実ノードの深さと親を掘る
    // 計算量: O(N)
    void dfs(int root, int d) {
        depthRealnode.at(root) = d;
        for(int i = 0; i < (int)g.at(root).size(); ++i){
            auto nn = g.at(root).at(i);
        //for (const auto &nn: g.at(root)) { // 子ノードを見る
            if (parentRealnode[nn] != -1) continue; // 探索済みなら処理しない
            if (nn == parentRealnode[root]) continue; // 親には戻らない
            parentRealnode[nn] = root; // 次のノードの親は自分
            dfs(nn, d + 1);
            // DFS後、そのノードのノード数を自分に足す
            childNumRealnode.at(root) += childNumRealnode.at(nn);
        }
    }

    // HL分解をする。
    void _hld(int curRealnode, int topNode){
        //cout << "hld()" << curRealnode << " " << topNode << "\n";
        realid2hldid[curRealnode] = hldid2realid.size(); // 実際のノードの何がHLDリストの何番となるか？(次に配列に入るindexを得る)
        hldid2realid.push_back(curRealnode); // HLDID -> RealIDのマップ
        shallowRealnode.at(curRealnode) = topNode; // このノードの所属する最も浅い（＝列の先頭)のノード
        if(childNumRealnode.at(curRealnode) == 1) return; // 葉ならこれで終わり

        // ここから子の探索
        int maxVal = 0;
        int maxInd = -1;
        //for(auto nn: g.at(curRealnode)){ // 再帰が深いのでこの書き方はダメ
        for(int i = 0; i < (int)g.at(curRealnode).size(); ++i){
            auto nn = g.at(curRealnode).at(i);
            if(nn == parentRealnode.at(curRealnode)) continue; // 親は無視する
            if(childNumRealnode.at(nn) > maxVal){ // Heavyを探して更新。
                maxVal = childNumRealnode.at(nn);
                maxInd = nn;
            }
        }
        //cout << "heavy node:" << g[curRealnode][maxInd] << " val: "<< maxVal << "\n";
        _hld(maxInd, topNode);

        for(int i = 0; i < (int)g.at(curRealnode).size(); ++i){
            auto nn = g.at(curRealnode).at(i);
            if(nn == parentRealnode.at(curRealnode)) continue; // 親は無視する
            if(nn == maxInd) continue; // Heavyだった先も無視する
            _hld(nn, nn); // Lightを見ていく。この時、shallowNodeはそのノードとなる。
        }
    }
};

利用例: Library Checker: Vertex Add Path Sum

// HL分解典型
// https://judge.yosupo.jp/problem/vertex_add_path_sum
long long op(long long a,long long b){ return a+b; }
long long e(){return 0;}
void vertex_add_path_sum(){
    int n, q; cin >> n >> q;
    vector<int> dat(n);
    REP(i, n) cin >> dat.at(i);

    HeavyLightDecomposition hld(n);
    // 区間クエリ、1点可算可能ならば良いのでBITでも良い
    atcoder::segtree<long long ,op, e> st(n);
    REP(i, n-1){
        int u, v; cin >> u >> v;
        hld.makeEdge(u, v);
    }
    auto hldmap = hld.hld(0, 0);
    for(int i = 0; i < n; ++i) st.set(hldmap[i], dat[i]);
    while(q--){
        int type; cin >> type;
        if(type == 0) { // update p を x にする
            long long p, x; cin >> p >> x;
            // segtreeなのでp = [p, p+1) + xしている
            st.set(hldmap[p], st.prod(hldmap[p], hldmap[p]+1) + x);
        } else { // query
            int u, v; cin >> u >> v;
            auto ans = hld.query(u, v);
            long long ret = 0;
            for (const auto &[a, b]: ans) {
                // a,bはHLDのIDなのでそのまま食わせてよい
                ret += st.prod(a, b + 1);
            }
            cout << ret << "\n";
        }
    }
}

利用例: AOJ LCA

// LCA
// https://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=GRL_5_C&lang=jp
void GRL_5_C(){
    int n; cin >> n;
    HeavyLightDecomposition st(n);
    // 辺を貼る
    REP(i, n){
        int k; cin >> k;
        int x;
        REP(j, k){
            cin >> x;
            st.makeEdge(i, x);
        }
    }
    const auto &hldmap = st.hld(0, 0);
    //st.debugHLD();

    /*
     * HL分解を行ったあと、探索のリストの最後(ans.back)のfirstがLCAのノードである
     */
    int q; cin >> q;
    REP(i, q){
        int u, v; cin >> u >> v;
        //cout << "// " << u << ","<< v;
        auto ans = st.query(u, v);
        auto &[a, b] = ans.back();
        // ただし、HLD配列用のIndexになっているので戻して出力
        cout << st.hldid2realid[a] << "\n";
    }
};