Codeforces Educational Codeforces Round 101 C. Building a Fence 範囲を管理してYES/NO

https://codeforces.com/contest/1469/problem/C
正しく条件を読み、実装するだけ。といえばだけ。「今ブロックが置かれている可能性のある高さの上限と下限」を管理することで判定します。

概要

• nこのエリアに高さがちょうどkのフェンスを設置します。但し、地面は凸凹でゼロ以上の整数の高さ$h_1, h_2, ... h_n$が与えられます。
• このフェンスは宙に浮くことができます。ただし、以下のような制約があります。
• 1.設置するフェンスはすべて、前後のフェンスと１コマ以上接してないといけません
• 2.最初と最後(=$h_1$と$h_n$に設置されるフェンス)は地面に接していないといけません
• 3.フェンスはその地形の地面から$k$以上離れていてはいけません
• 4.その地形にめり込んではいけません(これは暗黙のルールです)

このような設置ができるかをYES/NOで答えてください

ルールの把握

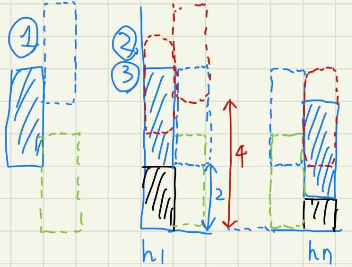
• 1: はシンプルです。図のように、１マスが被っていれば良いです。もし、前のフェンスの下を$x$とするならば、次のフェンスの下は$x - k - 1$が限界です(緑の破線)。次のフェンスの上は$(x + k) + (k - 1)$が限界です(青の破線)。

• 2: もシンプルです。$h_1$と$h_n$のフェンスは必ず地面に置かれます。つまり、$h_1$と$h_n$のエリアの赤い破線のように置くことはできず、青い四角の通り置かなければなりません。

• 3:は最も右の図に示すように、フェンスの高さが3だとするなら、その地形から2(これは$k-1$)以上はなれていてはいけません。

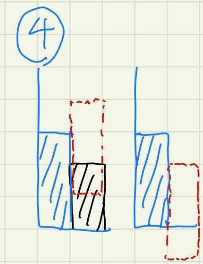
• 4: また、わざわざ説明されていませんが、以下の図のように地形にめりこんで配置してはいけません。

サンプルの把握

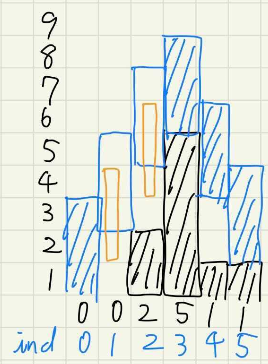
ここで、問題文中に紹介されている例を見てみます。sample1を次に示します。

黒い斜線部分は地面、青い斜線部分が確実に確定する部分です。青い線のみは例に書かれているフェンス。オレンジの線は例以外の候補です。

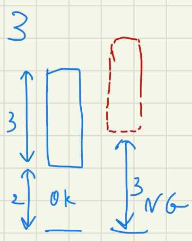
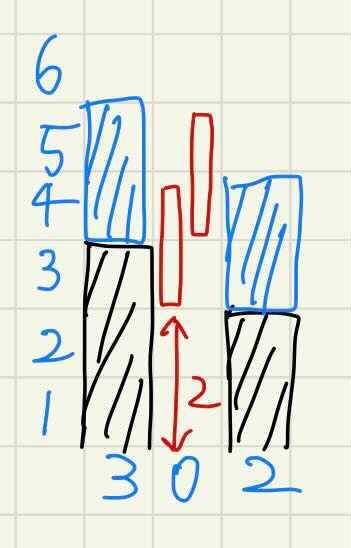
次に例3を見ます。青い斜線のフェンスはルール2により確定します。ルール1(フェンスが接していること)から、真ん中のフェンスは赤い四角のどちらかにフェンスを配置することはできません。しかし、ルール3により、このフェンスは地面(0)から2以上離れてはいけません(高さ2の位置から開始するフェンスはおけますが、それでは、最初のフェンスに届きません)

こう考えた

今の場所でフェンスが存在しうる高さを範囲として管理します。次のエリアに移動する際、今のフェンスと接続できる置き方ができるかを確認します。置くことが可能な場合、存在しうる高さを次のエリアに合わせて置き換えますが、条件に反しないような範囲とします。これを繰り返します。以降でこの手順を述べます

今のフェンスが存在しうる最低の高さを$curLow$, 最大の高さを$curHigh$とします。

• 0: まず、最初のフェンスが置かれるは確定なので、$curLow, curHigh$を$h_1 + 1, h_1 + k$とします。
• 1: 次のエリア$i$を見ます。次のエリアが最後のエリアの場合は5に飛びます。ここで確認すべきなのは、「2-1: 前のフェンスに届くか」と「2-2: 前のフェンスが地面より上にあるか」です。
• 2-1: 次のエリアで最も上までフェンスを届かせられるのは$h_i + (k-1) + k$です。$k-1$は地面から浮かせられる高さです。これが、$canLow$に届かない(未満)の場合、前のフェンスに届きません。このため、"NO"となります。
• 2-2: $canHigh$が$h_i$以下の場合、前のフェンスは今の地形に届いていないため、フェンスがおけません。このため、"NO"となります。
• 3: 前述の２項がクリアできた場合、フェンスを置くことができるので、$curLow, curHigh$を更新します。
• 4-1: curLowについて考えると、ルール1に伴い、$canLow - (k-1)$が地面を考えないときに配置できるフェンスの下限です。しかし、ルール4の通り地面にめり込んではいけません。このため、先の式より$h_i$の方が大きいか同じ場合、$h_i + 1$を$curLow$とします。$+1$しているのは、地面より１マス上げたところからしかフェンスは開始しないからです。
• 4-2: curHighについて考えると、ルール1に伴い、$canHigh + (k-1)$が配置できるフェンスの上限です。こちらについてはルール3が関係します。次のエリアでは2-1で述べたように浮かせられる高さには限界があります。なので、 $h_i + (k-1) + k$の方が低い場合、これを上限とします。
• 5: 最後のエリアでない場合、1に戻ります。最後のエリアはフェンスの配置する場所が$h_n + 1, h_n + k$で確定しています。このため、今の$curLow, curHigh$(つまり、最後から1つ前のフェンスが置かれうる位置)がこれと重なれるかを確認します。

実装

def do():
    n, k = map(int, input().split())
    dat = list(map(int, input().split()))
    # first wall
    canLow, canHigh = dat[0]+1, dat[0] + k-1+1
    for i in range(1, n-1):
        maxCurBlock = dat[i] + (k-1) + k
        if maxCurBlock < canLow: # current block can reach prev block?
            print("NO")
            return
        if canHigh <= dat[i]: # prev block cannot reach current ground?
            print("NO")
            return
        canLow = max(dat[i] + 1, canLow - (k-1))
        canHigh = min(maxCurBlock, canHigh + (k-1))
    # last wall
    if (canLow - dat[n-1]) > k:
        print("NO") # n-1 wall is too high
        return
    if canHigh <= dat[n-1]:
        print("NO") # last wall's ground is too high
        return
    print("YES")

q = int(input())
for _ in range(q):
    do()