Codeforces Round #650 Div.3 C. Social Distance 連続した0と1の個数処理

　概要

• n列の椅子があり、n文字の着席状況sが与えれられる。例えば、10001。1は着席。0は空席。
• ソーシャルディスタンスのため、必ず、空席をk個空けないと座れない。
• 今現在、ソーシャルディスタンスは保たれている。さて、あと最大で何人座れるか？

例

• k=1,で、100010の場合
  • さらに1人座れる。101010とできる。
• k=2で000000の場合
  • さらに2人座れる。100100とできる。
• k=1で10101の場合
  • もう座れない(0人)。10101にしかできない

こう考えた

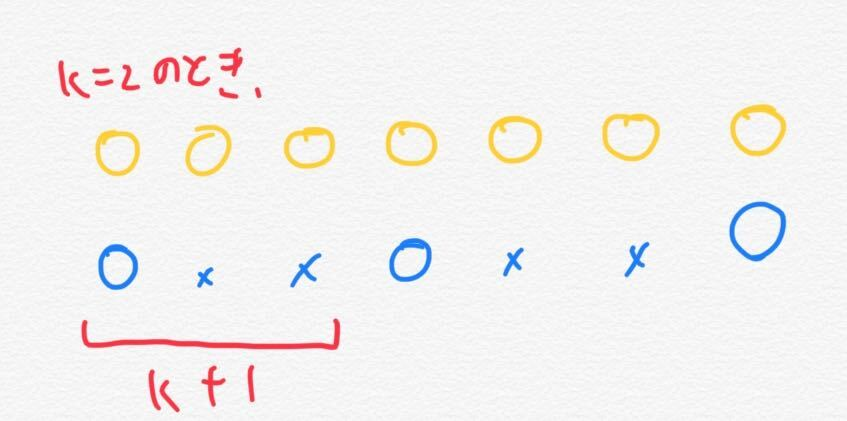
まず、このように誰もいない席がn=7あったとして、k=2と指定されたとする。この場合、ceil(n/(k+1))人が最大の着席数であることは図を書けば思い浮かぶ。なぜなら、まず左端に座り、k空けた後にこれを繰り替えすのが貪欲に最適だからである。

人が座れ売るのは0が連続する区間だけであり、どのように座ったところで隣の0が連続する区間には影響しない。つまり、各連続した0の区間について上の計算を行えばよい。

ところで、

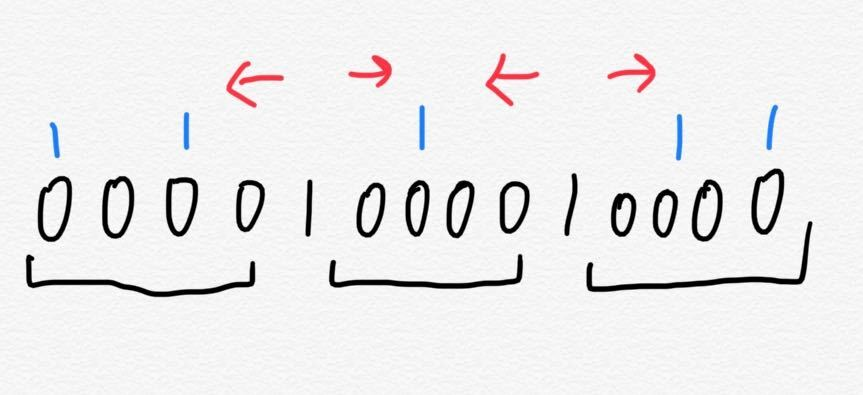
図のように、4つの空席が3つあることを考えると、両端は特殊な処理を行う必要がある。

• 真ん中のケースを考える。端でない連続した0の区間はその区間に含まれない1つ隣が1であることは自明である。そのため、両端は必ずkの距離を空けないとならない。
  • つまり、この区間は連続した0の数をlとすると、(l - k - k)の左端や右端にも1を置いていい区間と考えられ、上記のように計算できる。
• 例えば、左端のケースを考える。この場合、右側の1つ隣は1であるためkの距離を空けないとならない。ただし、左端は端なので、最も左に1を置ける。右端も同様である。

from pprint import pprint
import sys
 
import itertools
def countstrs(s):
    return [(k, len(list(g))) for k, g in itertools.groupby(s)]
import math
 
q = int(input())
for _ in range(q):
    n,k = map(int, input().split())
    s = input()
 
    res = 0
 
    dat = countstrs(s)
    #print(dat)
    l = len(dat)
    for i in range(l):
        ignoreLeft = False
        ignoreRight = False
        if i == 0:
            ignoreLeft = True
        if i == (l-1):
            ignoreRight = True
 
        if dat[i][0] == "1":
            continue
 
        cnt = dat[i][1]
        if ignoreRight is False:
            cnt -= (k)
        if ignoreLeft is False:
            cnt -= (k)
 
        #print("space", cnt)
        if cnt <= 0:
            continue
 
        res += math.ceil(cnt / (k+1))
 
    print(res)