LISの復元 (辞書順の最小となるLISを求める)

対象読者：DPで解くLIS長の求め方は分かる。けど、復元の方法がわからない。

今回の記事は、peroonさんの記事のソースコードを参考にしています。
https://perogram.hateblo.jp/entry/2019/07/27/051604

やりたいこと

長さ$N$の数列$A = a_{0}, a_{1}, \cdots, a_{N-1}$の最長増加部分列 (LIS: Longest Increasing Subsequence) のうち、辞書順最小であるものを出力してください。
数列Aの最長増加部分列は、$0 \leq i_0 < i_1 < \cdots < i_k < n$とするとき、、$a_{i_0} < a_{i_1} < \cdots < a_{i_k}$を満たすうち、$k$が最も大きいものです。
※つまり、狭義単調増加(厳密に増加する)のLISを考えます

間違った考察: DPテーブルだけで結果を求める

[7,8,9,4,5,6]という入力を考えると、LISは[4,5,6]か[7,8,9]が考えられます。LISをDPで計算した直後のDP配列は[4,5,6]となっており、一見、DP配列をそのまま出力すれば良さそうに思えます。

[7,8,9,4,5,6,1]という場合はどうでしょう。同じく、考えられるLISは[4,5,6]か[7,8,9]です。しかし、計算を終えた後のDP配列は[1,5,6]になっており、部分列になっていません。

LISとなる最後の更新(上記例では値6のupdate)の瞬間のDP配列を取ればよいでしょうか？別に、[1 2 6 9 5 10]を考えてみましょう。LISは[1 2 6 9 10]ですが、DP配列は、[1 2 5 9 10]となっています。

このように、DP配列見るだけでは、LIS復元さえ難しそうです。

考察1: LIS候補を考える

まず、LISの計算に使うDP配列は各数字が取りうる場所を二分探索で高速に見つけるための配列であり、必ずLISを成す状態でないことに注意します。DP配列はLISの候補となるメモであり、配列Aの部分列とは限りません。(ただし、部分列になることもあります)

ここで、LIS長$k$の配列Aを考え、あり得るLISを$ans$としましょう。

今、$dp[k]$が$a$という値で更新されたとき、$ans[k] = a$となり得るLISは存在します。なぜなら、dp[0]からdp[k-1]は配列Aの部分列ではないかもしれませんが、ここまでの値は全て、a未満であることが保証されているため(どのようにDPテーブルを作っているか思い出してください)、何らかの$k-1$までの部分列の後に$a$を追加したLISは存在します。

$ans[k]$が定目られるので、$k-1$までの存在する部分列が知りたいです。帰納的に考えます。$dp[k]$が$a$であるときの$ans[k-1]$を考えればよいです。これは、それ(dp[k]=aにした時)より前に$dp[k-1]$が更新されたときの値を使えばよいです。これを繰り返すことで、LISでありうる配列を生成することができます。

考察2: 辞書順最小を考える

$ans[k]$だけ考えます。DP配列の更新を考えると、$dp[k]$が最後に更新されたとき、$ans[k]$の値は最小です。これは、DP配列の計算より自明です。

これを帰納的に考えます。$ans[k-1]$の値を考えると、$ans[k]$が更新される一番直前に$dp[k-1]$を更新した値が$ans[k-1]$です。

実装

図で見ていきます。以下はDPを行う際のDP配列の遷移を図示しています。この際に、元の配列の各要素について、DP配列のどのindexに使ったかを記録していきましょう。(図左)

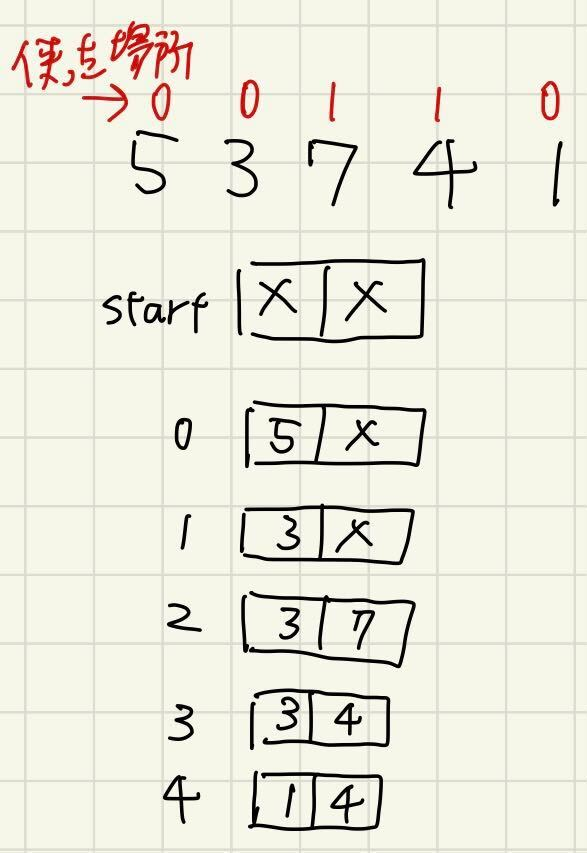
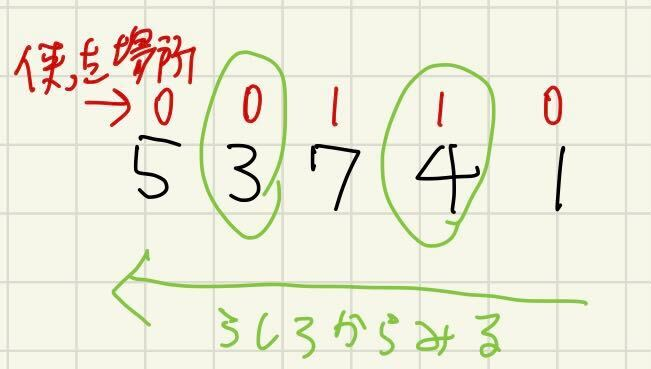
ここで、0-indexedなので、max(使った場所)+1がLIS長(=k)になります。
図右で復元していきます。まず、探したい値はtargetIndex=max(使った場所)です。後ろから見ていき、targetIndexが最初に見つかったら、それを、$ans[targetIndex]$に入れ、targetIndex--して、繰り返します。

最後はtargetIndex=-1を探す=絶対に存在しない、で左端まで走査してよいです。

これを繰り返せば、それより右側の選択が決まっているときの、ある桁のLISとなる最小の値が決定します。

計算量

時間計算量はLIS長を求めるのに$O(NlogN)$ 、復元に$O(N)$なので$O(NlogN)$です。
空間計算量は$O(N)$です。

実装例

この例では配列だけ返してLIS長は返していません。

inf = 2 ** 63

from bisect import bisect_left
def lis(l):
    # STEP1: LIS長パート with 使用位置
    n = len(l)
    lisDP = [inf] * n # 通常のLIS用リスト
    indexList = [None] * n # lの[i]文字目が使われた場所を記録する
    for i in range(n):
        # 通常のLISを求め、indexListに使った場所を記録する
        ind = bisect_left(lisDP, l[i])
        lisDP[ind] = l[i]
        indexList[i] = ind
    # STEP2: LIS復元パート by 元配列の使用した位置
    # 後ろから見ていくので、まずは、LIS長目(targetIndex)のindexListを探したいとする
    targetIndex = max(indexList)
    ans = [0] * (targetIndex + 1) # 復元結果(indexListは0-indexedなのでlen=4ならmax=3で格納されているので+1する)
    # 後ろから見ていく
    for i in range(n - 1, -1, -1):
        # もし、一番最後に出てきているtargetIndexなら
        if indexList[i] == targetIndex:
            ans[targetIndex] = l[i] # ansのtargetIndexを確定
            targetIndex -= 1
    return ans

print(" ".join(list(map(str, lis([7,8,9,4,5,6,1]))))) # 4 5 6
print(" ".join(list(map(str, lis([1,2,6,9,5,10]))))) # 1 2 6 9 10

#n = int(input())
#l = list(map(int, input().split()))
#print(" ".join(list(map(str, lis(l)))))

実装例(C++)

#include <bits/stdc++.h>
using namespace std;
#define FOR(i, begin, end) for(int i=(begin),i##_end_=(end);i<i##_end_;i++)
#define IFOR(i, begin, end) for(int i=(end)-1,i##_begin_=(begin);i>=i##_begin_;i--)
#define REP(i, n) FOR(i,0,n)
#define IREP(i, n) IFOR(i,0,n)
#define FASTIO() cin.tie(0); ios::sync_with_stdio(false)

int INF = 1e9+10;

int main(){
    int n; cin >> n;
    vector<int> l(n);
    REP(i, n) cin >> l.at(i);

    vector<int> lisDP(n, INF);
    vector<int> indexList(n, -1);
    REP(i, n){
        int ind = (int)distance(lisDP.begin(), lower_bound(lisDP.begin(), lisDP.end(), l.at(i)));
        lisDP.at(ind) = l[i];
        indexList.at(i) = ind;
    }
    int targetIndex = *max_element(indexList.begin(), indexList.end());
    vector<int> ans(targetIndex + 1);
    IREP(i, n){
        if(indexList.at(i) == targetIndex){
            ans.at(targetIndex) = l.at(i);
            --targetIndex;
        }
    }

    REP(i, ans.size() - 1) cout << ans.at(i) << " ";
    cout << ans.at(ans.size() - 1) << "\n";

}