最大マッチングなの!?という問題。想定解ではDSU解が紹介されていたので別解としての記録記事。
題意
最大マッチングとして良く出てくる典型的な結婚問題として言い換えます。
- N人の人が(このN人とは別の)$410^5$人の相手に求婚しようとしています。$(1 \leq N \leq 210^5)$
- 各N人は2名$(a, b)$に求婚する($a=b$の事もあります)。
- 求婚された側は1人としか結婚できません。
- 結婚が成立する最大のペアは何組か?
アプローチと実装のアプローチ
最大マッチングとして考えます。
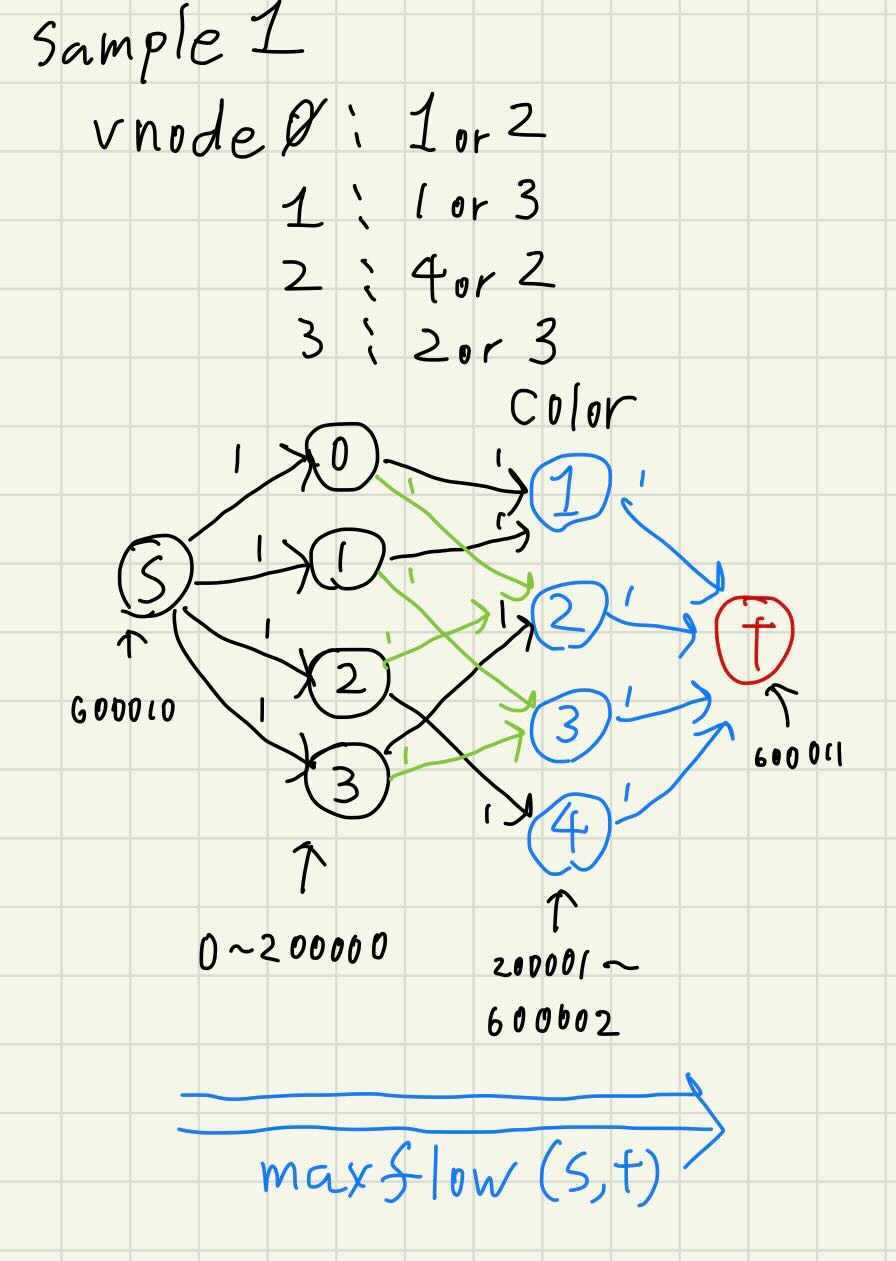
図のように左右にソース$s$とゴール$t$を用意します。二部グラフの左側はカードのノードで右側を書かれた値のノードとして作ります。
ソース$s$から各カード(左の各ノード)に1の流量を流します。これで左のノードは右のノードに1しかフローを流せません。(つまりどちらの値にしかフローを流せません)
カード(左)のノードからはそれぞれの$a,b$である右のノードに対して流量1の辺を張ります。$a=b$の場合、片方にしかフローは流せないので2本の辺を張って良いです。
全右のノードからは$t$に対して流量1の辺を張ります。たくさんの左のノードから選ばれても$t$には1しか流せません。
$t$に到達できるフローは、何らかの左側のノードからの入力がもらえる右側のノードの数(各流量は最大1なので)と言えます。
$s -> t$のmax-flowが答えです。結婚問題での成立したペアの数です。
実装
#include <bits/stdc++.h>
#include <atcoder/all>
#define FOR(i, begin, end) for(int i=(begin),i##_end_=(end);i<i##_end_;i++)
#define REP(i, n) FOR(i,0,n)
using namespace std;
using namespace atcoder;
const int numNode = 2*100000;
const int numColor = 4 * 100000;
const int numGraph = numNode + numColor + 100;
const int snode = numGraph - 3;
const int tnode = numGraph - 2;
int main(int argc, char *argv[]) {
int n, a, b;
cin >> n;
mf_graph<int> mf(numGraph);
REP(i, n){
cin >> a >> b;
a += numNode; b += numNode;
mf.add_edge(snode, i, 1);
mf.add_edge(i, a, 1);
mf.add_edge(i, b, 1);
}
FOR(i, numNode, numNode + numColor + 2){
mf.add_edge(i, tnode, 1);
}
cout << mf.flow(snode, tnode) << endl;
}