Codeforces Round #674 Div. 3E. Rock, Paper, Scissors を最大流で解く

最大流に興味を持ったきっかけの問題です。

題意

• じゃんけんをします。グーチョキパー(G, S, P)があります。
• AさんとBさんがいて、n回試合をします。G,S,Pをそれぞれ、Ag, As, Ap回とBg, Bs, Bp回出します。(n試合なので互いの和はnです)
• あいこは引き分けです。
• Aさんが勝利する最大の数と最小の数を答よ

考え方

まず、問題を以下のように言い換えます。

• Aさんが勝利する最大の数と最小の数をこたえよ
• Aさんが勝利する最大の数と「n から 負け　か　あいこにできる最大の数を引いた回数」をこたえよ

次のように２つのグラフを作ります。

ポイントは各手同士の辺のcapは無限大とすることです。(本題意において、各手の数をcapとしても良いですが、問題として考える際に、capを制限する必要はなく、infとして扱ってよいです)

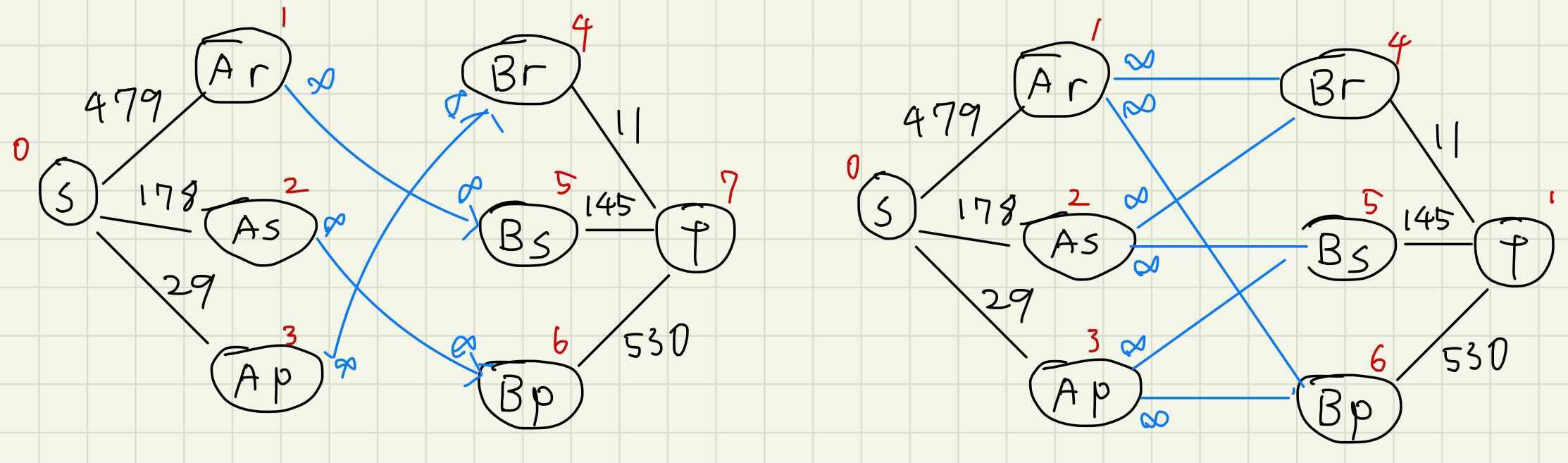
まず、左が勝利する最大の勝つ回数を求めるグラフです。

• 0,7を始点終点として、その他のノードは図のように各手のノードだとします
• スタート地点からAの各ノードに対してcap = 出せる手数とした辺を張ります
• 同様に、Bの各ノードからcap = 出せる手として辺を張ります
• A勝てる組み合わせの手(AグーならBチョキなど)に辺をはり、このcapは無限大とします。

sからtの最大流がAが勝てる最大の数です。

次に、右が「負け　か　あいこになる最大の数」を求めるグラフです。

• グラフの構成は同じです。
• A,B間の手の張り方が異なり、Aがあいこか負けになる手(Aグーなら、BグーあるいはBパー)に辺をはり、このcapは無限大とします。

sからtの最大流mfがAが「負け　か　あいこになる最大の数」です。なので、n - mf がAが勝利する最小の数です。

実装

ACL部分は省略します。

int main(int argc, char *argv[]) {
    mf_graph<ll> mfwin(8);
    mf_graph<ll> mflose(8);
    ll n,ar,as,ap,br,bs,bp;
    cin>>n>>ar>>as>>ap>>br>>bs>>bp;
    ll inf = 1e12;
    ll reswin, reslose;

    // 勝つ回数
    mfwin.add_edge(0, 1, ar); mfwin.add_edge(0, 2, as); mfwin.add_edge(0, 3, ap);
    mfwin.add_edge(4, 7, br); mfwin.add_edge(5, 7, bs); mfwin.add_edge(6, 7, bp);
    mfwin.add_edge(1, 5, inf);
    mfwin.add_edge(2, 6, inf);
    mfwin.add_edge(3, 4, inf);
    reswin = mfwin.flow(0, 7);
    // あいこ　か　まけ　の回数
    mflose.add_edge(0, 1, ar); mflose.add_edge(0, 2, as); mflose.add_edge(0, 3, ap);
    mflose.add_edge(4, 7, br); mflose.add_edge(5, 7, bs); mflose.add_edge(6, 7, bp);
    mflose.add_edge(1, 4, inf); mflose.add_edge(1, 6, inf);
    mflose.add_edge(2, 4, inf); mflose.add_edge(2, 5, inf);
    mflose.add_edge(3, 5, inf); mflose.add_edge(3, 6, inf);
    reslose = mflose.flow(0, 7);

    cout << n - reslose << " " << reswin << "\n";
}