オイラーツアーした木に対するクエリ

この記事に新規性はありません。maspyさんの記事、beetさんの記事がとても分かりやすいです。また、紹介しているテクニックはmaspyさんの記事で紹介されているものです。
maspyさんの記事: Euler Tour のお勉強
beetさんの記事: 2種類のEuler Tourについて

オイラーツアーとは？

根付き木を根からDFSして根に戻ってくるような経路（の探索）。競技プログラミングの文脈ではこの行きと戻りの経路について以下のような情報を記録しておくきRMQやRSQを適応することで木に対するいくつかのクエリを高速に処理できる。

• 1. 各頂点のinとoutの時刻
• 1. それまでに辿った辺や頂点の重さなどの情報を記録
• 1. 各頂点の深さの情報

用語

• 行きがけ: あるノードから子に移動する
• 帰りがけ: 子からその親ノードに移動する

実際の例

1を根とする以下の木があるとします。

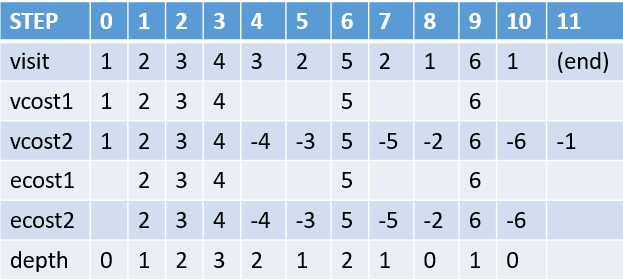
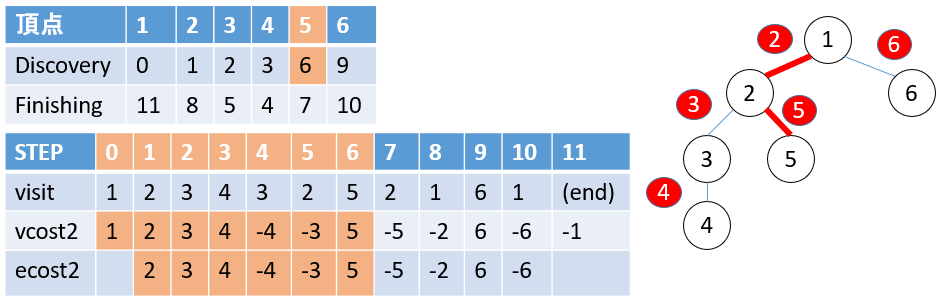
時刻0は根である1にいてDFSで木を探索します。探索する際に以下のように値を記録しておくことにします。戻りがけの

visit: STEPで訪れた頂点の番号
vcost1: 初めて訪れた際のその頂点のコスト(本例では頂点コストは頂点番号に等しくしている)
vcost2: 初めて訪れた際のその頂点のコスト と 最後に訪れた際のコストをマイナスで記録したもの
ecost1: 初めて通った辺のコスト
ecost1: 初めて通った辺のコスト と 最後にその辺を訪れた時のコストをマイナスで記録したもの
depth: その頂点の深さ

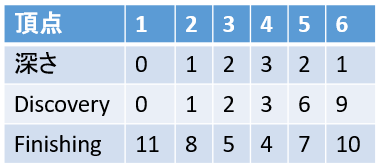
同時に各ノードごとに以下を記録しておきます。後述のとおりこれを記録しておくとそのノードを根とする部分木

深さ: 根を0とした時の頂点の深さ
Discovery: その頂点を最初に訪れた時間(STEP)
Finishing: その頂点を抜けた時間(STEP) つまり、その頂点を最後に訪れた時間+1

$Finishing$は「最後に訪れた時間」ではなく「抜け終わった時間」です

これらを使うことでいくつかの根付き木へのクエリを以下のように解けます。

LCA

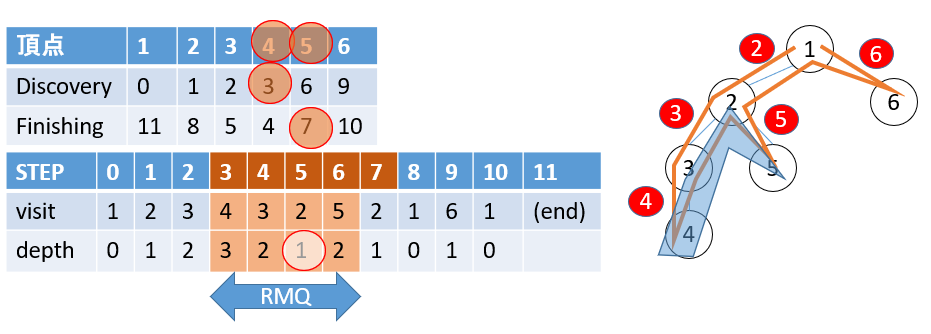
頂点$x,y$のLCAを求めたい場合、それらの$Discovery, Finishing$のminとmaxを$a,b$としたとき、 $depth$の区間$[a, b)$(閉区間、開区間)に対してRange Min Queryを行ってそのノード番号を調べれば良いです。

• 例1: $LCA(4,5) = 2$
  

$a,b$の区間は図上の青で囲った通り、片方のノードに入り、もう一方のノードを出るまで(パターン1と呼ぶ)の区間を表ます。
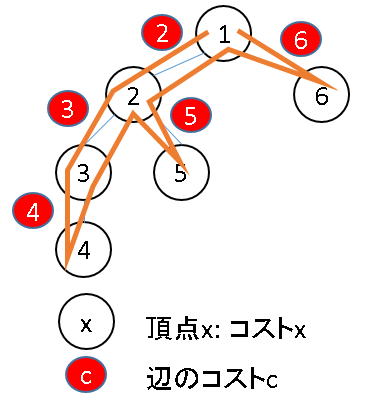
LCAを考えると、「片方のノードから上にたどって、もう一方のノードに上から到着するまでの最も深い共通の頂点」を選択したくなるが、LCAをとるうえでは片方のノードから下にたどった区間を入れても良いです。例えば、以下のような木で考えます。

左「青に入って黄色に出るまで」と右「青を出て黄色に出るまで」は含まれる範囲がことなります。違いは、それぞれを根とする部分木を含むかどうかですが、それらを根とする部分木はそれらより深い頂点しか含みえないため、LCAを考える上では影響がありません。

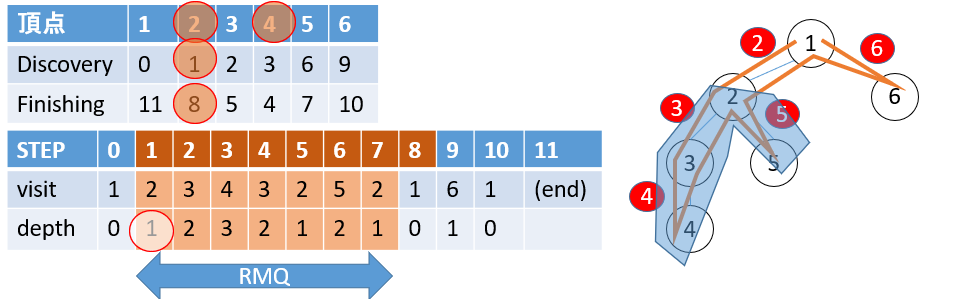
• 例2: $LCA(2,4) = 2$
  それでは、一方の頂点が祖先である場合を考えます。

一方の$DiscoveryとFinishing$の間はその部分木であり、その一方の路にもう一方の頂点は含まれるからである。

頂点xを根とする部分木の頂点のコストと辺のコストの合計

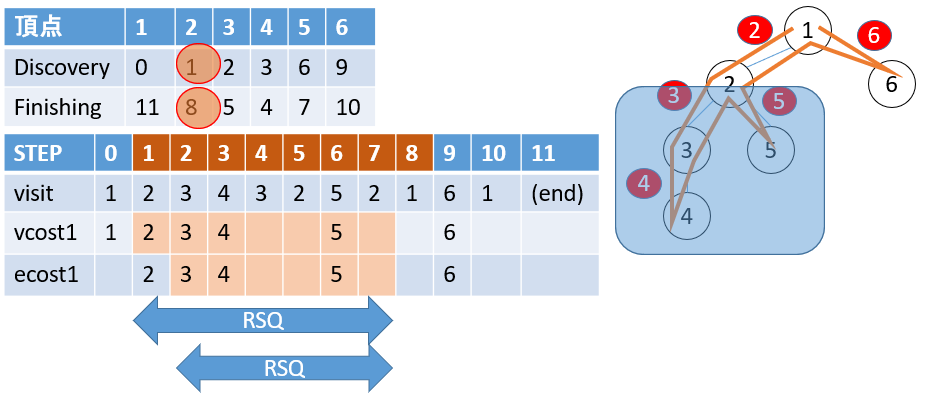
図の通り、頂点$x$の$Discovery, Finishing$を$d,f$としたとき、

• 頂点の合計は$vcost1$の$[d,f)$ (閉区間、開区間)
• 辺の合計は$ecost1$の$(d,f)$ (開区間、開区間)
  のRange Sum Queryで求められます。

今回は、$index 4,5$のような戻りの経路も保持しているので難しいのですが、行きのコストをだけを持つようにテーブルを作成し、$Discovery, Finishing$もそれらを参照するようにすれば、Range Sum Updateが可能になり、部分木中のすべての辺や頂点のコストをupdateすることも簡単にできます。

根からのパスクエリ(最短経路での辺と頂点の和)

とても賢いなと感じたのですが、上記の$ecost1$, $vcost1$に対して、戻るときにそのマイナスのコストを記録したものを$ecost2$, $vcost2$とします。すると

• 頂点の合計は$ecost1$の$[0,d]$ (閉区間、閉区間)
• 辺の合計は$vcost1$の$(0, d]$ (開区間、閉区間)
  のRange Sum Queryで求められます。

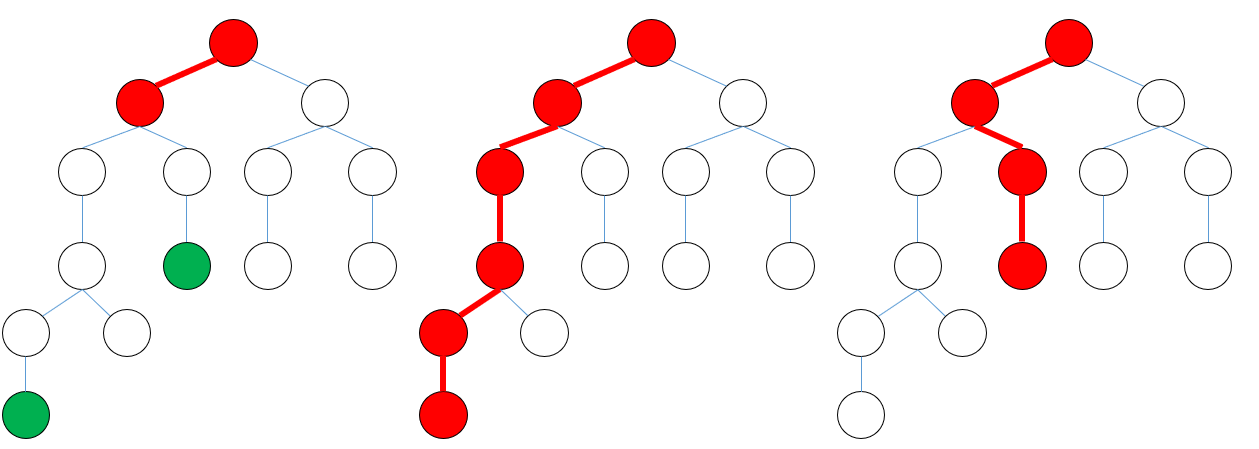
少し深い木を考えてみます。

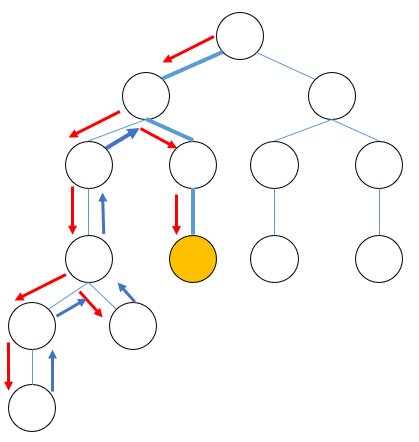
求めたい頂点までのパスクエリが青い辺だとすると、そこまでのRSQは（例えば辺について考えると）赤が加算、青が減算でちゃんとキャンセルされていることがわかります。

任意の２点間の距離

ところで、根からのパスクエリができると、任意の２頂点間のコストを求めることができます。
2頂点$x,y$とそのLCA$a$があり、任意の点zに対する根からの辺のパスクエリを$pe(z)$ ,頂点のパスクエリを$pv(z)$とすると、

• 頂点の合計は $pv(x) + pv(y) - 2pv(a) + (頂点aのコスト)$
• 辺の合計は $pe(x) + pe(y) - 2pe(a)$

です。これを図で示します。

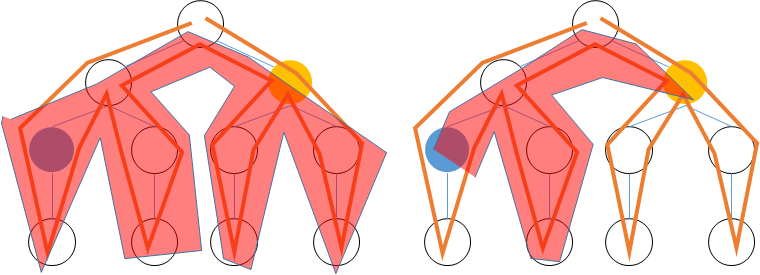
例えば、左の緑の２点の間の辺と頂点のコストを求めたいとします。この２段目の赤い点がLCAの頂点です。それぞれの頂点へのパスクエリは真ん中と右の図のような頂点と辺を含みます。この図と上記の式を見比べると一致することがわかります。
頂点のコストを計算する場合、祖先を２回消してしまうので、足しなおします。

ソースコード

上記までの文章と異なり、辺のコストを$1,2,4,8,16$,頂点のコストを$1,10,100,1000,10000,100000$としています

"""
   0
   |
 +-+--+
 1    |
|+|   |
2 4   5
|
3
"""
import sys

sys.setrecursionlimit(100000)

N = 7
G =[None] * N
# (next, cost)
G[0] = []
G[1] = [(2,1),(6,16)]
G[2] = [(3,2),(5,8)]
G[3] = [(4,4)]
G[4] = []
G[5] = []
G[6] = []

vertexCost = [None] * N
vertexCost = [-100, 1, 10, 100, 1000, 10000, 100000]

S = []
F = [0]*N
depth = [0]*N

# PreOrder(先行順巡回) 0 -> 1と追うやつ。典型。
from collections import deque
q = []
path = []
pathdepth = []
vertexCost1 = []
vertexCost2 = []
edgeCost1 = []
edgeCost2 = []

rootnode = 1
depth = [-1] * N
nodein = [-1] * N
nodeout = [-1] * N
q.append([rootnode, 0, 0, vertexCost[rootnode]])
curtime = -1
usedPreorder = [False] * N
preorder = []
postordercnt = [-1] * N
postorder = []
parent = [None] * N

# q: nodenum, depth, vcost
while len(q) != 0:
    curtime += 1
    curnode, curdepth, vcost, ecost = q.pop()
    if curnode >= 0: # 行き掛け
        if nodein[curnode] == -1:
            nodein[curnode] = curtime
        depth[curnode] = curdepth
        pathdepth.append(curdepth)
        path.append(curnode)
        edgeCost1.append(vcost)
        edgeCost2.append(vcost)
        vertexCost1.append(ecost)
        vertexCost2.append(ecost)
        if len(G[curnode]) == 0: # 子がいないときの処理
            nodeout[curnode] = curtime + 1
        for nextnode, nextvcost in G[curnode][::-1]:
            print("! ", nextnode, vcost)
            if depth[nextnode] != -1:
                continue
            q.append([~curnode, curdepth, nextvcost, -vertexCost[nextnode]])
            q.append([nextnode, curdepth + 1, nextvcost, vertexCost[nextnode]])
            parent[nextnode] = curnode
    else: # もどりがけ
        curnode = ~curnode
        if nodein[curnode] == -1:
            nodein[curnode] = curtime
        path.append(curnode)
        edgeCost1.append(0)
        edgeCost2.append(-vcost)
        vertexCost1.append(0)
        vertexCost2.append(ecost)
        pathdepth.append(curdepth)
        nodeout[curnode] = curtime + 1

# last
path.append(-1)
pathdepth.append(-1)
vertexCost1.append(0)
vertexCost2.append(-vertexCost[rootnode])
edgeCost1.append(0)
edgeCost2.append(0)

print("Parent:", parent)
print("Nodein:", nodein)
print("Nodeout:", nodeout)
print("Path:", path)
print("Depth", pathdepth)
print("vcost1", vertexCost1)
print("vcost2", vertexCost2)
print("ecost1", edgeCost1)
print("ecost2", edgeCost2)
#######
# 試験なので、疑似RMQ(実際はseg treeなど組む)
def rmq(a, l, r):
    resind = -1
    resval = 2**64
    for i in range(l, r):
        if a[i] < resval:
            resval = a[i]
            resind = i
    return resind

def rsq(a, l, r):
    return sum(a[l:r])

def lca(x, y):
    l = min(nodein[x], nodein[y])
    r = max(nodeout[x], nodeout[y])
    ind = rmq(pathdepth, l, r)
    return path[ind]

def subtreeVertexCost(x):
    l = nodein[x]
    r = nodeout[x]
    return rsq(vertexCost1, l, r)

def subtreeEdgeCost(x):
    l = nodein[x]
    r = nodeout[x]
    return rsq(edgeCost1, l + 1, r)

def pathQueryFromRootVertexCost(x):
    return rsq(vertexCost2, 0, nodein[x] + 1)
def pathQueryFromRootEdgeCost(x):
    return rsq(edgeCost2, 0, nodein[x] + 1)

def pathQueryVertexCost(x, y):
    a = lca(x,y)
    return pathQueryFromRootVertexCost(x) + pathQueryFromRootVertexCost(y) - 2 * pathQueryFromRootVertexCost(a) + vertexCost[a]
def pathQueryEdgeCost(x, y):
    a = lca(x,y)
    return pathQueryFromRootEdgeCost(x) + pathQueryFromRootEdgeCost(y) - 2 * pathQueryFromRootEdgeCost(a)



# LCA(4, 5) = 2
print(lca(4, 5))
# LCA(2, 4) = 2
print(lca(2, 4))

# subtreeEdgeCost(1)=111111
print(subtreeVertexCost(1))
# subtreeVCost(1)=31
print(subtreeEdgeCost(1))

# subtreeEdgeCost(2)=11110
print(subtreeVertexCost(2))
# subtreeVCost(2)=14
print(subtreeEdgeCost(2))

# subtreeEdgeCost(4)=1000
print(subtreeVertexCost(4))
# subtreeVCost(4)=0
print(subtreeEdgeCost(4))


print(pathQueryFromRootVertexCost(5))
print(pathQueryFromRootEdgeCost(5))

print(pathQueryFromRootVertexCost(6)) # 100001
print(pathQueryFromRootEdgeCost(6)) # 16

print(pathQueryVertexCost(3,5)) # 10110
print(pathQueryEdgeCost(3,5)) # 10

print(pathQueryVertexCost(2, 2)) # 10
print(pathQueryEdgeCost(2 ,2 )) # 0

print(pathQueryVertexCost(4,6)) # 101111
print(pathQueryEdgeCost(4,6)) # 23