一部で有名になった以下のYouTubeの問題の解法を簡単に説明します。加えて時間・空間計算量を実験します。
3つ目の解法で主人公が使うフロイドの循環検出法は少しだけ詳しめに説明します。
まず、Pythonで考察と実験を行った後、Cで同様の試験を行い、比較します。
以下のYouTubeを見てからの方が楽しく記事が読めます

↑ Youtube: If Programming Was An Anime
https://leetcode.com/problems/find-the-duplicate-number/
元ネタはこれです(改変があります)
結論を先に
- 辞書は速いがメモリを思っているより多く使用する
- フロイドの循環検出法は$O(N)$だが(他の2つに比べると)定数倍は重い。ただし、メモリ使用量がO(1)
題意
- 整数$N$が与えれます。また、$N+1$個の要素からなるリスト$A$が与えられる。
- $A$の要素は$1からn$の整数が1つだけ出現する。ただし、ある整数だけ2個以上含まれることが保証される。
- 重複している整数を述べよ
具体例
例: $[3,1,3,4,2]$といった入力が考えられる。この場合、$3$を答える。
例: $[2,2,1,2,2]$といった入力が考えられる。この場合、$2$を答える。
例: $[1,3,2,1]$といった入力が考えられる。この場合、$1$を答える。
例: $[1,1]$といった入力が考えられる。この場合、$1$を答える。
アプローチ1: ソートと線形探索
主人公が最初に行ったアプローチは
- (a)昇順にソートを行い, (b)先頭から線形操作して2つずつ要素を見ていき、重複を見つけ出す

空間計算量は$N$であるが、時間計算量はaの処理に$N log N$かかり、bに$N$かかってしまい、結果、計算量がTLEしてしまいました。
from typing import List
def findDuplicate(nums: List[int]):
nums.sort()
for i in range(len(nums) -1):
if nums[i] == nums[i+1]:
return nums[i]
print(findDuplicate([1,1])) # -> 1
print(findDuplicate([3,1,3,4,2])) # -> 3
アプローチ2: HashMap-Uh!
ついに、主人公は自分だけでは制御できないほどの力が必要となるHashMap-Uh!(つまり辞書)を使います。
- (a)まず辞書を初期化し、(b)数字を順にみて既に辞書に存在しているならそれが重複する数
- (c)重複しない数字なら存在済みとして値を記録
結果、MLE(メモリ使用量エラー)が起きます。
そんな馬鹿なという気もしますが、確かに、辞書はメモリを要素数以上に使用します。以下のコードで見てみます。
from typing import List
from sys import getsizeof
def findDuplicate(nums: List[int]):
used = dict()
for x in nums:
if x in used:
size = getsizeof(used) + sum(map(getsizeof, used.values())) + sum(map(getsizeof, used.keys()))
print("Memory:", size)
return x
used[x] = True
print(findDuplicate([1,1])) # -> 1
print(findDuplicate([3,1,3,4,2])) # -> 3
print(findDuplicate(list(range(1,1000000+1)) + [1000000]))
これを実行すると、
Memory: 156 (Byte)
1
Memory: 184 (Byte)
3
Memory: 55100346 (大体55M Byte)
1000000
ということで要素数に対して大きなメモリを使用しています。
$N=10^{6}$の入力に対して$55M$のメモリなので、$N=2 \cdot 10^{6}$でメモリ$64M$だとデータ量だけで$MLE$してしまいますね。
【独自】アプローチ2改: 辞書からリストによる利用履歴
辞書は思った以上にメモリ空間を利用することが分かりました。ほかのアプローチとして、あらかじめ$1-N$の配列を作成し、$False/True$で出現したかどうかを比較するアプローチが考えられます。このアプローチは後の実験で評価に用います。
実装としては以下のようになります。
def findDuplicate22(nums: List[int]):
used = [False] * len(nums)
for x in nums:
if used[x]:
return x
used[x] = True
アプローチ3: フロイドの循環検出法
ここでセンパイが登場します。センパイはクールにFloyd's cycle-finding algorithmを提案します。
説明のため、この問題文は以下のように読み替えます。(これは元の問題と全く同じ入力と出力になります)
- この世界にはn個の街があり、それぞれにはテレポータがある
- $n+1$個の整数からなる配列$a$が与えられる。この配列は1からnの整数が0個か1個含む。しかし、ただ1つの数だけは複数個含まれる。
- 今あなたは街0にいる。
- あなたはi($0 \leq i \leq n$)の街にいるとき次は$a_{i}$の街にテレポートする
- あなたは同じ街に2度訪れたならば、その街でテレポートをやめる。この街はどこか?
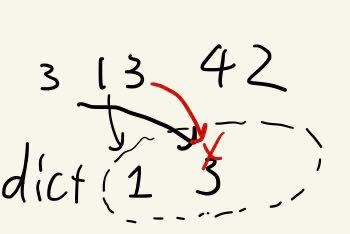
例として、$n=4, a={3,1,3,4,2}$が与えられたとしましょう。この時、「街0 -> 街3 -> 街4 -> 街2 -> 街3」と動き、(街3に2回止まったので)ここで動作を止めるという動作になります。
図に示すと以下のように表せます。

下の図に注目します。$3->4->2->..$というループ部分と、このループに入るまでの$0$という"しっぽ"に分かれています。さて、尻尾からループにつながっているノード(図では3です)を"ループの入口"と呼びましょう。
このテレポート問題を考えると、ループの入口は尻尾から入り、ループの終わりから戻ってくるところなので(つまり、2度訪れるノードなので)、まさに求めたい答えのノードとなります。
ここで、クールにループの入口を求めることが必要になります。センパイの提案したフロイドの循環検出法を考えます。説明は他の記事に譲りますが、フロイドの循環検出法を用いることで、$ループの長さ\mu$ と $ループの入口のノード\lambda$を知ることができ、この空間計算量はなんと$O(1)$であり、時間計算量は$O(\lambda+\mu)$なので、最悪$O(N)$程度となります。
フロイドの循環検出法についてはRでフロイドの循環検出法を可視化するが分かりやすいです。
これを実装したコードが以下の通りです。
from typing import List
def findDuplicate(nums: List[int]):
hare = tortoise = 0
# カメは速度1, ウサギは速度2で走る
while True: # ぶつかるまでループ
tortoise = nums[tortoise]
hare = nums[hare]
hare = nums[hare]
if tortoise == hare:
break
m = tortoise
# ウサギを初期位置に戻す
hare = 0
while tortoise != hare: # ぶつかるまでループ
tortoise = nums[tortoise]
hare = nums[hare] # ウサギも速度1
l = hare
u = 0
# ループ内で重なっている位置からウサギだけを動かす
while True: # ぶつかるまでループ
u += 1
hare = nums[hare]
hare = nums[hare]
if tortoise == hare:
break
# m:衝突が発生するまでの階数
# l:、u:ループの長さ
print("debug: m=",m, "l=",l, "u=",u)
return l
print(findDuplicate([1,3,2,4,1,5]))
print(findDuplicate([3,3,4,2,5,1]))
print(findDuplicate([2,2,3,4,5,1]))
print(findDuplicate([4,3,4,2,1]))
# 適当な"30"の重複が存在するランダムな順序のリストを作成
import random
l = list(range(1,100)) + [30]
random.shuffle(l)
print(findDuplicate(l))
実行結果:
debug: m= 4 l= 1 u= 3
1
debug: m= 1 l= 3 u= 5
3
debug: m= 1 l= 2 u= 5
2
debug: m= 2 l= 4 u= 2
4
debug: m= 40 l= 30 u= 17
30
振り返りと実験
ここで、時間計算量と空間計算量を振り返ります。
| アルゴリズム | 時間計算量 | 空間計算量 |
|---|---|---|
| 1:ソート&線形探索 | $O(NlogN)$ | $O(N)$ |
| 2:辞書 | $O(N)$ | $O(N)$ 但し、辞書の実装依存により大きく変化 |
| 2改:リスト | $O(N)$ | $O(N)$ |
| 3:フロイドの循環検出法 | $O(N)$ 定数倍が多め | $O(1)$ |
付録に上げたコードで$N=10^{7}$で重複はランダムに選択したデータに対してそれぞれのアルゴリズムを実行して、時間とメモリを計測しました。
これは、以下のように実験を行いました。
- (gen.pyを使い)$1~10^7$およびその中のランダムな数字を1つだけ加え、シャッフルしファイルに書き込む
- 各アルゴリズムはそのファイルを読み込み、処理を行う(これらを処理1,2,2改, 3と呼ぶ)
- 読み込むだけの処理を行う(これを処理0とよぶ)
- 各アルゴリズムの実行時間・メモリから処理0の実行時間・メモリを引く。これにより、処理にかかった時間・メモリを計算する
以下は、処理1,2,3のメモリ使用量・実行時間から処理0のメモリ使用量を引いたものです。
| 回数 | 1実行時間 | 2実行時間 | 2改実行時間 | 3実行時間 | 1メモリ | 2メモリ | 2改メモリ | 3メモリ |
|---|---|---|---|---|---|---|---|---|
| 1 | 8.7 | 2.3 | 1.2 | 3.1 | 43MB | 491MB | 78MB | 0MB |
| 2 | 8.8 | 1.5 | 0.8 | 3.6 | 43MB | 245MB | 78MB | 0MB |
| 3 | 8.5 | 1.3 | 0.3 | 4.8 | 41MB | 245MB | 78MB | 0MB |
| 4 | 8.5 | 2.1 | 1.1 | 1.5 | 39MB | 491MB | 78MB | 0MB |
| 5 | 9.9 | 1.9 | 1.6 | 8.7 | 39MB | 245MB | 78MB | 0MB |
| 6 | 9.3 | 2.4 | 1.4 | 3.8 | 39MB | 491MB | 78MB | 0MB |
| 7 | 7.9 | 0.1 | 0.0 | 2.5 | 39MB | 30MB | 78MB | 0MB |
| 8 | 8.7 | 2.3 | 0.7 | 4.7 | 39MB | 491MB | 78MB | 0MB |
| 9 | 8.9 | 1.2 | 0.6 | 3.8 | 48MB | 245MB | 78MB | 0MB |
| 10 | 8.5 | 2.1 | 0.8 | 6.6 | 38MB | 491MB | 78MB | 0MB |
ここでいくつか分かることがあります。
- 処理1(ソート/線形探索)は全体的に時間が長い。ソートに(おそらく5,6秒)時間を要していると推察される。メモリの使用量は元データ程度である(ソートのために、同じ長さの配列を生成しているはずである)
- 処理2(辞書)は高速であるが、辞書のためのメモリを多量に使う
- 処理2改(リスト)はさらに高速であり、メモリも処理1の倍で安定している。
- 処理3は中間の速度であるが、この処理でメモリをほぼ使用していない
加えて、処理2では面白いことが観察されています。
- メモリ使用量が
30MBか245MBか491MBのパターンしかない
これは、辞書の実装のためと思われます。。辞書は作成される、あるいは要素が追加される時点ではどのくらいのメモリを確保していいか分からないので、小さなメモリを確保し、管理要素が増えると確保量を増やします。上記では十分な実験ではありませんが、おそらく、管理量がある程度以上になると、倍・倍でメモリを確保しに行っているのでないでしょうか。
C言語による比較
同様のアルゴリズムをC(C++ではないです)で実装して試験しました。
- 処理1 はstdlibのqsortでソートします
- 処理2 は実施しません。無印Cではhashmap相当が存在しないためです
- 処理2改 はintのリストで使用を管理します
- 処理2改bitとして、charではなく、long longのビットで使用を管理します
- 処理3は変わらず実施します。
コードは参考4にあります。
上の表とは処理2はなく、処理2bitが入っています
比較の際は気をつけてください。
| 回数 | 1実行時間 | 2改実行時間 | 2改bit実行時間 | 3実行時間 | 1メモリ | 2改メモリ | 2改bitメモリ | 3メモリ |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.5 | 0.1 | 0.0 | 0.8 | 39MB | 39MB | 1MB | 0MB |
| 2 | 2.3 | 0.3 | 0.0 | 0.3 | 39MB | 39MB | 1MB | 0MB |
| 3 | 2.1 | 0.0 | 0.0 | 0.3 | 39MB | 39MB | 1MB | 0MB |
| 4 | 2.4 | 0.0 | 0.0 | 1.2 | 39MB | 39MB | 1MB | 0MB |
| 5 | 2.3 | 0.2 | 0.0 | 1.3 | 39MB | 39MB | 1MB | 0MB |
| 6 | 2.3 | 0.2 | 0.1 | 1.0 | 39MB | 39MB | 1MB | 0MB |
| 7 | 2.2 | 0.2 | 0.1 | 0.3 | 39MB | 39MB | 1MB | 0MB |
| 8 | 2.7 | 0.2 | 0.1 | 0.3 | 39MB | 39MB | 1MB | 0MB |
| 9 | 2.3 | 0.1 | 0.0 | 1.2 | 39MB | 39MB | 1MB | 0MB |
| 10 | 2.0 | 0.0 | 0.0 | 1.2 | 39MB | 39MB | 1MB | 0MB |
- 処理1は最も遅く、メモリ使用量は安定しています
- 処理2改はintと明示することができたので、Pythonと違い、処理1と同じメモリ使用量で済んでいます。速度もPythonに比べ、極めて速くなっています。(Pythonでは処理1に対して4,5倍の高速化だったものが10-20倍に)
- 処理2改bitは1つの履歴管理をint(32bit)でただ一つものものからlong(64bit)でのビットの管理にしたことで、メモリ使用量は32分の1になっています。また、処理速度も速くなっています。おそらくですが、すべての情報がキャッシュに乗るので、メモリアクセスが高速になったと推定されます。
- -処理3は相変わらず、メモリを全く使用しません。処理1に比べておおよそPythonと同等の2倍程度の処理速度のようです。
CとPythonの比較
時間の単位:sec
| 言語 | 1実行時間 | 2実行時間 | 2改実行時間 | 2改bit実行時間 | 3実行時間 | 1メモリ | 2メモリ | 2改メモリ | 2改bitメモリ | 3メモリ |
|---|---|---|---|---|---|---|---|---|---|---|
| Python | 8.8 | 1.7 | 0.8 | - | 4.2 | 40MB | 347MB | 78MB | - | 0MB |
| C | 2.3 | - | 0.1 | 0.0 | 0.8 | 39MB | - | 39MB | 1MB | 0MB |
おまけ: LeetCodeの問題の場合 XORを利用する
最初に貼ったLeetCodeの問題ではある1つの数字が2つだけ出てきます。このため、
1からNまでのXORを取った値をxとします。xに対して、配列aすべての要素でxorすると今回の解aが求まります。
今、例えばN=4として、$a=[3,1,3,4,2]$が与えられたとします。$x=1 \oplus 2 \oplus 3 \oplus 4$とすると、
$$
a = x \oplus 3 \oplus 1 \oplus 3 \oplus 4 \oplus 2 = 1 \oplus 2 \oplus 3 \oplus 4 \oplus 3 \oplus 1 \oplus 3 \oplus 4 \oplus 2 = 3
$$
のように、ただ一度しかaに存在していない数は消え、二度出現した3だけが残ります。
※任意の整数xに対して$x \oplus x = 0$です
また、1からNまでのXORは次のように$O(N)$で計算することが可能です。(2進数で各ビットごとに1か0を判定してあげればよいです)
// 1からNまでのXORを求めるコード
if( ((N+1) / 2) % 2 == 1 ) { a = 1; } else { a = 0;}
for(int i = 0 ; i < 31 ; i++)
if( ((N / (1<<i) ) % 2 == 1) && ((N % (1<<i) ) % 2 == 0)) a += (1 << i);
フロイドの循環検出法では、テレポートのために配列$a$をメモリに持つ必要がありますが、この解法はそれを要しません。
このため、処理2改bitより高速で処理3より消費メモリがすくなく解くことが出来ます。実行結果を以下に示します。
これを書いている際の環境起因で上記のマシンではなく別のマシンでの実行となります。あくまで各アルゴリズムの比較です
■処理3: フロイドの循環検出法
$ ~/time-1.9/time -f "%M KB,%E sec" ./a.out 3 < in7
39704 KB,0:02.07 sec
■処理2改bit: 入力を配列に入れずにそのまま処理
$ ~/time-1.9/time -f "%M KB,%E sec" ./a.out< in7
1844 KB,0:01.06 sec
■xor
$ ~/time-1.9/time -f "%M KB,%E sec" ./dup4< in7
624 KB,0:00.91 sec
このコードの全文は以下のようになります。
# include <stdio.h>
int main(int argc, char **argv){
unsigned int N, a, x, i;
scanf("%d",&N);
N -= 1;
if( ((N+1) / 2) % 2 == 1 ) { a = 1; } else { a = 0;}
for(i = 0 ; i < 31 ; i++)
if( ((N / (1u << i) ) % 2 == 1) &&
((N % ((1u << i) ) % 2 == 0)) ) a += (1 << i);
for(i = 0 ; i < N+1 ; i++){
scanf("%d",&x);
a ^= x;
}
printf("%d\n", a);
return 0;
}
参考1: ランダムの入力データ作成
import random
import sys
n=int(sys.argv[1])
x = random.randrange(n)+1
l = list(range(1,n+1)) + [x]
random.shuffle(l)
print(n+1)
for i in range(n+1):
print(l[i])
参考2: 各アルゴリズムでの入力データロード部分
import sys
fd = open(sys.argv[1], "r")
q = int(fd.readline())
dat = [0] * q
for i in range(q):
dat[i] = int(fd.readline())
findDuplicate(dat)
参考3:検証で実行した内容
rm out*
for i in {0..9}; do
python3 gen.py 1000000 > in6
echo $i
~/time-1.9/time -f "%M,%E" python3 1.py in6 2>>out6.1.csv
~/time-1.9/time -f "%M,%E" python3 2.py in6 2>>out6.2.csv
~/time-1.9/time -f "%M,%E" python3 3.py in6 2>>out6.3.csv
~/time-1.9/time -f "%M,%E" python3 0.py in6 2>>out6.0.csv
done
for i in {0..9}; do
python3 gen.py 10000000 > in7
echo $i
~/time-1.9/time -f "%M,%E" python3 1.py in7 2>>out7.1.csv
~/time-1.9/time -f "%M,%E" python3 2.py in7 2>>out7.2.csv
~/time-1.9/time -f "%M,%E" python3 3.py in7 2>>out7.3.csv
~/time-1.9/time -f "%M,%E" python3 0.py in7 2>>out7.0.csv
done
for fn in `ls out*csv*`; do
sed -i -e 's/,.:\([0-9][0-9]\)\.\([0-9][0-9]\)/,\1.\2/' $fn
done
参考4: Cの実装
# include <stdio.h>
# include <stdlib.h>
int fcmp(const void * n1, const void * n2)
{
if (*(int *)n1 > *(int *)n2)
{
return 1;
}
else if (*(int *)n1 < *(int *)n2)
{
return -1;
}
else
{
return 0;
}
}
int solve1(int N, int* a){
qsort(a, N + 1, sizeof(int), fcmp);
for(int i = 0; i < N; i++){
if(a[i] == a[i+1]) return a[i];
}
return -1;
}
int solve2(int N, int* a){
int *dict = (int *)calloc(sizeof(int), N + 1);
for(int i = 0; i < N+1; i++){
if (dict[a[i]] == 1){
free(dict);
return a[i];
}
dict[a[i]] = 1;
}
free(dict);
return -1;
}
int solve22(int N, int* a){
int cnt = ((N+1) / 64) + 2;
unsigned long* dict = (unsigned long*)calloc(sizeof(unsigned long ), cnt);
for(int i = 0; i < N+1; i++){
if ( ( (dict[a[i]/64] >> (int)(a[i] % 64) ) & (unsigned long)1 ) == 1){
free(dict);
return a[i];
}
dict[a[i]/64] |= ((unsigned long)1 << (int)(a[i] % 64));
}
free(dict);
return -1;
}
int solve3(int N, int* a){
int tortoise;
int hare;
tortoise = a[0];
hare = a[a[0]];
while (tortoise != hare)
{
tortoise = a[tortoise];
hare = a[a[hare]];
}
hare = 0;
while (tortoise != hare)
{
tortoise = a[tortoise];
hare = a[hare];
}
return hare;
}
int main(int argc, char **argv){
int type=1;
if (argc > 1){
type = atoi(argv[1]);
}
int N;
scanf("%d",&N);
int *a;
a = malloc(sizeof(int) * N +1);
for(int i = 0 ; i < N+1 ; i++){
scanf("%d",&a[i]);
}
switch (type) {
case 1:
printf("algo1\n");
printf("%d\n", solve1(N, a));
break;
case 2:
printf("algo2\n");
printf("%d\n", solve2(N, a));
break;
case 22:
printf("algo22\n");
printf("%d\n", solve22(N, a));
break;
case 3:
printf("algo3\n");
printf("%d\n", solve3(N, a));
break;
case 0:
break;
default:
break;
}
return 0;
}