セグメント木で区間に含まれる最長の文字長を得る

セグメント木は「乗せるものによっていろいろなことができる」と書いてあったので思いついたものを実装した。乗せるものの工夫をしなければいけないと各所に書いてあるが良い例だったので投稿。

実現できること

• 初期化: $O(N)$
• 区間のある文字の最大長取得: $O(logN)$
• 1文字置換: $O(logN)$

想定する問題

以下のような問題に高速に答えたい。

• n文字の文字列sが与えられる。sは１文字目から$s_{1}, s_{2} \dots s_{n} $と表現する。
• 次の5種類 q個のクエリに答えろ。

1. set(i,x) $s_{i}$をxという文字に書き換える。
2. getCount(s,t) $s_{s},s_{s+1}, \dots , s_{t}$ の区間に含まれるaの数を答える。
3. getLongestLen(s,t) $s_{s},s_{s+1}, \dots , s_{t}$ の区間に含まれる連続したaの数の最大値を答える。
4. getLeftLen(s,t) $s_{s},s_{s+1}, \dots , s_{t}$ の区間の左端から連続したaの数を答える
5. getRightLen(s,t) $s_{s},s_{s+1}, \dots , s_{t}$ の区間の右端から連続したaの数を答える

• 制約は$ 1 \leq n \leq 100,000 $, $ 1 \leq q \leq 100,000$くらいを想定(★以下でも通るのか調べていない)
• この記事では説明の簡略化のためにaを各カウントなどの対象としている(実際は<char>という文字に対して上記を操作しろという問題になりそう)

方針

各ノードに以下の情報を乗せるセグメントツリーを実装する。
(char, count, leftLen, rightLen, longestLen, noneCount)

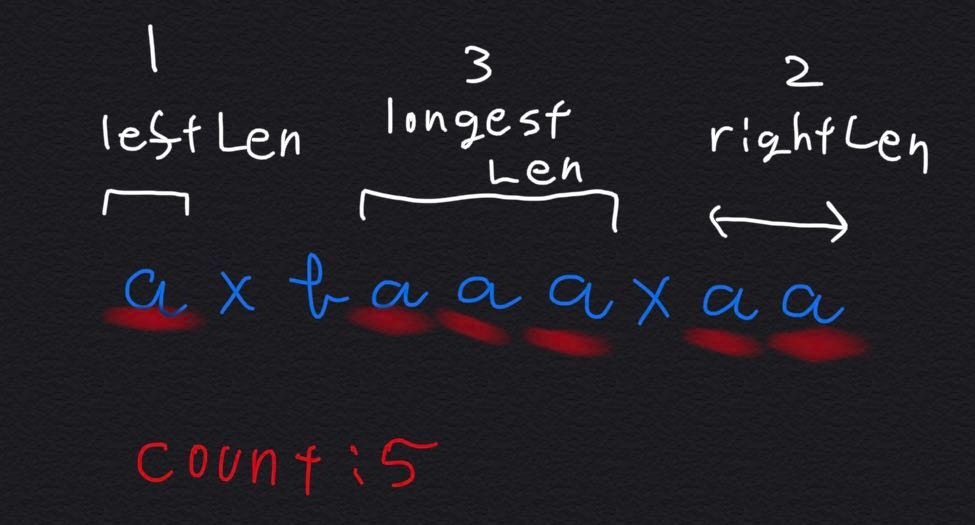
上に例を示す。
char: 入っている文字(図では存在しない)
count: aの数(5)
leftLen: 文字列の左端から連続したaの数(1)
rightLen: 文字列の右端から連続したaの数(2)
longestLen: 区間に含まれる最大のaの長さ（leftLenやrightLenとかななることもありうる）(3)
noneCount: LとRのnoneCountを合算(図では存在しない)
となる。noneCountの必要性は後で説明する。

値の設定 1.set(i,x)　について

高々1文字の値であるため、
- x = aの場合 ("a", 1, 1, 1, 1, 0)
- x = その他の場合(<char>, 0, 0, 0, 0, 0)
であり、セグ木を作る際に埋める右端は(None, 0, 0, 0, 0, 1)とする。

親ノードのupdateの基本

まず、基本的な動作について述べる。以下、L,Rをそのノードの左の子ノード、Rを右の子ノードとする。
(※)についてはいくつかの重要な例外があり、それは後述する。

count: LとRのcountを合算
leftLen: LノードのleftCountを引き継ぐ(※)
rightLen: RノードのrightCountを引き継ぐ(※)
longestLen: 最大値(自身のleftLen, 自身のrightLen, LのrightLen + rのleftLen, Lのlongest, RのLongest)
noneCount: LとRのnoneCountを合算

ここで、longestLenの計算はいくつかの値の最大値となる。まず、LとRそれぞれのlongestLenが候補となることは自明である。LのrightLen + rのleftLenについては親ノードでは、Lの右端とRの左端が連結するため、これらは連続した文字列となり、最長の候補となる。

この後、特別なケース※があると述べたleftLenとrightLenの連続長の処理については以下の2つのパターンを述べる。

基本パターン: 端からの文字列のカウントと2のべき乗長でない文字列の右端の処理

端からの文字列のカウントは特殊で、その配下のノードがすべて連続したaである場合その端はもう片端と合算した連続した文字列を持つ。2つの例を示し、例2がこれに該当する。
- 例1: "aabc" + "aaxz" = "aabcaaxz": 右端からの連続文字列はLと変わらず2、左端も同様に0
- 例2: "aaaa" + "aaxz" = "aaaaaaxz": 左端も同様に0であるが、右端はすべてaであるため、Rの左端と連結されLの文字列長 + Rの左端となる。これが、端からの文字列カウントの基本である。

次に、セグメントツリーの特性上、初期化の際から明らかに生じる問題を図で示す。

セグメントツリーでは基本的に対象とするリストの長さを2のべき乗に揃えて格納する。上記のように"axbaaaa"という7文字を格納すると、右端が空になる。今回はNoneを格納したとする。
この際、ノード6はノード7,8から値を受け取った際、8は値がないため、右側の連続文字列を0として扱おうとする。このため、noneCountを用いる。

• ノード6はノード8から値を受け取った際、この区間長1 - noneCount値1 = 0が含まれているため、rightLenを0 + 2(LのrightLen)として設定する
• ノード2のupdateを考える。同様にRは長さ2 - noneCount1 = 1が含まれているため、leftLenを0 + 2(LのrightLen)として設定する

これを実装したものが以下になる。続く以降の「配慮したケース」のため、右端と左端の両方にnoneCount(パディング分)の処理を入れている。

    def funcSegmentValue(self, lNode, rNode, parentNodeId):
        lchar, lcnt, lconsLeft, lconsRight, lconsLen, lNoneNum= lNode
        rchar, rcnt, rconsLeft, rconsRight, rconsLen, rNoneNum = rNode

        # l, rに含まれる文字の総量
        ncnt = lcnt + rcnt

        # 連結した後の右の長さは原則的に左と一致する
        nconsLeft = lconsLeft
        nconsRight = rconsRight

        # 右のノードを合算するときに右のノードの左端の連続文字列数が足りなくても
        # パディング分と会うなら、左のノードの右端の連続文字列数と合算する
        #print("magic = {0}".format(2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length()))))

        if lconsLeft == (2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())) - lNoneNum):
            nconsLeft += rconsLeft
        if rconsRight == (2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())) - rNoneNum):
            nconsRight += lconsRight


        nconsLen = max(nconsLeft, nconsRight, lconsLen, rconsLen, lconsRight + rconsLeft)

        nNoneNum = lNoneNum + rNoneNum
        res = [nchar, ncnt, nconsLeft, nconsRight, nconsLen, nNoneNum]
        return res

配慮すべきケース: query時の左側の処理

ここで、4文字の"aaab"におけるクエリ$[1,4)$を考える。

"aa"の親ノードは自身は区間[0,1]を担当しているため、区間0,1の子ノード(この場合は葉ノード)に対してクエリを行う。この際、区間0の葉のノードは自身が範囲に含まれていないため、その範囲分(この場合は1)が応答負荷(=None)であると答える。

    def querySub(self, a, b, nodeId, l, r):
        """
        [a,b) 区間の親クエリに対するノードnodeへ[l, r)の探索をデリゲート
        区間については、dataの添え字は0,1,2,3,4としたときに、
        [0,3)なら0,1,2の結果を返す
        Noneとなる条件: r <= a or b <= l
        """
        if (r <= a or b <= l):
            cannotAnswer = (r - l)
            return [None, 0, 0, 0, 0, cannotAnswer]

        if a <= l and r <= b:
            res =  self.dat[nodeId]
            return res

        resLeft = self.querySub(a, b, 2 * nodeId + 1, l, (l + r) // 2)
        resRight = self.querySub(a, b, 2 * nodeId + 2, (l + r) // 2, r)
        res = self.funcSegmentValue(resLeft, resRight, nodeId)
        return res

コード全体

# 対象となる文字の
# 単なる数, 右に連続している個数, 左に連続している個数, 連続している数, (想定では端から)連続するNoneの数
# をカウントします
# cons: consecutive
# dataは
# char=入っているデータ, cnt, consLeft, consRight, consLen, noneNumの数
class segmentTreeCharCount():
    dat = []
    lenTreeList = -1
    targetChar = None
    depthTreeList = 0
    lenPaddingEntry = 0
    unitDefault = [None, 0, 0, 0, 0, 1]

    def __init__(self):
        pass

    def load(self, l, tc):
        self.targetChar = tc
        # len(l)個よりも大きい2の二乗を得る
        self.lenTreeList = 2 ** (len(l) - 1).bit_length()  # len 5 なら 2^3 = 8
        self.depthTreeList = (len(l) - 1).bit_length() # 木の段数(0 origin)
        # lenPaddingEntryは[1,2,3,4,5]を与えたなら[1,2,3,4,5,None,None,None]として扱ったので3を返す
        self.lenPaddingEntry = 2 ** (len(l) - 1).bit_length() - len(l) # 何エントリを補完したか

        self.dat = [self.unitDefault] * (self.lenTreeList * 2)
        # 値のロード
        for i in range(len(l)):
            if l[i] == self.targetChar:
                self.dat[self.lenTreeList - 1 + i] = [l[i], 1, 1, 1, 1, 0]
            else:
                self.dat[self.lenTreeList - 1 + i] = [l[i], 0, 0, 0, 0, 0]
        self.build()

    def funcSegmentValueById(self, nodeId):
        l = self.dat[nodeId * 2 + 1]
        r = self.dat[nodeId * 2 + 2]
        return self.funcSegmentValue(l, r, nodeId)

    # 書く計算をおこなう。
    # この際にはこの計算で境界とするl,r位置であるa,bをいれることで、右端と左端のパディングを行う
    def funcSegmentValue(self, lNode, rNode, parentNodeId):
        #print("funcSegmentValue parentNode={0}".format(parentNodeId))
        #print("L:")
        lchar, lcnt, lconsLeft, lconsRight, lconsLen, lNoneNum= lNode
        #print(lNode)
        #print("R:")
        rchar, rcnt, rconsLeft, rconsRight, rconsLen, rNoneNum = rNode
        #print(rNode)

        # ここは便宜上の名前変更(あまり深い意味はない)
        if lchar is None or rchar is None:
            nchar = None
        elif rchar is not None:
            nchar = rchar
        elif lchar is not None:
            nchar = lchar

        # l, rに含まれる文字の総量
        ncnt = lcnt + rcnt

        # 連結した後の右の長さは原則的に左と一致する
        nconsLeft = lconsLeft
        nconsRight = rconsRight

        """
        #print("searchdepth = {0}".format(self.depthTreeList - ((parentNodeId + 1).bit_length() - 1)))
        if lcnt == 2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())):
            #print("child!L!")
            nconsLeft += rconsLeft
        if rcnt == 2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())):
            #print("child!R!")
            nconsRight += lconsRight
        """

        # ルートの場合、右のノードを合算するときに右のノードの左端の連続文字列数が足りなくても
        # パディング分と会うなら、左のノードの右端の連続文字列数と合算する
        #print("magic = {0}".format(2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length()))))

        if lconsLeft == (2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())) - lNoneNum):
            #print(" parentnodeid {2} l root special cur={0} add={1}".format(nconsRight, rconsLeft, parentNodeId))
            nconsLeft += rconsLeft
        if rconsRight == (2 ** (self.depthTreeList - ((parentNodeId + 1).bit_length())) - rNoneNum):
            #print(" parentnodeid {2} r root special cur={0} add={1}".format(nconsRight, rconsLeft, parentNodeId))
            #print(" nconsRight{0} += lconsLeft{1}".format(nconsRight, lconsLeft))
            nconsRight += lconsRight

        #print("update n={0}, max({1},{2},{3},{4},{5}".format(parentNodeId, nconsLeft, nconsRight, lconsLen, rconsLen, lconsRight + rconsLeft))

        nconsLen = max(nconsLeft, nconsRight, lconsLen, rconsLen, lconsRight + rconsLeft)

        nNoneNum = lNoneNum + rNoneNum
        res = [nchar, ncnt, nconsLeft, nconsRight, nconsLen, nNoneNum]
        #print("Return{0}".format(res))
        return res

    # char=入っているデータ, cnt, consLeft, consRight, consLen
    def build(self):
        for nodeId in range(self.lenTreeList - 2, -1, -1):
            # 重要：このコードはリストを生成しなおすので代入に直すこと！
            self.dat[nodeId] = self.funcSegmentValueById(nodeId)

    def setValue(self, i, a):
        """
        set a to list[i]
        """
        #print("setValue: {0}, {1}".format(i, a))
        nodeId = (self.lenTreeList - 1) + i
        #print(" first nodeId: {0}".format(nodeId))
        """
        self.dat[nodeId] = a
        if a == self.targetChar:
            self.dat[self.lenTreeList - 1 + i] = [a, 1, 1, 1, 1, 0]
        else:
            self.dat[self.lenTreeList - 1 + i] = [a, 0, 0, 0, 0, 0]
        """
        #print("before")
        #print(self.dat[nodeId])
        self.dat[nodeId] = a
        if a == self.targetChar:
            self.dat[nodeId] = [a, 1, 1, 1, 1, 0]
        else:
            self.dat[nodeId] = [a, 0, 0, 0, 0, 0]
        #print("after")
        #print(self.dat[nodeId])


        while nodeId != 0:
            nodeId = (nodeId - 1) // 2
            #print(" next nodeId: {0}".format(nodeId))
            # sum : self.dat[nodeId] = self.dat[nodeId * 2 + 1] + self.dat[nodeId * 2 + 2]
            self.dat[nodeId] = self.funcSegmentValueById(nodeId)

    def querySub(self, a, b, nodeId, l, r):
        """
        [a,b) 区間の親クエリに対するノードnodeへ[l, r)の探索をデリゲート
        区間については、dataの添え字は0,1,2,3,4としたときに、
        [0,3)なら0,1,2の結果を返す
        Noneとなる条件: r <= a or b <= l
        """
        #print("querySub: a={0}, b={1}, nodeId={2}, l={3}, r={4}".format(a, b, nodeId, l, r))

        if (r <= a or b <= l):
            cannotAnswer = (r - l)
            #print(" > None") # これは答えられない数を返すべき
            return [None, 0, 0, 0, 0, cannotAnswer]
        if a <= l and r <= b:
            #print(" > have: {0} [node = {1}]".format(self.dat[nodeId], nodeId))
            #print(" >     : a={0} <= l={1} and r{2} <= b{3}".format(a,l,r,b))
            res =  self.dat[nodeId]
            return res

        #print("querySubcalc: a={0}, b={1}, nodeId={2}, l={3}, r={4}".format(a, b, nodeId, l, r))
        resLeft = self.querySub(a, b, 2 * nodeId + 1, l, (l + r) // 2)
        resRight = self.querySub(a, b, 2 * nodeId + 2, (l + r) // 2, r)
        #print("querySubend: a={0}, b={1}, nodeId={2}, l={3}, r={4}".format(a, b, nodeId, l, r))
        #print(" > L")
        #print("  node{0}: {1}".format(2 * nodeId + 1, resLeft))
        #print(" > R")
        #print("  node{0}: {1}".format(2 * nodeId + 2, resRight))
        #print(resRight)
        res = self.funcSegmentValue(resLeft, resRight, nodeId)
        #print(" > res")
        #print(res)
        return res

    def query(self, a, b):
        return self.querySub(a, b, 0, 0, self.lenTreeList)

    def debugGetSliceStr(self, a, b):
        """
        元の文字列リストの[a:b]を返す: str
        """
        return "".join(list(map(lambda x: x[0], self.dat[self.lenTreeList - 1 + a:self.lenTreeList - 1 + b])))


from pprint import pprint



def test1(a,b):
    pprint(st.query(a, b))
    pprint(st.debugGetSliceStr(a, b))


l = list("xaazaaa")
l = list("xaaaaa0A")
l = list("abaaabcaaaaxasaaa")
st = segmentTreeCharCount()
st.load(l, "a")
st.build()
#st.setValue(2, "x")
#st.setValue(4, "x")
#print("-----")
#pprint(st.dat)

print("----------------------------")
test1(0,9)
st.setValue(1, "a")
test1(0,9)
st.setValue(0, "x")
st.setValue(1, "x")
st.setValue(2, "x")
st.setValue(3, "x")
st.setValue(8, "x")
test1(0,9)