ABC220-F Distance Sums 2 を rerooting (全方位木DP) で解く

全方位木DPで解いていきます。0-indexedで示します。

題意

• 頂点数Nの木があり、各辺の距離は1です。
• 各頂点から、他の頂点すべてまでの距離の和を求めてください（コストと呼びます）。これをN行で出力してください。

考え方: 根0からだけの計算

適当に根を決めDFSして葉から考えればよいです。まず、問題が各頂点ではなくて頂点0を根とした時だけの場合を考えます。各頂点に$cost, num = 0,1$を持たせましょう。

• cost: その頂点を根とする部分木のコスト
• num: その頂点を根とする部分木に含まれる頂点数

とします。さて、今、子$y = y.cost, y.num$だったとして、親$x = x.cost, x.num$にコストを伝搬することを$op(x, y)$と呼ぶとすると、$op(x, y) = x.cost + y.cost + y.num, x.num + y.num$となります。これは、yに距離が$0, 1,2,2$の子(距離0は自分です)がいたとすると、親に到達したときの距離は$1,2,3,3$になります。つまり、yのy.num個の各頂点への距離が+1になるので、$+x.num$することと同値です。

以下のようなイメージになります。

考え方: rerooting

rerootingしていきます。以下の内容とほぼ同じ内容です。

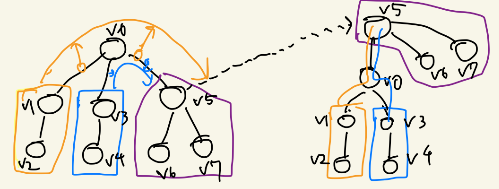
まず、頂点0からのDFSをします。この結果、各頂点は部分木の情報が頂点に持ちます。その頂点の親は、その他すべてのコストを知るため、対象となる頂点の部分木のコストを含まないように、親からコストを渡してやればよいです。

図のように、$v0$からDFSをした後(左図)、$v5$にrerootしたい(右図)とします。この場合、$v0$は$v0$自身の情報を渡すのではなく($v5$の情報を反射してしまうから)、$v1$と$v3$など$v0$からみて$v5$以外のすべての子のコストが$v0$に到着したとして、$v5$に渡してやればよいです。ただし、計算の工夫が必要になります。

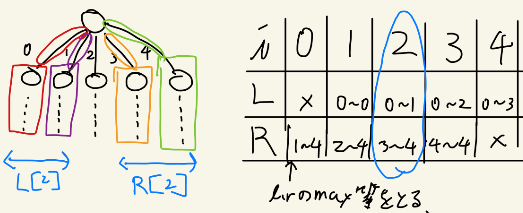
左図のような木で根から2に他のすべてのノードを伝搬させようとすると、子の数$N$としてO(N)の計算が必要になるため、$N$個に情報を伝達させるには$O(N^2)$が必要です。このため、図右のように子iよりも左右の子の情報を基にした情報、$L_i$, $R_i$を累積和のように$O(N)$で計算しておきます。すると、$i$に伝えたい情報を$L$, $R$から$O(1)$で計算できます。この際の集計には$op()$ではなくて親に届く直前までの情報を用いることに注意してください。図右では各子から親の辺を色で囲んでおり、このコストも考慮する必要があります。ただし、$op()$を使う = 親に届ききったときのコストを計算を用いてしまうと、親に届いた際のコスト計算が複数回計上されてしまいます。

実例

図左のようなグラフがあったとします。DFSをすると、根のノードには$9,7$ つまり、根から他のノードへのコストの合計は9であり、根を含む頂点数は9であるという情報が集まります。

図中央は頂点0から子2にrerootしたいとします。頂点0は子1,子3を持つため、それらのコストを合計して($L,R$を用いて)4,3を得ます。自分に届くと、頂点が+1するので、4,4という情報を子2に渡したいです。 これは$op()$で述べたように、コストcostには頂点数numが加算されて伝達されるためです。これより、頂点2は10,7となり、根を2とした時の出力は10とわかります。

図右はさらに頂点2から子6に情報を渡したいと思います。さて、頂点2は親の0から8,4を受け取っていました。そのほか、子である5から1,1を受け取ります。このため、9,5が親と(頂点6以外の)子から集まってくる情報なので、自身の頂点数を足して、9,6を子6に送ります。この際、上記に倣い15,6を送ります。これより、頂点6は15,7となり、根を6とした時の出力は15とわかります。

実装

# include <bits/stdc++.h>
using namespace std;
using ll = long long int;
# define ALL(x) (x).begin(), (x).end()
# define FOR(i, begin, end) for(int i=(begin),i##_end_=(end);i<i##_end_;i++)
# define IFOR(i, begin, end) for(int i=(end)-1,i##_begin_=(begin);i>=i##_begin_;i--)
# define REP(i, n) FOR(i,0,n)
# define IREP(i, n) IFOR(i,0,n)
# define FASTIOpre() cin.tie(0); ios::sync_with_stdio(false); cout << fixed << setprecision(20);


/*
 * この実装は抽象化しているように見せかけて抽象化しきれていない
 * この実装はノードの数やノード自身のコストを数えるのには使えるが、
 * 辺がコストを持つ場合はうまくいかない。(辺にcostを持たせているに使っていない)
 */
template <class S, S (*op)(S, S), S (*e)(), S (*initNodeValue)()> struct rerooting{
public:

    // 辺の持つ情報(make_edgeで辺が持つ情報)
    typedef long long EDGECOSTTYPE;
    struct edge{
        int nextnode;
        EDGECOSTTYPE cost;
    };

    vector<S> dat;
    vector<vector<edge>> G;
    vector<int> parent;
    bool isDFS;
    int n;

    // コンストラクタは頂点の数だけ与える
    rerooting(int n){
        // 全頂点を初期値に設定
        dat = vector<S>(n, initNodeValue());
        G = vector<vector<edge>>(n, vector<edge>());
        this->n = n;
        // -2をUNUSEということにする
        parent = vector<int>(n, -2);
        isDFS = false;
    }

    // 無向辺を張る
    void make_edge(int s, int t, ll w){
        G.at(s).emplace_back(edge{t, w});
        G.at(t).emplace_back(edge{s, w});
    }

    // dfsのヘルパー(rootノードの)
    void dfs(int rootnode) {
        assert(!isDFS); // 2度 DFS NG
        dfsCoroutine(rootnode, -1);
        isDFS = true;
    }
    // DPを行い、葉のノードから親のノードにop()する
    void dfsCoroutine(int curnode, int rootnode){
        parent.at(curnode) = rootnode;
        for(auto x: G.at(curnode)) {
            if (parent.at(x.nextnode) != -2) continue;
            dfsCoroutine(x.nextnode, curnode);
            dat.at(curnode) = op(dat.at(curnode), dat.at(x.nextnode));
        }
    }

    // rerootするためのヘルパー
    void reroot(int rootnode){
        assert(isDFS); // DFSされていないなら実行してはダメ
        // rootnodeからDSFする。この際、rootには零元が送られてきたとみなす。
        // = rootの子(2段目)には、rootの親からの情報などなかったことにする
        rerootCoroutine(rootnode, e());
    }

    // rerooting本体
    void rerootCoroutine(int curnode, S costFromParent){
        // 自分の親を知る
        auto parentNode = parent.at(curnode);

        // まず、ここで自分の子供のコストを保存しておく(参照ではなく値渡し)
        // 値渡ししておかないと、子を更新した後、他の子を更新する際、予期せぬ値になる。
        // datとresをわければ、値渡しは不要になる
        vector<pair<int, S>> childList; // childListはpair で first, second = nextnode, 親からのコスト<S>
        for(auto x: G.at(curnode)) {
            // 親は拾わない。このルーチンの前に伝搬されているから
            if(x.nextnode == parentNode) continue;
            childList.template emplace_back(x.nextnode, dat.at(x.nextnode));
        }

        // rerootingのための累積和的な処理用
        // Nノードの子がいたとして、各ノードにN-1ノード分の情報を伝えようとすると、O(N^2)になる
        // このため、累積和的な考え方をO(N)で事前計算しておき、O(N)で伝搬することでO(N)で伝搬できる。
        // 持たせ方は次の通り
        //    0    1   2   3   4   5
        // L: e   0-0 0-1 0-2 0-3 0-4
        // R:1-5  2-5 3-5 4-5 5-5  e
        // e: 零元(opしても値が変わらない)
        // a-bはaからbのnodeを"+"したもの(opではない)
        int childNum = childList.size();
        //cout << "childnum:" << childNum << "\n";
        vector<S> cumListFromL = vector<S>(childNum, e());
        vector<S> cumListFromR = vector<S>(childNum, e());
        REP(i, childNum - 1){ // childNumまで回す。これが、Nまでじゃないのは、上記のように"x"の場所があるから
            //cout << " rerootCoroutine: cumcalc" << childList[i].first << "\n";
            cumListFromL[i+1]            = cumListFromL[i] + childList[i].second;
            cumListFromR[childNum-1-i-1] = cumListFromR[childNum-1-i] + childList[childNum-1-i].second;
        }

        // 各子のRerootを行う
        REP(i, childNum){ // i番目の子ノードを処理する
            auto childNode = childList[i].first;
            //cout << "curnode:" << curnode << " update childNum: " << childNode << "\n";
            //cout << "L" << cumListFromL[i].cost << "," << cumListFromL[i].nodenum << "\n";
            //cout << "R" << cumListFromR[i].cost << "," << cumListFromR[i].nodenum << "\n";
            // 子に伝搬する情報を作る。まず、渡す情報は、このノードの初期値だとする
            S costToChild = initNodeValue();
            // 子に渡す情報に、親からの情報をopで足す (=親から今のノードにたどり着いた)
            costToChild = op(costToChild, costFromParent);
            // 子に渡す情報に、左側からの情報をopで足す (=左からノードにたどり着いた)
            costToChild = op(costToChild, cumListFromL[i]);
            // 子に渡す情報に、右側からの情報をopで足す (=右からノードにたどり着いた)
            costToChild = op(costToChild, cumListFromR[i]);
            // 子に情報を伝搬する
            dat.at(childNode) = op(dat.at(childNode), costToChild);
            // さらにその子の下を掘る。この際に、このノードに伝えた情報を渡す
            rerootCoroutine(childNode, costToChild);
        }
    }
};


// ノードが持つ情報
struct node{
    ll cost;
    int nodenum;
    // + operatorは必要で、これはrerootの時の累積和に必要
    // opはnodenumを足すが、これは足さない
    node operator+(const node &r){
        return node{cost + r.cost, nodenum + r.nodenum};
    }
};

// ノードの零元。これがないと、rerootの時の累積和ができない
auto e = []{ return node{0, 0}; };

// ノードの初期値。
auto initVal = []{ return node{0, 1}; };

// ノードのマージ演算 xに対してyを足す
auto op = [](node x, node y){
    return node{x.cost + y.cost + y.nodenum, // cost
                x.nodenum + y.nodenum}; // nodenum
};

void abc220_f(void){
    int n; cin >> n;
    rerooting<node, op, e, initVal> rr(n);
    int s, t;
    REP(i, n-1){
        cin >> s >> t;
        s--; t--;
        rr.make_edge(s, t, 1);
    }
    rr.dfs(0);
    rr.reroot(0);
    REP(i, rr.n){
        cout << rr.dat.at(i).cost << "\n";
    }
}


using namespace std;
int main() {
    FASTIOpre();
    abc220_f();
}