Codeforces Round #715 Div. 2C The Sports Festival: 区間DP典型

区間DPの超典型。以下、0-indexed。

この問題の難しさ

入力をソートして、どこからかスタートし、最適に左右にとり続ければよいことがわかるが、これでは、ある地点をスタートして、左右どちらに行くかを計算するため、$O(2000*2^{2000})$のオーダーとなる。

アプローチ

まず、入力をソートしてn個の要素を$a_0, a_1, ..., a_{n-1}$とする。
ある区間$[l, r)$の最善なコストを$dp[l, r)$と表す。この時、求めたい結果は$dp[0, n)$である。ただし、題意より、$dp[x, x+1) = 0$である(つまり、ある１つの数を選んでいるとき)。
この時、$dp[l, r) = min ((a_r - a_l) + dp[l+1, r), dp[l, r+1) + (a_r - a_l))$である。つまり、 ある区間のコストとは、それより1つ短いコストに1つ追加したものである。これを図に示すと以下のようになる。

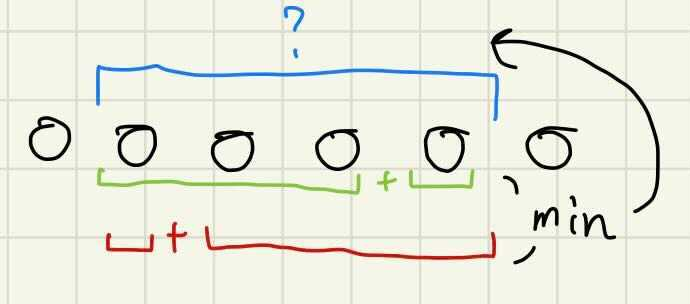
これをテーブルにすると以下のようになる。(線の合流のminをとり、合流地点の$(a_r - a_l)$を足す。

実装上の注意

Pythonは配列へのアクセスが遅い。このため、単純にに書くと(以下実装例のoldFunction)TLEするかぎりぎりになる。これは、Pythonの配列へのアクセスの遅さが関係しているようである。(ある程度大きい配列に対するアクセスのキャッシュの幅が狭いように感じる)
このため、実装例では2本のdpを持ち、下から計算している。

このように

実装(Python3)

import sys
input = sys.stdin.readline
def do():
    n = int(input())
    dat = sorted(list(map(int, input().split())))
    dp = [0] * (n+1)
    for step in range(0, n):
        newdp = [0] * (n + 1)
        for i in range(n-step+1, n+1):
            l, r = n-step-1 , i
            newdp[i] = min(dp[i], newdp[i-1]) + (dat[r-1] - dat[l])
        dp = newdp
    print(dp[n])
do()

def oldFunction():
    n = int(input())
    dat = sorted(list(map(int, input().split())))
    dp = [0] * ( (n+1) * (n+1) )
    for width in range(2, n+1):
        for l in range(0, n - width+1):
            r = l + width
            dp[l*n + r] = (dat[r-1] - dat[l]) + min(dp[l*n + r-1], dp[l*n+n + r])
    print(dp[n])

実装(C++)

using namespace std;
int main() {
    //FASTIOpre();
    ll n; cin >> n;
    ll x; vector<ll> dat(n); REP(i, n){cin >> x; dat.at(i) = x;}
    vector<vector<ll>> table(n+1, vector<ll>(n+1, 1e18));
    sort(ALL(dat));
    REP(i, n) table.at(i).at(i+1) = 0L;
    ll r;
    FOR(width, 2, n+1){
        REP(l, n- width+1){
            r = l + width;
            table.at(l).at(r) = min(table.at(l).at(r), table.at(l).at(r-1) + (dat.at(r-1) - dat.at(l)));
            table.at(l).at(r) = min(table.at(l).at(r), (dat.at(r-1) - dat.at(l)) + table.at(l+1).at(r));
        }
    }
    cout << table.at(0).at(n) << "\n";
}