AtCoder ABC245 F - Endless Walk を 強連結成分分解 + トポロジカルソートで解く

本記事では:

• 問題文中のいくらでも移動を繰り返すことができる頂点を条件を満たすと呼びます。
• 以下のアプローチでは最初に与えられた点を強連結成分の頂点に縮約して考えていきますが。最初に与えられた頂点たちのことを元の頂点と呼びます。
  • 例えば、頂点1,2,3が強連結成分の頂点aに含まれているとき、元の頂点1は頂点aに含まれています。
  • 特に断りのない頂点は強連結成分分解で縮約後の頂点を指します

補題1: 各強連結成分の頂点と辺をまとめたグラフ

アルゴリズムイントロダクション22.5の図22.9のようなグラフを作ります。この記事中ではGsccと呼びます。

• グラフを強連結成分に分解し、それぞれの内部に含まれる元の頂点と辺を1つの頂点として扱います。(縮約)
• ある縮約された異なる2頂点間の元の頂点をつなぐ辺があった場合、その縮約された頂点間に辺を張ります　
• この時、各頂点は含まれる元の頂点の数を値として持つとします。これを頂点のサイズ、と呼びます
• この成分グラフはDAG(有向非巡回グラフ)である ※同書補題22.13を参照

この時、以下が自明です。

• ある２元の頂点u, vがあり、連結成分の頂点cmpu, cmpvに含まれる点とします。元の頂点$u$から$v$に到達できるならば、cmpuからcmpvには到達可能です。元の頂点uからvに到達できないのであればcmpuからcmpvには到達できません。

考え方

• 1:ある元の頂点uがサイズ2以上の強連結成分に含まれる場合、条件を満たす。
  • 強連結成分の定義から、元の頂点u以外の適当な元の頂点vを選んでずっと$u->v->u->...$と移動をすることができます。
• 2: ある元の頂点uからサイズ2以上の強連結成分の点に移動可能な場合、条件を満たす。
  • そのような連結成分の点aに移動してから、1のように移動を繰り返すことができます
• 3: つまり、Gscc上で考えたとき
  • サイズ2以上の連結成分に含まれる元の頂点たちはすべて条件を満たす
  • サイズ1の頂点はサイズ2以上の頂点に到達可能のとき、元の頂点は条件を満たす
  • サイズ1の頂点はサイズ1の頂点にしか到達できないとき、元の頂点は条件を満たさない
    • 次の移動で必ずほかの連結成分に移動しなければならないが、GsccはDAGであるため、いずれサイズ1で出次0の点に達し、それ以上の移動はできないため、条件を満たせない。

と考えられます。このように、強連結成分分解をした成分グラフGscc上で上記3のサイズ1の頂点にしか移動できないサイズ1の頂点を見つけられれば良さそうです。この数が分かれば全頂点数からその数を引くことで、求めたい答えが求まります。

GsccはDAGであることから以下のようにこれらの点を求めることができます。

• ある頂点iについて、size[i]を頂点iのサイズとして、移動可能な隣接するa個の点$p_1,p_2,..p_a$があったとき、canreach[i] = max(size[i], canreach[p_1], canreach[p_2],... canreach[p_a])とする。これは、頂点iから到達可能な最大の連結成分のサイズである。
• つまり、canrearch[i] = 1であるサイズの連結成分に含まれる点は条件を満たさない。(上記3で示した点である)

イメージ

...と文字で書いていてもわかりにくいので以下のように示します。赤い丸は強連結成分分解。それぞれの数字はサイズで、アルファベットは各連結成分分解の名前とします。

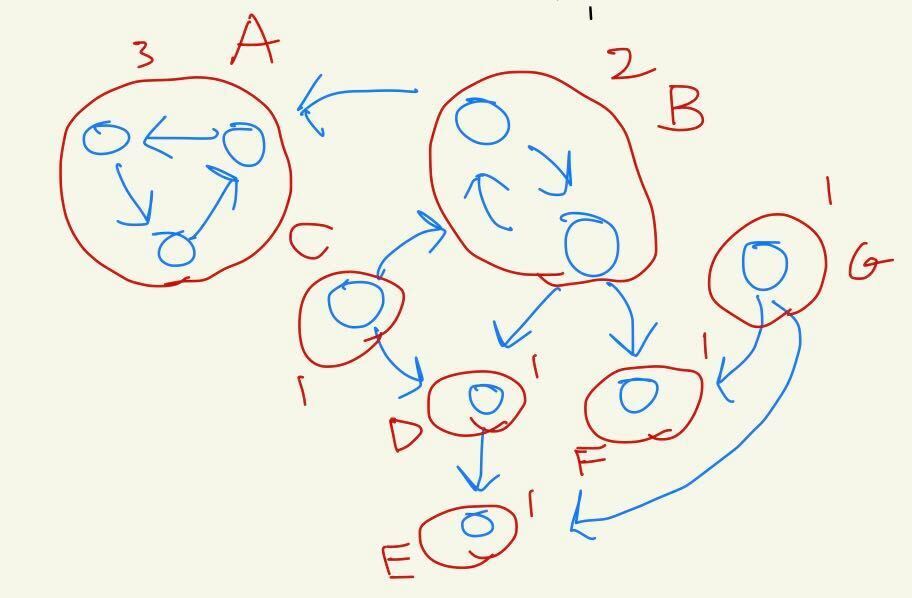
• AやBはその連結成分内で適当に移動し続けられることは明らかです
• E,Fはもともと行き止まりで移動が1回もできないので条件を満たしません。
• DやGも、行き止まりにしか移動できないので条件を満たしません。
• Cはそれ自身の連結成分はサイズ1で、Bに移動すれば条件を満たします。

実装に向けたアプローチ

実装はSTEP1:Gsccを作る と STEP2:Gscc上で条件を満たさない点を求める の大きく２つのパートで構成されます。

STEP1: Gsccを作る

• SCCを行い、各元の頂点に対応する強連結成分を求め、各強連結成分のサイズを記録します。m個の強連結成分が存在したとします。
• m個の頂点を作って、元のグラフの各辺を確認し、異なる頂点間(=強連結成分間)の辺を張ります。この時、すでに接続されている頂点間の辺は不要なので、実装上はsetなどを使えば良いです。これでGsccができます。

STEP2: canrearchを計算していく

各点において、木で子に当たる情報を集約(max)したいので、木で葉にあたる頂点から親をたどります。この時、ある頂点の値を求めたいときは、すべての子の情報が計算済みであれば高速に計算できます。アプローチとしては

• アプローチ1: 葉にあたる出次0の頂点から処理をする。親に情報を渡すと共に、親からその頂点への辺を削除する(出次を-1する)。親にとって、子の処理がすべて終わった(出次=0本)とき、その親を次の処理対象に入れる
• アプローチ2: GsccはDAGであるので、トポロジカルソートを行い、逆に集約していく。トポロジカルソートされた頂点を逆からみれると、子はその親より必ず先に処理をされている。
  • 先に挙げたグラフをトポロジカルソートすると以下のようになります。これを右から見ていけば良いです。(緑の数字は青い矢印の先のcanrearchと自分自身のサイズのmaxです)

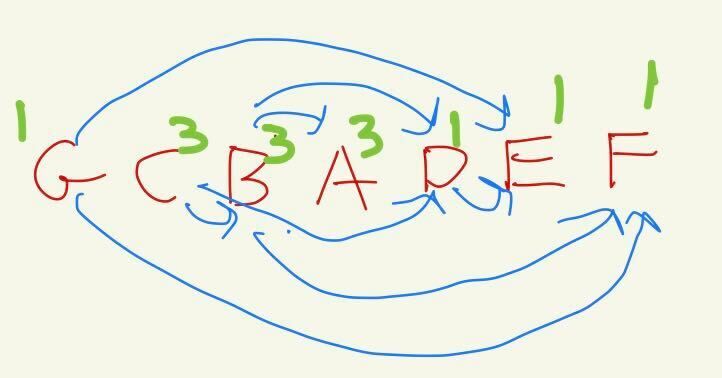
実装する

アプローチ2で解きました

実装(Python)

pythonimport sys
input = sys.stdin.readline
import pypyjit
pypyjit.set_param('max_unroll_recursion=-1')
import sys
sys.setrecursionlimit(2000000)

def main():
    from collections import deque
    class StronglyConnectedComponent():
        def __init__(self, n):
            self.n = n
            self.g = [[] for _ in range(n)]
            self.gr = [[] for _ in range(n)]  # graph rev

        def addEdge(self, u, v):
            self.g[u].append(v)
            self.gr[v].append(u)

        def dfs(self, v):
            # 正方向のDFS
            self.visited[v] = True
            for nxt in self.g[v]:
                if self.visited[nxt]: continue
                self.dfs(nxt)
            self.vs.append(v)

        def solve(self):
            self.vs = []  # かえりがけ
            self.visited = [False] * self.n
            k = 0
            self.cmp = [None] * self.n
            # DFS1

            for i in range(self.n):
                if self.visited[i] is True: continue
                self.dfs(i)

            q = deque([])
            self.visited = [False] * self.n
            for i in self.vs[::-1]:
                if self.visited[i] is True: continue
                q.append(i)
                while len(q) > 0:
                    cur = q.popleft()
                    self.visited[cur] = True
                    self.cmp[cur] = k
                    for nxt in self.gr[cur]:
                        if self.visited[nxt]: continue
                        q.append(nxt)
                k += 1

            return k

    from collections import deque
    class topologicalSort():
        def __init__(self, n):
            self.n = n
            self.g = [[] for _ in range(n)]
            self.edgeNum = [0] * n

        def makeEdge(self, u, v):
            self.g[u].append(v)
            self.edgeNum[v] += 1  # 入次++

        def solve(self):
            q = deque([])
            ans = []
            for i in range(self.n):
                if (self.edgeNum[i] != 0): continue
                q.appendleft(i)
                ans.append(i)
            while (len(q) > 0):
                cur = q.popleft()
                for nxt in self.g[cur]:
                    self.edgeNum[nxt] -= 1
                    if self.edgeNum[nxt] == 0:
                        ans.append(nxt)
                        q.append(nxt)
            return ans


    n, m = map(int,input().split())
    scc = StronglyConnectedComponent(n)
    edges = []

    for _ in range(m):
        u, v = map(int, input().split())
        u -= 1
        v -= 1
        edges.append( (u, v) )


    for u, v in edges:
        scc.addEdge(u, v)
    scc.solve() # 強連結成分分解する
    cmp = scc.cmp # cmp[i] = iの所属する強連結成分の番号
    sccnodes = max(cmp) + 1# 強連結成分の数
    cmpSize = [0] * (sccnodes) # 各強連結成分のサイズ
    for x in cmp: cmpSize[x] += 1 # を計算
    g = [set() for _ in range(sccnodes)] # 強連結成分で表したグラフGscc
    for u, v in edges:
        ucmp = cmp[u]
        vcmp = cmp[v]
        if ucmp == vcmp: continue # 同じ連結成分
        g[ucmp].add(vcmp) # 重複するのでここはsetで記録

    # トポロジカルソートする
    ts = topologicalSort(sccnodes)
    for u in range(sccnodes):
        for v in g[u]: ts.makeEdge(u, v)
    tsres = ts.solve() # これが0...sccnodeの順にトポロジカルソートされている

    canrearch = [0] * sccnodes # 求めるべきcanrearch
    for node in tsres[::-1]: # トポロジカルソートを逆からたどる
        canrearch[node] = cmpSize[node] # まず、自分の連結成分のサイズ
        for childNode in g[node]: # 各子相当のmaxを取る
            canrearch[node] = max(canrearch[node], canrearch[childNode])

    # canrearch == 1の数。(+=1にしているのは定義より、その連結成分のサイズが1なのは自明のため)
    a = 0
    for i in range(sccnodes):
        if canrearch[i] == 1: a += 1
    print(n-a) # 全頂点からcanrearch=1(というのが条件を満たさない)の点を抜いた数
main()

注意

本問題では自己ループ辺が存在しないことに注意します。

• この条件があったとしても大まかな考え方は変わりませんが、自己ループを持つ頂点を特別に扱う必要があります
• 他にそのノードを適当な双方に辺を持つ2ノードに分割するとこの考え方をそのまま適応できます