全方位木DPについて、なんとなく理解する記事です。自分の考え方のトレースなので冗長です。
ちゃんとした説明は他の記事を見てください。
全方位木DPについて書いている多くの記事で言われていますが、全方位木DPという表現よりReRootingという表現の方がしっくりきます。一度理解すると分かりますが、ある根を決めたらそこから掘っていきすべての頂点を根としたときの結果を求めていきます。
全方位木DPの特徴
- 木DPはある頂点を根としたときの何らかの計算を葉から行いますが、その過程ですべての頂点においてその部分木の計算を行っていることと同じです。
- これを利用して、最初に決めた根から順番にDFSで各頂点を辿り、ある頂点に注目したときその部分木以外の部分木の結果をマージすることで、少ない計算量で各頂点を根とみなした結果を求めていきます
- さらに、この計算の過程では、累積和のように全区間に対する事前計算を行うことで、高速にマージを行います。
木DPの説明
これからは以下のような問題を題材にします。
n個の頂点からなるの無向グラフがあり、木である。n-1個の辺が存在し、s,t,wは頂点sと頂点tを結びこのコストはwである。
全てのについて一番遠い距離を求めよ。
以下のように、Leafからコストを足していきながら、頂点でmaxを取ればよいです。
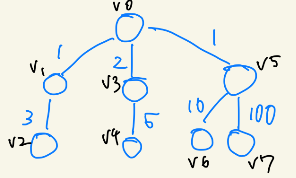
例えば、以下の木があったとします。
このような木があった場合、DFSを行い、頂点の初期コストを0としてから上にたどりながら辺のコストを足していき、各頂点ではそれらのmaxを計算してやればよいです。
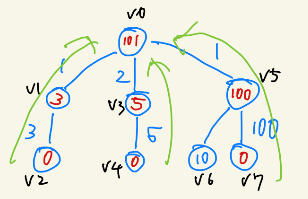
$v_6 \rightarrow v_7$の線が抜けていますが、上記の図のように、$v_2 \rightarrow v_1 \rightarrow v_0$や $v_6 \rightarrow v_5 \rightarrow v_0$のように計算していきます。頂点はそれまでに経由した最大の値を選択して上に伝搬していきます。つまり、以下の図のようになります。
実際のDFS過程ではこのように計算しませんが、上記の図は全方位木DPで大切になる考え方です。$v0$の値というのは、
- $v_1のコストにv1からv0の辺のコストを足したもの$
- $v_3のコストにv3からv0の辺のコストを足したもの$
- $v_5のコストにv5からv0の辺のコストを足したもの$
のmaxを取っていることに他なりません。
また、この時点で、$v0$を根としたときの各頂点の部分木の計算は終わっています。例えば、$v5$は3頂点$v5,v6,v7$の部分木の根としての値が格納されています。
全方位DPをする(誤った解法)
【誤った考え方】
さて、全方位木DPは根からその1つ子をReRoot(根にしていく)というイメージです。次のように考えてみるとどうでしょうか?
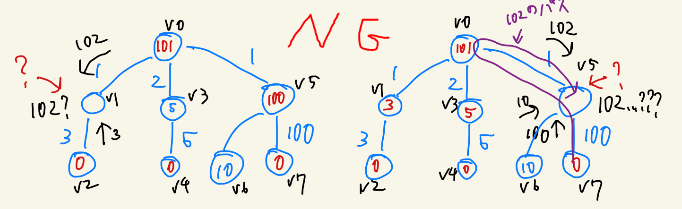
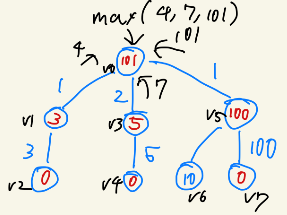
$v_1$を根にしたときの結果を求めたいとします。計算が終わった$v_0$の結果を$v_1$に辺のコストを加えて伝搬させたらどうでしょうか?$v_0$の結果101にコスト1を加えて伝搬させ、maxを取ります。すると、$v_1 = 102$となり、良いように見えます。$v_1 \rightarrow v_0 \rightarrow v_5 \rightarrow v_7$のとき、最大で102です。
ところが、上記右の図のように$v_5$を求めたいと思います。同様に、計算が終わった$v_0$の結果を$v_5$に辺のコストを加えて伝搬させます。$v_5 = 102 $となりますが、これはおかしいです。$v_5$からの最遠の頂点は$v_7$で$100$のはずです。実はこれは$v_7 \rightarrow v_5 \rightarrow v_0 \rightarrow v_5$というように、$v_5 \rightarrow v_0$の辺をダブルカウントしてしまっています。
$v_0$は$v_5$の値を採用した結果なので、この結果を$v_5$に伝搬するのは、反射してしまっている(つまり、本来辿ってはいけない辺を2度辿っている)ことが分かります。
正しく全方位木DPをする
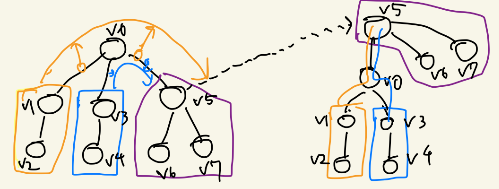
全方位木DPでは以下のように考えます。まず、ある頂点(例えば根$v_0$)にいるとき、その1つ下の子を他の子の結果を使いながら根と見なしていきます。
前提: 今、$v_0$にいます。$v_1,v_3,v_5$が子です。
- ここでは、$v_5$に対してReRootを行います。
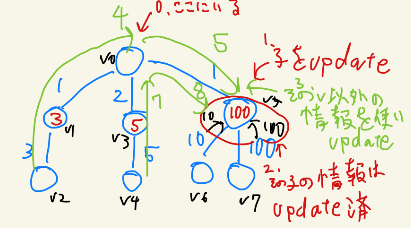
- さて、$v_5$を根と見なした結果とはなんでしょうか?$v_5$は前述の通り、($v_0$を根としたときの)$v_5$の部分木の結果であることは明らかです。図のように、$v_6, v_7$からの情報がupdateされています。
- ここが全方位DPの最も大きなポイントです。$v_0$の情報を加えてupdateしたくなりますが、先に述べた通り、$v_0$は$v_5$の情報に基づく結果であり、これをマージしてはいけません。言い換えると、「$v_0$は$v_1, v_3, v_5$の情報を含むので$v_5$に返してはいけない」のです。それならば、「$v_0$を通過する$v_1, v_3$の情報のみを$v_5$に返せばよい」といえます。この計算は次のように行うことができます。「$v_1$のコストに$v_1$から$v_0$への辺のコストを足したもの(緑の線 コスト4)」「$v_3$のコストに$v_3$から$v_0$への辺のコストを足したもの(緑の線 コスト7)」このそれぞれに$v_0$から$v_5$へのコストを足したもの(このコストは1なので緑の線 コスト5と7になる)を$v_5$に伝搬させればよいです。
やりたいことは、左の図を右の図のようにして$v_5$をRootを見なした(ReRootした)結果を求めたいです。前述の通り、$v_5$は既に部分木である紫のエリアの情報を持ちます。黄色い箱の情報を$v_5$に伝搬することを考えると、$v_1$と$v_0$の辺、および、$v_0$と$v_5$の辺の情報が足りないので、これを足せばよいのです。
つまるところ、ある親の頂点$par$の子が例えば$x,y,z$の3つあったとき、$x$を根と見なしたいのであれば、$par$の$x$以外の子に関する情報(つまり$y,z$)を「必要なコストを加えたうえで」$x$に渡してやればよいです。
計算量に関する工夫
いわば、限定的な区間DPです。
ところで、このReRootのコストは愚直に計算するとに重いです。例えば、以下のようにある親$par$に$node 0,1,2,3,4$がいたとしましょう。
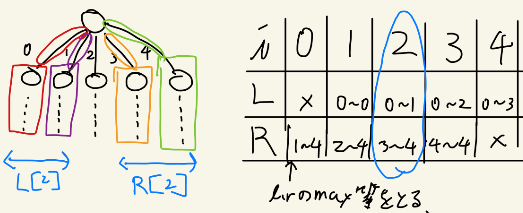
ここで、$node 2$のReRootを行おうとすると、$node 2$は受け取った情報、頂点iまでの情報を$c_i$、自身の情報を$dat 2$、$par$から$node 2$の辺のコストを$e2$とすると、$ max(dat2, c0+e,c1+e,c3+e,c4+e)$としなければなりません。ReRootはすべての頂点に対して行われるため、これでは$O(N^2)$の時間計算量がかかります。
そこで、$par$からのReRootを行う際は、上記の右の図のように累積和のように、左右からのmaxを順番にうまくとったリストを持ちます。例えば、$i=2$のテーブルは$L[2] = max(c0,c1)$であり、$R[2] = max(c3, c4)$です。このテーブルは$O(N)$で計算でき、ルックアップは$O(1)$です。これらに$e$を加えて$node 2$に渡してやればよいです。
このように、ReRootを行う際の各ノードに対しるコスト計算を事前計算することが可能です。 これは、区間DPの特殊な場合とも言えます。
コード
def reroot(n, e):
from collections import deque
# ある頂点を根とした一番近い葉までの距離を計算する
initCost = 999
leafInitCost = 0
op = min
# ある頂点を根とした一番遠い葉までの距離を計算する
initCost = 0
leafInitCost = 0
op = max
dp = [initCost] * n
parent = [-1] * n
dfsRoute = deque([])
# #####################これを入れていいかは問題による
if n == 1:
return [initCost]
# DSFしていく。探索した順に記録。
# 逆にたどることで確実にある頂点の部分木の下の方から訪問できる。
root = 0
q = deque([])
q.appendleft([root, -1, initCost])
while len(q) > 0:
curNode, curparent, curCost = q.popleft()
dfsRoute.append([curNode, curCost])
for nextNode, cost in e[curNode]:
if nextNode == curparent:
continue
parent[nextNode] = curNode
q.appendleft([nextNode, curNode, cost])
# 逆に辿り、コストを計算していく。
# ここで計算したいのは、ある頂点の部分木で最大のコスト
for i in range(len(dfsRoute) - 1, -1, -1):
curNode, curCost = dfsRoute[i]
parNode = parent[curNode]
if parNode == -1:
continue
# これが葉なら
if len(e[curNode]) == 1:
dp[curNode] = leafInitCost
dp[parNode] = op(dp[parNode], dp[curNode] + curCost)
# ここまででDFSの通常の木DPは終わり
# 各頂点の部分木の最大コストがdp
#print("dp", list(enumerate(dp)))
# Rerootしていく。これは根からDSFしていく
q = deque([])
q.append([root, initCost])
res = [initCost] * n
while len(q) > 0:
curNode, costFromParent = q.popleft()
parNode = parent[curNode]
# childListはその頂点の部分木と根のコストの一覧
childList = []
# 今の頂点の隣接を探索していく。ここでのポイントは親側のコストの計算には、
# queueで渡された値を使うこと。
# そうしないと、親のコストは「自分を含む結果」を反射してしまう
# つまり、その頂点 -> 親 -> その頂点を含む
for nextNode, nextCost in e[curNode]:
if nextNode == parNode:
childList.append([costFromParent + nextCost, nextNode])
continue
childList.append([dp[nextNode] + nextCost, nextNode])
# childListは探索順の値が入っている
cl = len(childList)
cumListFromL = [initCost] * cl
cumListFromR = [initCost] * cl
for i in range(cl - 1):
cumListFromL[i+1] = op(cumListFromL[i], childList[i][0])
cumListFromR[cl-1-1-i] = op(cumListFromR[cl-1-i], childList[cl-1-i][0])
res[curNode] = op(cumListFromL[cl-1], childList[cl-1][0])
# 子の探索を行う
for i in range(len(e[curNode])):
nextNode, nextCost = e[curNode][i]
# 親には戻らない
if nextNode == parNode:
continue
q.append([nextNode, op(cumListFromL[i], cumListFromR[i])])
return (res)
def GRL_5_A():
n = int(input())
e = []
for _ in range(n):
e.append([])
# 両方への有向辺とする
for _ in range(n-1):
# node = 0 origin
s,t,w = map(int, input().split())
e[s].append([t, w])
e[t].append([s, w])
res = reroot(n, e)
print(max(res))
def maxDistanceFromEachNode():
n = 13
e = []
for _ in range(n):
e.append([])
# 両方への有向辺とする
def adde(s,t,w):
e[s].append([t, w])
e[t].append([s, w])
adde(0,1,1)
adde(0,6,1)
adde(1,2,100)
adde(1,3,1)
adde(3,4,50)
adde(4,5,1)
adde(6,7,1)
adde(6,8,1)
adde(8,9,1)
adde(8, 10, 1)
adde(10, 11, 1)
adde(11, 12, 1)
reroot(n, e)
# maxDistanceFromEachNode()
GRL_5_A()