LCAを求める際にはオイラーツアーかダブリングを用いる。と述べている記事をよく見かけます。ダブリングの手法について、最初、なぜあのようなコードになるか理解ができなかったので記録としてメモをします。
この記事では次のような問題を解きます。
- 無向な根のある木において、LCAを求めたい。これはたくさんのクエリが与えられる。
- nodeは0-indexedでrootnodeは0
ダブリングについて
過去に書いたSlideShareのAtCoder167Dをダブリングで解くなどを参考にしてください。(他に分かりやすい記事はたくさんあります)
簡単に言えば、(代表されるのは)規則的な遷移のあるグラフにおいて、軽い計算量で事前計算することで、あるノード$x$の$2^k$回目の遷移を$table[k][x]$を参照することで得ることができます。これを用いると任意の回数$a$に対してその経っているビットごとの遷移先を辿ることで高速に($log_{2}x$で)求めることができます。
SlideShareの図の引用になりますが、以下のように計算をします。

ダブリングを用いた根付き木におけるa個先の祖先の求め方
satanicさんの資料がとても分かりやすいです。全ノードにおける1つ先の親を、例えば$ノードx$について、$table[0][x]$とすることで、ダブリングの事前テーブルを計算します。この時、$node0の親は-1$などにしておきます。
※node 0の親は-1など存在しない値にせねばならず、0(自分自身)にしてはダメです。後のLCA判定では親が同じか?という基準で判定を行うため、node 0 の親を0としてしまうと、1つ下のノード$b$と同じ階層に扱われてしまいます。
以下、ノード$x$における$a$個前の祖先を$ancestor(x, a)$とします。
補題: 木におけるノード分辿った後の親ノード
この木のノード数が$numv$の場合、$numv-1$回辿った後の親は必ず$-1$になります。なぜなら、例えば、5個のノードで一番深い場合というのは$0-1-2-3-4$と接続されている場合なので、4回辿ると必ず根に到達します。
LCAの考え方
さて、ここでLCAの特徴を考えます。ここでは、ノード$11と13$のLCA(図では4)を求めたいとします。
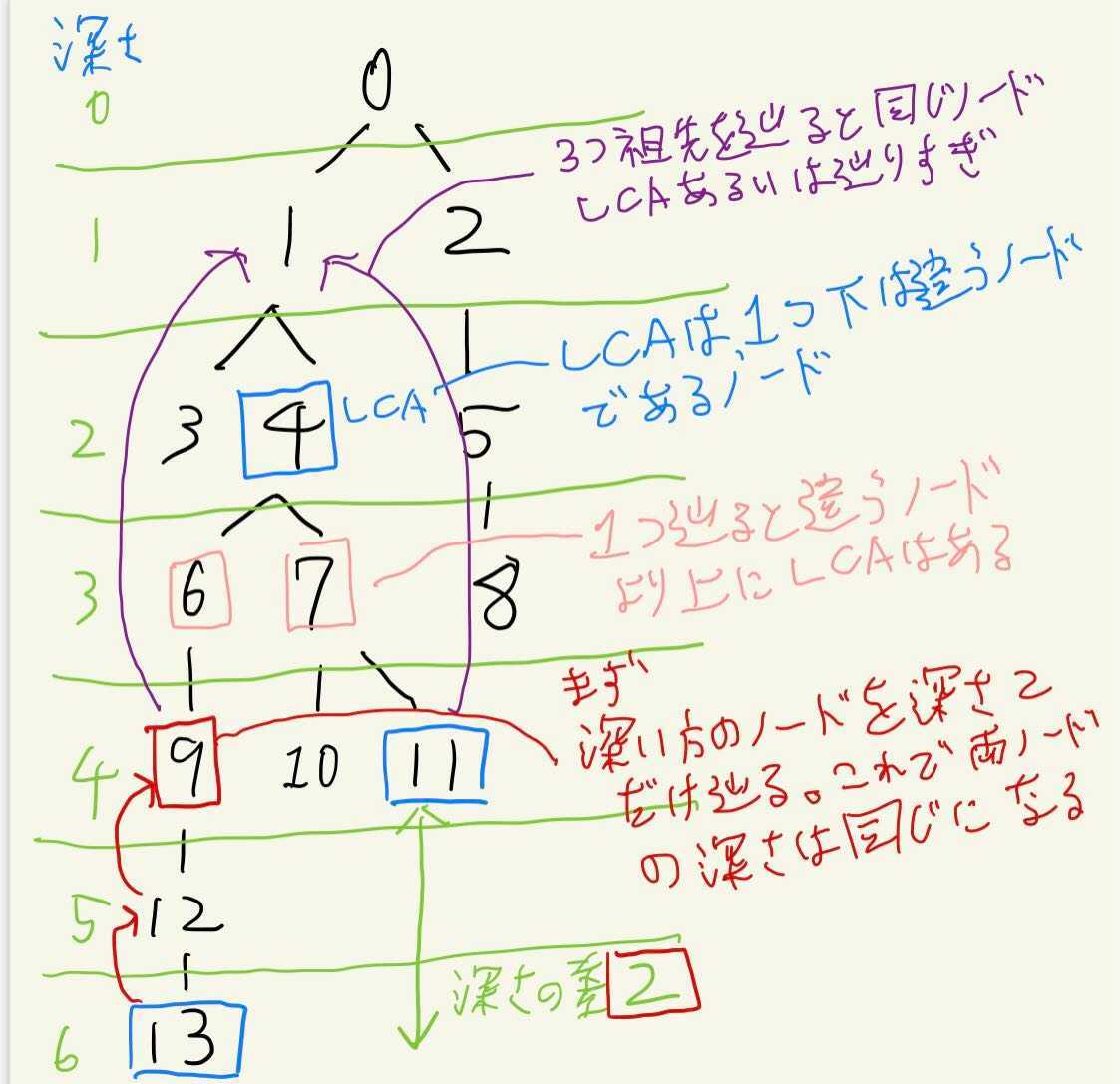
まず、ノードを$u=11, v=13$とします。まず最初に、$uとv$の深さの差を求めます。これは、木の構造を作成する際にDFSなりBFSでたどる際に、distといった変数に入れておけば事前計算可能です。さて、深い方のノードが$u$とするなら深さの差は$dist(u) - dist(v) =2$です。
uを移動して$u = ancestor(u, 2)$のように、深さの差分の分だけ辿ります。これで、$u,v = 9,11$となり、お互いの深さ(dist)が同じになりました。求めるノードの深さを同じにするは、LCAを求める際のポイントです。
深さを合わせることにより以下のようにLCAのノードを定義できます。$i=0,1,2...としていった際に、最初にancestor(u,i) == ancestor(v,i)となる、ancestor(uあるいはv, i)のノードがLCAである$。
また、次のようにも言い換えられます。
$i=0,1,2...としていった際に、最後にancestor(u,i) != ancestor(v,i)であるiに対して、ancestor(uあるいはv, i+1)のノードがLCAである$。
つまり、iを0以上の適当な数としたとき、以下の事が言えます。
-
ancestor(u,i) == ancestor(v,i)であるなら、これがLCAノードであるか(図の水色)、あるいは、辿りすぎており、より下にLCAがある(図の紫)
-
ancestor(u,i) != ancestor(v,i)であるなら、LCAノードはこれより上にある(図のピンク)
LCAを求める考察
木が十分に小さい場合、ある同じ深さのノード$u, v$からスタートして、$u!=v$である限り、$u=ancestor(u,1), v=ancestor(v,1)$してやればよいです。つまり、
while u != v:
u, v =ancestor(u,1), ancestor(v,1)
です。ただし、これでは$O(N)$かかってしまうため、大量のクエリには応えられません。
まず、シンプルな二分探索を考えます。例えば、上記の図のように深さが7であるなら、$l,r = 0,7$のように設定し、lにおいて$u,v$のancestorは異なり、rのとき$u,v$のancestorが同じになるようになるような$l,r$を探してやればよいです。この探索は$O(logN)$で動作しますが、各探索中にダブリングの計算には一定の計算量がかかります。
二分探索の場合$mid=(l+r)//2$としますがここで、深さ$15,7,3,1$を探索すると、ダブリングのテーブルを引く回数は(立っているビットだけの探索で)$4+3+2+1$回、tableを引く計算が起こります。
計算量を落とす工夫
そこで、次のようにancestorの計算をしていきます。まず、最初に、$u,v$の深さを$depth$としたとき、$k$をdepth以上の最も近い2のべき乗2**kの$k$とします。例えば、深さ7であればその数以上の近い2のべき乗は8であるためk=3, 深さ8の場合もk=3, 深さ9の場合はその数以上の2のべき乗は16なのでk=4とします。
この時、 $ancestor(u,2^k) == ancestor(v,2^k)$ です。(深さdepth以上の値なので、ルートノードか-1になります)。このkを用いて、以下のような処理を行います。
for i in range(k, -1, -1): # iをk, k-1, ... , 1, 0で回す
nextu = ancestor(u, 2**i) # = table[i][u]
nextv = ancestor(v, 2**i) # = table[i][v]
if nextu != nextv:
u = nextu
v = nextv
return ancestor(u, 1)
ancestorは、$O(1)$の処理です。これは$table[i][node]$そのものであるからです。
この処理の概要は次の通りです。
- 処理1: iに対して$i=kから0まで$、$2^{i}$の祖先を$u,v$に対して辿る。これを$nextu, nextv$とする。
- 処理2-1: $nextu==nextv$の場合、LCAはもっと手前にあるはずなのだから(あるいはそれがLCAなのだから)、$u,v$はそのままにして、$i -= 1$して処理1に戻る
- 処理2-2: $nextu!=nextv$の場合、LCAはもっと上にあることは明確なのだから、$u,v$を$nextu, nextv$にして、$i-=1$して処理1に戻る
図の例で示すと、
- u,vがそれぞれ、$8,4,2,1$個上に登ってよいかを確かめる。$nextu, nextv$が異なる場合は登ってよく、$nextu, nextv$が同じ場合は登ってはならない。
この処理も二分探索ですが、各確認に必要な計算量は$O(1)$となります。
まとめ
- 木において、ダブリングを用いて$a$個先の祖先を$O(log a)$で求めることができます
- LCAは求めたいu,vの深さを合わせたうえで、ancestorが同じ間辿り続け、ancestorが違うようになるノードがLCAと分かりました
- これは二分探索で行うことが可能ですが、深さが2の階乗でないノードに対して行う場合、さらに計算量を減らすことができます。なぜなら、ある深さ$d$のancestorを求めるには、$d$の立っているbit分のテーブルを引くことが必要になるからです。
- 深さ$depth$ではなくて、深さ$depth$以上の最も近い深さから探索を開始します。これにより、事前計算したダブリングテーブルの行を1行引けばよいです。

