Sparse Tableの最初の理解が難しかったので解説します。Sparse Tableは一度理解してしまえばシンプルなのですが、最初の理解が少し困難にも感じました。この記事は厳密な理解よりなんとなく考え方がわかることを目指します。
以下の記事を参考にしています。
@ageprocpp さんの記事
ikatacosさんの記事
特徴
- 乗せされる演算は結合測があり、冪等性があるものだけです。min, max, gcd, lcmなど。
- 以下の説明では、minとします。
- クエリがO(1)で終わる。
- 以下、各種区間は閉区間で考えます。
基本的な考え方
Table[x]は、1次元の配列を持ち、index0から$2^x$, index1から$2^x+1$のminを取った値を格納していきます。ただし、元の配列の長さを超えるような値は持ちません。
ここでのポイントは、例えば$3,1,4,1,5,9$ があった際に、 $3と1$, $4と1$..というように、重複なく何個かずつ取る操作ではなくて、3と1, 1と4, 4と1 というようにindex0からインクリメントしていき、$2^x$個先までのminを取ります。つまり、$x>0$のとき、各区間は重複します。
この様子を如何に示します。以下、入力は$0-index$のn個の値からなるとし、この配列を$a_0, a_1, ... , a_{n-1}$とします。
図のように$[0]$の時は各値はそれぞれ$0 \leq i \le n$に対して$a_i$です。
$[1]$の時は、$0 \leq i \le n - 2^{1} - 1$に対して、$min(a_i, a_{i+1})$です。
$[2]$の時は、$0 \leq i \le n - 2^{2} - 1$に対して、$min(a_i, a_{i+1}, a_{i+2}, a_{i+3})$です。
...
$[x]$の時は、$0 \leq i \le n - 2^{x} - 1$に対して、$min(a_i, a_{i+1}, ..., a_{2^x-1})$を計算します。
さて、ここで、今回求めたいクエリを$min(l, r) (0 \leq l \leq r < n)$ とします。この時、その区間の長さ$len$は$r-l$となり任意の整数kを考えると、$len = n < 2^{k}$であることは自明です。
kを取りうる最小の整数としたとき、Sparse Tableでは$[0]$から$[k-1]$のテーブルを作ります。例えば、23個の要素がある場合、$23 <= 32 = 2^5$なので[4]までのテーブルを作ります。例えば、8個の要素がある場合、$8 <= 8 = 2^3$なので[2]までのテーブルを作ります。
ここで、min、結合測があり、冪等性があることを利用すると、上記を利用して$O(1)$ですべての区間のminを求めることができます。さて、演算の性質を確認しておきます。$min$を$\oplus$と示すと、$min(a_1, a_2, a_3, a_4) = a_1 \oplus a_2 \oplus a_3 \oplus a_4$
とします。次に、これは、$a_1 \oplus a_2 \oplus a_3 \oplus a_4 = (a_1 \oplus a_2 \oplus a_3 ) \oplus $ (a_2 \oplus a_3 \oplus a_4 )としても示せます。
ここで、$min(l,r$)を求めたいとき、$2^k \leq len$となる最大の整数kを考えます。例えば、長さ6なら、$2^2 \leq 6$なので、$k=2$です。このとき、$[k]$のテーブルを用います。具体的に、$l=1, r=7(閉区間)$を考えます。この時、$[2]$のテーブルの$index1$と$index4$を考えます。これは、$min(a_1,a_2,a_3,a_4)$と$min(a_4,a_5,a_6,a_7)$を示しているので、この両方のminをとることで、$min(a_1,a_2,a_3,a_4,a_5,a_6,a_7)$が求められます。
ここまでを図で示します。
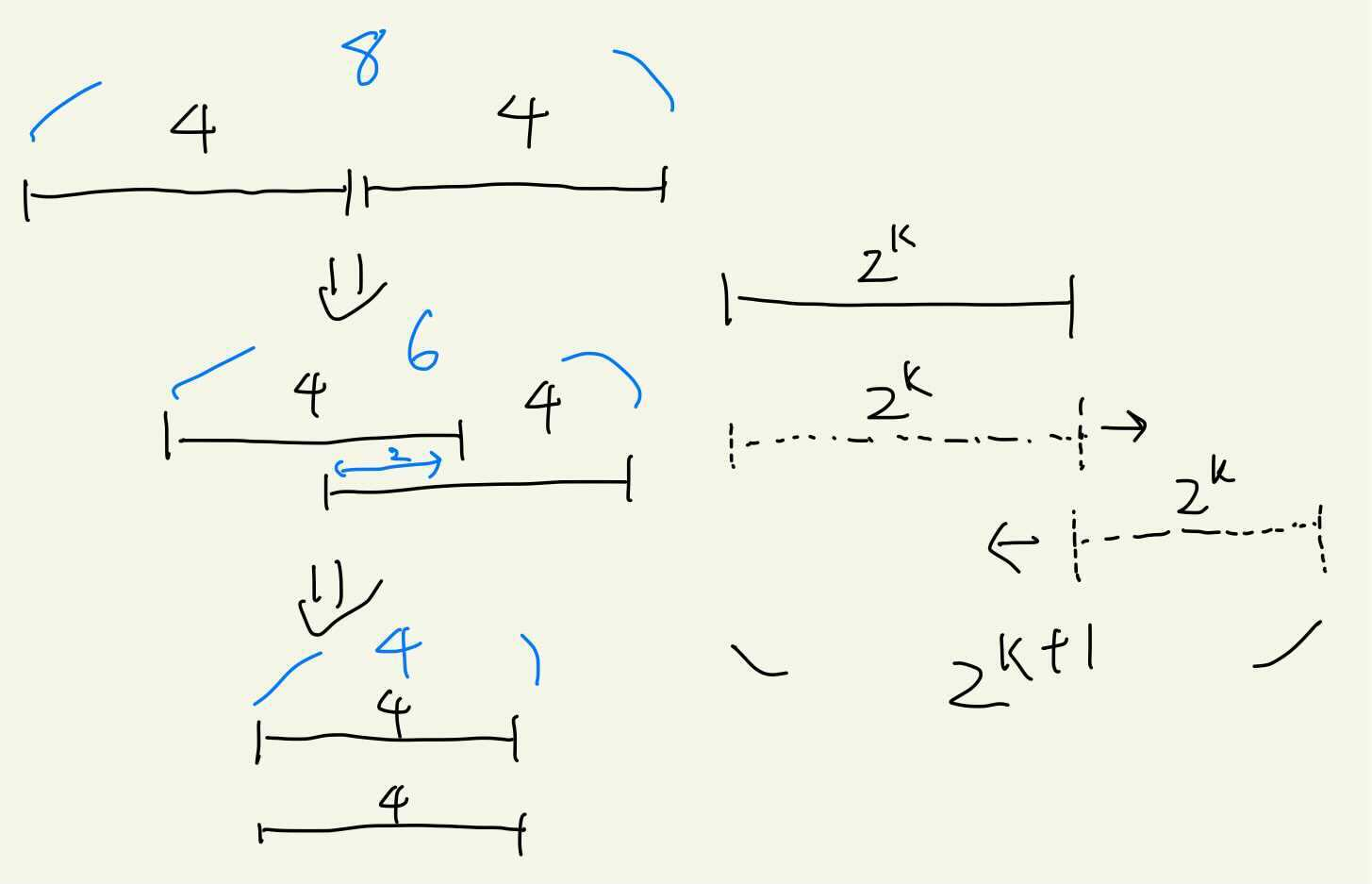図左のように、[2]のテーブルを考えます。[x]のテーブルは、長さ$2^x$の空間のminを持つ棒が２本あるようなもので、最も伸ばせば8の区間を、完全に重ねてしまえば4の区間をカバーできます。逆に言えば、4よりも小さい区間のminは分かりませんし、８よりも長い区間のminを2つの区間だけで求めることもできません。Sparse Tableの大切な考え方は重ねるかつなげることです。ここで、次の図を見ます。
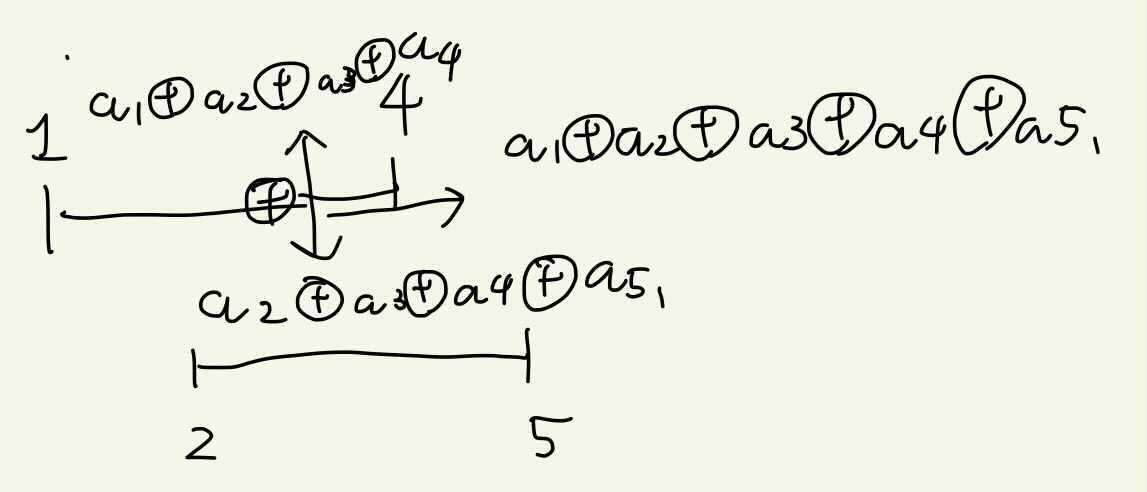
結合測があり、冪等性がある演算であることを念頭に置くと、長さ5の区間を求めたいときは[2]のテーブルを使い図のように考えます。l=1なのですからindex1の[2]のテーブルの値は1から4のminをカバーします。もう一本の棒は、r=5なので、ここに触れるギリギリの線、つまり、$5 - 4 + 1$でindex 2の値を参照します。これはindex 2から5をカバーします。この両者のminをとることで、1から5のminが取れます。
実装
構築を行う際、[x]段目のi番目の要素は[x-1]段目の$i$番目の要素と$i + 2^{x-1}$番目の要素のminをとったものになります。これは最上段の図で言えば、一つ上の同じ色同士のminと同じになります。
クエリは説明で書いた通りです。
class sparseTable(object):
func = None
depthTreeList: int = 0
table = []
def load(self, l):
self.n = len(l)
self.depthTreeList = (self.n - 1).bit_length()
self.table.append(l)
print(l)
for curLevel in range(1, self.depthTreeList):
l = []
for i in range( self.n - (2**curLevel -1) ):
l.append(self.func(self.table[curLevel - 1][i], self.table[curLevel - 1][i + (2**(curLevel - 1)) ] ))
self.table.append(l)
print(l)
def query(self, l, r): # [l, r)
diff = r - l
if diff <= 0:
raise
if diff == 1:
return self.table[0][l]
level = (diff - 1).bit_length() - 1
return self.func(self.table[level][l], self.table[level][r - (2 ** level)])
class sparseTableMax(sparseTable):
func = max
class sparseTableMin(sparseTable):
func = min
import fractions
class sparseTableGcd(sparseTable):
func = lambda self, x, y: fractions.gcd(x,y)
class sparseTableLcm(sparseTable):
func = lambda self, x,y: (x * y) // fractions.gcd(x, y)
l = [3, 1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6]
st = sparseTableMax()
st = sparseTableLcm()
st = sparseTableGcd()
st = sparseTableMin()
st.load(l)
print(st.query(0,1))
print(st.query(0,2))
print(st.query(0,len(l)))
print(st.query(2,3))
print(st.query(2,4))
print(st.query(4,7))