これはSiv3D Advent Calendar 2023 7日目の記事です。
はじめに
今年の6月に「ラムゼーの定理ゲーム」というものを作りまして、少し前にアップデートしました。
https://x.com/spinal_spiral/status/1726907476686381204?s=20
これはどういうゲームかというと、
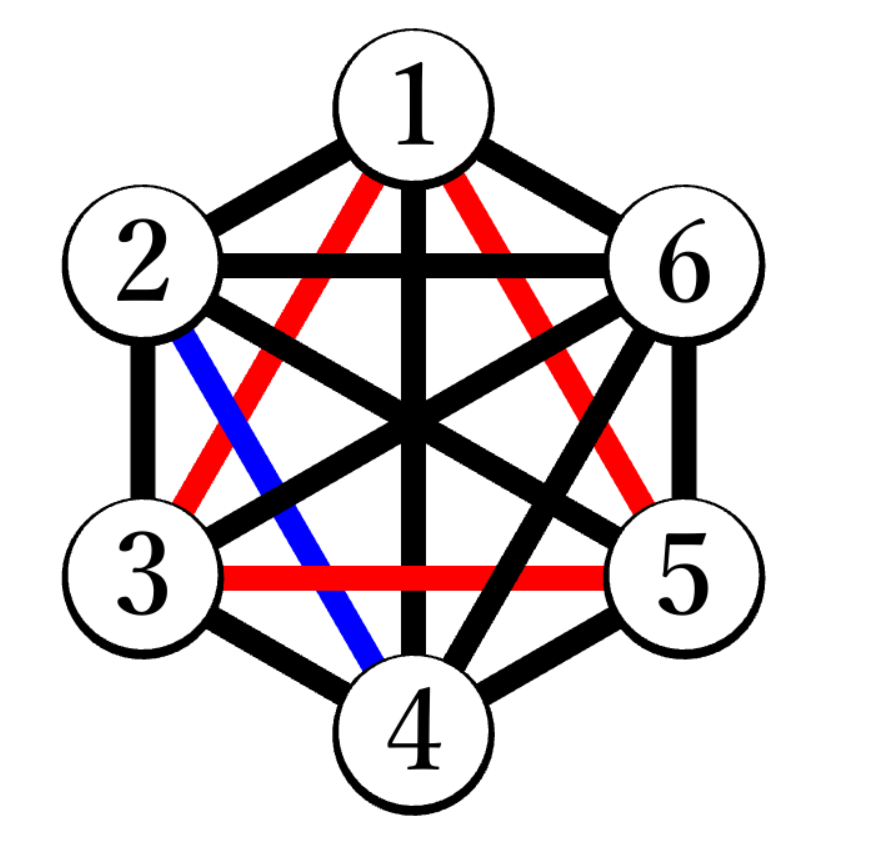
・6頂点の完全グラフの辺を赤か青で塗る
・そのうち3頂点を結ぶ三角形で、3辺が同じ色で塗られたものを作ると負け
というシンプルなゲームです。
1ゲーム3分くらいで終わるのでぜひやってみてください。
1人用モードも2人用モードも用意しています。
作る過程で、いろいろな経験を活かせる機会があったので、裏話的な感じでお話ししようかと思います。
ラムゼーの定理って何?
これを読んでください(丸投げ)
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%A0%E3%82%BC%E3%83%BC%E3%81%AE%E5%AE%9A%E7%90%86
実は私もふわっとした理解しかしていないんです…
このゲームでは、ラムゼーの定理から導かれる、
「6頂点の完全グラフの辺を2色で塗り分けると、そのうち3頂点からなる完全グラフで、すべての辺が同じ色で塗られたものが存在する」
という事実を用いています。
要は引き分けがないということを利用しました。
盤面の管理
盤面は6頂点の完全グラフとなっていて、それぞれの辺を塗り分けていくわけですが、内部で盤面を管理するにあたっては6×6の2次元配列を用いて辺の色だけを記録しています。
頂点はこのゲームにおいては変化しませんからね。
color[i][j] = 頂点 i と頂点 j を結ぶ辺の色を表す。(i<j)
0:黒、1:赤、2:青
という感じです。
各プレイヤーが手を打つたびに3重ループで全三角形を探索して同じ色の辺で結ばれたものがないかどうかを探索します。
3重ループといっても、三角形は 6C3 = 20 個しかないので動作が重くなることはないと判断しました。
コンピュータはどんな方針をとるの?
このゲームには1人プレイモードがあり、その場合コンピュータと戦うことになります。
通常、コンピュータは自滅しない手の中からランダムで選択します。
その手が最善であるかどうかは考慮しません。
というのも、Ver1.0では最善手が分かっておらず、指した手の良し悪しが判断できなかったんですね。
その上、テストプレイでもなかなかいい勝負になっていた(個人の感想です)のでこの仕組みを採ることにしました。
残っている辺すべてについて、赤や青で塗ったときに自滅するかどうか(同じ色の辺でできた三角形ができるかどうか)を調べます。
一番場合の数が多いのは先攻1手目で、辺の数15通り×色数2通り=30通りです。
全探索しても三角形は20通りなので十分高速ですが、辺を1つ決めているということは、負けの原因となりうる三角形の頂点のうち2つを決めているということになるので、3つ目の頂点を残り4つのうちから一つ選んで調べればよいということになります。
そうして自滅しない手の候補を絞り込めたら、それらを配列にまとめてランダムに一つ選びます。
必勝法
Ver2.0では、コンピュータが必勝法を使えるようになりました。
どのように必勝法を見つけているかというと、総当たりです。
ゲーム木の全探索です。
ただ、普通にゲーム中に全探索をしようとすると、盤面の場合の数がそこそこ大きいので時間がかかってしまいます。
各操作の列で考えると、1手目は30通り、2手目は28通り… となるので
30×28×26×…×2 = 42,849,873,690,624,000(通り)
操作の順番が関係ない(途中で勝敗が決まらなければ、操作を入れ替えても盤面と次の手番プレイヤーは同じになる)ことを利用すると、
辺の色だけに注目すればよいので、3^15 = 14,348,907(通り)まで減ります。
でもまだ多いです。ここから盤面遷移の辺を張っていくことを考えると頂点数が10^7あるのはまずいです。
そこで、各状態の到達可能性を考えました。
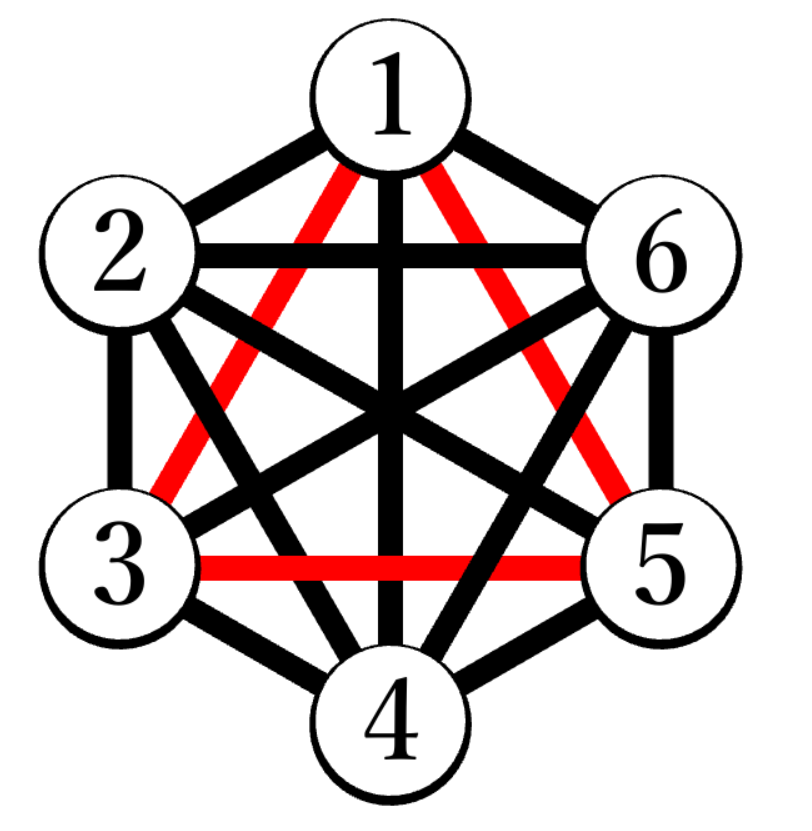
同色辺の三角形ができた時点でゲームは終了するので、例えば以下のような赤と青の三角形が両方できるようなパターンは考えなくてよいです。
また、盤面遷移の辺の結び方を考えます。
この盤面について考えてみます。
ゲームが途中で終了する条件を考えると、下の(a)からは遷移できますが、(b)からは遷移できません。
さらに、同色辺の三角形ができている盤面からは辺を出す必要がありません。
これらを考えると、
状態数:3,731,613
辺数:32,030,880
まで減らすことができました。
また、この状態遷移グラフについては、プレイ中に変化することはない(「状態・盤面」はもちろん変化しますが、「盤面」と「操作」によって「次の盤面」は1通りに決まる)ので、ゲーム木をプレイ中に構成するのではなく、あらかじめファイルにまとめておいてそれを読み込むことにしました。
結局必勝法を使うとどちらが勝つの?
結論から言うと、先攻が勝ちます。
今回はGrundy数というものを使って最善手を取ったときの勝敗の判定を行いました。
ただ、今回に関してはGrundy数が1なのか2なのかにあまり意味がなさそうなので、単純に勝ち負けだけを記録していてもよかったかもしれません。
みんなもコンピュータの必勝法を研究して対人戦で無双しよう!!
なかなかまとまりのない記事になってしまいましたが、ここまで読んでくださりありがとうございました。