AHC030お疲れ様でした。
最終310位でした。サンプルよりも高いスコアを出すまでに相当苦労してしまい、モチベと時間をほぼ使い切ってしまいました。終了後の皆さんの考察を見ていると、もっと頑張れたなぁと思います。いつも思っている気がするな…。
(ABC340とABC341とARC172に勝ててアルゴリズムの方で満足したのもある)
問題
概要
- $N*N$の範囲に、ポリノミノ形状の油田が$M$個ランダムに配置されている。
- 油田の向きと形状は事前に与えられる。
- 油田同士が同じ座標に重なって配置されることもある。
- 同じ形状の油田が複数存在することもある。
- 各マスに存在する油田の個数を、そのマスの「埋蔵量」と定義する。(例えば、同じ座標に異なる油田が$3$つ重なっていれば、そのマスの埋蔵量は$3$)
- 油田の位置を調査するにあたって、以下の3種の行動をとることができる。
- 掘る - $1$か所を指定し、その箇所の埋蔵量がわかる。コスト$+1$。
- 占う - $2$か所以上を指定し、指定した座標の埋蔵量の合計の予想値がわかる。コスト$1/\sqrt{k}$。
本来の埋蔵量の合計が$V$であるとき、予想値$\bar{V}$は、一度に占う対象のマスの数を$k$、事前に与えられるパラメータ$\epsilon$を用いて、以下の平均・分散に従う正規分布からサンプルされた値として得られる。\begin{align} &平均:&&(k-V)\epsilon + V(1-\epsilon), \\ &分散:&&k\epsilon(1-\epsilon) \end{align} - 回答 - $N*N$マス内の油田が埋まっているマスの座標を全て推測する。コスト$+1$。
- 上記の3種の行動を$2*N^2$回まで行うことができる。 回答が不正解の場合でも、行動回数が上限に達するまでは調査を続けることができる。
制約
- $10 \leq N \leq 20 $
- $2 \leq M \leq 20$
- $0.01 \leq \epsilon \leq 0.2$
- 上記の3種の行動は$2*N^2$回まで行うことができる。
- 「回答」が誤っていても、行動回数の上限に達するまで何度でも3種の行動を行うことができる。
目的
できるだけ少ないコストで、回答を成功させる。
やったこと
初期考察
あまりになんもわからん。とりあえず、ぼんやり思ったことは以下の2つ。
- 愚直に全マスを掘った場合、行動回数とコストはともに$2*N^2+1$。これがベースラインになりそう。
- 占いがコストも低くて、有効活用できたらえらそう。
実質何も考えられていないに等しい……。
1日目
サンプルコードを提出(絶対スコア: 12696000000点)
ひとまず正の得点を得る。
ビジュアライザにかけて観察してみると、当たり前ではあるが何もないところをひたすら愚直に掘っているのがもったいない。
油田の形状がポリノミノであるという性質から油田の埋蔵位置はある程度連続しているはずで、そういった無駄な採掘を避けるのが良さそう。
5日目
範囲で占って採掘をスキップ(絶対スコア: 12384051804点)
なんの成果も得られないまま後半戦へ。このあたりでも絶対スコアこそわずかに改善したものの、50ケースの順位スコアでは悪化しています。
サンプルコードのビジュアライズ結果から、最初に一定サイズの長方形領域を占い、ある程度油田がありそうな領域だけ採掘するように変更。
また、これだと占いの分散によって本来油田が存在する範囲に油田がないと誤認する可能性もあるため、一通り回って油田が足りなければ、個別に掘らなかったエリアだけを対象に改めて部分的に占い→ありそうな場所を掘る、を繰り返すようにしました。
「ありそう」の判定については、占い範囲を決めれば平均と分散の値があらかじめわかることを利用し、平均を利用して本来の値を逆算していました。また、分散が大きすぎると埋蔵量の推計値のブレが大きくなりすぎ、特に下振れしたときにそれらがすべて0に丸められてしまうため、精度が落ちてしまいます。そこで、分散が1に収まる程度に占い範囲を押さえました。これで極端なブレを引かない限りは、ある程度占い結果が偏ることを抑えられ、本来油田がある範囲の占い結果が0に丸められることを防げるはずです。
seed=0
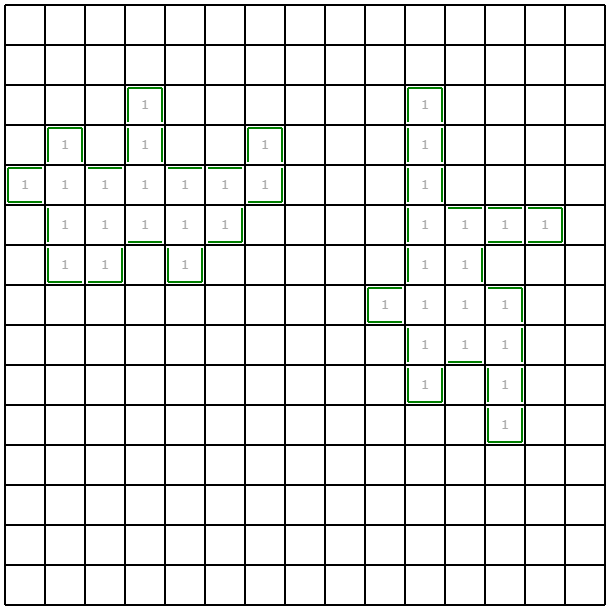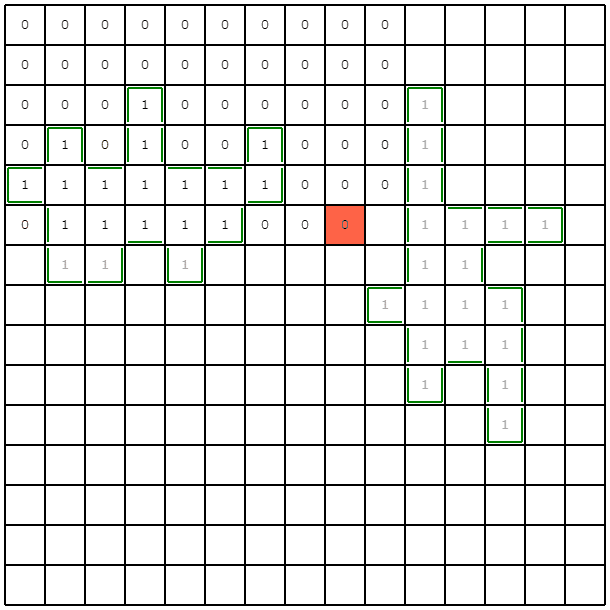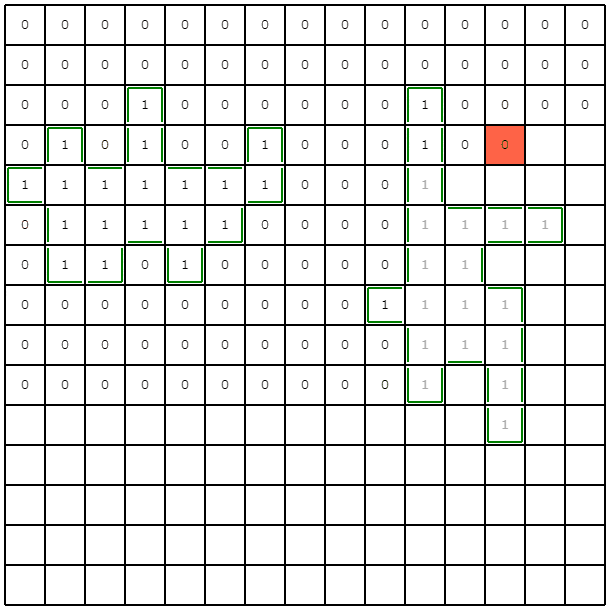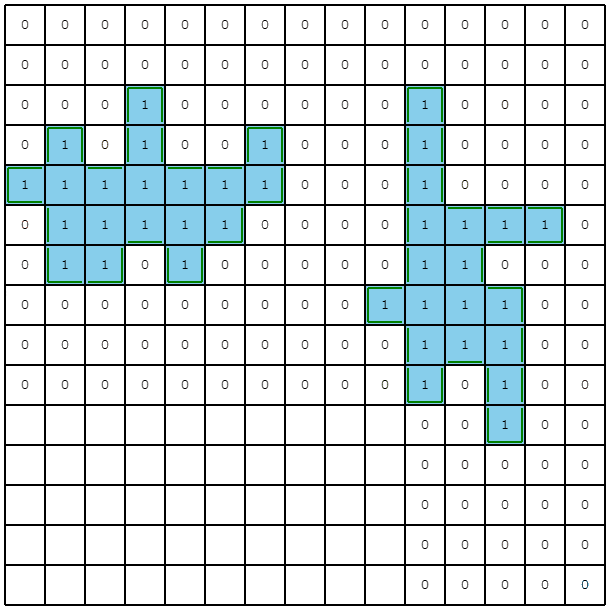
この例だと、左下の領域を1マスずつ掘ることを回避できていて、サンプルより改善できています。
ただ、いくつかの事例ではすべての部分領域に油田があると判定し結局全マスを掘ることになったり、油田があるマスへの占いがすべて外れて何度も重複して占うことになるような事例が多く、改善ケースに比べて悪化ケースの影響が大きく、順位ベースの相対スコアは50ケースの場合にサンプルコードよりも悪化していました。
6日目
ピースの形があらかじめわかっていることを利用する(絶対スコア: 11205965585点)
上記のビジュアライズ結果を見ると、ピースの形状を考慮すると既に盤面が一択になっており、それ以上の占いや採掘が不要な場面があることがわかります。例えばseed=0の例だと、終盤の右下エリアの採掘はほとんど不要です。そこで、盤面全体に対する部分的な占い+採掘が一通り終わった時点で、その時点の確定情報を元にピースを条件に合うように当てはめてみて、もしそのパターンが一択になるようであれば回答として提出するというロジックを組み込みました。
また、完全にすべてのマスの埋蔵量がわかっていなくてもピースの形状から一択しかないというパターンもあります。例えばseed=0の例でいえば、ピースが2種類しかないので、左側の採掘を終えた時点で、左側の埋蔵部分にあてはまるピースは1種類で定まります。すると、右側を掘り始めて出てくる埋蔵エリアにはもう1ピースしか置けません。この形状を考慮すれば、例えば右下の残り1マスについては掘らなくても、理屈上一意に決まりそうです。
seed=0はピースの数が少ないので良いのですが、他のシードだとピースの数が多くて全探索はできません。そこで、埋蔵量が確定していないマスに一定の割合だけはみ出てパターン列挙することを許容することで、全ての採掘を終えていなくても一意に決まるパターンを推測できるようにしました。
例えば、はみだし許容度が0%だと以下のパターンは特定できません。

右下の1マスの埋蔵量が確定していないためです。しかし例えば10%はみ出すことを許容すれば、この1マスの埋蔵量が確定していないことを無視して当てはめることができます。実際、これで推測される置き方以外の置き方はあり得ないので、これを回答として提出することができます。
この方法は多少のスコア改善に寄与しました。
対応後

乱数が変わっているので直接的な比較ができませんが、対応後の場合だとすべてのマスの埋蔵量が確定していない段階でも一意に決まれば回答しているため、内部の未確定マスを見逃したことがスコア改善につながっています。
ただ、この時点でも、サンプルの愚直に全部掘るパターンより悪化している事例が残っていました。
埋蔵マスを見つけたら幅優先探索で埋蔵マスを優先的に確定する(絶対スコア: 7041449896点)
これまでの提出の中で特にスコアの悪いものについて、ビジュアライズ結果を眺めながら、改善できない理由を考えます。その理由は大きく次の3つでした。
1. 埋蔵マスへの占い結果を外し続けて確定できない
1. 同一形状、もしくは類似形状のピースが複数存在し、配置パターンが一意に確定しない
1. 多数のピースが隣接または重なっており、配置パターンが一意に確定しない
1つ目については占い結果に対する採掘条件を調整するなど頑張りどころがありますが、2つ目と3つ目は一意に確定したパターンのみを提出するというアプローチをとる限り、回避ができません。というのも、いずれについても盤面内に配置した特定の2つのピースを入れ替えても成り立つというパターンが存在していたためです。占い結果を外す問題については占いというアプローチをとる限り一定の確率で発生することは避けようがないので、後者への対応を考えました。
特に注目したのは3番目のケースです。2つ目のケースは同一形状の油田を同一視するなどの対策がとれそうですが、2つ目は本質的に正解の配置が一意に決まらないようになっている以上、別の方法で回避したいです。そこで、当たり前のように皆さんがやっていた、幅優先探索で油田の存在位置を確定するアプローチにたどり着きます。
油田形状がポリノミノになっているため、4近傍に対して探索することで、埋蔵していないマスに囲まれる領域を優先的に確定できるのです。
また、埋蔵量の確定マスが増えるたびにピースの配置パターンを計算するようにしたことで、途中で一意に決まるパターンを確定できるようになったこともあり、多くのケースで改善できました。
seed=0

占い領域の最大サイズを制限+小領域の探索をやめる (絶対スコア: 6092189928点)
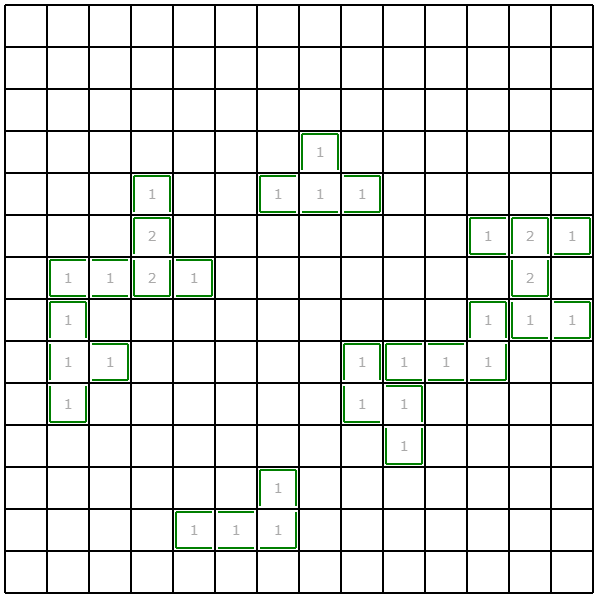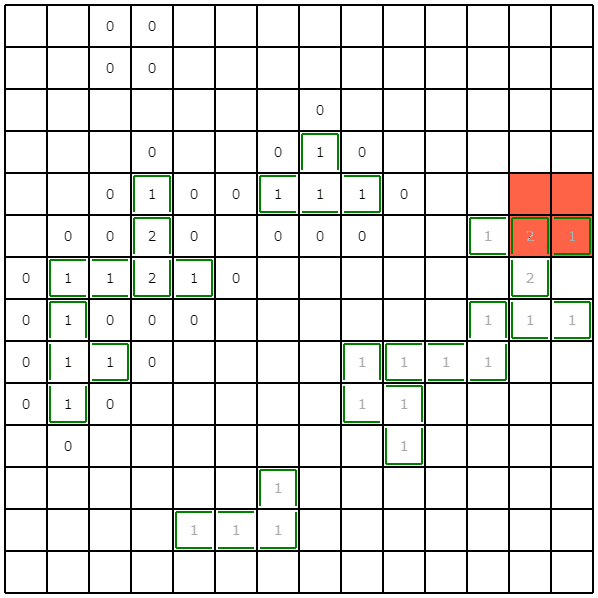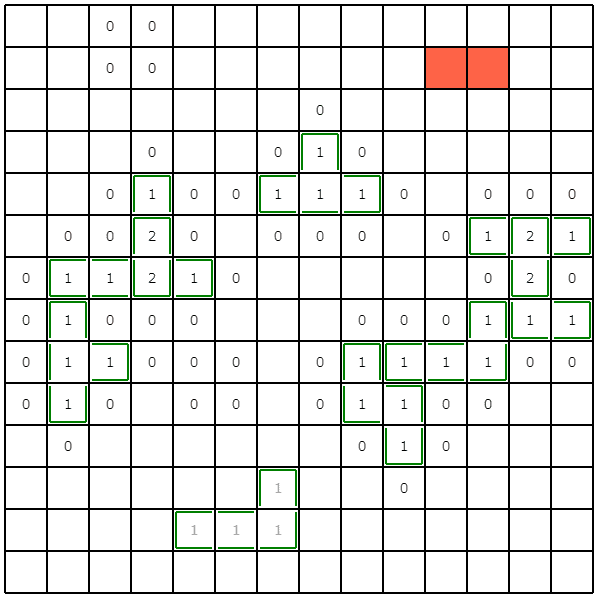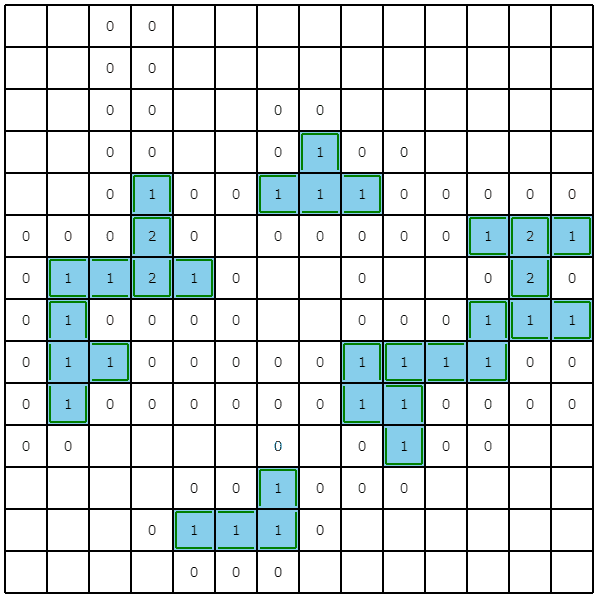
ビジュアライズ結果を眺めていると、幅優先探索後に、3マス以下の小領域がいくつか出てくることに気づきます。今回は制約で、ピースの最小サイズは4マスと与えられているため、3マス以下の領域を探索する必要がありません。そこで、3マス以下の領域は探索・占いをせずに、スキップするようにしました。
また、与えられた$\epsilon$が小さいと占い領域が非常に広くなる事例がありました。今回は1マスでも埋蔵している可能性が占い結果から推測できるなら、領域内を全て掘るという実装にしていたため、あまりに占い領域が広いと、結局全マス掘るのと大差がなくなります。そこで、占い領域の最大サイズを大きくても5*5に絞るようにしました。
これにより、多くのケースで改善が見られました。特にこれまではサンプルの愚直結果を上回るケースが存在していたのですが、この改善によりそういったケースがなくなり、手元の1000ケースですべて下回るようになりました。
seed=0

seed=450
終盤がわかりやすいですが、1マス領域や2マス領域を占わずにスキップしています。
7日目
掘る順番を工夫する(絶対スコア: 5510305991点)
これまでは上のビジュアライズ結果を見てもわかるように、左上から順番に占って、埋蔵量が正っぽければ掘るようにしていました。しかし、ピースの形状があらかじめ与えられているのですから、必ずしもピースが置かれやすい位置が左上だとは限りません。例えば極端な事例ですが、左上に隙間がある十字の形のポリノミノしかない世界なら、一番左上のマスに埋蔵されている確率は0です。確率が0になることはなかなかないでしょうが、偏りは生じえます。特にコーナーケースが意図的に生成されるアルゴリズムとは異なり、ヒューリスティックでは入力の生成方法があらかじめ示されている以上、それに則るのが良いでしょう。今回は入力の生成方法として、ピースをランダムに配置することが明示されていたので、実際にピースをランダムに配置する試行を繰り返し、油田が存在しやすいマスランキングを作るようにしました。
そして、このランキングに従って1マス掘ることを繰り返し、油田を見つけたら幅優先探索で範囲を確定します。この操作で残りの油田形状の候補と盤面上のおける位置の候補が減るので改めてランダム配置を行い、残りの油田がどこにあるかを推定し、そこを掘る……という試行を繰り返しました。これにより、絶対スコアはかなり改善し、提出時点の順位は170位程度まで伸びました。
8日目
掘る順番を工夫する その2(絶対スコア: 5401660505点)
上記提出後、1マス掘りをする前に周辺領域を占って埋蔵量が多そうか確認してから掘るようなことをしていましたが、あまりスコアが伸びません。ビジュアライズ結果を見て悩んでいるうちに、占ってから領域内を掘る際に、端から順に掘るのが非効率ではないかと思いました。
というのは、ポリノミノは4近傍で接する形状になっているので、あるマスに埋蔵されていないとき、その4近傍に埋蔵されている確率は、離れている場所よりも低くなるように思えるからです。もちろん埋蔵確率が低い領域では関係がないですが、今はあらかじめランダムに配置して埋蔵確率が高そうなマスから順に掘っており、かつ事前の占いでも埋蔵されていそうなことを確認してから掘っているわけですから、今掘った位置に埋蔵していないなら、その隣を掘るよりも離れたところを掘るほうが効果的なはずです。そこで、領域内を掘る際に、左上から順番に掘るのではなく、ランダムに掘るように変えました。
これにより、早めに埋蔵位置を見つけられることが増え、スコアが改善しました。
seed=6

既に占った領域の近傍は占わない(絶対スコア: 5341621708点)
ビジュアライザを見ていると、直前に占った領域をすぐに占い直しているような事例があることに気づきました。というのも、最初にピースをランダムに配置して埋蔵されていそうなマスのランキングを用意しているわけですが、当然ながら座標の近いマスのランキングは同じようなものになります。つまり、ランキング順に見ていくと、あるマスAの近傍を占った直後に、マスAの隣接マスであるマスBの近傍を占うといったことが起こるのです。同じ場所を何度も占って確度を高めるより、いろんな場所を占って埋蔵量を確定させる方がうれしいので、近傍は占わないようにしました。これにより多少の改善は見られたものの、頭打ち感がありました。
おわり
結局8日目以降、AHCには取り組む時間を取れず、このままフィニッシュとなりました。暫定290位くらいだったのですが、システムテストで310位までダウン。一応ローカルで1000ケースほどテストケースを用意して、それに対する最良コードを提出していたのですが、周りの方が上手だったようです。
他に取り組めそうだったこととしては、
- 埋蔵マスを見つけた後の幅優先探索の効率化
- 確定情報から油田配置を推定する方法の効率化
などがあります。前者については、残っているピースのパターンを踏まえて選択肢を減らせそうなマスをさがすようなアプローチを考えていたのですが、本番中にはたどり着けず。後者についても、何かしら効率的にパターンを減らせないかなぁと考えていましたが、具体的なアイデアになりませんでした。
終わってみると、上位の方々はこういった考え方を洗練させて取り組まれていたようで、まだまだ手数が足りないなと痛感しました。
本当に情報学研究科修了してるんですか……?
今回のネックになっていた、制約下での油田配置の推定の効率化であったり、ベイズ推定などを用いるアプローチは、発想としてはコンテスト中にぼんやり出てきていたのに実装できなかったものなので、他の方のコードなどを見て復習したいと思います。
今回で水色ギリギリまで来れました。次のAHC031は3月開催だそうです。年度を跨ぐ期間設定なので苦しいですが、やれたらやって入水したいですね。


