この記事について
Aidemyさんの卒業ブログのネタとして素人が時系列分析したものです。
車の運転でいうと、仮免で公道を走っているようなものなので、何かの拍子に本ページにいらっしゃった方は話半分に見て頂ければと思います。
理論等は置いといて、身近なデータでSARIMAモデルで予測をしてみた、、というものです。
分析環境
Google Colab
分析データについて
ThousandeyesでTeams 'https://teams.microsoft.com' のhttpレスポンスを測定し、当該データでSARIMAモデルを構築。(ログ取得方法 )
期間:9/9 ~ 9/19の約10日
測定間隔:1分間隔
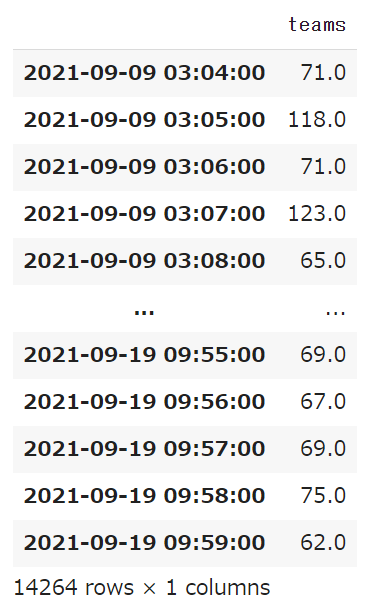
ログは以下の処理を実施し、分析用データとする。
生データをそのまま利用するとGoogle Colabが非常に重くなり、分析が終わらなかったため、30分単位で集約。(おそらく周期性が1400と大きくなったことが原因かと)
df.index = pd.date_range(start="2021-09-09 02:04:00", freq= '1Min', periods=14885)
df = df.dropna()
df_30T = df_d.resample('30T').mean()
可視化によるパラメーター推測
まずはデータを可視化することで、何となくパラメーターを推測してみます。
周期性(s値)
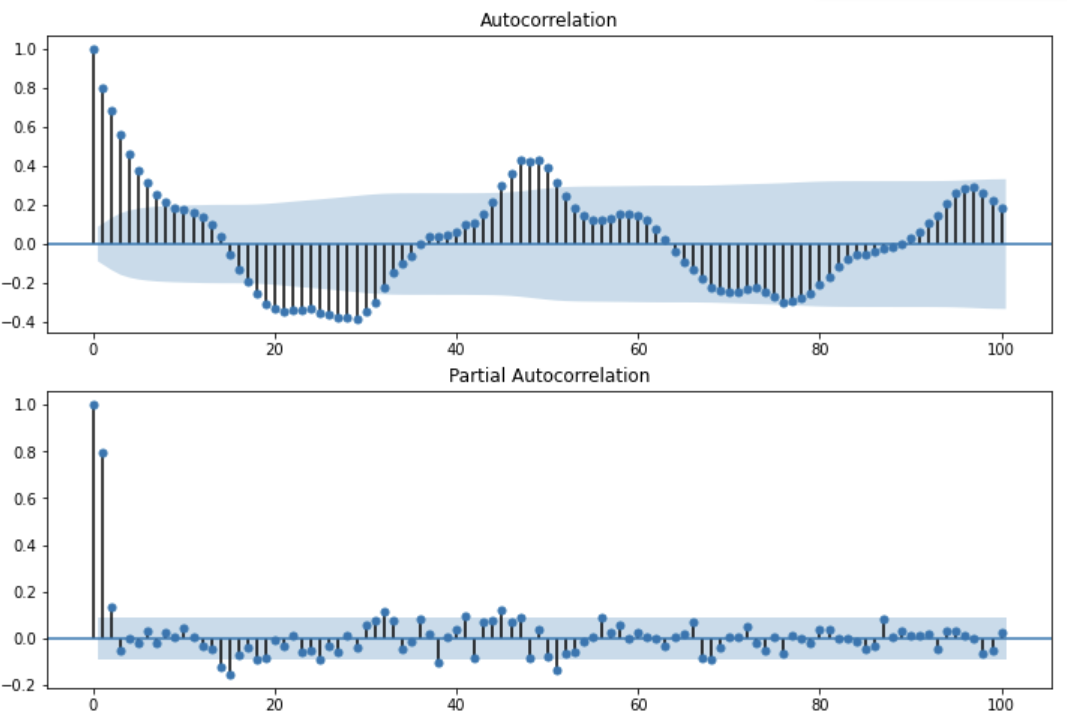
自己相関から概ね48の周期があることが分かりました。30分間隔に集約しているので、単純に24時間周期ですね。。
p値/q値
偏自己相関からは、AR(p)が2 or 3になりそうな事が想定できます。
MA(q)は自己相関から想定できることもあるようですが、、このデータからはちょっと判断つかないですね。
(MA(q)が想定しやすい自己相関では、qを超える周期で急激なカットオフが見えるようです)
import matplotlib.pyplot as plt
import statsmodels.api as sm
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
sm.graphics.tsa.plot_acf(df_30T["teams"], lags=100, ax=ax1)
ax2 = fig.add_subplot(212)
sm.graphics.tsa.plot_pacf(df_30T["teams"], lags=100, ax=ax2)
plt.show()
d値
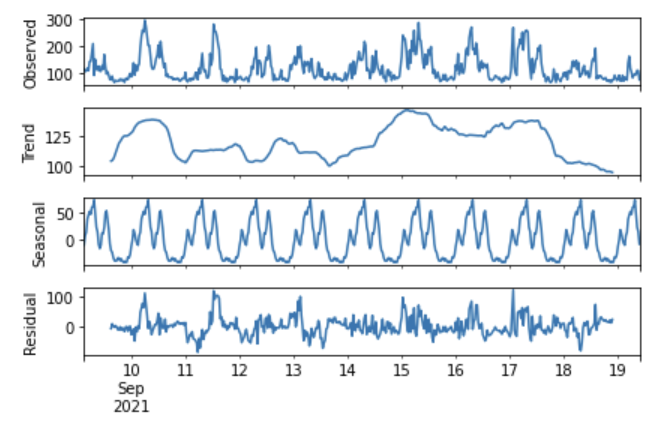
原系列データは以下の通り非定常性になります。
ここではSARIMAのIに当たる部分のd値想定のため、何回差分をとればデータが定常性をもつか?確認してみます。
fig = sm.tsa.seasonal_decompose(df_30T['teams'], freq=48).plot()
plt.show()
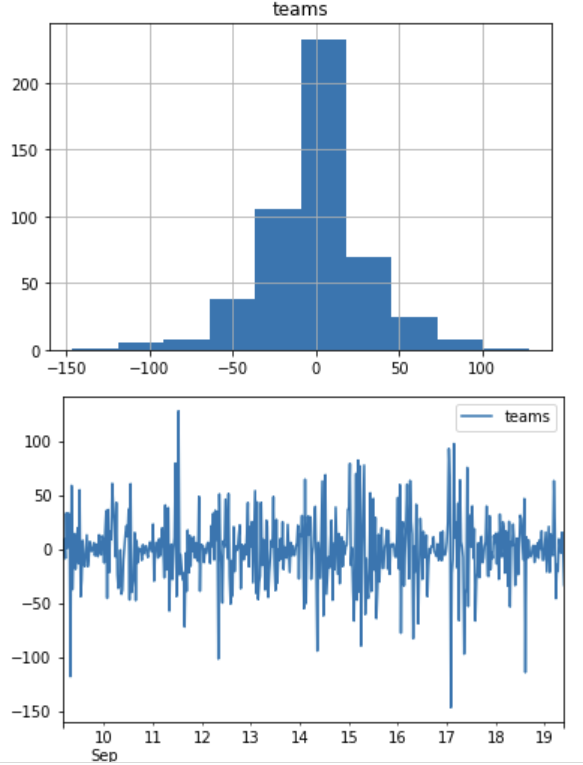
1回差分を取ると以下のようになります。
ヒストグラムは釣鐘型になり、時系列プロットも平均値を中心に変動しているように見えるので、、正確ではないですが、1回差分を取ることで弱定常性を持つと想定されます。
つまりd値が1と想定できました。
df_30T_diff = df_30T.diff()
df_30T_diff = df_30T_diff.dropna()
検定/計算によるパラメーター推測
可視化によるパラメーター推測により設定値に当たりがつけられたので、以下では検定や計算による最適値を確認します。
(同じようなパラメータ推測を可視化や計算で実施しているので、冗長に感じると思います。私もまだ素人なので「こうだ」と言い切れませんが、、検定によるパラメータより、可視化やドメイン知識により想定したパラメータでの分析の方が当てはまりが良いことがあります。今回のデータでもそうだったので、パラメータの推測はいろいろな方法で実施し、一番説明力のあるモデルを検討するのが良いかと思います)
ADF検定
トレンド項なし/定数項ありでP値が有意水準(最低値)になりました。
これにより計算上もd値が1と確認できました。
また解析パラメーターとしてトレンドも含めなくてよさそうです。
# 1回差分
df_30T_diff = df_30T.diff()
df_30T_diff = df_30T_diff.dropna()
res_ctt = sm.tsa.stattools.adfuller(df_30T_diff.teams, regression="ctt") # トレンド項あり(2次)、定数項あり
res_ct = sm.tsa.stattools.adfuller(df_30T_diff.teams, regression="ct") # トレンド項あり(1次)、定数項あり
res_c = sm.tsa.stattools.adfuller(df_30T_diff.teams, regression="c") # トレンド項なし、定数項あり
res_nc = sm.tsa.stattools.adfuller(df_30T_diff.teams, regression="nc") # トレンド項なし、定数項なし
print(res_ctt)
print(res_ct)
print(res_c)
print(res_nc)
# 結果
(-12.216938254044267, 7.265439656096006e-20, 4, 488, {'1%': -4.395029594877641, '5%': -3.844545309330682, '10%': -3.5607819532881466}, 4588.7577776844255)
(-12.228550456539015, 1.67282250245363e-19, 4, 488, {'1%': -3.9774419619548964, '5%': -3.4195250551746343, '10%': -3.132365034855616}, 4586.806047340068)
(-12.240938773011283, 1.0029394404518871e-22, 4, 488, {'1%': -3.4438213751870337, '5%': -2.867480869596464, '10%': -2.5699342544006987}, 4584.81379925971)
(-12.253299279971273, 2.3712332309428833e-22, 4, 488, {'1%': -2.5703367876578875, '5%': -1.941564271274702, '10%': -1.6162869159188984}, 4582.824475630648)
ARMA自動パラメータ推測
上記でトレンドパラメータが"c"と分かったので、以下でARMAのp,q値を推測します。
p=2、q=1でaicが最小となったので、これが最適値のようです。
理論は、、勉強中です。。
sm.tsa.arma_order_select_ic(df_30T['teams'].diff().dropna(), ic='aic', trend='c')
# 結果
{'aic': 0 1 2
0 4799.765552 4776.893909 4778.729730
1 4777.887738 4755.262174 4749.763251
2 4779.560086 4748.691379 4749.500845
3 4778.929904 4749.548725 4750.901277
4 4779.645414 4751.548431 4752.577441, 'aic_min_order': (2, 1)}
SARIMAパラメーターの総当たり検証
以下はAidemyさんのコードそのままです。
上で推測したp,d,q,s値以外のsp,sd,sqを総当たり計算。
ここではbicが最小になるパラメーターが最適値になるようです。。が、
あれ?p値が1、d値が0になっちゃいましたね。
SARIMAではARIMAに周期性の要素が回帰されるので得ることかな。。
ARIMAで推測していた際は(2, 1, 1)だったので、数式は以下になってましたが、
$$Y_t = u + a_1Y_{t-1} + a_2Y_{t-2} + e_t + \theta_1*e_{t-1}$$
SARIMAでは(1, 0, 1), (0, 1, 1, 48)となり、48周期前のデータが回帰されることになるので、AR項の$Y_{t-2}$を回帰するより、48周期前のMA項を回帰させた方が、計算上は適しているという感じでしょうか。
$$Y_t = u + a_1Y_{t-1} + e_t + \theta_1e_{t-1} + \theta_2*e_{t-48}$$
d値に関しては、原系列の1階差より、48周期前の1階差の方が計算上適している、、と言ったところかな。
理屈は何となくわかりますが、、この場合の適切な対処方法はまだわかってないので、今回p値は2で決め打ちしようと思います。
import itertools
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
selectparameter(df_30T['teams'],48)
# 結果
[(1, 0, 1), (0, 1, 1, 48), 4363.500679956852]
SARIMAモデル構築・モデルの妥当性確認
ひとまずまわりました!
が、results画面の解釈が全くできないのでそのまま妥当性を確認します。
mod = sm.tsa.statespace.SARIMAX(df_30T['teams'], order=(2,0,1), seasonal_order=(0,1,1,48))
res = mod.fit(disp=False)
print(res.summary())
# 結果
Statespace Model Results
==========================================================================================
Dep. Variable: teams No. Observations: 494
Model: SARIMAX(2, 0, 1)x(0, 1, 1, 48) Log Likelihood -2169.419
Date: Sat, 25 Sep 2021 AIC 4348.838
Time: 12:09:11 BIC 4369.339
Sample: 09-09-2021 HQIC 4356.921
- 09-19-2021
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.9722 0.174 5.598 0.000 0.632 1.313
ar.L2 -0.0961 0.130 -0.738 0.460 -0.351 0.159
ma.L1 -0.4348 0.161 -2.702 0.007 -0.750 -0.119
ma.S.L48 -0.9995 18.808 -0.053 0.958 -37.862 35.862
sigma2 763.7872 1.43e+04 0.053 0.958 -2.74e+04 2.89e+04
===================================================================================
Ljung-Box (Q): 26.17 Jarque-Bera (JB): 91.31
Prob(Q): 0.96 Prob(JB): 0.00
Heteroskedasticity (H): 1.11 Skew: 0.60
Prob(H) (two-sided): 0.51 Kurtosis: 4.86
===================================================================================
妥当性確認
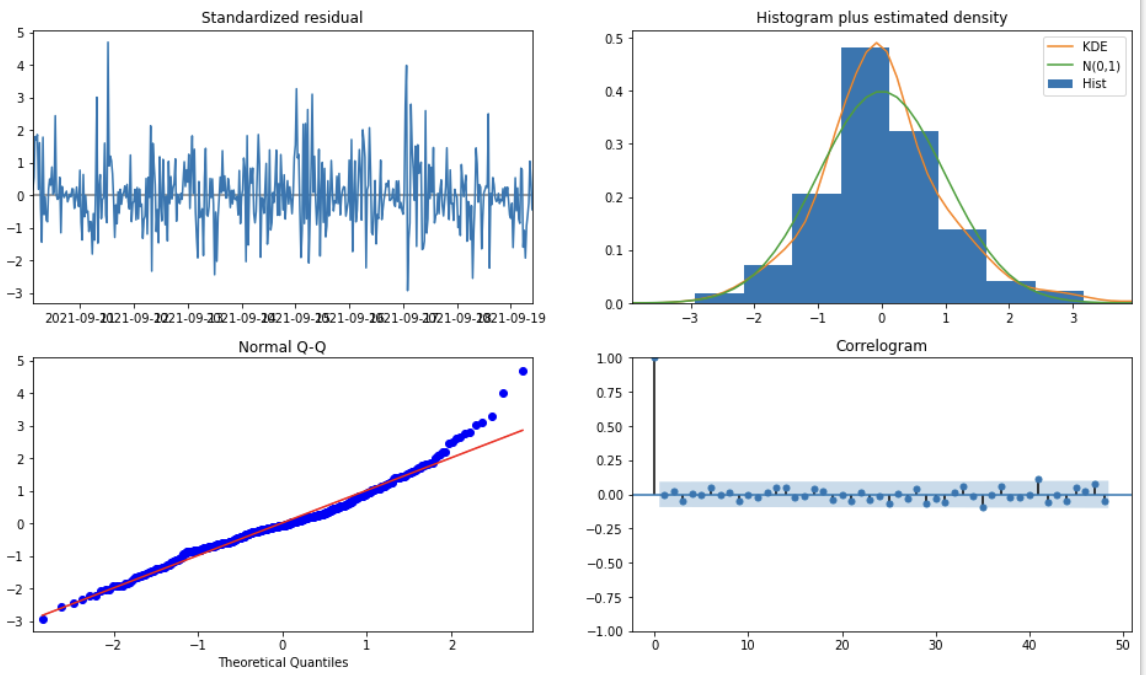
この辺りもまだ勉強中なので正確なところは不明ですが、残差が定常性を持っているか?を確認します。意味合いとしては、分析時点で適切なパラメーター設定ができていれば、残差は定常性を持っているはず。。と言うことになります。
左上はホワイトノイズ??ですかね、、
「時間の経過によらず一定の値を軸に、同程度の幅で振れて変化」しているように見えるので良いかな
右上、、
適切な階差を取ることで、トレンド、周期性を取り除けていれば、KDEが正規分布に従うようです。まぁよいと思われます
左下、、
赤線の沿って青点がプロットされてればよいようです(これはちょっと分かってないです)
右下、、
おかしな相関は見えないのでよいと思われます。ここに相関が残っていると、AR/MA項の設定が適切でないと思われます。
この辺りもAidemyさんの講座では説明されていなかったので、、今後勉強です。。
fig = plt.figure(figsize=(16,9))
res.plot_diagnostics(fig=fig, lags=48)
推測
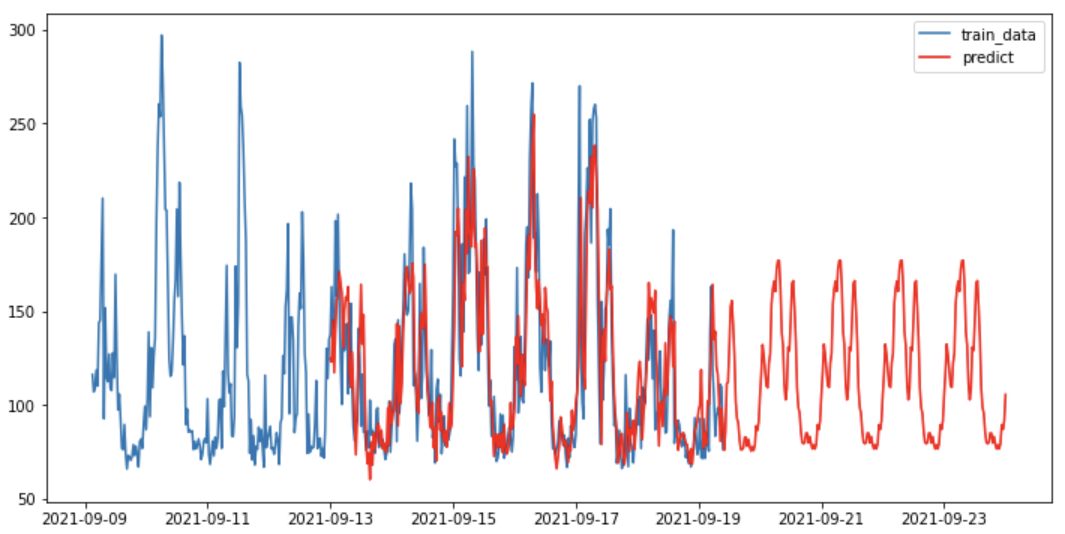
それっぽく推測できたと思いますが、同じ傾向の変動が周期的にでているだけなので、こんなので良いのか疑問はあります。
う~ん、、まだまだビジネスには使えないですね。
sarimax_pred = res.predict('2021-09-13', '2021-09-24')
plt.figure(figsize=(12, 6))
plt.plot(df_30T['teams'], label="train_data")
plt.plot(sarimax_pred, c="r", label="predict")
plt.legend()
plt.show()