なんとなしに、ブートストラップする関数を書いたので、備忘録的にメモを残す。以前、ノンパラメトリック検定について、うんこ記事をかいたので、今回は簡単かつ真面目に書く。
ブートストラップ法
ブートストラップ法とは、手元にあるサンプルを水増しする方法である。手元にデータが100サンプルしかなくとも、「復元抽出」というマジックを使えば10000サンプル分のデータをでっちあげることも夢ではない。そういう技法である。ふざけているわけではなくて、本当にそうである。コードは下記の通り。
def bootstrap_ci(theta, alpha):
lo, hi = alpha * 100, (1 - alpha) * 100
return np.percentile(theta, lo), np.percentile(theta, hi)
def bootstrap(x, B, smooth=False, nss=None):
n = len(x) if nss is None else nss
ssamp = np.random.choice(x, (B, n))
if smooth:
noise = np.random.normal(0.0, 1/len(x), (B, len(x)))
return ssamp + noise
else:
return ssamp
def bootstrap_stat(func, x, B, alpha=.05, smooth=False):
ssamp = bootstrap(x, B, smooth)
theta = np.apply_along_axis(func, 1, ssamp)
bias = np.mean(ssamp - func(x))
ci = bootstrap_ci(ssamp, alpha)
return theta, bias, ci
ちなみに、信頼区間の計算方法には工夫を凝らしたものがいっぱいあるのだが、ここでは普通にパーセンタイルを取っている。
使い方
手元にサンプルが60ある。ヒストグラムは次の通り。
何分布でしょう?正規分布?正解です。いや、まぁ、こういう時は大抵正規分布なので、あてずっぽうでも正解できるが、現実の世界ではそうはいかない。例えばあなたが何かを計測して、ヒストグラムがこれだったら、自信をもって正規分布であると言えるだろうか?(いや、言えやしない、反語)。
そして、もし元の分布が分からないのであれば、平均値は計算出来ても、平均値のばらつきを計算することは通常できない。そこで、ブートストラップ法である。ブートストラップ法を使っても元の分布が何かは分からないことに変わりはないのだが、「手元のサンプルが母集団を代表するとしたらという希望的観測」という魔法により、母集団の平均に対して、サンプル平均がどの程度ばらついているのかを、水増ししたサンプルから計算してしまうことができるのである。素晴らしい。早速やってみる。
boot, bias, ci = bootstrap_stat(np.mean, samp, 10000, 0.05, True)
samp=np.random.normal(2.0,5.0,60)
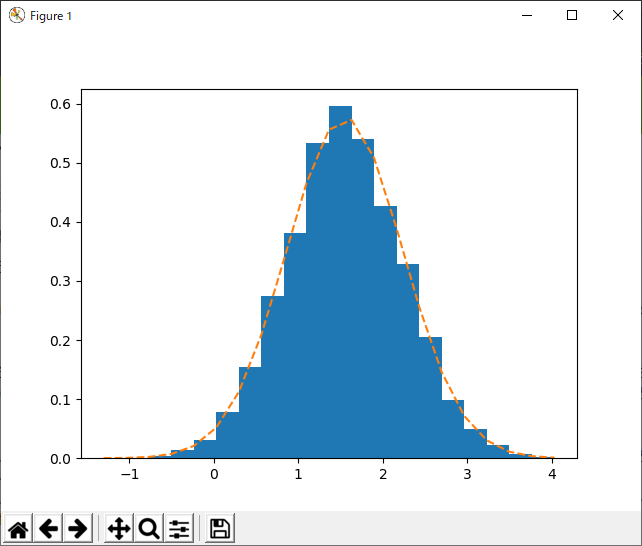
どどーん、見よ、この素晴らしい釣り鐘型の分布を!まさに正規分布(オレンジ色の点線は、このサンプルの平均と分散から推定された正規分布の概形。ばっちり一致している)。これが、あれだね、あの難解な、中心極限定理。あの定理の数値的証明ってやつよ。すげー。
サンプルを水増しするとはどういうことか
というわけで、奇麗な分布が得られたのは嬉しいのだが、実は結構誤差がある。元々の分布の平均は2.0だった。ところが、こいつの平均は下記の通り。
>>> np.mean(boot)
1.5481545437191895
まあ、グラフを見ても、ピークは1.5あたりにある。これはどういうことだろう?推定された平均値が、実は確定値ではなくて、誤差を含む値であったことを思い出すと、すぐに理解できる。上のヒストグラムは、平均値そのものを示しているのではなくて、平均値がどのあたりにありそうか、という誤差を示すグラフだと思えばよい(そして、その誤差は正規分布する)。多少、誤解を受けることを承知で言うと、サンプルから計算された平均の「存在確率」的なものが最も高いのが1.5のところあたり、みたいな話である。だから、「間違い」とは言えない。実際2のところを見ると、結構な頻度でその値を取っていることが分かる。
さて、なぜこんなことになってしまったのか、ということだが、答えは簡単である。元々のサンプル数が少なすぎたのだ。というわけで、見ての通り真の平均は-1から4くらいの結構な幅を持つ正規分布として表現されている。ただ、これは実は元のサンプルの平均値がそもそも偏っているから、こうなっただけであり、ブートストラップ法を使ったせいではない。
>>> np.mean(samp)
1.5537522959540435
何が言いたいのかというと、サンプルの情報量が、ブートストラップ法によって増えるということはないのだ、ということである。さすがに、こんなバカげたことを誤解している人はいないと思うが、100のサンプルから10000くらいのサンプルを作れてしまうので、なんとなく「せいかくに」なっている(情報量が増えている)気がするが、それは幻想である。そうであるがゆえに、ブートストラップ(自分で自分の靴ひもを引き上げる)という呼び方をされる。
じゃあ何がうれしいのさ
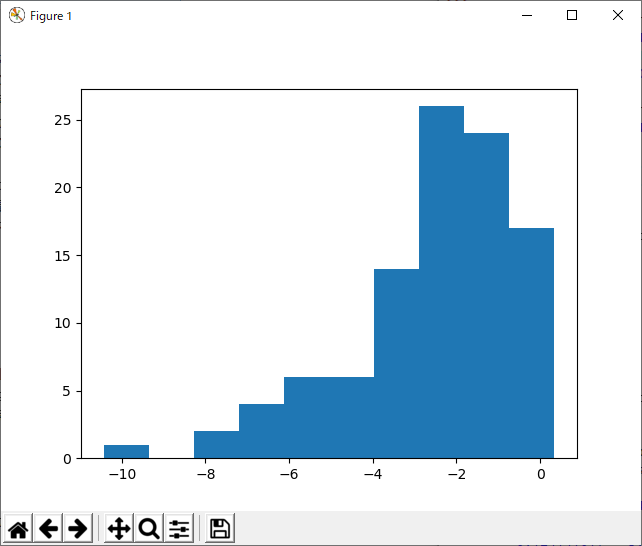
冒頭で述べたように、分布の形が分からないとき、正規分布すると仮定すると結構な間違いを犯すことがある。たとえばこういうの。
これが正規分布でないことはすぐにわかる。なんとなく、左右対称でない分布が良かったので、こんなふうにして作った。
samp=np.log(np.random.normal(0.0,0.5,100)**2);
統計に精通しているあなたなら、この式からちゃちゃっとこの分布(母集団)の性質を把握して、サンプルの平均と分散から信頼区間を計算できるのかもしれないが、私には無理である。それに、今はこういう「データ」をもらったという想定なので分布が何かは、見当がつかないという状況を想定しているのだから(いや、色々ごにょごにょいじったところ、指数を取ってルートしたら正規分布っぽくなったよ、ということもできるけど)、やっぱりよく分からないということにしよう。
そこで、ブートストラップ法を使う。
boot, bias, ci = bootstrap_stat(np.mean, samp, 10000, 0.05, True)
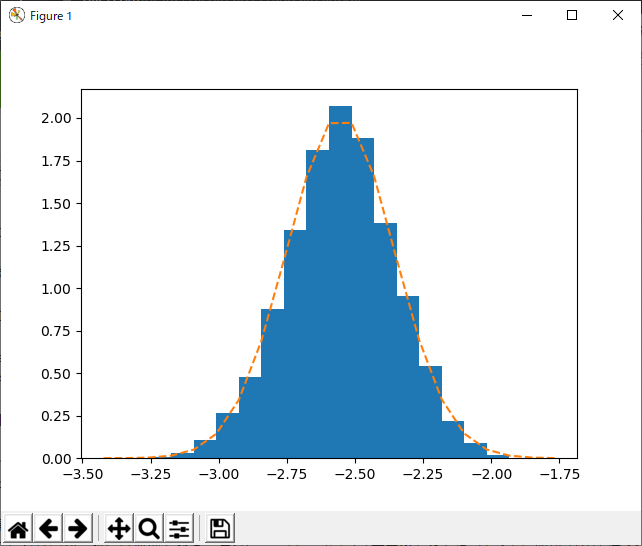
結果は次の通り。
どうやら、平均値の誤差は、奇麗な正規分布になるようである。さすが、中心極限定理。よかったよかった。このグラフを見ると、平均値の推定誤差がどの程度あるのかよく分かりますなぁ。
ちなみに、中央値についても同じような計算ができる。
元が変な分布なので、ちょっといびつだが、これが中央値の誤差の分布である。実際に母集団からもっと多くのサンプルを採取して、中央値を計算してみよう。
>>> samp1=np.log(np.random.normal(0.0,0.5,100000)**2);
>>> np.median(samp1)
-2.1762735168702765
あー、思ったより良くないかも。まあでも、こんな感じでとりあえずの誤差の分布を計算出来てしまうのが、ブートストラップ法のメリットである。
おわりに
勉強すればするほど、統計学って完ぺきに深く理解しない限り、「すきる」として活きないのでは?とういう気がしてきてしまう。若いうちにやっておくのならいいのだが、良い歳になってから始めることでもないかもなぁ。
ただ、興味はあるので、引き続き勉強しようと思う。