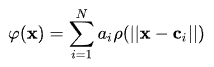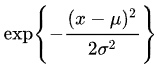表題の通り、放射基底ネットワークを作ってきたのでコードを晒すという話。英語が読めて、数式も読めて、でんでんむしの計算ができる人は、この記事を読む必要はないぞ！下のページを見ようね。

でんでんむしの計算が苦手な人（あと宿題サボりたいやつ）は裏技を教えるので、こうご期待だ。

関数近似

この世界には、関数近似という手法が存在します。関数をこう、うにょうにょーってやつで近似します。CGといえばBスプライン！という世代なのですが、今の人みんな知ってるのかな？ともかく、あんな感じで、指定された点を通る「なめらか」な曲線を計算によって生み出す！それが関数近似。連続性は何次まであるとか、universalな関数近似法か、とか結構深い理論がある分野なのですが、私が欲しいのは、k次元の入力に対して、スカラーを一つ返してくれるブラックボックスに過ぎません。というわけで、なるだけ簡単なのをと思って探していたところ、見つけたのが表題のやつ。

放射基底ネットワーク

ニューラルネットワーク「もどき」です。ただし、三層なので「あさい」。というわけで、学習も早そうだし、何しろ実装が楽そう。でかいライブラリもいらなそう。そして、なによりいじりやすそう。というので、試しに実装してみることに。仕組みは簡単で基底関数φ(x)というのに、重みをかけて足し合わせてyを計算します。式にすると：

図は英語版Wikipediaより拝借。φとか言っておきながら、ρになってますね。このρ(||x - c_i||)のようなやつが基底関数で、a_iみたいなのが重みです。

基底関数

基底関数は何でも良い（いや、多分条件とかあるけど、ほとんどなんでもいいはず）。これが、シグモイドなら、いわゆる元祖ニューラルネットワークです。なんか、ウェーブレットとかも使えそうだけど、使えるのかな？ただ、本日は皆さん大好きなガウス関数を使う前提で行きます。これです：

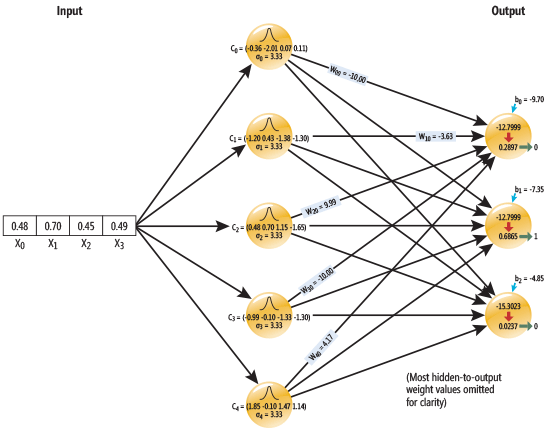
まず、データxを上記の関数に通して、そのあと重みをつけて足し合わせる。muとかsigmaはあらかじめ設定しておくこともできるし（関数形に見当がつく場合）、未知ならランダムにして適当に配置してもよい。図にするときかのような感じ。マイクロソフトのサイトから拝借。

というわけで計算は簡単ですね。次の通り：

phi_x = np.exp(-(mu - x)**2 / sigma**2)
# バイアス項があるので、最後に1を追加。
diff_x = np.r_[np.sum(phi_x,1),1.]
# 重みをかけて足す。
y_hat = diff_x @ self.w

ちなみに、np.sumのaxisが1になってるのは、xとしてk次元ベクトル、muとしてk次元ベクトル × n個の行列もどきを想定しているためです。np.sum(ほげほげ,1)とやると、「ほげほげ」をベクトルとみなして、それぞれの次元で和を取るみたいな動作になるので便利。そして、何より計算が速い。というわけで、見た目には分かりませんが、n個の基底関数の中心mu（k次元）があり、そこからx(k次元）を引き算して、sigma(n次元ベクトル）の二乗で割った後、「nについて」足し合わせ、みたいな動作をすることになっています。

関数近似

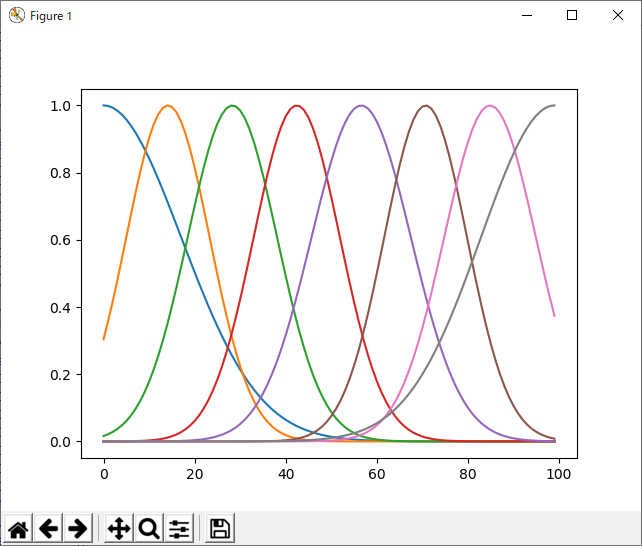
で、これの何が面白いのかというと、X軸上に上記のようにベルカーブを配置して、重みをつけて足し合わせることで、目的の関数f(x)の近似ができるということなのであーる。

こんなのからどうやってf(x)を作わけ？と思う人もいると思うけど、フーリエ変換やウェーブレット変換だって、波を足し合わせて波形を作っている（フーリエ変換は周波数ごとにたくさんの波を用意する。ウェーブレットは空間／時間軸上にウェーブレットをたくさん配置する、そして重みをつけて足し合わせ、のような感じ）。というわけで、やっていることはちょっと似ていると言えないこともない。

さて、何をやっているにしろ、関数ρでxを変換して、重みをかけて足し合わせるという動作なので、データをバッチで学習する場合、普通に二乗誤差の計算を「せんけいかいき」するのと同じ要領で出来ます。やったね。逆行列を計算するだけで終わり。

# 重みの掛け算はしない。てか、その重みを見つけようとしているので、当然。
phi = lambda x: np.r_[np.sum(np.exp(-((x-mu)*(x-mu))/(sigma**2)),1),1.] 
# データを行列っぽくずらーっと並べる。
H = np.apply_along_axis(phi, 1, X)
# ペナルティL1？だっけ？
L = np.diag(np.repeat(lam, H.shape[1]))
# 正規方程式とか言う名前のやつ。np.linalg.lstsqとかで計算してもいいかも。
self.w = np.linalg.inv(H.T @ H + L) @ H.T @ y

こうすると、重みが分かる。重みが計算出来たら、関数の補完は簡単にできる。

phi = lambda x: np.r_[np.sum(np.exp(-((x-mu)*(x-mu))/(sigma**2)),1),1.]         
H = np.apply_along_axis(phi, 1, X)
return H @ self.w

勾配法による学習

というわけで、バッチで学習するのはめっちゃ簡単なのだが、オンライン学習をしたいのである（私が）。そこで、「こうばい」とかを計算しないとならないのだが、私は「でんでんむし」が嫌いなので、SymPyというありがたいライブラリを使う。

SymPyはいわゆる「文字計算」をあなたに代わってコンピュータがやってくれる。かなりハイレベルな宿題のサボり方のようにも聞こえるが、僕らはもう大人だからね。わざわざ紙とノートで計算する必要はない（実際は、タブレットだのPCだのより、紙と鉛筆の方がめんどっちいことを考えるときにはよっぽど役に立つけどね！）。というわけで、計算はPCに丸投げしよう。

先ほど説明したように、これは「せんけいかいき」と同じ問題なので、このあいだSGDのところで説明したように、重みｗに関する「でんでんむし」の計算が必要になる。というわけで、誤差関数Eの微分をするのだが、微分には「ちぇいんるーる」というのがあったのでした。Tensor FlowとかChainerが自動でやってくれるんだった気がするあれですね。それが面倒なので、誤差関数の「なかみ」をSymPyに放り込んで計算させる。放射基底ネットワークの計算は次の通り（疑似コード）：

y = np.sum(w * np.exp((x - mu)*(x - mu) / (sigma**2)), 1)

これの誤差が欲しいのだから、移項して、

E = y - np.sum(w * np.exp((x - mu)*(x - mu) / (sigma**2)), 1)

とおく。本来、これをさらに二乗して、二乗誤差とするのだが、Eの微分は、∂E/∂w = 2 * E(x)なので、さすがの私でも暗算できる。面倒なのは、いわゆる微分の連鎖（チェインルール）が発動するので、上の式の後ろに∂x/∂wってのがついてしまうところ。xはwの関数ではない（wはexpの中に入ってないから）ので、この場合はxをそのまま書けばよい。結局∂E/∂w = 2 * E(x) * xとなり、めでたしめでたしである。ところが、今回は既定の位置muや幅sigmaのパラメータも調整したいのである。その場合、muとかsigmaはexp(~)の中にいるので、∂x/∂μとか、∂x/∂σを計算せねばならぬ。が、高校大学を卒業した今、そんな計算を手でやりたくはない→じゃあ、コンピュータ（SymPy）にやらせよう( ´∀｀ )。というのが、今回の趣旨である！（いつものように、でんでんむしは嫌いと言って逃げてはいけない、逃げちゃダメだ！という私の自己に対する戒めを兼ねて）

そして、これが（計算をサボるための）コード。

import sympy

x,y,mu,sigma,w=sympy.symbols('x,y,mu,sigma,w')

# 二乗誤差関数をEとすると、Eは(y-f(x,Θ))^2なので、微分の連鎖測、ちぇいんるーる
# によって、2(y-f(x,Θ))*∂E/∂Θと姿を変え、でんでんむしが出現する。
# Θはこの場合重みwだが、実は基底関数の中心μとかσについても最適化したいので、
# ∂E/∂wのほか、∂E/∂μとか、∂E/∂σの計算もせねばならぬ。それは嫌だ。そこでSymPyですよ！
err=y-w*sympy.exp(-(x-mu)**2/(sigma*sigma))

print(sympy.diff(err, w)) # ∂E/∂w
print(sympy.diff(err, mu)) # ∂E/∂μ
print(sympy.diff(err, sigma)) # ∂E/∂σ

>>> # できた
-exp(-(-mu + x)**2/sigma**2)
w*(2*mu - 2*x)*exp(-(-mu + x)**2/sigma**2)/sigma**2
-2*w*(-mu + x)**2*exp(-(-mu + x)**2/sigma**2)/sigma**3

というわけで、基底関数ネットワークのパラメータ、重みw、中心μ、幅σに関する更新の式が得られた。あとは、これをデータ一ごとに計算してあげれば、最適化ができるぞ。残念ながら、SymPyは計算の答えを教えてくれるだけなので、上の式をコードの変換するのは人間の私の仕事である。そこで、こんなふうにしてみた。

   # ...(略）...

    # stochastic gradient
    def update(self, x, y, alpha=0.005):
        w, mu, sigma = self.params()
        phi_x = np.exp(-(mu - x)**2 / sigma**2)     
        diff_x = np.r_[np.sum(phi_x,1),1.]
        diff_mu = -np.sum(w[:-1] * (mu - x) * phi_x / (sigma**2), 1)
        diff_s = np.sum(w[:-1] * ((mu - x)**2) * phi_x / (sigma**3), 1)      
        diff_mu = diff_mu.reshape(self.mu.shape)
        #diff_mu = np.array([diff_mu]).T
        # update w, mu, sigma        
        y_hat = diff_x @ self.w
        self.w += alpha * (y - y_hat) * diff_x       
        self.mu += alpha * (y - y_hat) * diff_mu   
        self.sigma += alpha * (y  - y_hat) * diff_s

SymPyが出してくれた答えを、Pythonに翻訳するだけの、簡単なお仕事です。

うごかしてみる

すんなり動いたような書き方をしているが、結構大変だった。いやね、ちゃんと計算したにもかかわらず、なんか、実装するときに符号とか、インデックスとか色々間違えたりなんだりで…。でもまぁ、普通にできました。

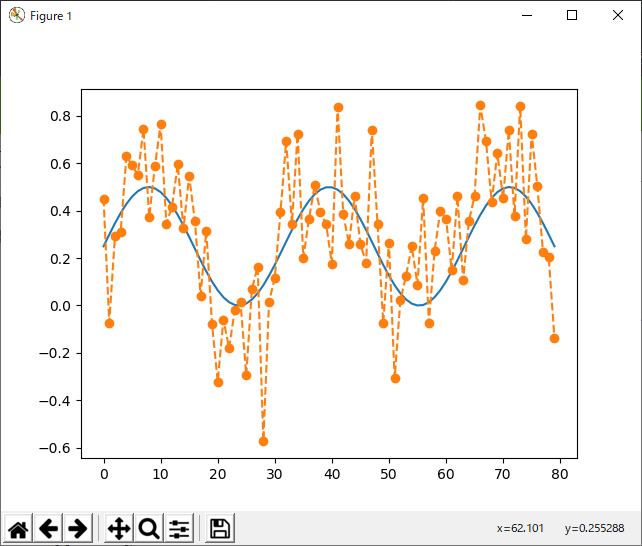
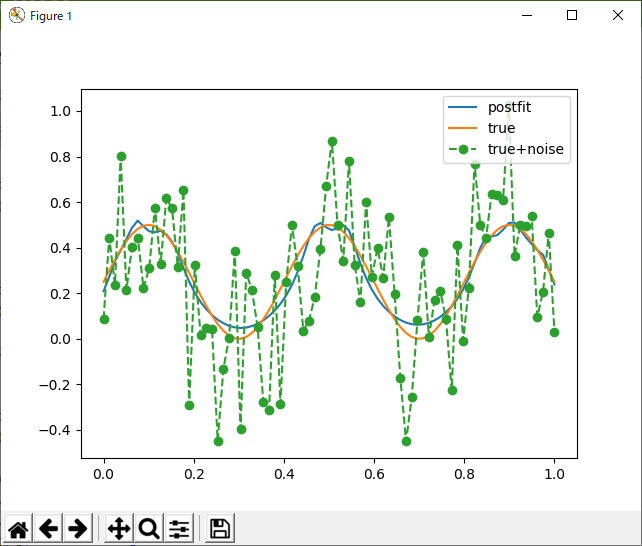
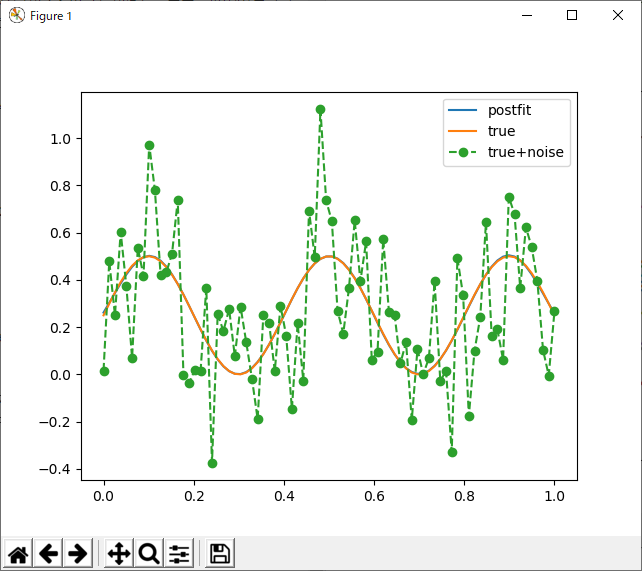
とりあえず、例題として、ノイズが山ほど載ったsin関数を選ぶ。基本的に最小二乗推定なので、ノイズが載っていても、データ数がそれなりであれば、ちゃんと補完できるはず。もちろん、sin波の周波数が大きくなればなるほど、高い解像度＝たくさんの基底関数が必要になると想定される。この場合、とりあえず基底は12個にしてみる。

とりあえず、学習できている模様。では、半分の六個ならどうでしょう？

基底が足りないせいで、無理くりデータを近似しようとして、おかしなことになっている。でも、六個だよ？ベルカーブ六個、上手いこと足し合わせたら、こぶが三つのサインカーブくらいなんとか近似できそうな気がするけどなぁ。ただ、グラフを見た感じノイズに引っ張られているような気もする。かわいそうなので、周期を半分にしてあげる。

当然と言えば当然だけど、今度はうまく行った。

学習器の性質

色々いじってみてわかったんだけど、初期値にすげー敏感。はじめは、均等に並んでるところから始めた方がいいと思って、サインカーブを色々学習させてみたんだけど、均等に並べるより、ランダムの方が良い結果が出る（少ない基底で、良い近似ができるという意味。基底をたくさん使えば、たいていどうにでもなるが、それだとねー、あんまり強みがない）。ただし、ガウス基底の分散を、ちょうどいい感じにばらけさせてやらないと、今度は全然学習できない（過学習というのとも違うと思う…バグが？）。

ランダムな基底による検証

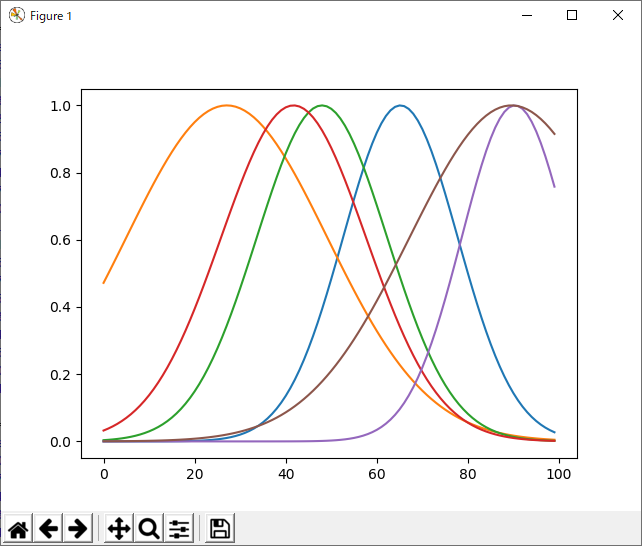
下の図は、ガウス基底の分散を1/N（Nは基底の数）、ガウス基底の中心を、0~1の一様乱数として初期化した場合の結果。

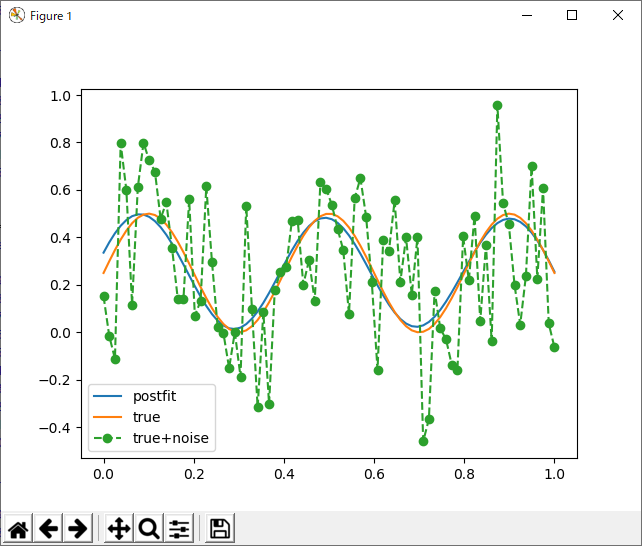
これで、80点のデータを1024回（データ順のランダム化はせず）無理くり学習させてみると、このようになる。

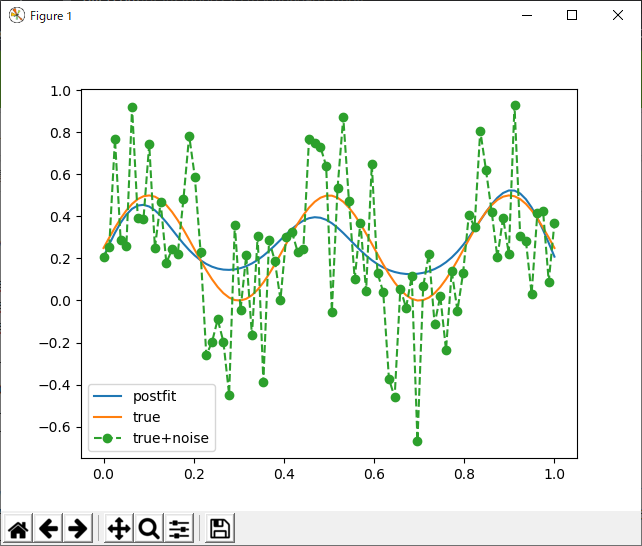
基底が六個なので、わりと良い方だと思われるけど、1024回もループ回してこれってのはちょっとがっかり。もう一度実行してみると、またちょっと違った結果が得られる。

サインカーブの三つの「こぶ」のうち、真ん中と右端のやつは、上手く基底関数の中心にとらえられているが、これがうまく行くかどうかは、初期配置に依るっぽい。関数のピークにある程度めどがついているのなら、これでも良いと思うのだが、全く何のめどもついていない場合、基底関数を増やすしかない。一番残念だったのは、元のデータの特性を、ガウス基底がうまく表現してくれる(代表点のようなものを抽出できる）わけでもないというのがわかったこと。特に基底の数が多いと、ごり押しでフィッティングするため、データの構造など全く反映されない。

かといって、基底を多くしすぎると、今度は変なところにピークが出たりする。もしかすると、ノイズを過学習しているのかもしれない。対策としては、単にランダムに規定を配置するのではなく、区間をN個に区切ってジッターをかけるとか、そういう前処理が必要になりそう。フィルタかけたら？と思う人もいるかもしれないが、オンラインで、部分的にしかデータが得られない場合のフィッティングを考えているので、それは不可能。つまり、関数f(x)のxが順番ではなく、ランダムに来るような状態でf(x)の全貌を学習したいということ。今はデータの並びをランダム化していないのでアレだけど、もしかするとランダム化した方がいい結果が得られるのかもしれない。その辺は、後々。ただ、じゃあデータxが常にランダムに来るのかというとそうでもなく、ある程度自己相関のある状態で入ってくることも予想されるから、あまり順番には依存しないアルゴリズムのほうがいいと言えばいい。

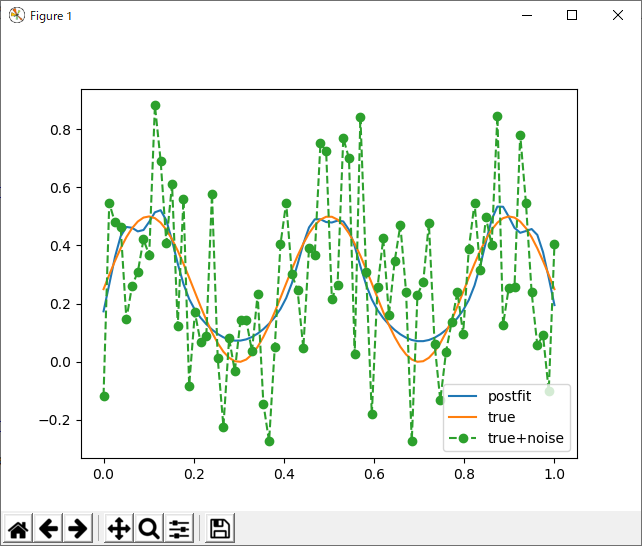
ちなみに、無駄に基底を多くとりすぎるとこうなる（１２個。ただし、これもダイス目による。乱数の性質が良ければ、うまく行く）。

何らかの正則化をつけて、|w|が小さい場合は、強制的にゼロという対策も考えられそうだが、こうやってTODOリストに「やるべきこと」がたまってしまうようなアルゴリズムはやだなぁ。クイックソートとか使う時、細かいチューニングなんてしないもの。

一様な基底による検証

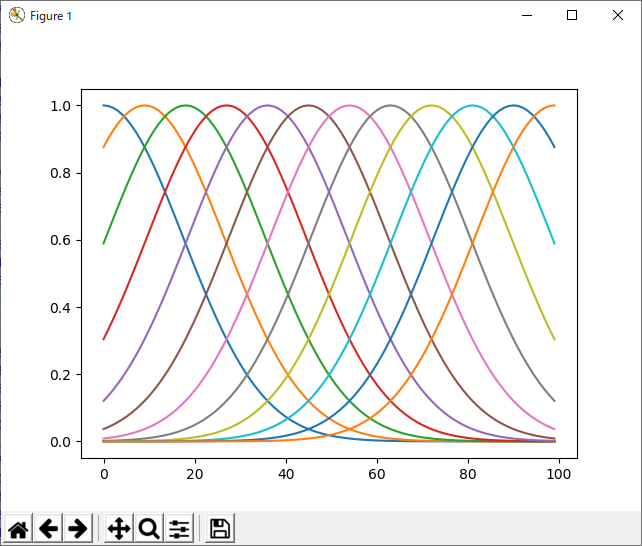
ただし、基底を山ほど使っていいという前提なら、最も安定するのはたくさんの基底を規則正しく並べて、既定の中心や幅は学習せず、重みだけを学習するというやり方。そうすると、大抵の場合、安定して関数の近似ができる。ただ、それだと高次元になったとき行き詰まるのは目に見えているから、正直それはやりたくない。そもそも、基底の位置や幅まで学習可能なこのアルゴリズムに目をつけたのは、少ない基底でf(x)を近似できるのなら、xが高次元でも、基底を特徴点としてみることで、データの特徴が取り出せるのではないか？と思ったからだ。まー、世の中そううまくはいかないってこと？（ただ、そういうことができるという触れ込みのアルゴリズムでもあった気がする）。

ちなみに、これが均等な基底で学習した場合の結果：

ベルカーブも規則正しく並べると、ちょっとアーティスティックである。

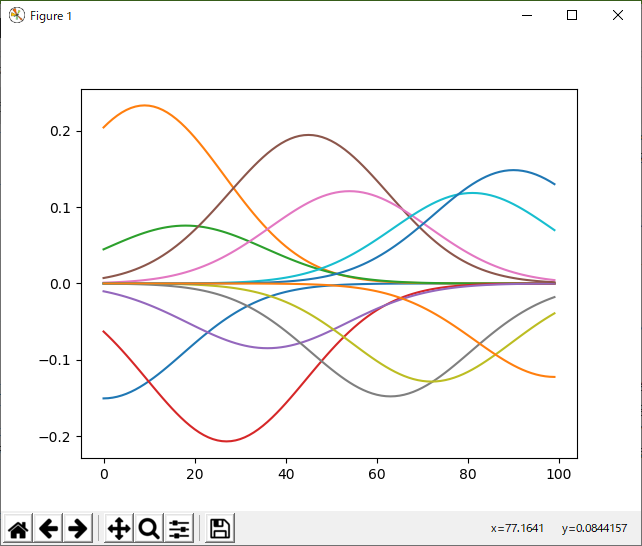
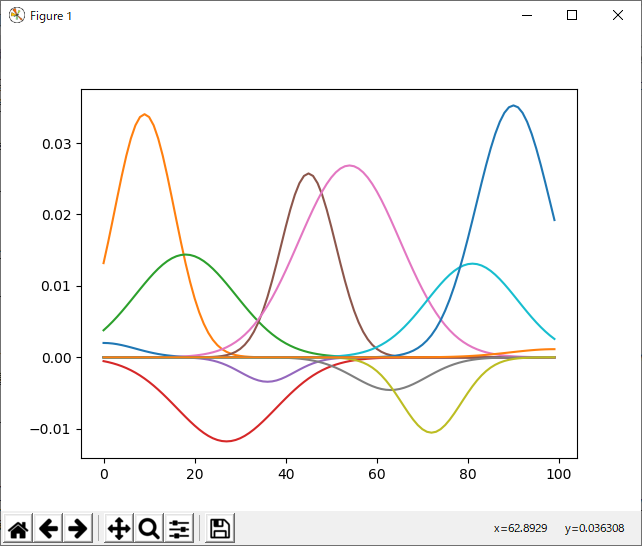
これだと、なんかい回してもだいたい上記のような結果になる。あと、学習はSGDで勾配を更新しているだけなので、めちゃくちゃ速い。ただし、こういう状態で重み付けされた基底をみても、得られるものはない。

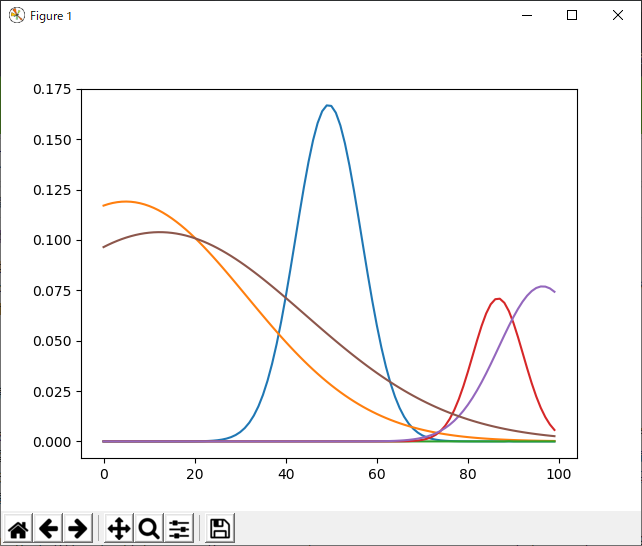
どうみても、これが上記のサインカーブの特徴を反映しているようには思えない。ようするに、タダのカーブ・フィッティングであり、未知のデータから有用な情報を取り出すのには使えないのではないか？という気がする。ちなみに、基底の中心を規則的にしても、幅はランダム化した方が良いように思える（何回か実験した結果）。

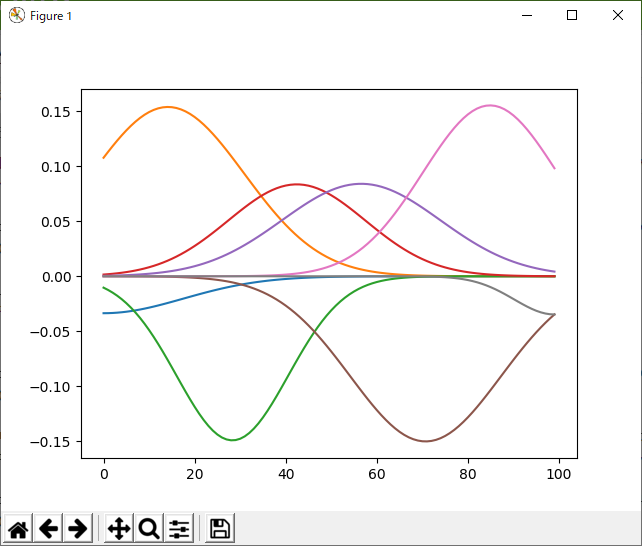
この場合も、基底の中心は固定されていて、重みだけ変えているので、ダイス目によって結果が大きく変わるということはなく、分散を適当に（固定で）割り振る場合に比べても結果が良い。そして、なにより、重み付けされた基底がちゃんとデータの傾向を反映している。

もしかすると、最初に「固定」で割り振った基底関数の幅が大きすぎたのかも。ただ、重ねて言うが、そもそもf(x)が未知の状態で学習することを考えているのだから、基底の幅としてどの程度がいいか？なんて最初から分かるわけはない。そこまで考え合わせると、ある程度の幅でランダム化した方が、良い結果が得られるかもしれない。

分散のみランダム化

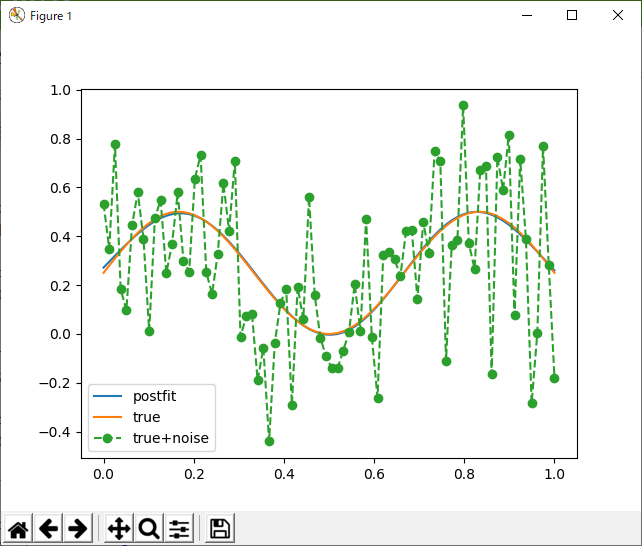
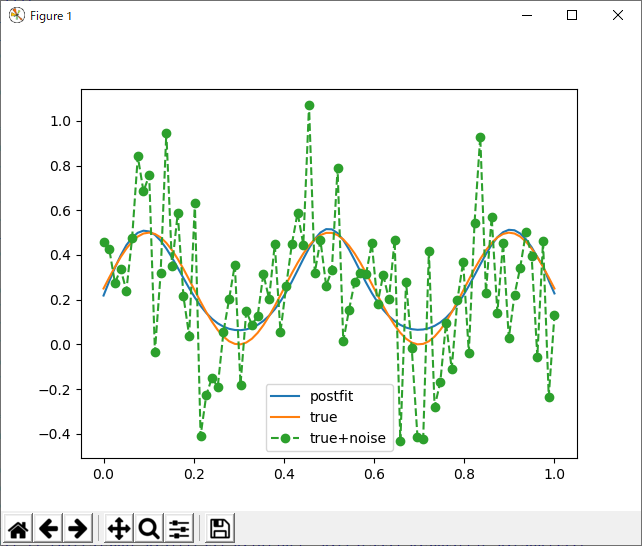
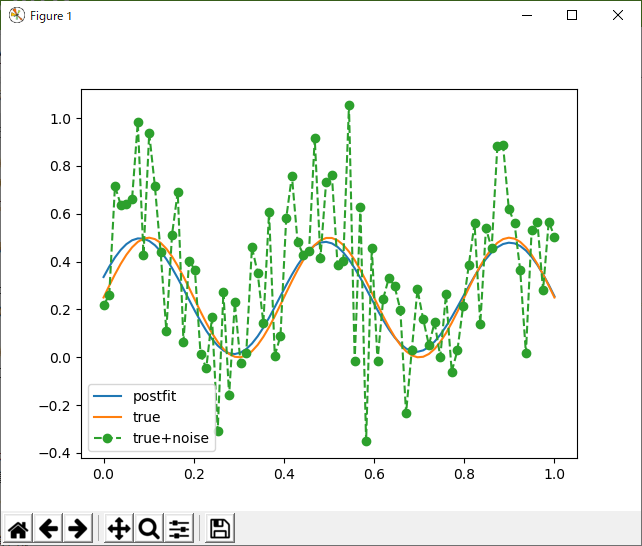
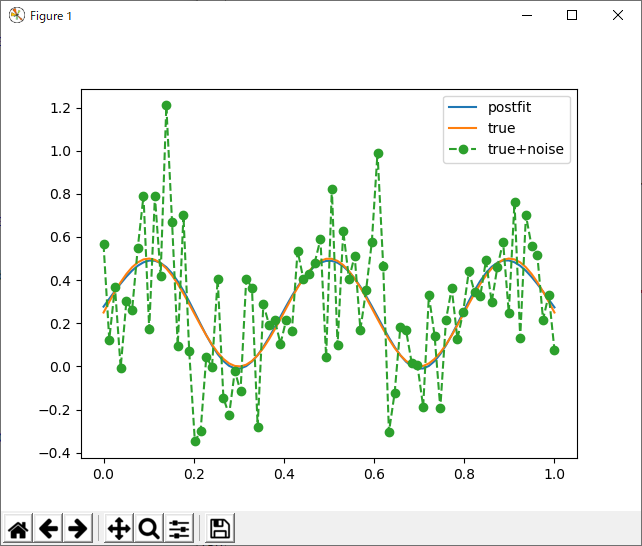
基底の位置を固定にして、分散のみをランダム化、重みと基底の位置、両方を学習。既定の数は八個。

毎回、このくらいのクオリティーを出してくれるのなら、手放しで「オススメ」できるのだが、これはかなりうまく行った方。見ての通り、元の関数の対称性を再現するように、基底関数の位置や幅が学習されている。こーゆーのを機械学習というのだよね。毎回こういう結果が得られるなら、再現性においても、知識の抽出という面においても優れていると言えるんだけどなー。なんか不安定なんだよね、これ。

まとめ

放射基底ネットワークを実装して、色々やってみたところ：

一応、便利といえば便利。割と少ない労力で関数近似ができる。
けれども、基底の数が結構多めじゃないとうまく行かない。
近似（学習）したい関数が未知の場合、基底の初期配置を工夫する必要がある。
わりと均等に配置して、分散をある一定の範囲でランダムに割り振ると効果的。

などということが分かった。

あと、今回の教訓は、なんでもそうだけど、学習器の仕組みはちゃんと把握しておくということ（自前で実装する必要まではないかもしれないけど）。一見ちゃんと動いているように見えても、学習器が、きちんとデータの構造を学習しているかどうか？については、「中身」を覗いてみないと分からないことも多い。sklearnで適当にRegressorやClassifierを使っているだけだと、そういうことに気づかないし、でんでんむしとも疎遠になってしまう。今回は、自前でパラメータの更新式を計算…じゃねーや、さぼってSymPyにやってもらったのだが、計算はできなくとも「どういう計算をすればよいか」くらいは分かってないと、やっぱりダメだよねー。とういうことで、数式アレルギーを克服しようと思います。

では、また！