対象読者
基本的なビット演算は理解していて、C#での高速なビット演算に興味があるという方を対象にしています。
最初に結論
BitOperations.PopCount を使いましょう。専用命令 popcnt を使用して計算するので最速です。popcnt が使用出来ない場合でも、最適化されたソフトウェアフォールバックを実装しています。
どの程度速いのか?
安直にビットカウントするなら、ループで元の値を右シフトしながら、最下位ビットをAND演算で取り出して数える、みたいな処理を思いつくんじゃないでしょうか。
private int PopCnt_LoopShift(uint value)
{
int result = 0;
for (; value > 0; value >>= 1)
{
result += (int)(value & 1);
}
return result;
}
こんな感じですかね。
BitOperation.PopCount は前述のとおり、使用可能なら popcnt 命令が使用されますが、公式githubのソフトウェアフォールバックの処理を見てみます。
static int SoftwareFallback(uint value)
{
const uint c1 = 0x_55555555u;
const uint c2 = 0x_33333333u;
const uint c3 = 0x_0F0F0F0Fu;
const uint c4 = 0x_01010101u;
value -= (value >> 1) & c1;
value = (value & c2) + ((value >> 2) & c2);
value = (((value + (value >> 4)) & c3) * c4) >> 24;
return (int)value;
}
0x55555555 や、0x33333333 と謎の定数が出てきたり、もう訳が判りませんね!
いかにも最適化されてそうな雰囲気がします。
とりあえず乱数10万件のビットカウントを計測した結果、以下のようになりました。
| Method | Mean | Error | StdDev |
|---|---|---|---|
| PopCntInstruction | 65.14 μs | 7.261 μs | 0.398 μs |
| SoftwareFallback | 175.81 μs | 36.117 μs | 1.980 μs |
| LoopShift | 1,711.86 μs | 26.055 μs | 1.428 μs |
安直なループ+シフト処理と比較すると、popcnt命令だと26.3倍、ソフトウェアフォールバックでも9.7倍高速です。専用命令無しでも、ここまで速いのが驚きです。
ソフトウェアフォールバックを分析する
ソフトウェアフォールバックの謎の定数などについて考えていきます。
【ここがすごい1】減算でビットカウント
ソフトウェアフォールバックの最初の行の計算を見ると、このようになっています。
value -= (value >> 1) & 0x_55555555u;
0~3の数値は2bitで表現出来ますが、bitで表現される数値から2進数の上位1bitの値を引くと、ビットカウントと一致します。
| 10進数 | 2進数 | ビットカウント(式) |
|---|---|---|
| 3 | 11 | 2(3-1) |
| 2 | 10 | 1(2-1) |
| 1 | 01 | 1(1-0) |
| 0 | 00 | 0(0-0) |
0x55555555 は、2進数表現だと 01010101010101010101010101010101 となり、01を交互に繰り返している数値です。valueを>>1して、0x55555555 とANDを取る事により、上位1bitが下位に移動されます。

元のvalueからこの値を引く事により、2bit×16個を並列にビットカウントしている訳ですね。
実際に、適当な乱数で計算前と計算後のビットの値を実際に確認してみます。
using System;
using System.Numerics;
uint value = (uint)new Random().Next();
Console.WriteLine($"[計算前] 2進数:{Convert.ToString(value, 2).PadLeft(32, '0')} 16進数:0x{value:X8} PopCount:{BitOperations.PopCount(value)}");
value -= (value >> 1) & 0x_55555555u;
Console.WriteLine($"[計算後] 2進数:{Convert.ToString(value, 2).PadLeft(32, '0')} ");
Console.ReadKey();
// 出力結果
// [計算前] 2進数:00110111101111001011101100110000 16進数:0x37BCBB30 PopCount:18
// [計算後] 2進数:00100110011010000110011000100000

2bitで区切った数の合計が、PopCountと見事に一致しました。それにしても、よくこんな事を思いつくなと感心しますね。もしこれを加算で計算するなら、
value = (value & 0x55555555) + ((value >> 1) & 0x55555555);
のようになると思いますが、AND演算が余分に増えてしまいます。
少しでも演算を減らすための減算という訳ですね。
| 16進数 | 2進数 |
|---|---|
| 0x33333333 | 00110011001100110011001100110011 |
| 0x0F0F0F0F | 00001111000011110000111100001111 |
こうして2進数にしてみると、他の定数も何の為にあるのか見えてきますね。
2bit×16個 ⇒ 4bit×8個 ⇒ 8bit×4個 と、右シフトしてAND演算で定数をマスクしながら上位から下位へ次々とビットカウントを合計しているようです。
【ここがすごい2】0x01010101 を乗算して上位8bitで合計処理
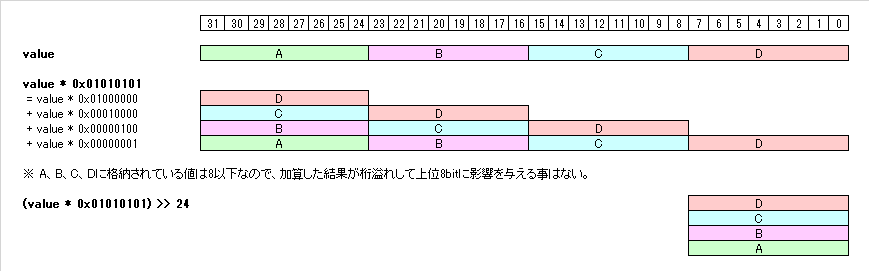
このまま右シフト・AND演算・加算の流れが続いていくかと思いきや、0x01010101 の乗算が出現しました。これも演算を減らすための工夫で、図にするとこうなります。
乗算1回と右シフト1回だけで、残りの8bit×4個のビットカウントを一気に合計しています。残りを右シフト+AND演算で切り出して加算していくより、こちらの方が速いようです。
最初に処理全体を見た時は訳が分かりませんでしたが、一つ一つを分解していくと実に理に適っていて、極限まで無駄を省いたすごい実装だと思いました。ただまあ、これを自力で思いつくかと言われたら、絶対無理ですね!
参考資料
Wikipedia - Hamming weight
Wikipedia - x86 Bit manipulation instruction set
Counting bits set, in parallel
Stack Overflow - How to count the number of set bits in a 32-bit integer?