この記事はJuliaLang Advent Calendar 2022 15日目の記事です。
誤差伝播って面倒だよね
実験の測定値に誤差はつきものです。その測定値から別の物理量を計算する際にも、誤差を適切に伝播させる必要があります。今回は測定値を誤差付きで管理し、線形誤差伝播を自動で行うパッケージMeasurements.jlを紹介したいと思います1。適宜公式ドキュメントを参照してください。
簡単な使い方
julia> using Measurements
julia> x = 1 ± 0.1
1.0 ± 0.1
julia> typeof(x)
Measurement{Float64}
julia> y = measurement(2 ± 0.1)
2.0 ± 0.1
測定値±誤差やmeasurements(val, [err])などで宣言できます2。errは標準偏差(および標準偏差だと思われるもの)です。型はMeasurement{T}でT<:AbstractFloatで、Measurement<:AbstractFloatです。
julia> x + y
3.0 ± 0.14
julia> x - y
-1.0 ± 0.14
julia> sin(x)
0.841 ± 0.054
julia> x - x
0.0 ± 0.0
なんか普通の計算で誤差を含めて計算されてることはわかりますが、そもそも線形誤差伝播が何なのかがわからないと妥当なのか判断しかねるので、軽く線形誤差伝播について説明したいと思います。
線形誤差伝播とは
物理量$Y, X_1, X_2, \cdots, X_N$の間に、
Y = F \left( X_1, \cdots, X_N \right)
なる関係が成り立っているとします。$X_i$の真の値が$\bar{X_i}$であり、$X_i$の誤差、すなわち$X_i - \bar{X_i}$が小さいならば、
\begin{align}
\bar{Y} &= F \left( \bar{X_1}, \cdots, \bar{X_N} \right) \\
Y - \bar{Y} &= F \left( X_1, \cdots, X_N \right) - F \left( \bar{X_1}, \cdots, \bar{X_N} \right) \\
&\simeq \sum_{i=1}^N \left. \frac{\partial F}{\partial X_i} \right|_{X_i = \bar{X_i}} \left( X_i - \bar{X_i} \right)
\end{align}
が成り立つので、$Y$の分散$\sigma_Y^2$は
\sigma_Y^2 = \sum_{i \neq j} \left. \frac{\partial F}{\partial X_i} \right|_{X_i = \bar{X_i}} \left. \frac{\partial F}{\partial X_j} \right|_{X_j = \bar{X_j}} \sigma_{ij} + \sum_{i}^N \left. \left( \frac{\partial F}{\partial X_i} \right|_{X_i = \bar{X_i}} \sigma_{i} \right)^2
となります。ただし、$\sigma_{ij}$は$X_i$と$X_j$の共分散、$\sigma_i^2$は$X_i$の分散です。
通常は更に$X_i$が独立であることを仮定して、共分散が$0$になることから、
\sigma_Y^2 = \sum_{i}^N \left. \left( \frac{\partial F}{\partial X_i} \right|_{X_i = \bar{X_i}} \sigma_{i} \right)^2
の式を用います。
計算結果の検証
線形誤差伝播について理解したところで最初の例の結果を検証してみます。
julia> x = 1 ± 0.1
1.0 ± 0.1
julia> y = measurement(2 ± 0.1)
2.0 ± 0.1
julia> x + y
3.0 ± 0.14
julia> x - y
-1.0 ± 0.14
$x + y$はそれぞれの偏微分は$1$になるので、標準偏差は$\sqrt{(1 \times 0.1)^2 + (1 \times 0.1)^2} = 0.1 \times \sqrt{2}$なので計算結果と一致しました。$x - y$の方はそれぞれの偏微分は$1, -1$になりますが、分散を求めるときに2乗の和を求めてるので、誤差は$x + y$のときと同じになります。
julia> sin(x)
0.841 ± 0.054
$\sin$の微分は$\cos$なので、分散は$\cos(1) * \left| 0.1 \right| = 0.054$で一致します。
julia> x - x
0.0 ± 0.0
この結果はどうなるでしょうか。一見すると間違ってるように思いますが、分散を求める式を導出する際に変数の独立性を仮定していたので、この場合は誤差は正確に$0$になります。
このようにMeasurements.jlは普通の数値計算をするように書くだけで誤差伝播をしてくれる便利なパッケージです。他にどんな関数のメソッドが定義されてるか気になりますがmethodswith(Measurements)を見ると標準でも238個ほどあるようでした。
ちなみに、Measurementから測定値や誤差を取り出したいときはMeasurements.valueやMeasurements.uncertaintyを使います。
julia> Measurements.value(x)
1.0
julia> Measurements.uncertainty(x)
0.1
他のパッケージと
Measuremnts.jl単体でも十分に便利なパッケージですが、Juliaらしく他のパッケージとの連携においてもMeasurements.jlは便利なパッケージです。
StatsBase.jlと一緒に使う
(追記) 平均値と標準偏差からMeasurementを作るときに若干便利になる関数mean_and_stdなどがあります。
julia> using StatsBase
julia> xs = collect(1:10)
10-element Vector{Int64}:
1
2
3
4
5
6
7
8
9
10
julia> mean(xs) ± std(xs)
5.5 ± 3.0
julia> measurement(mean_and_std(xs)...)
5.5 ± 3.0
SpecialFunctions.jlと一緒に使う
特殊関数でも使えます。
julia> using SpecialFunctions
julia> gamma(x)
1.0 ± 0.058
julia> airyai(x)
0.135 ± 0.016
Unitful.jlと一緒に使う
測定値、物理量といったら、その単位や次元にも気を配る必要があります。そんなときに便利なのがUnitful.jlです。
julia> using Unitful
julia> z = 1*u"m"
1 m
julia> typeof(z)
Quantity{Int64, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}
@u_strを用いて単位を含めた変数を作ることができ3、その型はQuantity{T, D, U} <: Numberで、Tが数値の型、Dは次元、Uは単位を表します。PhysicalConstants.jlの値もUnitful.AbstractQuantityのsubtypeとなっており、物理定数もシームレスに統合した計算ができます。
Unitful.jlと一緒にMeasurements.jlを使う際は、特に何も考えずに使えます。
julia> x = 10u"m" ± 200u"mm"
10.0 ± 0.2 m
julia> typeof(x)
Quantity{Measurement{Float64}, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}
julia> y = 2u"s"±3u"ms"
2.0 ± 0.003 s
julia> x/y |> u"m/s"
5.0 ± 0.1 m s^-1
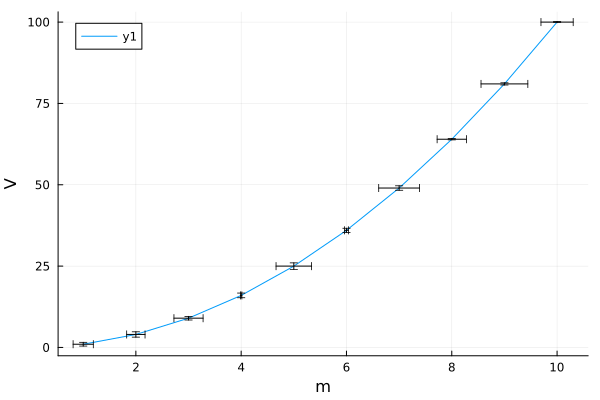
Plots.jlと一緒に使う
Measurements.jlにはPlots.jlのrecipe4が標準でついており、プロットにエラーバーを自動でつけてくれます。
julia> xs = [i ± rand() * 0.5 for i in 1:10] .* u"m"
10-element Vector{Quantity{Measurement{Float64}, 𝐋, Unitful.FreeUnits{(m,), 𝐋, nothing}}}:
1.0 ± 0.19 m
2.0 ± 0.17 m
3.0 ± 0.28 m
4.0 ± 0.014 m
5.0 ± 0.34 m
6.0 ± 0.036 m
7.0 ± 0.39 m
8.0 ± 0.28 m
9.0 ± 0.44 m
10.0 ± 0.31 m
julia> ys = [i^2 ± rand() for i in 1:10] .* u"V"
10-element Vector{Quantity{Measurement{Float64}, 𝐋^2 𝐌 𝐈^-1 𝐓^-3, Unitful.FreeUnits{(V,), 𝐋^2 𝐌 𝐈^-1 𝐓^-3, nothing}}}:
1.0 ± 0.57 V
4.0 ± 0.81 V
9.0 ± 0.55 V
16.0 ± 0.71 V
25.0 ± 1.0 V
36.0 ± 0.63 V
49.0 ± 0.69 V
64.0 ± 0.19 V
81.0 ± 0.34 V
100.0 ± 0.17 V
julia> plot(xs, ys)
Plot{Plots.GRBackend() n=1}
とても便利です!5
Latexify.jl, LaTeXStrings.jlと一緒に使う
Latexify.jlはJuliaの式を$\LaTeX$形式に変換するパッケージで、プロットに$\LaTeX$形式の文字列を埋め込むのに便利です。Measurementは問題なくlatexifyできます。
julia> x = 1 ± 0.1
1.0 ± 0.1
julia> latexify(x)
L"$1.0 ± 0.1$"
julia> using LaTeXStrings
julia> x = 10u"m" ± 200u"mm"
10.0 ± 0.2 m
julia> L"x = %$x"
L"$x = 10.0 ± 0.2 m$"
しかし、Quantity{Measurements, D, U}はうまくlatexifyできません。結果をみたらわかるとおりこのままでは斜体になってしまいます。そのためにUnitfulLatexifyというパッケージがありますが、これはMeasurementに対応していないため、誤差が表現されません。
julia> using UnitfulLatexify
julia> L"x = %$x"
L"$x = 10.0 ± 0.2 m$"
julia> latexify(x)
L"$10\;\mathrm{m}$"
GLM.jl
GLM.jlはそのままではMeasurementを扱えません6。このような場合はMeasurements.valueで測定値のみを取り出す必要があります。
julia> xs = [i ± rand() * 0.5 for i in 1:10]
10-element Vector{Measurement{Float64}}:
1.0 ± 0.11
2.0 ± 0.00095
3.0 ± 0.049
4.0 ± 0.46
5.0 ± 0.45
6.0 ± 0.33
7.0 ± 0.41
8.0 ± 0.13
9.0 ± 0.083
10.0 ± 0.13
julia> ys = [i * 0.5 ± rand() for i in 1:10]
10-element Vector{Measurement{Float64}}:
0.5 ± 0.014
1.0 ± 0.84
1.5 ± 0.15
2.0 ± 0.71
2.5 ± 0.19
3.0 ± 0.79
3.5 ± 0.46
4.0 ± 0.71
4.5 ± 0.29
5.0 ± 0.44
julia> using GLM, DataFrames
julia> df = DataFrame(:x => xs, :y => ys)
10×2 DataFrame
Row │ x y
│ Measurem… Measurem…
─────┼─────────────────────────
1 │ 1.0±0.11 0.5±0.014
2 │ 2.0±0.00095 1.0±0.84
3 │ 3.0±0.049 1.5±0.15
4 │ 4.0±0.46 2.0±0.71
5 │ 5.0±0.45 2.5±0.19
6 │ 6.0±0.33 3.0±0.79
7 │ 7.0±0.41 3.5±0.46
8 │ 8.0±0.13 4.0±0.71
9 │ 9.0±0.083 4.5±0.29
10 │ 10.0±0.13 5.0±0.44
julia> reg = lm(@formula(y ~ x), df)
ERROR: MethodError: no method matching Float64(::Measurement{Float64})
Closest candidates are:
(::Type{T})(::Real, ::RoundingMode) where T<:AbstractFloat at rounding.jl:200
(::Type{T})(::T) where T<:Number at boot.jl:772
(::Type{T})(::AbstractChar) where T<:Union{AbstractChar, Number} at char.jl:50
...
Float64への変換ができずにエラーがおきています。
julia> transform!(df, :x => ByRow(Measurements.value));
julia> transform!(df, :y => ByRow(Measurements.value))
10×4 DataFrame
Row │ x y x_value y_value
│ Measurem… Measurem… Float64 Float64
─────┼───────────────────────────────────────────
1 │ 1.0±0.11 0.5±0.014 1.0 0.5
2 │ 2.0±0.00095 1.0±0.84 2.0 1.0
3 │ 3.0±0.049 1.5±0.15 3.0 1.5
4 │ 4.0±0.46 2.0±0.71 4.0 2.0
5 │ 5.0±0.45 2.5±0.19 5.0 2.5
6 │ 6.0±0.33 3.0±0.79 6.0 3.0
7 │ 7.0±0.41 3.5±0.46 7.0 3.5
8 │ 8.0±0.13 4.0±0.71 8.0 4.0
9 │ 9.0±0.083 4.5±0.29 9.0 4.5
10 │ 10.0±0.13 5.0±0.44 10.0 5.0
julia> reg = lm(@formula(y_value ~ x_value), df)
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}, Vector{Int64}}}}, Matrix{Float64}}
y_value ~ 1 + x_value
Coefficients:
──────────────────────────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
──────────────────────────────────────────────────────────────────────────────────────────────
(Intercept) 1.65793e-15 5.726e-16 2.90 0.0200 3.37516e-16 2.97835e-15
x_value 0.5 9.22828e-17 5418128751070800.00 <1e-99 0.5 0.5
──────────────────────────────────────────────────────────────────────────────────────────────
これで問題なく計算できました。
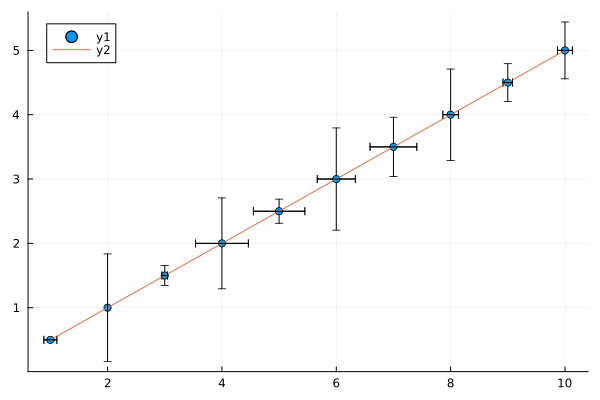
julia> plot(xs, ys, seriestype = :scatter)
Plot{Plots.GRBackend() n=1}
julia> plot!(xs, predict(reg))
Plot{Plots.GRBackend() n=2}
仕組み
魔法のように便利なMeasurements.jlですが、きっと皆さんは仕組みが気になってることでしょう。ということで詳しいことはAppendix - Measurementsにかかれてますが、その内容をかいつまんで紹介したいと思います。
Measurement型
まず基本的な型であるMeasurement型がなんの情報を保持してるかを説明します。
struct Measurement{T<:AbstractFloat} <: AbstractFloat
val::T
err::T
tag::UInt64
der::Derivatives{T}
end
valは測定値、errは誤差でここまでは簡単に想像できます。肝となるのはtagとderで、tagには固有の測定値ごとに一意なタグが、derにはその値が依存する全ての独立な測定値の(val, der, tag)をkeyに、その偏微分係数をvalueにもつDictが入ってます。他の測定値から計算された測定値のtagは0になっています。
まとめると、Measurementは固有の測定値の場合は一意なtagと、依存する全ての固有の測定値およびその偏微分係数を保持していることになります。簡単に確認してみると、
julia> x = 1 ± 0.1
1.0 ± 0.1
julia> y = measurement(2 ± 0.1)
2.0 ± 0.1
julia> z = 2x^2 + y
4.0 ± 0.41
julia> x.tag
0x00000000000000af
julia> y.tag
0x00000000000000b0
julia> x.der
Measurements.Derivatives{Float64} with 1 entry:
(1.0, 0.1, 0x00000000000000af) => 1.0
julia> y.der
Measurements.Derivatives{Float64} with 1 entry:
(2.0, 0.1, 0x00000000000000b0) => 1.0
julia> z.der
Measurements.Derivatives{Float64} with 2 entries:
(2.0, 0.1, 0x00000000000000b0) => 1.0
(1.0, 0.1, 0x00000000000000af) => 4.0
julia> z.tag
0x0000000000000000
と、たしかに
-
xとyのtagは異なっており、xとyに依存したzのtagは0になっている -
zのderにはx, yの(val, err, tag)とそれぞれの偏微分係数($x$は$\left. \frac{\partial (2x^2 + y)}{\partial x} \right|_{x = 1.0} = 2 \times 2 \times 1.0 = 4.0$, $y$は$1.0$)になってる
ことが分かりました。
つまり、Measurements.jlは
- 固有の測定値には一意なタグをつけて区別し、
- 他の測定値に依存した測定値は、固有な測定値とその偏微分係数を(必要があればそこまで還元して)求めて、自信の誤差を計算し、
- それを保存して、より後の計算へと継承
という過程で誤差を伝播させています。
関数のメソッドの実装
では、このような計算を行うmethodを各関数に対して定義するにはどうすればよいでしょうか。簡単にするために1つの固有な測定値のみに依存する2つの物理量について考えます。数式で書くと
\begin{align}
y &= f(x) \\
z &= g(y)
\end{align}
となっているとします。
$y$については、$f(x)$と$\frac{\partial f(x)}{\partial x}(x)$がわかれば、具体的な値$x = a \pm \sigma_a$に対して計算することができます。そして同様に、$z$について計算するには、依存している固有な測定値は$x$なので、$g(f(x))$と$\frac{\partial g(f(x))}{\partial x}$がわかる必要があります。$g(f(x))$自体は既存の実装だけで簡単に計算できますが、$\frac{\partial g(f(x))}{\partial x}$については既存の実装はありません。しかし、連鎖律から、
\left. \frac{\partial g(f(x))}{\partial x} \right|_{x=x_0} = \left. \frac{\partial g(y)}{\partial y} \right|_{y = f(x_0)} \left. \frac{\partial f(x)}{\partial x} \right|_{x = x_0}
が成り立つので、各関数$g, f$に対して、$g$, $f$自体と$g$,$f$の導関数が実装されていれば、Measurementの計算、そして誤差伝播ができることがわかります。一般の2個以上の引数を持つ関数についても全ての引数について導関数がわかれば良いです。
実際の実装はMeasurements.result(val, der, a)という関数で行われており、
cos(a::Measurement) = result(cos(a.val), -sin(a.val), a)
や
-(a::Measurement, b::Measurement) = result(a.val - b.val, (1, -1), (a, b))
のように実装されています。
より詳しくはDefining Methods for Mathematical Operations参照してください。
まとめ
-
Measurements.jlは誤差を含んだ型を提供し、線形誤差伝播を自動化してくれるパッケージ。 - 他のパッケージともよく調和する。
- 連鎖律を用いて固有な測定値に還元することでうまく実装されてる
実験データ解析に便利なのでぜひ使ってみてください。
あと統計周りでも使えるようになるといいですね。
Qiitaのインライン数式、subscriptの_が italic の_に解釈されてうまく組めない。