DeepLearningの概要→実装まで

はじめに

この記事はDeep Learningに関する自分用メモです。
説明が怪しいこともあるし、詳しく説明してなかったりするけど堪忍。

この記事の想定読者

Deep Learningどころかプログラミング何も知らない人

AI、機械学習、Deep Learningの関係

これとかこれとかみてくれ（3分で読める）

教師あり学習と教師なし学習

どっちも機械学習のひとつ。

教師あり学習

教師あり学習は、入力$x$に対して、$y$という「答え」を出力（予測）させるための学習。
学習の時点で、「この条件○○だったら答えは△△だ」というのを学習させる。
だから$x$と$y$をセットで学習させることになる。
端的に言えば、"ラベル"がある学習。

（例）

• 部屋の広さ$x_{1}$：10畳
• 寝室の数$x_{2}$：0
• 最寄り駅までの距離$x_{3}$：徒歩10分
• $y$：家賃8万円

答えを覚えたり法則を覚えたりして、それを応用してテストを解けるようにする、いわゆる"テスト勉強"のイメージかな。

教師なし学習

教師あり学習に対して教師なし学習は、"ラベル"がない学習。
とりあえずいろんな特徴量を持つデータ($x$)だけをぶっこんで、なにかしらの推測をさせる。
クラスタリングとか主成分分析とかベクトル量子化とか自己組織化マップについては他の記事をみてくれ。（wikipediaのリンクを雑に貼っておく）

（例）

• 大量の購買データから、客層（性別/年齢/人数/構成）、状況（季節/時間帯/天候）、購入対象(ジャンル/メーカー/価格/数/買い合わせ)の傾向をつかむ
• 大量のブログ記事アクセスデータから、読者(性別/年齢)、記事の特徴(文字数/タグ/画像の数/投稿時間)、アクセス方法(時間帯/OS/ブラウザ)へのアクセスの傾向をつかむ

答えがない中でたくさんのデータを集めて、自分なりに分類してみたり抽象的な法則を見つけたりする、いわゆる"研究"のイメージに近い。

Deep Learning

Deep：層が深い
Learning：学習
ここでいう"層が深い"というのは、畳み込みニューラルネットワーク(CNN)の畳み込み層が深い（層が多い）という意味。
そしてCNNは、ニューラルネットワークのうち「"畳み込み層"がある版」です。強いやつ。
CNNのCは、Comvolution（畳み込み）という意味。
Cを含むNNなので、CNN。
ちなみに格ゲーとかのコンボは、Combination（組み合わせ）なので間違えないように。

ニューラルネットワークとは

ニューラルネットワークの中では、入力$x$を元に、"なにかしらの計算"をして、$y$を出力する。
（例）住宅の条件$x$を元に、家賃$y$を計算（予測）する。
したがって、ニューラルネットワークも教師あり学習に含まれる。
入力xは"特徴量"と呼ばれ、たいていの場合、複数の要素で成り立つ。

（例）

• $x_{1}$：部屋の広さ
• $x_{2}$：寝室の数
• $x_{3}$：最寄り駅までの距離
• $y$：家賃

この$x$をもとに"なにかしらの計算"をして$y$を出力する。それは
$y = x_{1} + x_{2} + x_{3}$　かもしれませんし、
$y = \frac{x_{1}x_{2}}{x_{3}}$　かもしれませんし、
$y = x_{1}^{x_{2} - x_{3}}$　かもしれません。

ちなみにニューラルはneuralで、neuron（神経）という意味。
"なにかしらの計算"というのが、かけ算やたし算などの様々な計算を組み合わせて成り立っており、それを図にするとまるで神経細胞のようにごちゃごちゃになるから、そう呼ばれている。（あってる？）
（そもそも実際の細胞での信号の伝達もほぼ同じことをしてるっぽい（適当））

入力データについて

ちなみに入力$x$には大きく「構造化データ」「非構造化データ」の２つがある。

• 構造化データ：表データなど。
  • $x_{1}$:部屋の広さ
• 非構造化データ：音声、画像、テキストなど。
  • 画素や語が１つの入力になる。

Deep Learningが活躍できる場

データ量がじゅうぶんに多い領域。（10,000とか）
データ量が少ない領域ではDeep Learningの強みは活かされず、他のソリューションの方がいい結果を出せる場合もある。

二値分類

バイナリ分類とか呼んだりする。ある画像を

• 猫[1]
• 猫ではない[0]

と判断するとか。

• 画像データ$x$
  • 画像サイズを　$64 * 64$　とすると、
  • 色の要素であるRGBそれぞれに　$64 * 64$　の情報があるので、
  • 画像データ1枚の次元　$n = 3 * 64 * 64(次元)$　となる。
• 教師ラベル$y$
  • $1$
  • $0$

画像データ数を$m$とすると、入力ベクトル$X$、出力ベクトル$Y$の大きさは

• $ X = [n * m]$
  $[13,254,198,172,201,89,...,122]（64*64個）$とかが$3$枚。が、$m$個

• $ Y = [1 * m]$
  $[1]$とか$[0]$が$m$個

ロジスティクス回帰

ロジスティクス回帰：二値分類で使われるアルゴリズム。
非線形解析の1つで、以下の式で表される。
目的関数は、今回の例で言えば出力$y$。（別に$f(x)$と書いてもいい。）

• 線形解析：目的関数 $z = w_{1}x_{1}+w_{2}x_{2}+...w_{n}x_{n}+b$（線形）
• 非線形解析：目的関数 $z = $（線形じゃないなにか）
  • （例）ロジスティクス回帰：目的関数 $z = \frac{1}{1+exp(-(w_{1}x_{1}+w_{2}x_{2}+...w_{n}x_{n}+b))}$

ここで、

• 次元$n_{x}$のベクトル$w$
• 実数$b$

がパラメータ。
$z = \frac{1}{1+exp(-(w_{1}x_{1}+w_{2}x_{2}+...w_{n}x_{n}+b))}$の部分は一般にシグモイド関数と呼ばれ、$σ(x)=\frac{1}{1+exp(-x)}$で表される。
シグモイド関数を用いることで、値を確率に落とし込むことができる。

• $σ(x)=\frac{1}{1+exp(-x)}$において、$x=-∞$のとき、$σ(-∞)=0$に収束する。
• $σ(x)=\frac{1}{1+exp(-x)}$において、$x=+∞$のとき、$σ(+∞)=1$に収束する。

0~1の間に落とし込めている＝確率に落とし込めているのです。
（これ以上は言及しない）

損失関数

$y_{valid}$（出力、推論結果） = $σ(w^{T}x + b)$
『教師あり学習』の項目で述べた通り、学習のモチベーションは、「こうあってほしい正解$y_{train}$」に近づけることになる。
そこで導入されるのが損失関数という考え方である。
学習を進める$≒$損失関数$L$を小さくしていくこと、と思っていただいて差し支えない。

二乗和誤差

二乗和誤差では、損失関数$L$を以下で定義する。
$$L = \frac{1}{2}(y_{valid}-y_{train})^{2}$$
これは直感的にわかりやすい。
正解と推測結果の差を小さくしていくことが、そのまま損失関数を小さくすることだからだ。

交差エントロピー誤差

割愛します。

ロジスティクス回帰に置ける損失関数

「損失関数$L$を小さくしたいんだな」ってことをわかってもらえたところで、ロジスティクス回帰においては、損失関数$L$を二乗和誤差ではなく、次のように定義している。
$$L = -( y_{train}logy_{valid}+(1-y_{train})log(1-y_{valid}))$$

一見キモいが、実は以下の2点から、「$L$を小さくしたい」$=$「$y_{valid}$を$y_{train}$に近づけたい」であることをおわかりいただけると思う。

• $y_{train}$が$1$のとき
  • $L = -logy_{valid}$
  • 「$L$を$0$にしたい」→「$y_{valid}$を$1$($=y_{train}$)に近づけたい」
• $y_{train}$が$0$のとき
  • $L = -log(1-y_{valid})$
  • 「$L$を$0$にしたい」→「$y_{valid}$を$0$($=y_{train}$)に近づけたい」

コスト関数

コスト関数$J$は、損失関数の平均をとる。
平均というのは、データ数$m$の平均である。
$$J=\frac{1}{m}\sum_{i=1}^{m} L(y_{valid}^{i},y_{train}^{i})$$
$$=-\frac{1}{m}\sum_{i=1}^{m} [y_{train}^{i}logy_{valid}^{i}+(1-y_{train}^{i})log(1-y_{valid}^{i})]$$
1枚目からm枚目までの全データについて$L$を計算し、その平均をとるのである。
学習中は、コスト関数の値を計算し、コストを最小にする$W$と$b$を探していくことになる。

※会話で「ロスは下がっているから学習は進んでいるはず」などという時には、厳密にはこの「コスト関数が下がっている」ということを意味していると解釈する。コスト関数は損失関数の平均だからね。実質同じだよ。

確率的勾配降下法

微分を使って、コスト関数が一番小さくなることを目指す考え方。
ざっくり言えば、

1. 微分を用いて「ある点からどの方向に進めば一番勾配が0に近づくか」を計算し、その方向に少しだけ移動する。
2. 繰り返し
   これで、勾配が変化しなくなったら、コスト関数が限りなく小さくなった＝収束＝学習完了。
   これは、コスト関数が凸関数だからこそできること。
   詳細は割愛する。
   結論としては、$w$と$b$の更新は以下の式に基づいて進んでいく。

$w←w-α（学習率）*\frac{dJ(w,b)}{dw}$

$b←b-α（学習率）*\frac{dJ(w,b)}{db}$

計算グラフ

『ニューラルネットワーク』のところで述べた通り、ニューラルネットワークの内部で行われている"なにかしらの計算"は、たし算やかけ算を神経回路のように組み合わせて行われている。
そしてその1つ1つの計算は、「計算グラフ」というものが元になっている。
ロジスティクス回帰でやっていることは、
$$x_{1}, w_{1}, x_{2}, w_{2}, b → z = x_{1}w_{1}+x_{2}w_{2}+b → a = σ(z) → L(a,y)$$
目的関数$z$をシグモイド関数で確率$a$に落とし込み、損失関数$L$を計算する。
$$w←w-α（学習率）*\frac{dJ(w,b)}{dw}$$

$$b←b-α（学習率）*\frac{dJ(w,b)}{db}$$
$L$の、各パラメータごとの微分を求めて、ちょっとずつ移動させて$L$を減らしていく。

計算グラフでの微分

$\frac{dJ}{da}$は、$a$を微小量変化させた時の$J$の変化量のこと。
コード上では、$\frac{dJ}{da}$のことを省略してdaと書く。
ちなみに、重要なことをしれっと書くと、$\frac{dL}{dz}=\frac{dL}{da}\frac{da}{dz}$は以下のようになる。
$$\frac{dL}{dz}=a-y$$

ロジスティクス回帰での勾配降下

計算グラフを逆伝播していく。

大量データに対する勾配降下

データ数$m$の場合、i=1→mまでのforループを回すことになります。
ですが、pythonではnumpyを使うことによって行列での計算ができ、これを一行で計算できたりします。
ここでは理論の話をしたいので、それがいかに早いか、具体的にどういうコードを書くかは割愛します。

関数の実装

シグモイド関数

$s = \frac{1}{1+exp^{-x}}$

import numpy as np

def sigmoid(x): # シグモイド関数を計算するやつ
    s = 1 / (1+np.exp(-x))

    return s

シグモイド関数の微分

$s' = s(1-s)$

def sigmoid_derivative(x): # シグモイド関数の微分を計算するやつ
    s = 1 / (1+ np.exp(-x))
    ds = s*(1-s)

１列に並べる

    return ds
def image2vector(image): # RGBとかを１列に並べるやつ    
    v = image.reshape((image.shape[0]*image.shape[1]*image.shape[2]),1)
    
    return v

正規化

$x = \frac{x}{||x||}$

def normalizeRows(x): # 正規化
    x_norm = np.linalg.norm(x, axis =1, keepdims=True) # 二乗和の平方根
    x = x / x_norm

    return x

ソフトマックス関数

$s = [\frac{exp^{x1}}{\sum_{j} exp^{xj}}, \frac{exp^{x2}}{\sum_{j} exp^{xj}}, ... \frac{exp^{xn}}{\sum_{j} exp^{xj}}]$

def softmax(x): # ソフトマックス    
    x_exp = np.exp(x)
    x_sum = np.sum(x_exp, axis=1, keepdims=True)    
    s = x_exp / x_sum
    
    return s

損失関数

$L_{1}(\hat{y},y) = \sum_{i=0}^{m}|y^{i}-\hat{y}^{i}|$
$L_{2}(\hat{y},y) = \sum_{i=0}^{m}(y^{i}-\hat{y}^{i})^{2}$

def L1(yhat, y):
    loss = np.sum(abs(y-yhat))
    
    return loss

def L2(yhat, y):
    loss = np.sum(np.dot(abs(y-yhat),abs(y-yhat)))

    return loss

簡単な画像認識モデルの実装

必要なパッケージのインストール、画像のインストール

import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
%matplotlib inline

train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
# x:猫の画像、猫じゃない画像
# y:1,0(1が猫、0が猫じゃない)

0.データセットの情報の確認

やりたいこと：学習データセット、推論データセットのサンプル数、ピクセル数を確認する。

m_train = len(train_set_x_orig) # 209
m_test = len(test_set_x_orig) # 50
num_px = train_set_x_orig.shape[1] # 64

1.１列に並べる

やりたいこと：64x64x3(RGB)ピクセルのデータを、１列に並べる。

train_set_x_flatten = train_set_x_orig.reshape((num_px*num_px*3),m_train) # (12288, 209) = (64x64x3, 209)
test_set_x_flatten = test_set_x_orig.reshape((num_px*num_px*3),m_test) # (12288, 50)

画像データは例外なく、1つのピクセルがRGB 0〜255の3要素からなるベクトルで構成されている。

train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255

2.シグモイド関数

やりたいこと：シグモイド関数の定義。

def sigmoid(z):
      s = 1/(1+(np.exp(-z)))    
    return s

3.パラメータの初期化

やりたいこと：パラメータ（重み、バイアス）の初期化。

def initialize_with_zeros(dim):    
    w = np.zeros([dim,1])  # [[ 0.][ 0.]]
    # w = np.zeros(dim)  # [ 0. 0. ]
    b = 0

    assert(w.shape == (dim, 1))
    assert(isinstance(b, float) or isinstance(b, int))
    
    return w, b

4.propagation(伝播)

やりたいこと：forward方向でコストの計算、back方向で勾配を計算。
forward:
$A = σ(w^{T}X + b) = (a^{(1)}, a^{(2)}, ... a^{(m-1)},a^{(m)})$
$J = - \frac{1}{m}\sum_{i=1}^{m} y^{(i)} log(a^{(i)}) + (1-y^{(i)})log(1-a^{(i)})$
back:
$\frac{∂J}{∂w}=\frac{1}{m}X(A-Y)^{T}$
$\frac{∂J}{∂b}=\frac{1}{m}\sum_{i=1}^{m}(a^{(i)}-y^{(i)})$

def propagate(w, b, X, Y):
    m = X.shape[1]
    
    # FORWARD PROPAGATION (FROM X TO COST)
    A = sigmoid(np.dot(w.T, X)+b)
    cost = -1/m*(np.dot(Y,np.log(A.T))+np.dot((1-Y),np.log(1-A.T)))
    
    # BACKWARD PROPAGATION (TO FIND GRAD)
    dw = 1/m*np.dot(X,(A-Y).T)
    db = 1/m*np.sum(A-Y)

    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    grads = {"dw": dw,
             "db": db}
    
    return grads, cost

5.最適化

やりたいこと：勾配降下を利用して、パラメータを更新する。
$ w = w - αdw $
$ b = b - αdb $

# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
    costs = []
    for i in range(num_iterations):
        
        # Cost and gradient calculation (≈ 1-4 lines of code)
        grads, cost =  propagate(w, b, X, Y)　＃さっき定義した関数
        
        # Retrieve derivatives from grads
        dw = grads["dw"]
        db = grads["db"]
        
        # update rule (≈ 2 lines of code)
        w = w - learning_rate*dw
        b = b - learning_rate*db
        
        # Record the costs
        if i % 100 == 0:
            costs.append(cost)
        
        # Print the cost every 100 training iterations
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
    
    params = {"w": w,
              "b": b}
    
    grads = {"dw": dw,
             "db": db}
    
    return params, grads, costs

6.推論の関数

やりたいこと：学習した重み$w$とバイアス$b$を用いて、推論データセットに対して推論する($\hat{Y}$を求める)ための関数を実装する。
$ \hat{Y}=A=σ(w^{T}X+b) $
Aを計算して、各要素が「0.5以下なら0（=猫でない）、0.5より大きかったら1（=猫である）」とする。

# GRADED FUNCTION: predict
def predict(w, b, X):
    m = X.shape[1]
    Y_prediction = np.zeros((1,m))
    w = w.reshape(X.shape[0], 1)
    
    A = sigmoid(np.dot(w.T,X)+b)

# Aの値（確率）を、判断Y（猫か、そうでないか）に落とし込みます。
    for i in range(A.shape[1]):
        Y_prediction = (A >= 0.5).astype(np.int)
    assert(Y_prediction.shape == (1, m))
    
    return Y_prediction

例：

print(A) # ([ 0.620192 0.309815 0.509817 ])
print(Y_prediction) # ([1 0 1])

7.モデル作成

やりたいこと：上記で実装してきた関数を、1つのモデルへと統合する。

# GRADED FUNCTION: model

def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):    
    
    # パラメータの初期化
    w, b = initialize_with_zeros(12288)

    # 勾配降下
    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
    
    # "parameters"ディクショナリからwとbを取り戻します。
    w = parameters["w"]
    b = parameters["b"]
    
    # テストデータ、訓練データに対して予測します。
    Y_prediction_test = predict(w, b, X_test)
    Y_prediction_train = predict(w, b, X_train)

    # テストデータ、訓練データのエラーをprintします。
    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
    
    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}
    
    return d

d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

# 学習曲線とコストのプロット
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

# 各学習率による学習曲線
learning_rates = [0.008, 0.005, 0.003, 0.001]
models = {}
for i in learning_rates:
    print ("learning rate is: " + str(i))
    models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
    print ('\n' + "-------------------------------------------------------" + '\n')

for i in learning_rates:
    plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()

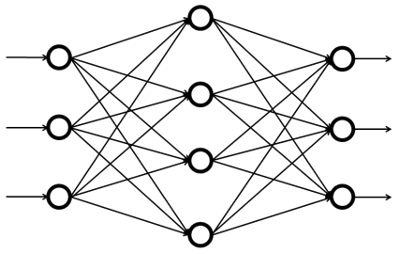
ニューラルネットワーク

ロジスティクス回帰：隠れ層がなく、行う計算は出力層の$z=wx+b$のみ。
ニューラルネットワーク：隠れ層があり、層ごとにそれぞれユニットが複数あり、複数の計算を行っている。この隠れ層が多いものを"ディープなニューラルネットワーク"という意味を込めて"ディープラーニング"と呼んでいる。

1. ニューラルネットワークの構造決定（ユニットの数、隠れ層の数など）
2. モデルのパラメータを初期化（w,b)
3. ループ

• 前方伝播
• ロスを計算する
• 後方伝播を計算して勾配降下を求める
• パラメータを更新する

###パラメータを初期化

    def initialize_parameters(n_x, n_h, n_y):
    
    W1 = np.random.randn(n_h,n_x) * 0.01
    b1 = np.zeros([n_h,1])
    W2 = np.random.randn(n_y,n_h) * 0.01
    b2 = np.zeros([n_y,1])
    
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    return parameters

前方伝播

def forward_propagation(X, parameters):

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]  

    Z1 = np.dot(W1,X)+b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1)+b2
    A2 = sigmoid(Z2)
    
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

ロスを計算する

    def compute_cost(A2, Y, parameters):

    m = Y.shape[1] # number of example

    logprobs = np.multiply(np.log(A2),Y)+np.multiply(np.log(1-A2),1-Y)
    cost = -1/m*np.sum(logprobs)
    
    cost = float(np.squeeze(cost))

    assert(isinstance(cost, float))
    
    return cost

後方伝播を計算して勾配降下を求める

    def backward_propagation(parameters, cache, X, Y):

    m = X.shape[1]

    W1 = parameters["W1"]
    W2 = parameters["W2"]
        
    A1 = cache["A1"]
    A2 = cache["A2"]

    dZ2 = A2 - Y
    dW2 = 1/m*np.dot(dZ2,np.transpose(A1))
    db2 = 1/m*np.sum(dZ2, axis = 1, keepdims =True)
    dZ1 = np.dot(np.transpose(W2),dZ2) * (1-np.power(A1,2))
    dW1 = 1/m*np.dot(dZ1,np.transpose(X))
    db1 = 1/m*np.sum(dZ1, axis = 1, keepdims =True)
    
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

パラメータを更新する

    def update_parameters(parameters, grads, learning_rate = 1.2):

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

ニューラルネットワークの実装

    def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):

    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]

    parameters = initialize_parameters(n_x, n_h, n_y)

    for i in range(0, num_iterations):
                 
        # 前方伝播
　　　　 A2, cache = forward_propagation(X, parameters)

        # コスト関数の計算
        cost = compute_cost(A2, Y, parameters)
 
        # 後方伝播
        grads = backward_propagation(parameters, cache, X, Y)
 
        # 勾配降下によるパラメータ更新
        parameters = update_parameters(parameters, grads)
                
        # 1000イテレートごとにコストを記述
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters

推論

def predict(parameters, X):
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)

かゆい
うま
（日記はここで途切れている）