import sympy as sp
# シンボリック変数の定義
t, s = sp.symbols('t s')
a, b, c, d = sp.symbols('a b c d')
A = sp.Matrix([[a, b], [c, d]])
I = sp.eye(2)
# ラプラス変換を用いた状態遷移行列の計算
Phi_s_laplace = (s * I - A).inv()
Phi_t_laplace = sp.inverse_laplace_transform(Phi_s_laplace, s, t)
# 対角化を用いた状態遷移行列の計算
P, D = A.diagonalize()
Phi_t_diag = P * sp.exp(D * t) * P.inv()
# 結果の表示
print("ラプラス変換を用いた状態遷移行列:")
sp.pprint(Phi_t_laplace)
print("\n対角化を用いた状態遷移行列:")
sp.pprint(Phi_t_diag)
import numpy as np
import scipy.linalg
import matplotlib.pyplot as plt
# システムパラメータの設定
m = 0.2 # 振子の質量 (kg)
M = 0.5 # カートの質量 (kg)
L = 0.3 # 振子の長さ (m)
g = 9.81 # 重力加速度 (m/s^2)
d = 0.1 # 摩擦係数
# 状態空間モデルの行列
A = np.array([[0, 1, 0, 0],
[0, -d/M, m*g/M, 0],
[0, 0, 0, 1],
[0, -d/(M*L), (M+m)*g/(M*L), 0]])
B = np.array([[0],
[1/M],
[0],
[1/(M*L)]])
C = np.array([[1, 0, 0, 0],
[0, 0, 1, 0]])
D = np.array([[0],
[0]])
# LQRの重み行列
Q = np.diag([10, 1, 10, 1])
R = np.array([[0.1]])
# リカッチ方程式を解いてLQRゲインを計算
X = np.matrix(scipy.linalg.solve_continuous_are(A, B, Q, R))
K = np.matrix(scipy.linalg.inv(R) * (B.T * X))
# シミュレーションの設定
dt = 0.01 # 時間ステップ (s)
T = 10.0 # シミュレーション時間 (s)
t = np.arange(0, T, dt)
# 初期状態
x = np.array([[0.1], # 初期カート位置 (m)
[0.0], # 初期カート速度 (m/s)
[0.1], # 初期振子角度 (rad)
[0.0]]) # 初期振子角速度 (rad/s)
# シミュレーションの実行
x_history = []
for _ in t:
u = -K * x # 制御入力
x_dot = A * x + B * u # 状態の微分
x = x + x_dot * dt # 状態の更新
x_history.append(x.A1) # 状態履歴の保存
x_history = np.array(x_history)
# 結果のプロット
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(t, x_history[:, 0])
plt.ylabel('Cart Position (m)')
plt.grid(True)
plt.subplot(4, 1, 2)
plt.plot(t, x_history[:, 1])
plt.ylabel('Cart Velocity (m/s)')
plt.grid(True)
plt.subplot(4, 1, 3)
plt.plot(t, x_history[:, 2])
plt.ylabel('Pendulum Angle (rad)')
plt.grid(True)
plt.subplot(4, 1, 4)
plt.plot(t, x_history[:, 3])
plt.ylabel('Pendulum Angular Velocity (rad/s)')
plt.xlabel('Time (s)')
plt.grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import place_poles, StateSpace, lti, step, lsim
# Define the first-order lag system
a = 1.0 # Time constant
b = 1.0 # Gain
# State-space representation
A = np.array([[-a]])
B = np.array([[b]])
C = np.array([[1.0]])
D = np.array([[0.0]])
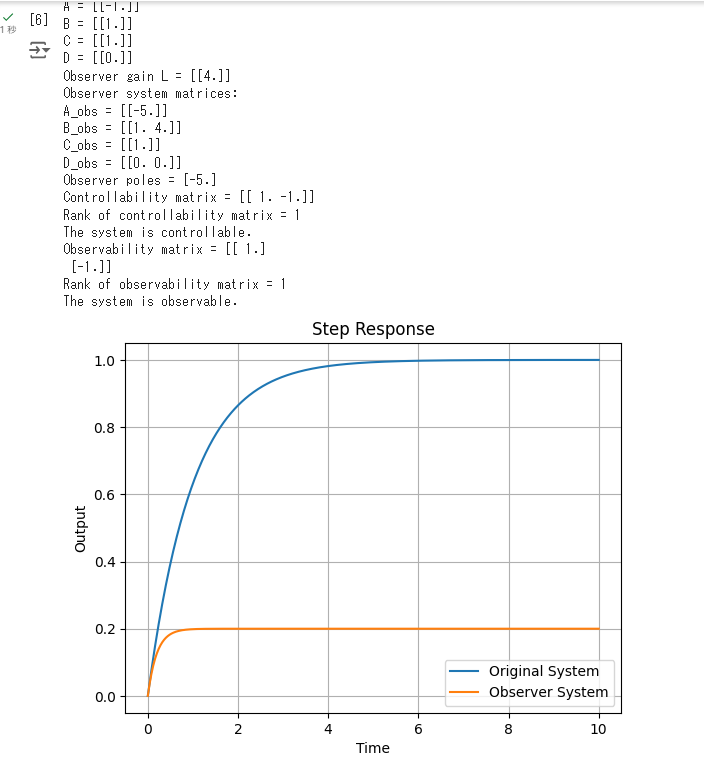
print("State-space representation:")
print("A =", A)
print("B =", B)
print("C =", C)
print("D =", D)
# Define observer pole
observer_pole = -5.0 # Desired observer pole
# Calculate observer gain L
L = place_poles(A.T, C.T, [observer_pole]).gain_matrix.T
print("Observer gain L =", L)
# Observer system matrices
A_obs = A - L @ C
B_obs = np.hstack([B, L])
C_obs = C
D_obs = np.zeros((C.shape[0], B_obs.shape[1])) # Adjusting the shape of D_obs
print("Observer system matrices:")
print("A_obs =", A_obs)
print("B_obs =", B_obs)
print("C_obs =", C_obs)
print("D_obs =", D_obs)
# Calculate the poles of the observer system
observer_poles = np.linalg.eigvals(A_obs)
print("Observer poles =", observer_poles)
# Check controllability
controllability_matrix = np.hstack([B, A @ B])
rank_controllability = np.linalg.matrix_rank(controllability_matrix)
print("Controllability matrix =", controllability_matrix)
print("Rank of controllability matrix =", rank_controllability)
if rank_controllability == A.shape[0]:
print("The system is controllable.")
else:
print("The system is not controllable.")
# Check observability
observability_matrix = np.vstack([C, C @ A])
rank_observability = np.linalg.matrix_rank(observability_matrix)
print("Observability matrix =", observability_matrix)
print("Rank of observability matrix =", rank_observability)
if rank_observability == A.shape[0]:
print("The system is observable.")
else:
print("The system is not observable.")
# Define time vector for simulation
t = np.linspace(0, 10, 500)
# Original system step response
original_system = lti(A, B, C, D)
t, y = step(original_system, T=t)
# Observer system step response
observer_system = StateSpace(A_obs, B_obs, C_obs, D_obs)
U = np.hstack([np.ones((t.size, 1)), np.zeros((t.size, 1))])
_, y_obs, _ = lsim(observer_system, U=U, T=t)
# Plot the step response of the original system and the observer
plt.figure()
plt.plot(t, y, label='Original System')
plt.plot(t, y_obs, label='Observer System')
plt.xlabel('Time')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.title('Step Response')
plt.show()
import numpy as np
import scipy.linalg
import scipy.signal
import matplotlib.pyplot as plt
# システムパラメータの定義
m = 0.1 # 振子の質量(kg)
M = 1.0 # カートの質量(kg)
L = 1.0 # 振子の長さ(m)
g = 9.81 # 重力加速度(m/s^2)
# システム行列の定義
A = np.array([[0, 1, 0, 0],
[0, 0, -(m * g) / M, 0],
[0, 0, 0, 1],
[0, 0, (M + m) * g / (M * L), 0]])
B = np.array([[0],
[1 / M],
[0],
[-1 / (M * L)]])
C = np.array([[1, 0, 0, 0]])
D = np.array([[0]])
# 可制御性行列
def controllability_matrix(A, B):
n = A.shape[0]
C = B
for i in range(1, n):
C = np.hstack((C, np.linalg.matrix_power(A, i).dot(B)))
return C
# 可観測性行列
def observability_matrix(A, C):
n = A.shape[0]
O = C
for i in range(1, n):
O = np.vstack((O, C.dot(np.linalg.matrix_power(A, i))))
return O
# 可制御性の確認
Ctrb = controllability_matrix(A, B)
if np.linalg.matrix_rank(Ctrb) == A.shape[0]:
print("システムは可制御です。")
else:
print("システムは可制御ではありません。")
# 可観測性の確認
Obsv = observability_matrix(A, C)
if np.linalg.matrix_rank(Obsv) == A.shape[0]:
print("システムは可観測です。")
else:
print("システムは可観測ではありません。")
# LQRによるフィードバックゲインの計算
Q = np.diag([1, 1, 10, 100])
R = np.array([[1]])
K, _, _ = scipy.linalg.lqr(A, B, Q, R)
print("フィードバックゲイン K:", K)
# 閉ループシステムの極
A_cl = A - B.dot(K)
poles_cl = np.linalg.eigvals(A_cl)
print("閉ループシステムの極:", poles_cl)
# 閉ループシステムの伝達関数
sys_cl = scipy.signal.StateSpace(A_cl, B, C, D)
tf_cl = scipy.signal.TransferFunction(*scipy.signal.ss2tf(A_cl, B, C, D))
# ボード線図のプロット
w, mag, phase = scipy.signal.bode(tf_cl)
plt.figure()
plt.subplot(2, 1, 1)
plt.semilogx(w, mag)
plt.title('Bode Diagram')
plt.ylabel('Magnitude (dB)')
plt.subplot(2, 1, 2)
plt.semilogx(w, phase)
plt.ylabel('Phase (degrees)')
plt.xlabel('Frequency (rad/s)')
plt.show()
import numpy as np
import scipy.linalg
import matplotlib.pyplot as plt
from scipy.signal import place_poles
# システムパラメータ
l = 1.0 # 振子の長さ
g = 9.81 # 重力加速度
# システム行列
A = np.array([[0, 1],
[2*g/l, 0]])
B = np.array([[0],
[-1/(l/2)]])
C = np.array([[1, 0]])
D = np.array([[0]])
# 状態フィードバックゲインKの計算 (LQR)
Q = np.eye(2)
R = np.array([[1]])
K, _, _ = scipy.linalg.lqr(A, B, Q, R)
# オブザーバーの極配置
desired_poles = np.array([-2, -3])
L = place_poles(A.T, C.T, desired_poles).gain_matrix.T
# シミュレーションパラメータ
dt = 0.01
t = np.arange(0, 10, dt)
# 初期状態
x = np.array([[0.1],
[0.0]]) # 初期の角度と角速度
x_hat = np.array([[0.0],
[0.0]]) # 初期推定値
x_history = []
u_history = []
for i in range(len(t)):
# 制御入力の計算
u = -K @ x_hat
u_history.append(u[0, 0])
# システムの次の状態の計算
x_dot = A @ x + B @ u
x = x + x_dot * dt
x_history.append(x.flatten())
# オブザーバの次の推定状態の計算
y = C @ x
y_hat = C @ x_hat
x_hat_dot = A @ x_hat + B @ u + L @ (y - y_hat)
x_hat = x_hat + x_hat_dot * dt
x_history = np.array(x_history)
u_history = np.array(u_history)
# 結果のプロット
plt.figure(figsize=(10, 8))
plt.subplot(3, 1, 1)
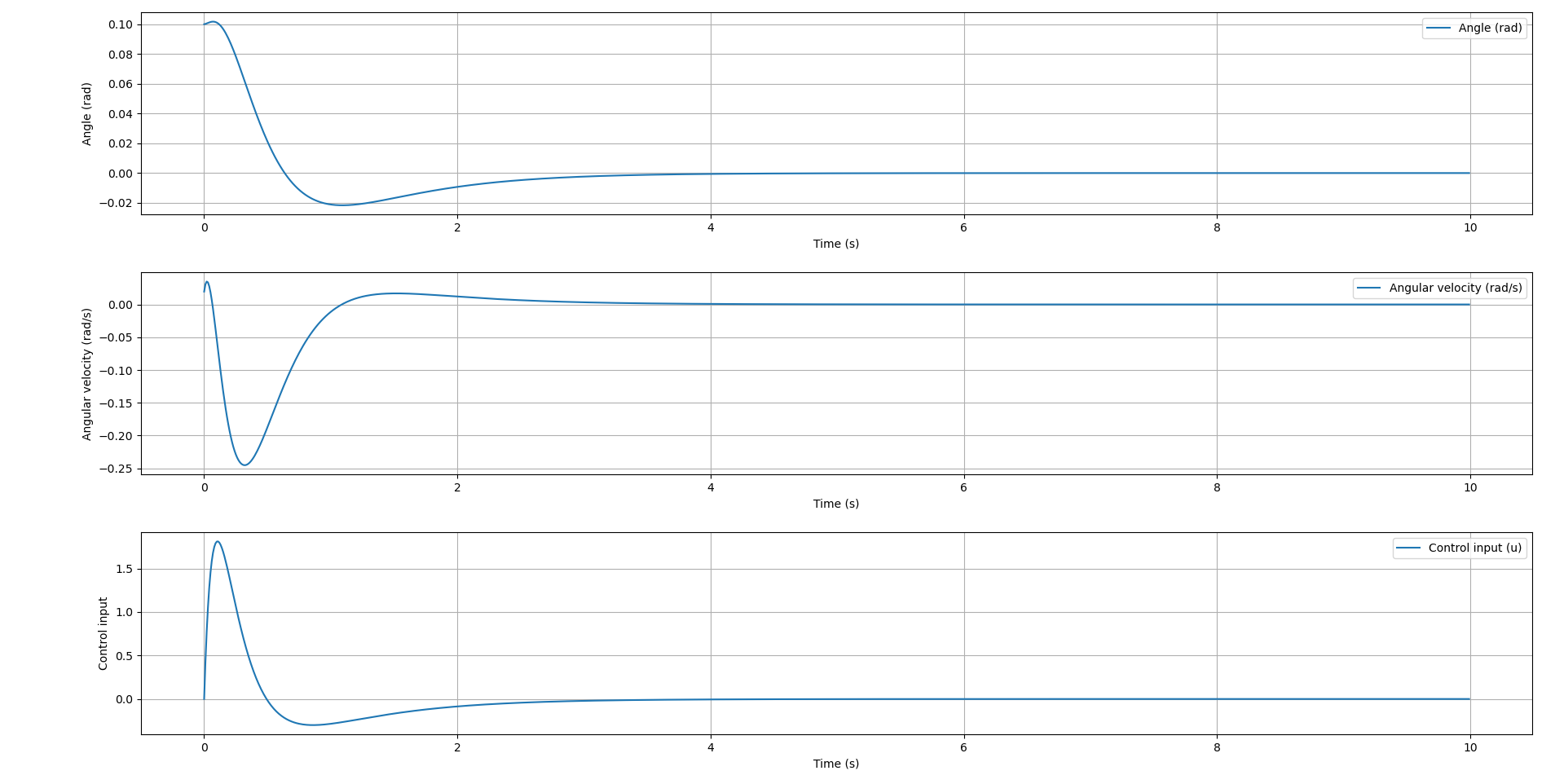
plt.plot(t, x_history[:, 0], label='Angle (rad)')
plt.xlabel('Time (s)')
plt.ylabel('Angle (rad)')
plt.legend()
plt.grid()
plt.subplot(3, 1, 2)
plt.plot(t, x_history[:, 1], label='Angular velocity (rad/s)')
plt.xlabel('Time (s)')
plt.ylabel('Angular velocity (rad/s)')
plt.legend()
plt.grid()
plt.subplot(3, 1, 3)
plt.plot(t, u_history, label='Control input (u)')
plt.xlabel('Time (s)')
plt.ylabel('Control input')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
import sympy as sp
# シンボリック変数の定義
t, s = sp.symbols('t s')
a, b, c, d = 1, 2, 3, 4 # ここに具体的な値を代入
A = sp.Matrix([[a, b], [c, d]])
I = sp.eye(2)
# ラプラス変換を用いた状態遷移行列の計算
Phi_s_laplace = (s * I - A).inv()
Phi_t_laplace = sp.inverse_laplace_transform(Phi_s_laplace, s, t)
# 対角化を用いた状態遷移行列の計算
P, D = A.diagonalize()
Phi_t_diag = P * sp.exp(D * t) * P.inv()
# 結果の表示(TeX記法)
print("ラプラス変換を用いた状態遷移行列:")
print(sp.latex(Phi_t_laplace))
print("\n対角化を用いた状態遷移行列:")
print(sp.latex(Phi_t_diag))
import numpy as np
import scipy.linalg
import scipy.signal as signal
import matplotlib.pyplot as plt
# Transfer function coefficients
a, b, c = 1.0, 2.0, 1.0 # Example values: a=1, b=2, c=1
# Define the transfer function
num = [1]
den = [a, b, c]
system = signal.TransferFunction(num, den)
# Convert to state-space representation
A, B, C, D = signal.tf2ss(num, den)
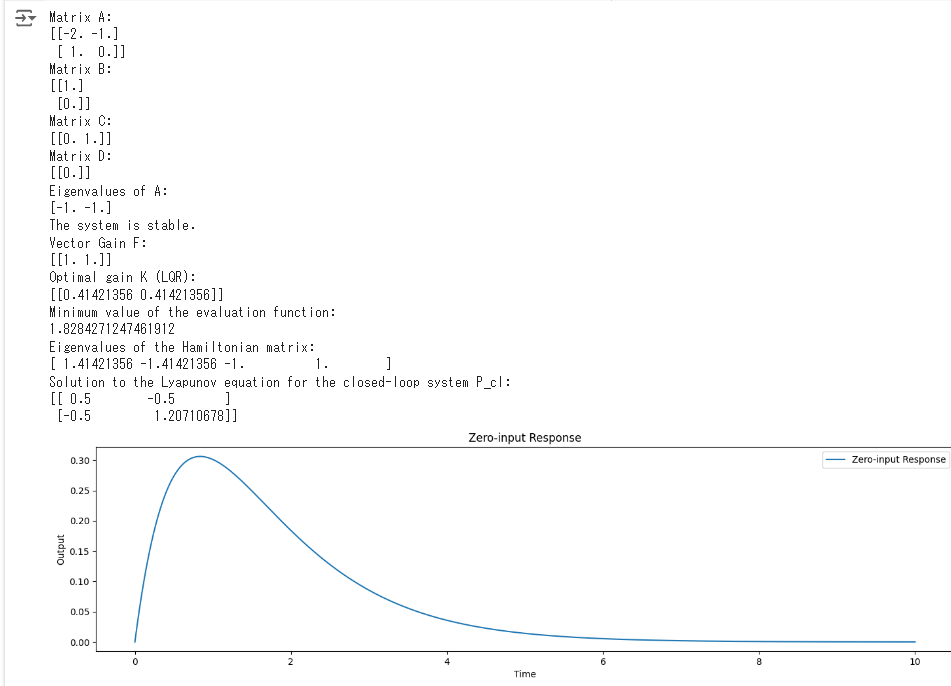
print("Matrix A:")
print(A)
print("Matrix B:")
print(B)
print("Matrix C:")
print(C)
print("Matrix D:")
print(D)
# Check if the matrix is regular (diagonalization)
eigvals, eigvecs = np.linalg.eig(A)
print("Eigenvalues:")
print(eigvals)
print("Eigenvectors:")
print(eigvecs)
# Solve the Lyapunov equation
Q = np.eye(A.shape[0])
P = scipy.linalg.solve_continuous_lyapunov(A, -Q)
print("Solution to the Lyapunov equation P:")
print(P)
# Check controllability
controllability_matrix = np.hstack([B, np.dot(A, B)])
print("Controllability Matrix:")
print(controllability_matrix)
controllable = np.linalg.matrix_rank(controllability_matrix) == A.shape[0]
print(f"The system is {'controllable' if controllable else 'not controllable'}.")
# Check observability
observability_matrix = np.vstack([C, np.dot(C, A)])
print("Observability Matrix:")
print(observability_matrix)
observable = np.linalg.matrix_rank(observability_matrix) == A.shape[0]
print(f"The system is {'observable' if observable else 'not observable'}.")
# Time settings for simulation
t = np.linspace(0, 10, 1000)
# Initial state
x0 = [1, 0] # Example initial state [1, 0]
# Zero-input response
_, y_zero_input, x_zero_input = signal.lsim((A, B, C, D), U=0, T=t, X0=x0)
# Zero-state response
u = np.ones_like(t)
_, y_zero_state, x_zero_state = signal.lsim((A, B, C, D), U=u, T=t, X0=0)
# Plotting
plt.figure(figsize=(14, 8))
# Plot zero-input response
plt.subplot(2, 1, 1)
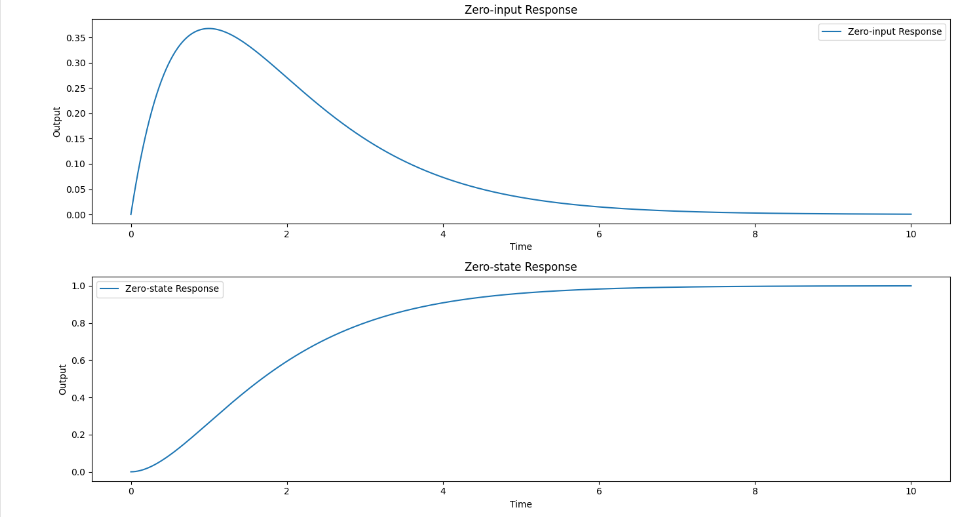
plt.plot(t, y_zero_input, label='Zero-input Response')
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Zero-input Response')
plt.legend()
# Plot zero-state response
plt.subplot(2, 1, 2)
plt.plot(t, y_zero_state, label='Zero-state Response')
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Zero-state Response')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import scipy.linalg
import scipy.signal as signal
import matplotlib.pyplot as plt
# Transfer function coefficients
a, b, c = 1.0, 2.0, 1.0 # Example values: a=1, b=2, c=1
# Define the transfer function
num = [1]
den = [a, b, c]
system = signal.TransferFunction(num, den)
# Convert to state-space representation
A, B, C, D = signal.tf2ss(num, den)
print("Matrix A:")
print(A)
print("Matrix B:")
print(B)
print("Matrix C:")
print(C)
print("Matrix D:")
print(D)
# Check system stability (Eigenvalues)
eigvals, eigvecs = np.linalg.eig(A)
print("Eigenvalues of A:")
print(eigvals)
stability = np.all(np.real(eigvals) < 0)
print(f"The system is {'stable' if stability else 'unstable'}.")
# Characteristic polynomial and pole placement (vector gain F)
desired_poles = np.array([-1, -2]) # Example desired poles
F = signal.place_poles(A, B, desired_poles).gain_matrix
print("Vector Gain F:")
print(F)
# Optimal regulator (LQR)
Q = np.eye(A.shape[0])
R = np.eye(B.shape[1])
P = scipy.linalg.solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R).dot(B.T).dot(P)
print("Optimal gain K (LQR):")
print(K)
# Minimum value of the evaluation function
min_eval_func_value = np.trace(P.dot(Q))
print("Minimum value of the evaluation function:")
print(min_eval_func_value)
# Eigenvalues of the Hamiltonian matrix
H = np.block([[A, -B.dot(np.linalg.inv(R)).dot(B.T)], [-Q, -A.T]])
hamilton_eigvals = np.linalg.eigvals(H)
print("Eigenvalues of the Hamiltonian matrix:")
print(hamilton_eigvals)
# Stability of the closed-loop system using the Lyapunov equation
A_cl = A - B.dot(K)
P_cl = scipy.linalg.solve_continuous_lyapunov(A_cl, -Q)
print("Solution to the Lyapunov equation for the closed-loop system P_cl:")
print(P_cl)
# Time settings for simulation
t = np.linspace(0, 10, 1000)
# Initial state
x0 = [1, 0] # Example initial state [1, 0]
# Zero-input response
_, y_zero_input, x_zero_input = signal.lsim((A_cl, B, C, D), U=0, T=t, X0=x0)
# Zero-state response
u = np.ones_like(t)
_, y_zero_state, x_zero_state = signal.lsim((A_cl, B, C, D), U=u, T=t, X0=0)
# Plotting
plt.figure(figsize=(14, 8))
# Plot zero-input response
plt.subplot(2, 1, 1)
plt.plot(t, y_zero_input, label='Zero-input Response')
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Zero-input Response')
plt.legend()
# Plot zero-state response
plt.subplot(2, 1, 2)
plt.plot(t, y_zero_state, label='Zero-state Response')
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Zero-state Response')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import scipy.linalg
import scipy.signal as signal
import matplotlib.pyplot as plt
# System parameters
A = np.array([[0, 1], [-2, -3]]) # State matrix
B = np.array([[0], [1]]) # Input matrix
C = np.array([[1, 0]]) # Output matrix
D = np.array([[0]]) # Feedforward matrix
# Noise parameters
Q = np.array([[1, 0], [0, 1]]) # Process noise covariance
R = np.array([[1]]) # Measurement noise covariance
# Calculate steady-state Kalman gain using the discrete-time algebraic Riccati equation
P = scipy.linalg.solve_continuous_are(A, C.T, Q, R)
K = P @ C.T @ np.linalg.inv(R)
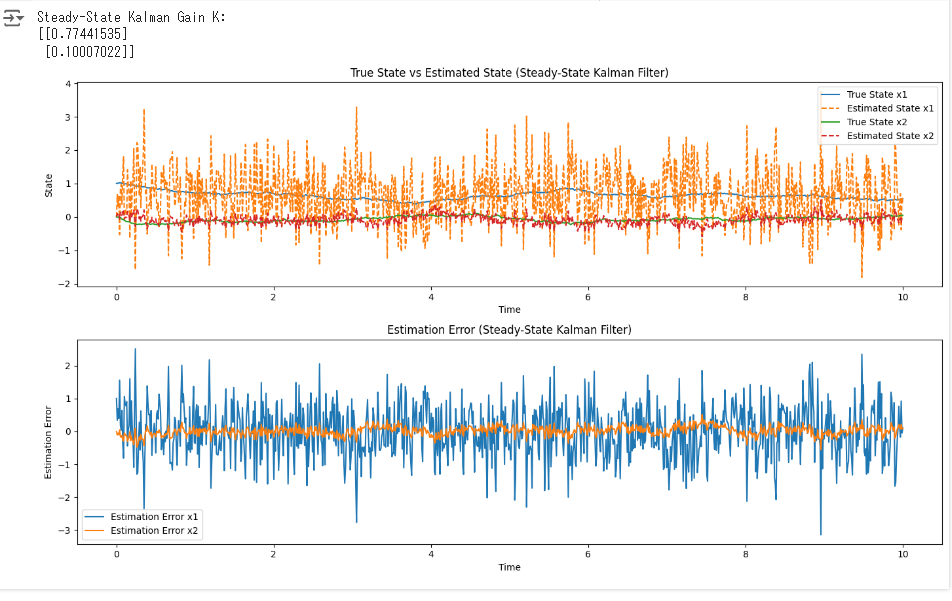
print("Steady-State Kalman Gain K:")
print(K)
# Time settings for simulation
t = np.linspace(0, 10, 1000)
dt = t[1] - t[0]
# System noise and measurement noise
np.random.seed(42) # For reproducibility
process_noise = np.random.normal(0, np.sqrt(Q[0, 0]), size=(len(t), 2))
measurement_noise = np.random.normal(0, np.sqrt(R[0, 0]), len(t))
# Initial states
x = np.zeros((len(t), 2)) # True state
x_hat = np.zeros((len(t), 2)) # Estimated state
x[0] = [1, 0] # Initial true state
x_hat[0] = [0, 0] # Initial estimated state
# Input signal
u = np.ones_like(t) # Example input
# State estimation with steady-state Kalman filter
for i in range(1, len(t)):
# True state update
x[i] = x[i-1] + (A @ x[i-1] + B.flatten() * u[i-1]) * dt + process_noise[i-1] * dt
# Measurement update
y = C @ x[i] + measurement_noise[i]
# Prediction
x_hat_minus = x_hat[i-1] + (A @ x_hat[i-1] + B.flatten() * u[i-1]) * dt
# Update
x_hat[i] = x_hat_minus + K.flatten() * (y - C @ x_hat_minus)
# Plotting results
plt.figure(figsize=(14, 8))
# Plot true state vs estimated state
plt.subplot(2, 1, 1)
plt.plot(t, x[:, 0], label='True State x1')
plt.plot(t, x_hat[:, 0], label='Estimated State x1', linestyle='dashed')
plt.plot(t, x[:, 1], label='True State x2')
plt.plot(t, x_hat[:, 1], label='Estimated State x2', linestyle='dashed')
plt.xlabel('Time')
plt.ylabel('State')
plt.title('True State vs Estimated State (Steady-State Kalman Filter)')
plt.legend()
# Plot estimation error
estimation_error = x - x_hat
plt.subplot(2, 1, 2)
plt.plot(t, estimation_error[:, 0], label='Estimation Error x1')
plt.plot(t, estimation_error[:, 1], label='Estimation Error x2')
plt.xlabel('Time')
plt.ylabel('Estimation Error')
plt.title('Estimation Error (Steady-State Kalman Filter)')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# カルマンフィルタの実装例
def kalman_filter(A, B, C, Q, R, x0, P0, measurements):
n = len(A)
m = len(measurements)
# 初期化
x = x0
P = P0
filtered_states = []
for measurement in measurements:
# 予測ステップ
x = A @ x
P = A @ P @ A.T + Q
# 更新ステップ
K = P @ C.T @ np.linalg.inv(C @ P @ C.T + R)
x = x + K @ (measurement - C @ x)
P = (np.eye(n) - K @ C) @ P
filtered_states.append(x)
return np.array(filtered_states)
# テスト用のシステムモデルと外乱
A = np.array([[0.8, 0.2],
[0.1, 0.9]])
B = np.eye(2)
C = np.eye(2)
Q = np.eye(2) * 0.01 # プロセスノイズ共分散行列
R = np.eye(2) * 0.1 # 観測ノイズ共分散行列
# 初期状態と共分散行列
x0 = np.array([0., 0.])
P0 = np.eye(2)
# ランダムな外乱の生成
np.random.seed(0)
t = np.arange(0, 10, 0.1)
disturbance = 0.1 * np.random.randn(len(t), 2)
# 測定
measurements = np.dot(A, x0) + disturbance
# カルマンフィルタを用いて推定
filtered_states = kalman_filter(A, B, C, Q, R, x0, P0, measurements)
# 結果のプロット
plt.figure(figsize=(12, 6))
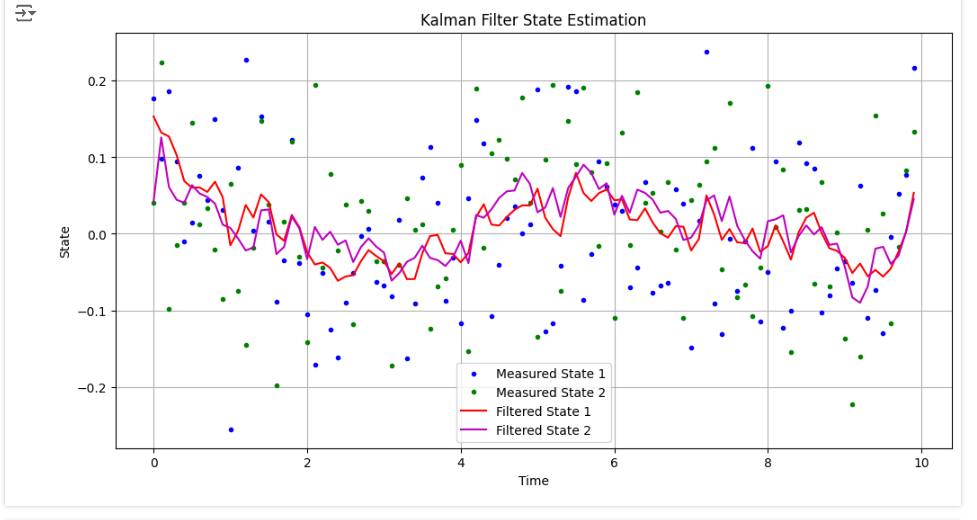
plt.plot(t, measurements[:, 0], 'b.', label='Measured State 1')
plt.plot(t, measurements[:, 1], 'g.', label='Measured State 2')
plt.plot(t, filtered_states[:, 0], 'r-', label='Filtered State 1')
plt.plot(t, filtered_states[:, 1], 'm-', label='Filtered State 2')
plt.title('Kalman Filter State Estimation')
plt.xlabel('Time')
plt.ylabel('State')
plt.legend()
plt.grid(True)
plt.show()
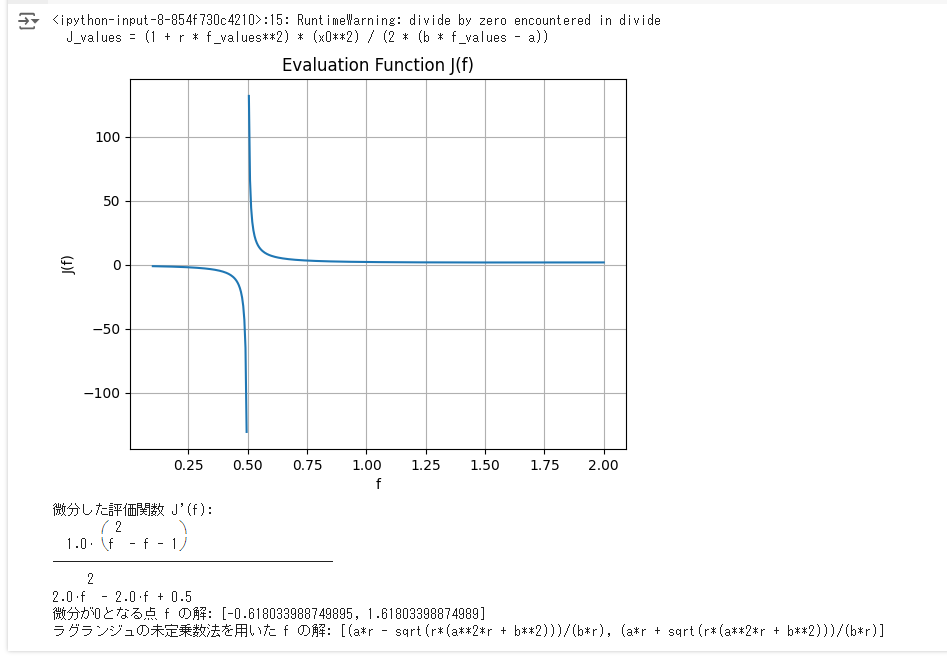
一次遅れ系伝達関数のフィードバックゲインfを求める評価関数
J(f)=(1+rf^2)((x0)^2)/(2(bf-a))
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
# パラメータの設定
r = 1.0
x0 = 1.0
a = 0.5
b = 1.0
# fの範囲設定
f_values = np.linspace(0.1, 2.0, 400) # 0.1 から 2.0 までの400点
# 評価関数 J(f) の計算
J_values = (1 + r * f_values**2) * (x0**2) / (2 * (b * f_values - a))
# 評価関数 J(f) のプロット
plt.plot(f_values, J_values)
plt.xlabel('f')
plt.ylabel('J(f)')
plt.title('Evaluation Function J(f)')
plt.grid(True)
plt.show()
# シンボリック変数の定義
f = sp.symbols('f')
J = (1 + r * f**2) * (x0**2) / (2 * (b * f - a))
# 評価関数の微分
J_diff = sp.diff(J, f)
J_diff_simplified = sp.simplify(J_diff)
# 微分した評価関数を表示
print("微分した評価関数 J'(f):")
sp.pretty_print(J_diff_simplified)
# 微分が0となる点を求める
f_solutions = sp.solve(J_diff_simplified, f)
print("微分が0となる点 f の解:", f_solutions)
# ラグランジュの未定乗数法を用いて最小値を求める
# シンボリック変数の定義
f, r, x0, a, b = sp.symbols('f r x0 a b')
# 評価関数の定義
J = (1 + r * f**2) * (x0**2) / (2 * (b * f - a))
# ラグランジュの未定乗数法を用いる
J_diff = sp.diff(J, f)
J_diff_simplified = sp.simplify(J_diff)
# 微分が0となる点を求める
f_solutions = sp.solve(J_diff_simplified, f)
print("ラグランジュの未定乗数法を用いた f の解:", f_solutions)
import numpy as np
from scipy.linalg import eig, solve_continuous_are
import matplotlib.pyplot as plt
# Define the parameters
g = 9.81 # acceleration due to gravity (m/s^2)
l = 1.0 # length of the pendulum (m)
# State-space representation
A = np.array([[0, 1], [2*g/l, 0]])
B = np.array([[0], [2/l]])
C = np.array([[1, 0]])
D = np.array([[0]])
# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = eig(A)
# Define the desired poles for the closed-loop system
desired_poles = np.array([-2, -3])
# Compute the feedback gain matrix using the pole placement method
from scipy.signal import place_poles
place_obj = place_poles(A, B, desired_poles)
K = place_obj.gain_matrix
# Closed-loop system matrix
A_cl = A - B @ K
# Diagonal canonical form (Jordan form)
eigenvalues_cl, T = eig(A_cl)
J = np.diag(eigenvalues_cl)
# Controllability matrix
ctrb = np.hstack([B, A @ B])
rank_ctrb = np.linalg.matrix_rank(ctrb)
# Plotting eigenvalues
plt.figure(figsize=(10, 6))
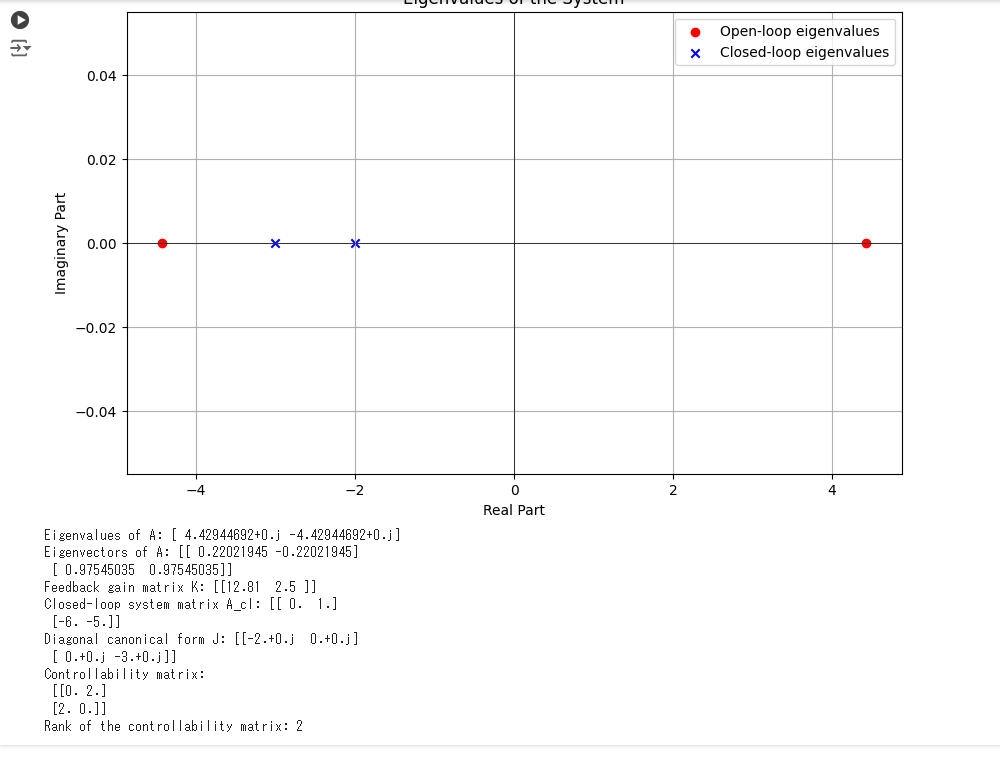
plt.scatter(eigenvalues.real, eigenvalues.imag, color='red', marker='o', label='Open-loop eigenvalues')
plt.scatter(eigenvalues_cl.real, eigenvalues_cl.imag, color='blue', marker='x', label='Closed-loop eigenvalues')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.xlabel('Real Part')
plt.ylabel('Imaginary Part')
plt.title('Eigenvalues of the System')
plt.legend()
plt.grid()
plt.show()
# Printing results
print("Eigenvalues of A:", eigenvalues)
print("Eigenvectors of A:", eigenvectors)
print("Feedback gain matrix K:", K)
print("Closed-loop system matrix A_cl:", A_cl)
print("Diagonal canonical form J:", J)
print("Controllability matrix:\n", ctrb)
print("Rank of the controllability matrix:", rank_ctrb)
import numpy as np
import scipy.signal as signal
import scipy.linalg as linalg
# 1. 伝達関数の定義
numerator = [1, 5, 3]
denominator = [1, 3, 2]
# 2. 状態空間表現への変換
system = signal.TransferFunction(numerator, denominator)
A, B, C, D = signal.tf2ss(system.num, system.den)
# 3. 制御可能標準形への変換
def controllable_form(A, B, C, D):
n = A.shape[0]
cont_matrix = np.hstack([B] + [A**i @ B for i in range(1, n)])
T = linalg.inv(cont_matrix)
A_c = T @ A @ np.linalg.inv(T)
B_c = T @ B
C_c = C @ np.linalg.inv(T)
D_c = D
return A_c, B_c, C_c, D_c
A_c, B_c, C_c, D_c = controllable_form(A, B, C, D)
# 4. 閉ループ極の設定
desired_poles = np.array([-1, -2])
# 5. 状態フィードバックゲインの計算
place = signal.place_poles(A_c, B_c, desired_poles)
K = place.gain_matrix
# 6. 閉ループシステム行列の計算
A_cl = A_c - B_c @ K
# 結果の表示
print("A_c:", A_c)
print("B_c:", B_c)
print("C_c:", C_c)
print("D_c:", D_c)
print("K:", K)
print("A_cl:", A_cl)
import numpy as np
from scipy.signal import place_poles
# 与えられたシステム行列 A, B, C, D を定義する(例として)
A = np.array([[0, 1], [-1, -1]])
B = np.array([[0], [1]])
C = np.array([[1, 0]])
D = np.array([[0]])
# オブザーバーの極を指定する
observer_poles = np.array([-10, -11])
# オブザーバーのゲイン L を求める
L = place_poles(A.T, C.T, observer_poles).gain_matrix.T
print("Observer Gain L:")
print(L)
# オブザーバーのシステム行列 A_obs を求める
A_obs = A - L @ C
print("\nObserver System Matrix A_obs:")
print(A_obs)
# オブザーバーの極を求める
observer_eigenvalues, _ = np.linalg.eig(A_obs)
print("\nObserver Eigenvalues:")
print(observer_eigenvalues)
# 可制御行列を求める
Qc = np.hstack((B, A @ B))
rank_Qc = np.linalg.matrix_rank(Qc)
print("\nControllability Matrix Qc:")
print(Qc)
print("\nRank of Qc:", rank_Qc)
# 可制御か不可制御かを判定する
if rank_Qc == A.shape[0]:
print("\nThe system is controllable.")
else:
print("\nThe system is uncontrollable.")
# 対角変換行列を求める
eigenvalues, T = np.linalg.eig(A)
T_inv = np.linalg.inv(T)
# 対角正準形に変換する
A_canonical = T_inv @ A @ T
B_canonical = T_inv @ B
C_canonical = C @ T
print("\nCanonical Form A_canonical:")
print(A_canonical)
print("\nCanonical Form B_canonical:")
print(B_canonical)
print("\nCanonical Form C_canonical:")
print(C_canonical)
import numpy as np
import matplotlib.pyplot as plt
# 対角正準形の状態方程式パラメータを設定する(例として)
A_canonical = np.array([[0, 1], [-1, -1]]) # A行列
B_canonical = np.array([[0], [1]]) # B行列
C_canonical = np.array([[1, 0]]) # C行列
D_canonical = np.array([[0]]) # D行列
# 制御対象の状態方程式を定義する
A_sys = A_canonical.copy()
B_sys = B_canonical.copy()
C_sys = C_canonical.copy()
D_sys = D_canonical.copy()
# オブザーバの設計
observer_poles = np.array([-10, -11])
L = np.transpose(place_poles(A_sys.T, C_sys.T, observer_poles).gain_matrix)
# コントローラの設計
controller_poles = np.array([-1, -2])
K = place_poles(A_sys, B_sys, controller_poles).gain_matrix
# 制御対象の極を求める
system_eigenvalues, _ = np.linalg.eig(A_sys)
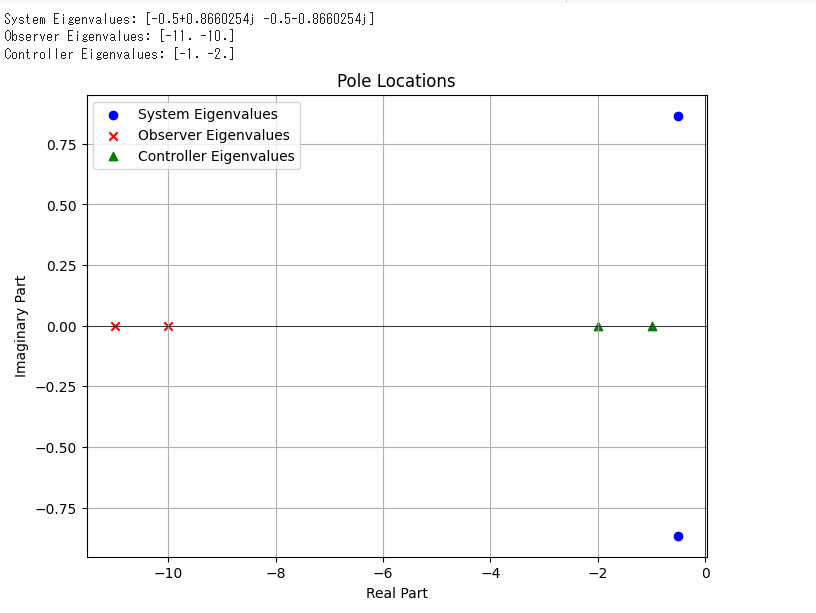
print("System Eigenvalues:", system_eigenvalues)
# オブザーバの極を求める
observer_eigenvalues, _ = np.linalg.eig(A_sys - L @ C_sys)
print("Observer Eigenvalues:", observer_eigenvalues)
# コントローラの極を求める
controller_eigenvalues, _ = np.linalg.eig(A_sys - B_sys @ K)
print("Controller Eigenvalues:", controller_eigenvalues)
# 極の位置をプロットする
plt.figure(figsize=(8, 6))
plt.scatter(system_eigenvalues.real, system_eigenvalues.imag, marker='o', color='blue', label='System Eigenvalues')
plt.scatter(observer_eigenvalues.real, observer_eigenvalues.imag, marker='x', color='red', label='Observer Eigenvalues')
plt.scatter(controller_eigenvalues.real, controller_eigenvalues.imag, marker='^', color='green', label='Controller Eigenvalues')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.xlabel('Real Part')
plt.ylabel('Imaginary Part')
plt.title('Pole Locations')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
from scipy.optimize import minimize
# 初期状態 x0、スカラー値として定義する
x0 = 1.0
# システムパラメータを定義する
a = 0.5
b = 2.0
c = 1.0
# 評価関数を定義する(この例では二乗誤差を最小化する)
def cost_function(K):
# クローズドループシステムの状態空間表現を定義する
A_cl = a - b * K
B_cl = b
C_cl = c
# 初期状態を定義する
x = np.array([x0])
# シミュレーション時間とステップサイズを定義する
T = 10 # シミュレーション時間
dt = 0.01 # ステップサイズ
time = np.arange(0, T, dt)
# クローズドループのシミュレーションを実行する
for t in time:
u = -K * x[-1] # フィードバック制御則
x_dot = A_cl * x[-1] + B_cl * u
x = np.vstack((x, x[-1] + x_dot * dt))
# 出力を計算する
y = C_cl * x[1:]
# 評価関数を計算する(この例では出力の二乗和を最小化する)
J = np.sum((y - 0)**2) # 目標出力0との差の二乗和
return J
# 初期ゲイン値を設定する
K_initial = 1.0
# 最小化アルゴリズムを使用して最小値を見つける
result = minimize(cost_function, K_initial)
# 最小値を与えるフィードバックゲインを取得する
K_optimal = result.x
print("Optimal Feedback Gain K:", K_optimal)
# プロットするための準備
# フィードバックゲインに対する評価関数の変化をプロットする場合、ここにプロットコードを追加します。
import numpy as np
from scipy.linalg import solve_continuous_are, eig
# 倒立振子モデルのパラメータを定義する
g = 9.81 # 重力加速度 [m/s^2]
l = 1.0 # 振子の長さ [m]
# システムパラメータを定義する
A = np.array([[0, 1], [-2 * g / l, 0]])
B = np.array([[0], [2 / l]])
C = np.array([[1, 0]])
D = np.array([[0]])
# 評価関数の重み行列を設定する
Q = np.eye(2) # 状態の重み行列
R = np.array([[1]]) # 入力の重み行列
# リッカチ方程式の解を計算する
P = solve_continuous_are(A, B, Q, R)
# リッカチ方程式の正定値解を確認する
eigenvalues_P, _ = eig(P)
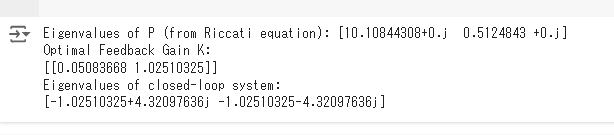
print("Eigenvalues of P (from Riccati equation):", eigenvalues_P)
# 最適フィードバックゲインを計算する
K_optimal = np.linalg.inv(R) @ B.T @ P
print("Optimal Feedback Gain K:")
print(K_optimal)
# 閉ループシステムのシステム行列を計算する
A_cl = A - B @ K_optimal
# 閉ループシステムの極を計算する
eigenvalues_cl, _ = eig(A_cl)
print("Eigenvalues of closed-loop system:")
print(eigenvalues_cl)
import numpy as np
import scipy.linalg
import matplotlib.pyplot as plt
# システムのパラメータを定義します
A = np.array([[0, 1],
[-2, -3]])
B = np.array([[0],
[1]])
Q = np.array([[1, 0],
[0, 1]])
R = np.array([[1]])
# リッカチ方程式を解きます
P = scipy.linalg.solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R) @ B.T @ P
# 行列PとKを表示
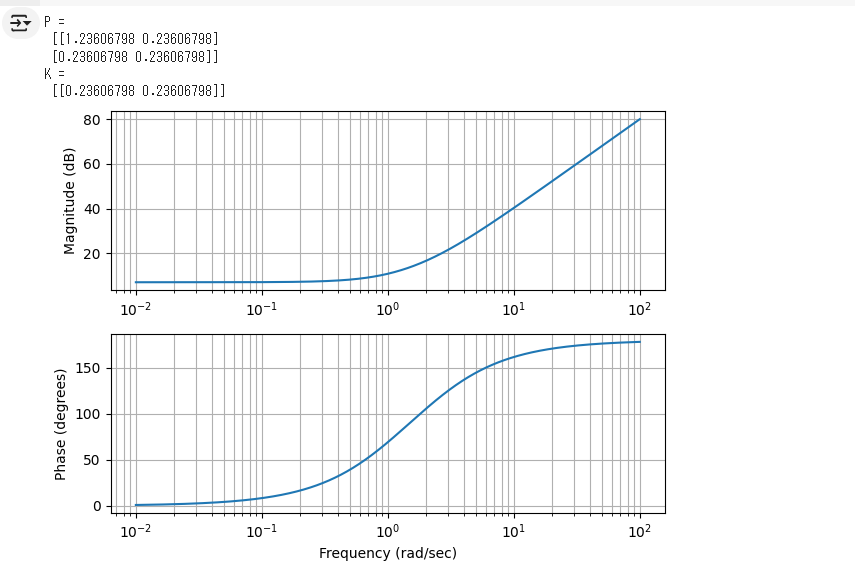
print("P =\n", P)
print("K =\n", K)
# システムの閉ループ行列を計算します
Acl = A - B @ K
# 周波数特性を計算します
frequencies = np.logspace(-2, 2, 500)
H = np.zeros_like(frequencies, dtype=complex)
for i, w in enumerate(frequencies):
H[i] = np.linalg.det(1j * w * np.eye(Acl.shape[0]) - Acl)
# 周波数特性をプロットします
magnitude = 20 * np.log10(np.abs(H))
phase = np.angle(H, deg=True)
plt.figure()
plt.subplot(211)
plt.semilogx(frequencies, magnitude)
plt.ylabel('Magnitude (dB)')
plt.grid(which='both', axis='both')
plt.subplot(212)
plt.semilogx(frequencies, phase)
plt.xlabel('Frequency (rad/sec)')
plt.ylabel('Phase (degrees)')
plt.grid(which='both', axis='both')
plt.tight_layout()
plt.show()
import numpy as np
import cvxpy as cp
# システム行列の定義(例としてランダムな行列を使用)
A = np.array([[1.0, 2.0], [-3.0, 4.0]])
B = np.array([[1.0], [0.0]])
# LMI変数の定義
P = cp.Variable((A.shape[0], A.shape[1]), symmetric=True)
Y = cp.Variable((B.shape[1], A.shape[0]))
# LMI条件の設定
constraints = [
P >> 0,
A @ P + P @ A.T + B @ Y + Y.T @ B.T << 0
]
# 目的関数(適当に設定)
objective = cp.Minimize(cp.trace(P))
# 最適化問題の定義
prob = cp.Problem(objective, constraints)
# 解を求める
prob.solve()
# 結果の表示
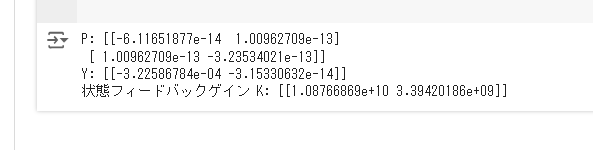
print("P:", P.value)
print("Y:", Y.value)
# 状態フィードバックゲインの計算
K = Y.value @ np.linalg.inv(P.value)
print("状態フィードバックゲイン K:", K)
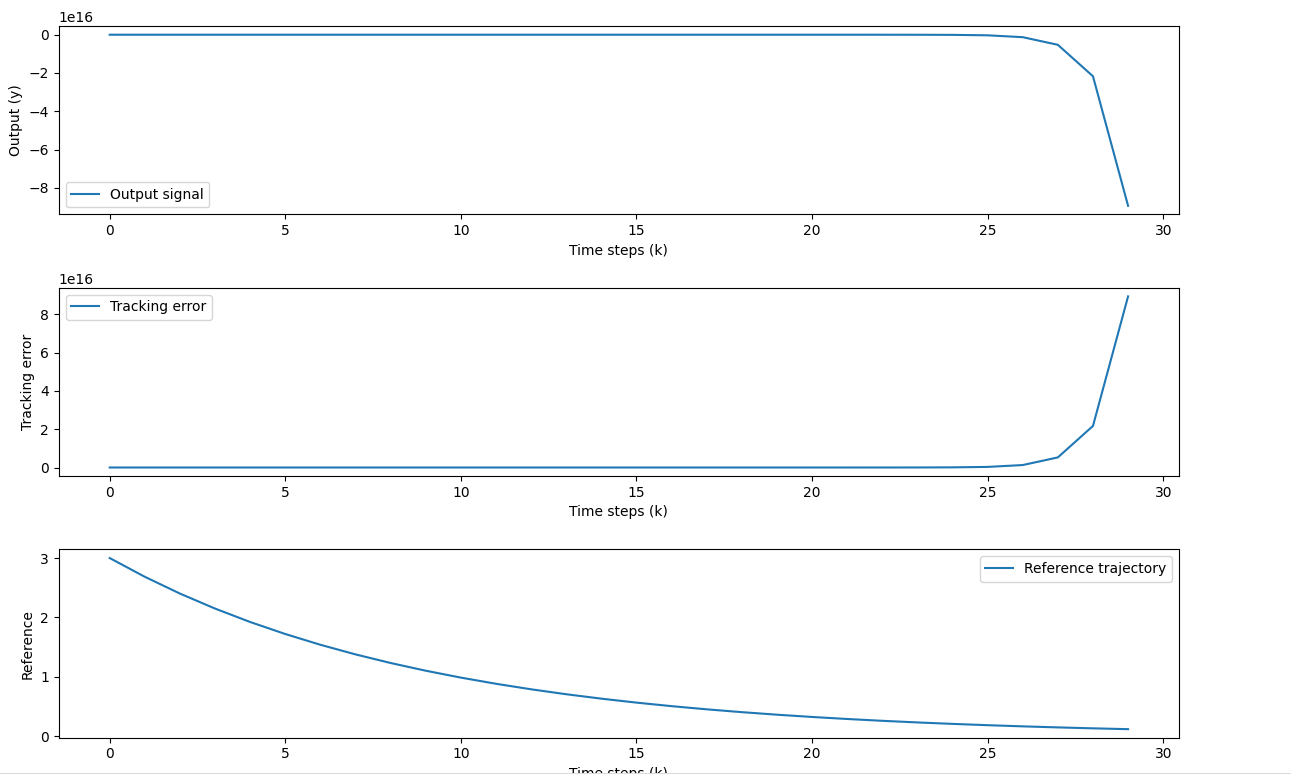
import numpy as np
import matplotlib.pyplot as plt
# Discrete transfer function parameters
b = [2] # Numerator coefficients
a = [1, -0.7] # Denominator coefficients
# Sampling period
T = 3 # seconds
# Time vector
k = np.arange(0, 30) # Assuming 30 time steps
# Reference trajectory: exponential decay with time constant Tref = 9s
Tref = 9
reference = 3 * np.exp(-k / Tref)
# Output signal computation
y = np.zeros_like(k, dtype=float)
u = np.zeros_like(k, dtype=float)
# Initial conditions
y[0] = 2
u[0] = 0.3
for i in range(1, len(k)):
# Calculate control input u using predictive control law
if i > 1:
u[i-1] = b[0] * y[i-1] - a[1] * u[i-2]
# Simulate the system response
y[i] = b[0] * u[i-1] + a[1] * y[i-1]
# Plotting
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(k, y, label='Output signal')
plt.xlabel('Time steps (k)')
plt.ylabel('Output (y)')
plt.legend()
plt.subplot(3, 1, 2)
tracking_error = reference - y[:len(reference)]
plt.plot(k[:len(reference)], tracking_error, label='Tracking error')
plt.xlabel('Time steps (k)')
plt.ylabel('Tracking error')
plt.legend()
plt.subplot(3, 1, 3)
plt.plot(k[:len(reference)], reference, label='Reference trajectory')
plt.xlabel('Time steps (k)')
plt.ylabel('Reference')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.optimize import least_squares
# システムダイナミクスをシミュレートする関数
def simulate_system(A, B, x0, u, noise_std=0.1):
n = len(x0)
T = len(u[0])
x = np.zeros((n, T+1))
x[:, 0] = x0
for t in range(T):
x[:, t+1] = A @ x[:, t] + B @ u[:, t] + np.random.normal(0, noise_std, size=(n,))
return x[:, :-1], x[:, 1:]
# 最小二乗法を使用して状態空間行列 A と入力行列 B を推定する関数
def estimate_state_space(A_guess, B_guess, y, u):
n = A_guess.shape[0]
m = B_guess.shape[1]
T = y.shape[1]
def residual(params):
A_est = params[:n*n].reshape((n, n))
B_est = params[n*n:].reshape((n, m))
# 擬似逆行列を使用して初期状態 x0_est を推定
x0_est = np.linalg.solve(np.eye(n) - A_est, B_est @ u[:, 0])
# 推定されたパラメータでシステムをシミュレート
x_sim, _ = simulate_system(A_est, B_est, x0_est, u)
return (y - x_sim).flatten()
# パラメータの初期推定値
init_params = np.concatenate((A_guess.flatten(), B_guess.flatten()))
# 最小二乗法による最適化
result = least_squares(residual, init_params)
# 推定されたシステム行列
A_est = result.x[:n*n].reshape((n, n))
B_est = result.x[n*n:].reshape((n, m))
return A_est, B_est
# 使用例
n = 2 # 状態の数
m = 1 # 入力の数
T = 100 # サンプル数
A_true = np.array([[0.9, 0.1], [0, 0.8]]) # 真のシステム行列
B_true = np.array([[1], [0.5]]) # 真の入力行列
x0_true = np.array([1, 0.5]) # 初期状態ベクトル
u = np.random.randn(m, T) # ランダムな入力ベクトル
# システムダイナミクスをシミュレートしてサンプルデータを生成
x_true, _ = simulate_system(A_true, B_true, x0_true, u)
# 観測データにノイズを加える
noise_std = 0.1
y = x_true + np.random.normal(0, noise_std, size=x_true.shape)
# システム行列の初期推定値
A_guess = np.random.randn(n, n)
B_guess = np.random.randn(n, m)
# 最小二乗法を使用してシステム行列を推定
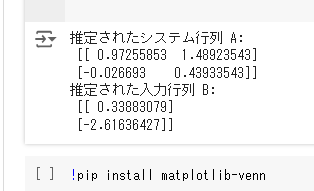
A_est, B_est = estimate_state_space(A_guess, B_guess, y, u)
print("推定されたシステム行列 A:\n", A_est)
print("推定された入力行列 B:\n", B_est)
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_discrete_are
# System parameters
A = np.array([[1.1, 2], [0, 0.95]])
B = np.array([[0], [0.0787]])
C = np.array([[1, 0]])
Q = np.eye(2)
R = np.eye(1)
# Solve the discrete-time Riccati equation
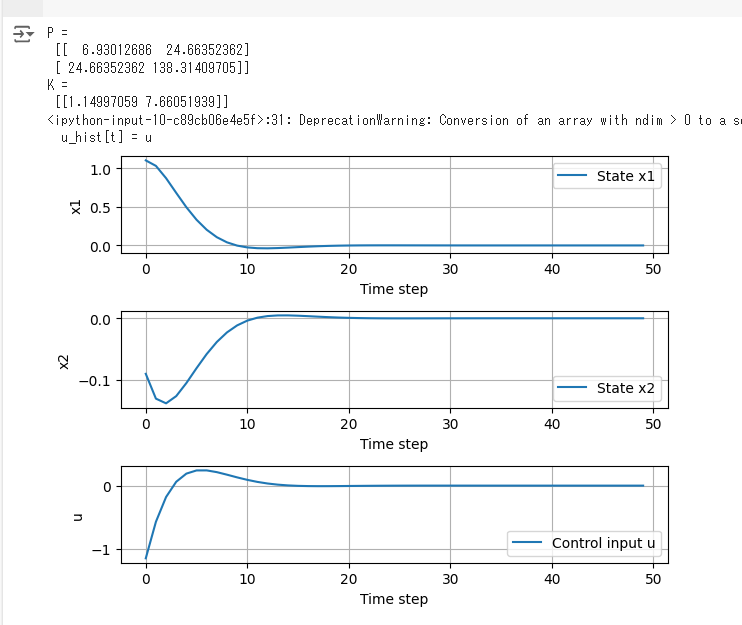
P = solve_discrete_are(A, B, Q, R)
K = np.linalg.inv(B.T @ P @ B + R) @ (B.T @ P @ A)
# Print the matrices P and K
print("P =\n", P)
print("K =\n", K)
# Simulation parameters
x = np.array([[1], [0]]) # Initial state
n_steps = 50
x_hist = np.zeros((2, n_steps))
u_hist = np.zeros(n_steps)
# Simulation loop
for t in range(n_steps):
u = -K @ x
x = A @ x + B @ u
x_hist[:, t] = x.ravel()
u_hist[t] = u
# Plot the results
plt.figure()
plt.subplot(311)
plt.plot(x_hist[0, :], label='State x1')
plt.xlabel('Time step')
plt.ylabel('x1')
plt.grid()
plt.legend()
plt.subplot(312)
plt.plot(x_hist[1, :], label='State x2')
plt.xlabel('Time step')
plt.ylabel('x2')
plt.grid()
plt.legend()
plt.subplot(313)
plt.plot(u_hist, label='Control input u')
plt.xlabel('Time step')
plt.ylabel('u')
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
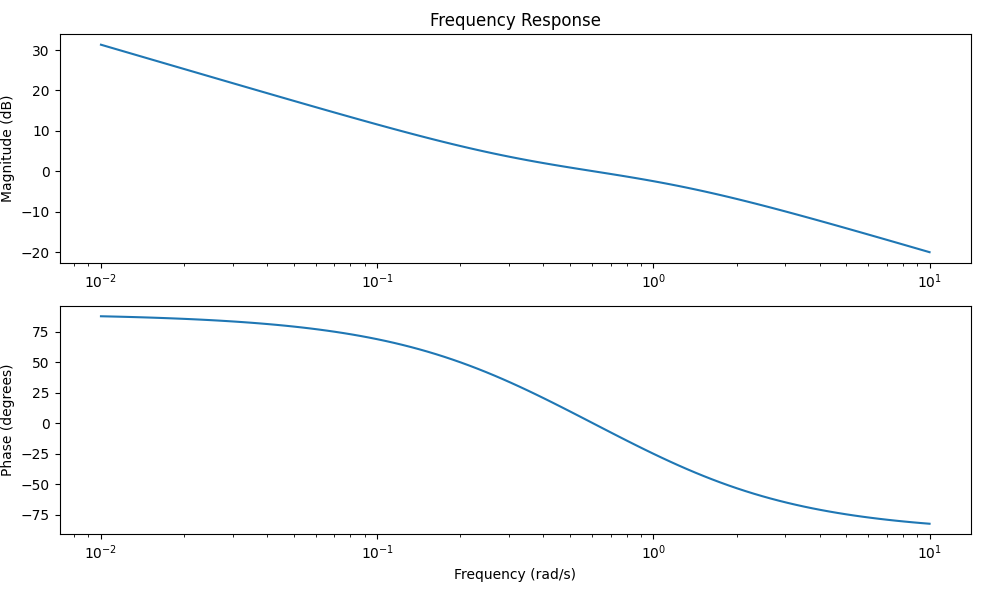
# Define the Zero-Order Hold (ZOH) as a transfer function in the continuous domain
# ZOH in continuous domain can be approximated as (1 - e^(-sT))/s
T = 1 # Sampling period, example value
zoh_num = [1, -np.exp(-T)]
zoh_den = [T, 0]
zoh_tf = signal.TransferFunction(zoh_num, zoh_den)
# Define the control target transfer function (1/(1 + as))
a = 1 # Example value for a
control_target_tf = signal.TransferFunction([1], [1, a])
# Multiply the transfer functions
# (ZOH * control target) in continuous domain
combined_num = np.polymul(zoh_tf.num, control_target_tf.num)
combined_den = np.polymul(zoh_tf.den, control_target_tf.den)
combined_tf = signal.TransferFunction(combined_num, combined_den)
# Frequency response of the combined system
w, mag, phase = signal.bode(combined_tf)
# Plot the magnitude and phase response
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.semilogx(w, mag) # Bode magnitude plot
plt.title('Frequency Response')
plt.ylabel('Magnitude (dB)')
plt.subplot(2, 1, 2)
plt.semilogx(w, phase) # Bode phase plot
plt.ylabel('Phase (degrees)')
plt.xlabel('Frequency (rad/s)')
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Generate synthetic data
np.random.seed(0)
N = 100 # Number of samples
t = np.linspace(0, 10, N)
u = np.sin(t) # Input signal
a_true = 2.0 # True value of a
b_true = 1.0 # True value of b
noise = 0.5 * np.random.randn(N) # Gaussian noise
y = a_true * u + b_true + noise # Output signal
# Least Squares Method for system identification
A = np.vstack([u, np.ones(len(u))]).T
a_est, b_est = np.linalg.lstsq(A, y, rcond=None)[0]
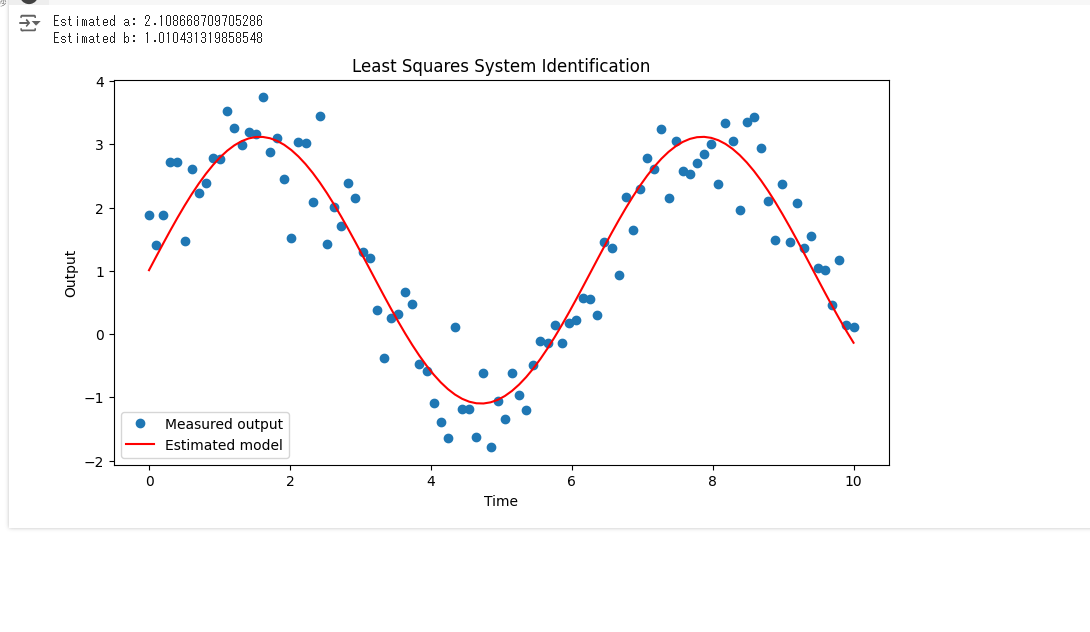
print(f"Estimated a: {a_est}")
print(f"Estimated b: {b_est}")
# Plot results
plt.figure(figsize=(10, 5))
plt.plot(t, y, 'o', label='Measured output')
plt.plot(t, a_est * u + b_est, 'r', label='Estimated model')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Least Squares System Identification')
plt.show()
from scipy.optimize import minimize
# Prediction error method for system identification
def prediction_error(params, u, y):
a, b = params
y_pred = a * u + b
error = y - y_pred
return np.sum(error**2)
# Initial guess for parameters
initial_guess = [1.0, 0.0]
# Perform optimization to minimize the prediction error
result = minimize(prediction_error, initial_guess, args=(u, y))
a_est, b_est = result.x
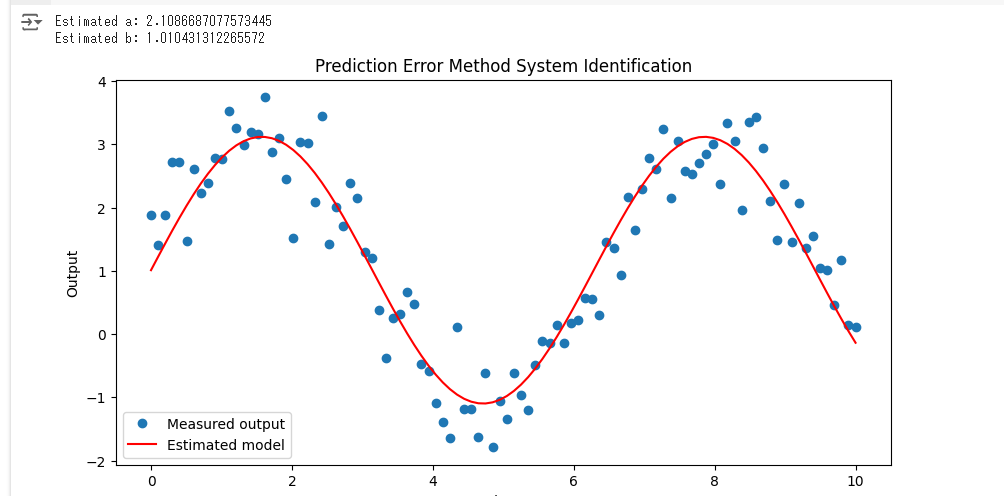
print(f"Estimated a: {a_est}")
print(f"Estimated b: {b_est}")
# Plot results
plt.figure(figsize=(10, 5))
plt.plot(t, y, 'o', label='Measured output')
plt.plot(t, a_est * u + b_est, 'r', label='Estimated model')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Output')
plt.title('Prediction Error Method System Identification')
plt.show()
from scipy.linalg import solve_continuous_are
# System matrices
A = np.array([[0, 1], [-2, -3]])
B = np.array([[0], [1]])
Q = np.eye(2) # State cost matrix
R = np.eye(1) # Input cost matrix
# Solve Riccati equation
P = solve_continuous_are(A, B, Q, R)
# Optimal gain
K_opt = np.linalg.inv(R).dot(B.T).dot(P)
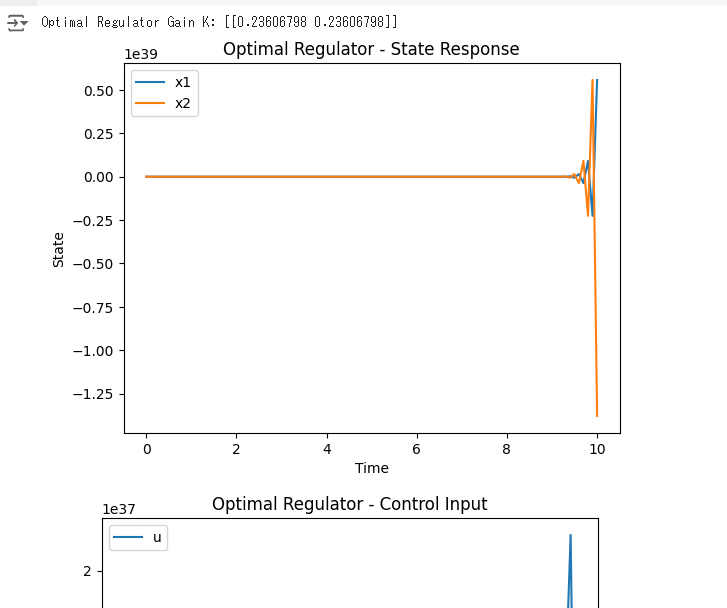
print("Optimal Regulator Gain K:", K_opt)
# Evaluation function
def cost_function(x, u):
return x.T.dot(Q).dot(x) + u.T.dot(R).dot(u)
# Plot the state response with the optimal regulator
t = np.linspace(0, 10, 100)
x0 = np.array([1, 0])
x = [x0]
u = []
for _ in t[1:]:
u_k = -K_opt.dot(x[-1])
x_k = np.dot(A - np.dot(B, K_opt), x[-1]) + np.dot(B, u_k)
x.append(x_k)
u.append(u_k)
x = np.array(x)
u = np.array(u)
plt.figure()
plt.plot(t, x)
plt.title('Optimal Regulator - State Response')
plt.xlabel('Time')
plt.ylabel('State')
plt.legend(['x1', 'x2'])
plt.show()
plt.figure()
plt.plot(t[:-1], u)
plt.title('Optimal Regulator - Control Input')
plt.xlabel('Time')
plt.ylabel('Control Input')
plt.legend(['u'])
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# Prepare the data
time_data = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) # Time data
output_data = np.array([0, 0.1, 0.3, 0.55, 0.75, 0.9, 0.95, 0.98, 0.99, 1.0, 1.0]) # Output data
# Define the first-order system step response function
def first_order_response(t, K, tau):
return K * (1 - np.exp(-t / tau))
# Initial guess for the parameters
initial_guess = [1.0, 1.0]
# Fit the model to the data using least squares
params, covariance = curve_fit(first_order_response, time_data, output_data, p0=initial_guess)
K_est, tau_est = params
# Display the results
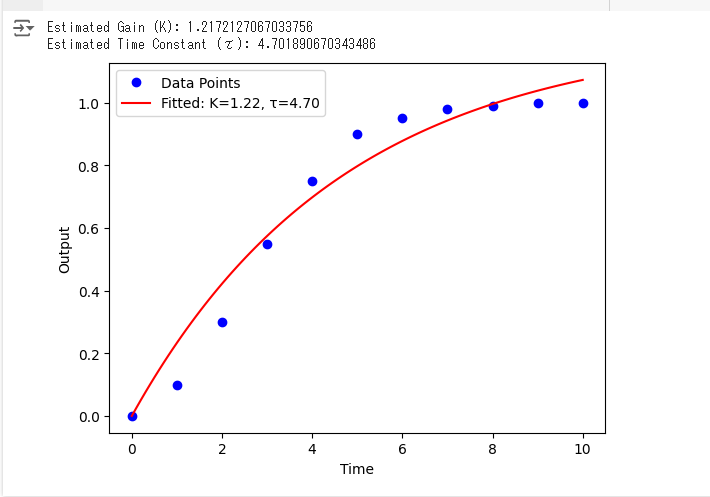
print(f"Estimated Gain (K): {K_est}")
print(f"Estimated Time Constant (τ): {tau_est}")
# Plot the fitting results
plt.plot(time_data, output_data, 'bo', label='Data Points')
time_fit = np.linspace(0, max(time_data), 100)
output_fit = first_order_response(time_fit, K_est, tau_est)
plt.plot(time_fit, output_fit, 'r-', label=f'Fitted: K={K_est:.2f}, τ={tau_est:.2f}')
plt.xlabel('Time')
plt.ylabel('Output')
plt.legend()
plt.show()
import numpy as np
# サンプルデータ
t = np.array([0, 1, 2, 3, 4])
y = np.array([2.1, 4.3, 7.2, 9.9, 12.5])
# 行列形式に変換
Phi = np.vstack([np.ones_like(t), t]).T
# 重み行列(対角行列を仮定)
W = np.eye(len(t)) # ここでは単位行列を使用
# 最小二乗法による推定
theta_hat = np.linalg.inv(Phi.T @ W @ Phi) @ Phi.T @ W @ y
# 推定されたパラメータ
intercept = theta_hat[0]
slope = theta_hat[1]
# 評価関数(二乗誤差)
J = np.sum((y - Phi @ theta_hat)**2)
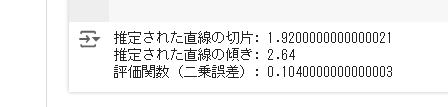
print(f"推定された直線の切片: {intercept}")
print(f"推定された直線の傾き: {slope}")
print(f"評価関数(二乗誤差): {J}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import least_squares
from scipy import signal
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# 1. システム同定
# 真のパラメータ
true_params = [2.0, 5.0] # K, tau
K_true, tau_true = true_params
# 時間軸
t = np.linspace(0, 20, 500)
# ステップ入力
u = np.ones_like(t)
# 一次遅れ系の伝達関数
system = signal.TransferFunction([K_true], [tau_true, 1])
t, y_true = signal.step(system, T=t)
# ノイズを加える
noise = 0.2 * np.random.normal(size=y_true.size)
y_noisy = y_true + noise
# 2. 最小二乗法によるパラメータ推定
def model(params, t, u):
K, tau = params
system = signal.TransferFunction([K], [tau, 1])
_, y = signal.step(system, T=t)
return y
def cost_function(params, t, u, y_noisy):
y_model = model(params, t, u)
return y_noisy - y_model
initial_guess = [1.0, 1.0]
result = least_squares(cost_function, initial_guess, args=(t, u, y_noisy))
estimated_params = result.x
# 推定されたパラメータ
K_est, tau_est = estimated_params
# 推定されたモデル
y_est = model(estimated_params, t, u)
# プロット
plt.figure(figsize=(12, 6))
# システム同定のプロット
plt.subplot(1, 2, 1)
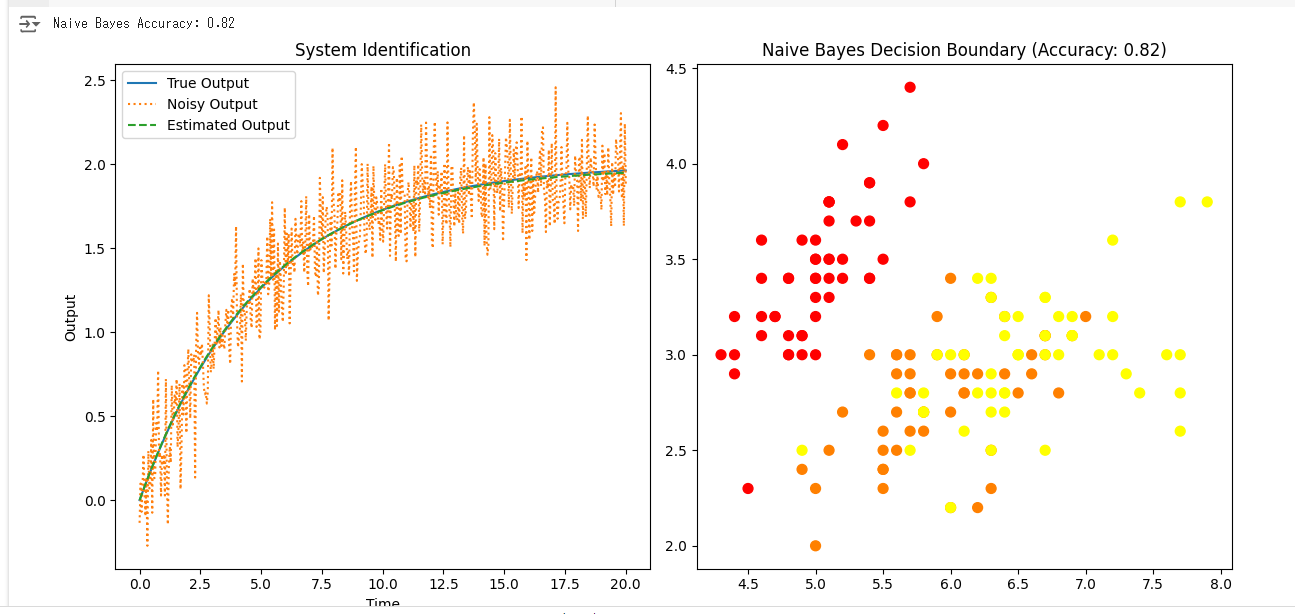
plt.plot(t, y_true, label='True Output')
plt.plot(t, y_noisy, label='Noisy Output', linestyle='dotted')
plt.plot(t, y_est, label='Estimated Output', linestyle='dashed')
plt.xlabel('Time')
plt.ylabel('Output')
plt.legend()
plt.title('System Identification')
# 3. ナイーブベイズ分類器による分類
iris = load_iris()
X = iris.data[:, :2] # 特徴量として2つの変数を使用
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
gnb = GaussianNB()
gnb.fit(X_train, y_train)
y_pred_nb = gnb.predict(X_test)
# 精度の計算
accuracy_nb = accuracy_score(y_test, y_pred_nb)
print(f'Naive Bayes Accuracy: {accuracy_nb:.2f}')
# ナイーブベイズのプロット
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.title(f'Naive Bayes Decision Boundary (Accuracy: {accuracy_nb:.2f})')
# グラフのレイアウト調整
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# 伝達関数の定義
numerator = [1]
denominator = [1, 1, 1]
sys = (numerator, denominator)
# ボード線図をプロットする関数
def bode_plot(sys):
magnitude = []
phase = []
omega = np.logspace(-2, 2, 1000) # ボード線図の周波数範囲を指定
for freq in omega:
s = 1j * freq
G = np.polyval(sys[0], s) / np.polyval(sys[1], s)
magnitude.append(20 * np.log10(abs(G)))
phase.append(np.angle(G, deg=True))
plt.figure()
plt.subplot(2, 1, 1)
plt.semilogx(omega, magnitude)
plt.title('Bode Plot - Magnitude')
plt.grid()
plt.subplot(2, 1, 2)
plt.semilogx(omega, phase)
plt.title('Bode Plot - Phase')
plt.xlabel('Frequency [rad/s]')
plt.grid()
# ロバスト安定性マージンを計算する関数
def stability_margins(sys):
K = np.polyval(sys[0], 0) / np.polyval(sys[1], 0)
L = np.polyder(sys[1])
M = np.polyval(L, 0)
gain_margin = 1 / abs(K)
phase_margin = np.degrees(np.arctan2(M, 1 - K))
return gain_margin, phase_margin
# 相補感度関数を計算してプロットする関数
def complementary_sensitivity(sys):
S_num = sys[1]
S_den = np.polyadd(sys[0], sys[1])
sys_S = (S_num, S_den)
bode_plot(sys_S)
# メインの実行部分
if __name__ == '__main__':
# ボード線図をプロット
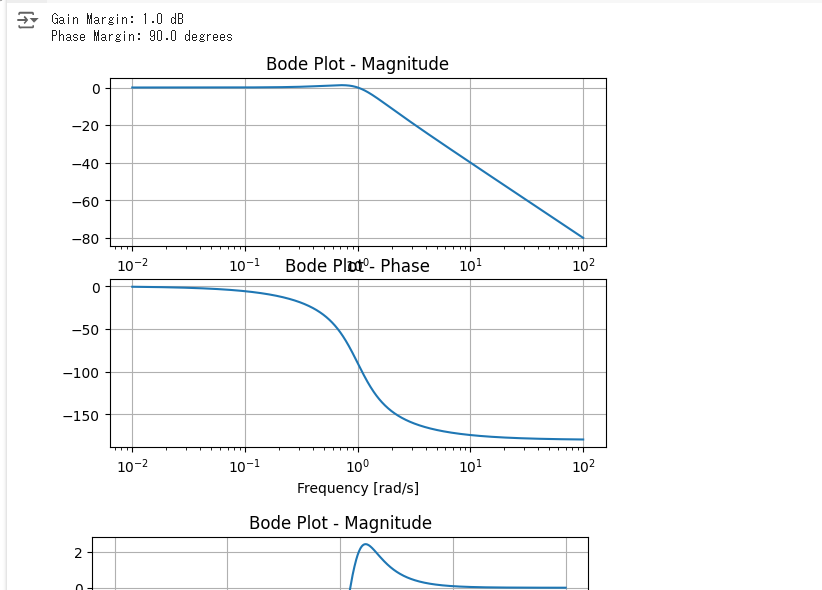
bode_plot(sys)
# ロバスト安定性マージンを計算
gm, pm = stability_margins(sys)
print(f"Gain Margin: {gm} dB")
print(f"Phase Margin: {pm} degrees")
# 相補感度関数を計算してプロット
complementary_sensitivity(sys)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# System transfer function: num/den = 1 / (s^2 + 2s + 1)
num = [1]
den = [1, 2, 1]
# Frequency weight function: W = 1 / (s + 0.5)
W_num = [1]
W_den = [1, 0.5]
# Define the Laplace variable 's'
s = 1j * np.logspace(-1, 1, 1000)
# System transfer function in Laplace domain
G = np.polyval(num, s) / np.polyval(den, s)
# Frequency weight function in Laplace domain
W = np.polyval(W_num, s) / np.polyval(W_den, s)
# Calculate closed-loop transfer function T = KG / (1 + KG)
K = 1 / W # H-infinity optimal controller K
T = K * G / (1 + K * G)
# Calculate magnitude and phase of T
mag_T = 20 * np.log10(np.abs(T))
phase_T = np.angle(T, deg=True)
# Plot Bode magnitude and phase of T
plt.figure()
plt.subplot(2, 1, 1)
plt.semilogx(np.abs(s), mag_T)
plt.grid(True)
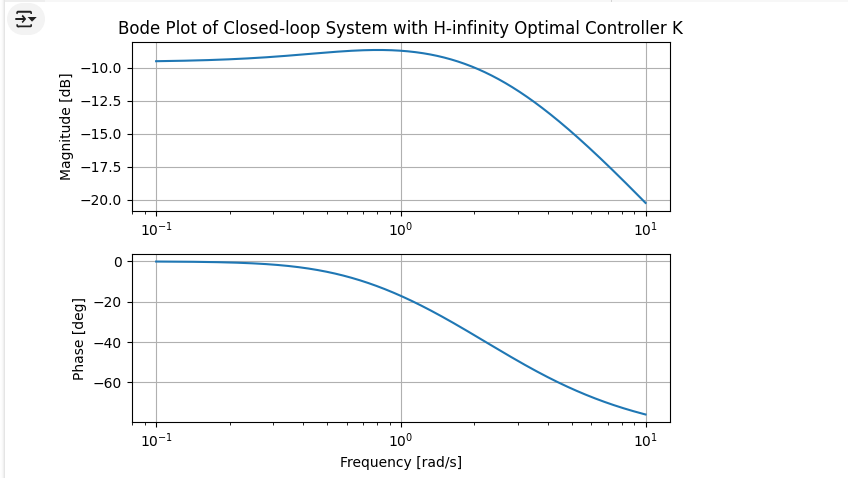
plt.ylabel('Magnitude [dB]')
plt.title('Bode Plot of Closed-loop System with H-infinity Optimal Controller K')
plt.subplot(2, 1, 2)
plt.semilogx(np.abs(s), phase_T)
plt.grid(True)
plt.ylabel('Phase [deg]')
plt.xlabel('Frequency [rad/s]')
plt.tight_layout()
plt.show()
import numpy as np
from sklearn.linear_model import Lasso
# ダミーデータの生成
np.random.seed(0)
N = 100 # データ数
T = 1.0 # サンプリング周期
tau_true = 10.0 # 真の時定数
K_true = 2.0 # 真のゲイン
x_true = np.zeros(N)
u = np.random.randn(N) # ランダムな入力データ
# 状態方程式のシミュレーション(出力データの生成)
for k in range(N-1):
x_true[k+1] = (1 - T / tau_true) * x_true[k] + (K_true * T / tau_true) * u[k]
y_true = x_true.copy() # 出力データは状態ベクトルと同じ
# ノイズの追加
noise_std = 0.1
y = y_true + np.random.randn(N) * noise_std # ノイズを加えた出力データ
# スパースモデリングによるパラメータ推定
model = Lasso(alpha=0.1) # Lasso回帰モデルを使用
X = np.column_stack([x_true[:-1], u[:-1]]) # 説明変数の設定
model.fit(X, x_true[1:]) # 状態遷移 x(k+1) の推定
# 推定されたパラメータの表示
tau_estimated = T / model.coef_[0]
K_estimated = model.coef_[1] * tau_estimated / T
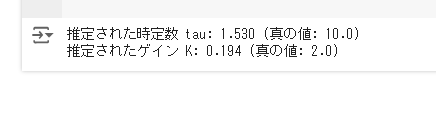
print(f"推定された時定数 tau: {tau_estimated:.3f} (真の値: {tau_true})")
print(f"推定されたゲイン K: {K_estimated:.3f} (真の値: {K_true})")
import numpy as np
from sklearn.linear_model import Lasso
import matplotlib.pyplot as plt
# サンプルデータの生成
omega_n_true = 2.0 # 真の自然角周波数
zeta_true = 0.5 # 真の減衰係数
num_points = 100
# 周波数軸の設定
freq = np.logspace(-1, 2, num_points)
omega = 2 * np.pi * freq
# 二次遅れシステムの周波数応答(真の)
H_true = omega_n_true**2 / (omega**2 + 2 * zeta_true * omega_n_true * 1j * omega + omega_n_true**2)
# ノイズを加えた測定データの生成
np.random.seed(0)
noise_level = 0.1
noise = noise_level * (np.random.randn(num_points) + 1j * np.random.randn(num_points))
H_measured = H_true + noise
# データの準備
X = np.vstack((np.real(H_measured), np.imag(H_measured))).T
y = np.abs(H_measured)
# Lasso回帰で係数の同定
lasso = Lasso(alpha=0.1) # alphaは正則化パラメータ
lasso.fit(X, y)
# 同定された係数
omega_n_identified = np.sqrt(lasso.coef_[0])
zeta_identified = lasso.coef_[1] / (2 * omega_n_identified)
# プロット
plt.figure()
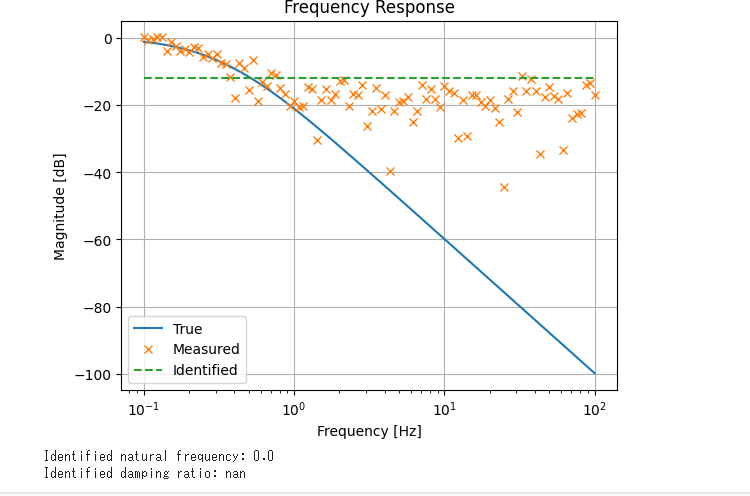
plt.semilogx(freq, 20 * np.log10(np.abs(H_true)), label='True')
plt.semilogx(freq, 20 * np.log10(np.abs(H_measured)), 'x', label='Measured')
plt.semilogx(freq, 20 * np.log10(np.abs(lasso.predict(X))), '--', label='Identified')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude [dB]')
plt.legend()
plt.grid(True)
plt.title('Frequency Response')
plt.show()
print(f"Identified natural frequency: {omega_n_identified}")
print(f"Identified damping ratio: {zeta_identified}")
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの準備
T = 10 # シミュレーション時間
dt = 0.01 # サンプリング時間
n = int(T / dt) # サンプル数
# 状態方程式のパラメータ
a = -0.5 # 状態方程式の係数
b = 1.0 # 入力の係数
c = 1.0 # 出力の係数
# 入力信号 (例として単位ステップ関数)
u = np.ones(n)
# サンプルデータから出力を生成
x_true = np.zeros(n)
y_true = np.zeros(n)
for i in range(1, n):
x_true[i] = x_true[i-1] + dt * (a * x_true[i-1] + b * u[i-1])
y_true[i] = c * x_true[i]
# ノイズの追加
noise_std = 0.1 # ノイズの標準偏差
noise = np.random.normal(0, noise_std, n)
y_noisy = y_true + noise
# 状態推定のための最小二乗法
A = np.array([[-a]])
B = np.array([[b]])
C = np.array([[c]])
X_est = np.zeros((1, n)) # 状態推定値の初期化
for i in range(1, n):
X_est[:, i] = X_est[:, i-1] + dt * (A @ X_est[:, i-1].reshape(-1, 1) + B @ u[i-1].reshape(-1, 1)).ravel()
# 評価関数の計算
def cost_function(X_est, Y):
cost = np.sum((C @ X_est - Y) ** 2)
return cost
# 正規方程式の解の計算
Y = y_noisy.reshape(1, -1) # 出力の観測値
# 評価関数の値の表示
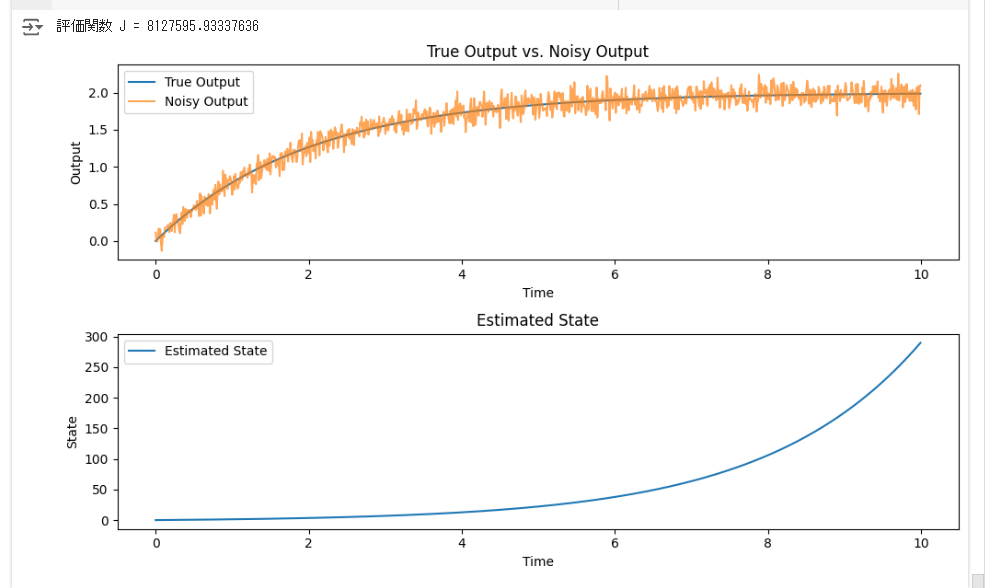
J = cost_function(X_est, Y)
print("評価関数 J =", J)
# 結果のプロット
t = np.arange(0, T, dt)
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, y_true, label='True Output')
plt.plot(t, y_noisy, label='Noisy Output', alpha=0.7)
plt.title('True Output vs. Noisy Output')
plt.xlabel('Time')
plt.ylabel('Output')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, X_est.ravel(), label='Estimated State')
plt.title('Estimated State')
plt.xlabel('Time')
plt.ylabel('State')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.signal import impulse, lti
# 真のパラメータ
omega_n_true = 2.0
zeta_true = 0.5
# インパルス応答を生成する関数
def generate_impulse_response(omega_n, zeta, t):
system = lti([omega_n**2], [1, 2*zeta*omega_n, omega_n**2])
t, y = impulse(system, T=t)
return y
# 時間軸
t = np.linspace(0, 10, 500)
# 真のインパルス応答
y_true = generate_impulse_response(omega_n_true, zeta_true, t)
# システム同定のためのフィッティング関数
def model(t, omega_n, zeta):
return generate_impulse_response(omega_n, zeta, t)
# ノイズを加える
y_noisy = y_true + 0.05 * np.random.normal(size=t.shape)
# パラメータ推定
popt, pcov = curve_fit(model, t, y_noisy, p0=[1.0, 0.1])
omega_n_est, zeta_est = popt
# 推定されたインパルス応答
y_est = generate_impulse_response(omega_n_est, zeta_est, t)
# 結果をプロット
plt.figure(figsize=(10, 6))
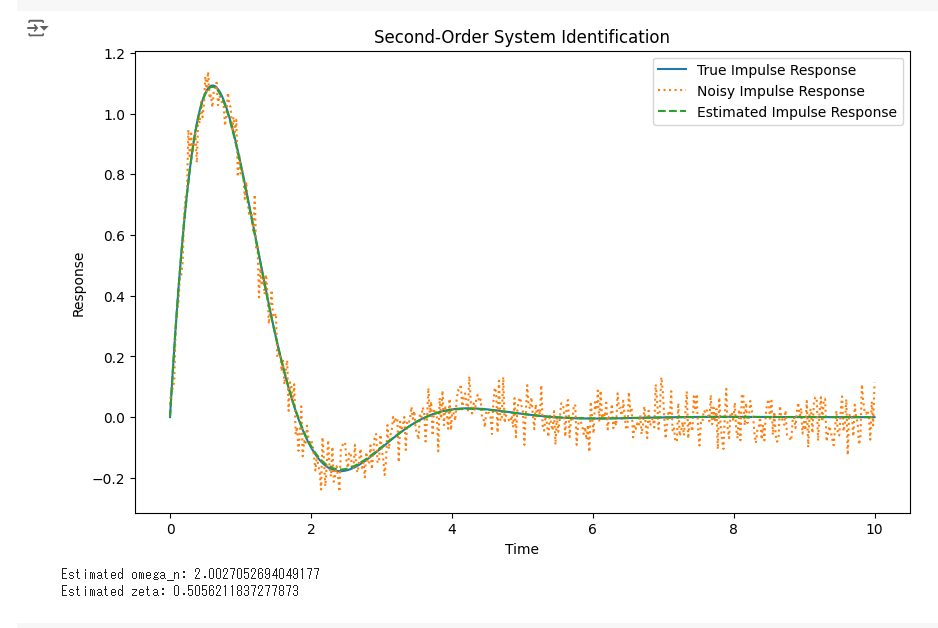
plt.plot(t, y_true, label='True Impulse Response')
plt.plot(t, y_noisy, label='Noisy Impulse Response', linestyle='dotted')
plt.plot(t, y_est, label='Estimated Impulse Response', linestyle='dashed')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Response')
plt.title('Second-Order System Identification')
plt.show()
# 推定結果を表示
print(f"Estimated omega_n: {omega_n_est}")
print(f"Estimated zeta: {zeta_est}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_discrete_are
from scipy.signal import StateSpace, dlti, dstep
# システムの状態空間モデル
A = np.array([[1.1, 2.0], [0, 1.0]])
B = np.array([[0.1], [0.2]])
C = np.array([[1.0, 0.0]])
D = np.array([[0.0]])
# 制御の重み行列
Q = np.eye(2)
R = np.eye(1)
# 無限時間のリカッチ方程式を解く
P = solve_discrete_are(A, B, Q, R)
K = np.linalg.inv(R + B.T @ P @ B) @ (B.T @ P @ A)
# シミュレーションの設定
N = 50 # 時間ステップ数
x = np.zeros((2, N+1))
u = np.zeros((1, N))
y = np.zeros((1, N))
x[:, 0] = [1.0, 0.0] # 初期状態
# システムのシミュレーション
for k in range(N):
u[:, k] = -K @ x[:, k]
x[:, k+1] = A @ x[:, k] + B @ u[:, k]
y[:, k] = C @ x[:, k]
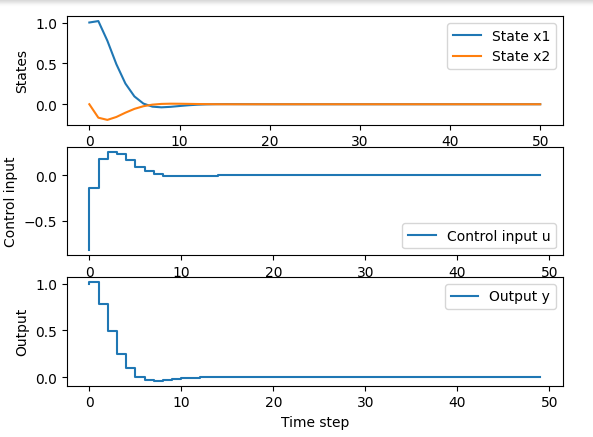
# 結果のプロット
plt.figure()
plt.subplot(3, 1, 1)
plt.plot(range(N+1), x[0, :], label='State x1')
plt.plot(range(N+1), x[1, :], label='State x2')
plt.ylabel('States')
plt.legend()
plt.subplot(3, 1, 2)
plt.step(range(N), u[0, :], label='Control input u')
plt.ylabel('Control input')
plt.legend()
plt.subplot(3, 1, 3)
plt.step(range(N), y[0, :], label='Output y')
plt.ylabel('Output')
plt.legend()
plt.xlabel('Time step')
plt.show()
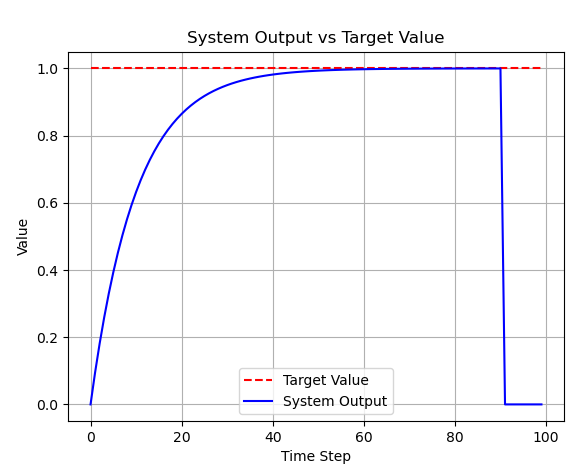
import numpy as np
import matplotlib.pyplot as plt
# プラントパラメータ
A = 1.0
B = 1.0
C = 1.0
D = 0.0
# 制御目標
r = 1.0 # 目標値
N = 10 # 予測ホライズン
T = 50 # シミュレーションステップ数
# MPCパラメータ
Q = 1.0 # 重み行列
R = 0.1 # 重み行列
# 初期化
x = 0.0
u = 0.0
y = 0.0
u_hist = []
y_hist = []
# 参照軌道
ref_trajectory = np.linspace(0, r, N)
for t in range(T):
# 予測誤差計算
error = ref_trajectory - y
# MPC制御則
BQ = B * Q
u_opt = (BQ / (R + B * BQ)) * (ref_trajectory - A * x)
# 入力変化量
delta_u = u_opt - u
u = u + delta_u
# プラント出力計算
y = A * x + B * u
x = y # 状態更新
# 結果記録
u_hist.append(u)
y_hist.append(y)
# 参照軌道更新
ref_trajectory = np.roll(ref_trajectory, -1)
ref_trajectory[-1] = r
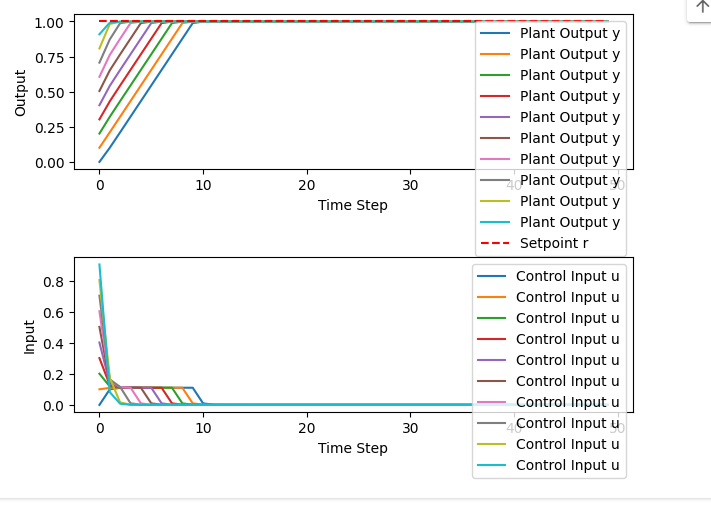
# プロット
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(y_hist, label='Plant Output y')
plt.plot([r]*T, 'r--', label='Setpoint r')
plt.xlabel('Time Step')
plt.ylabel('Output')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(u_hist, label='Control Input u')
plt.xlabel('Time Step')
plt.ylabel('Input')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Parameters initialization
n_iter = 50 # Number of iterations
true_value = 10 # True value (constant)
z = true_value + np.random.normal(0, 1, n_iter) # Observations (adding noise)
# Initial estimate
x_hat = np.zeros(n_iter) # Initialize state estimates
x_hat[0] = 0.0 # Initial state estimate
# Initialize estimate uncertainty
P = np.zeros(n_iter) # Initialize estimate uncertainty
P[0] = 1.0 # Initial estimate uncertainty
# Measurement uncertainty
R = 1.0 # Measurement uncertainty
# Kalman filter execution
for k in range(1, n_iter):
# Prediction step
x_hat[k] = x_hat[k-1] # State prediction
P[k] = P[k-1] # Uncertainty prediction
# Update step
K = P[k] / (P[k] + R) # Compute Kalman gain
x_hat[k] = x_hat[k] + K * (z[k] - x_hat[k]) # State update
P[k] = (1 - K) * P[k] # Uncertainty update
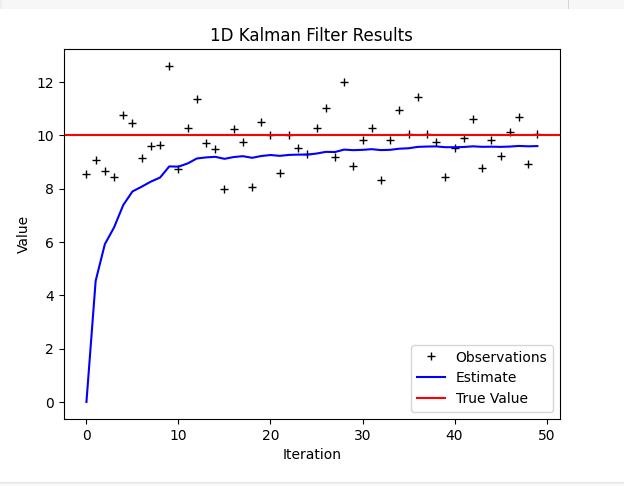
# Plotting results
plt.figure()
plt.plot(z, 'k+', label='Observations')
plt.plot(x_hat, 'b-', label='Estimate')
plt.axhline(true_value, color='r', label='True Value')
plt.legend()
plt.xlabel('Iteration')
plt.ylabel('Value')
plt.title('1D Kalman Filter Results')
plt.show()
# システム行列 A, B
A = np.array([[0, 1],
[-1, -1]])
B = np.array([[0],
[1]])
# リアプノフ関数の重み行列 P (正定値対称行列)
P = np.array([[1, 0],
[0, 1]])
# 安定化ゲイン alpha
alpha = 1
# シミュレーション時間
T = 10
dt = 0.01
time = np.arange(0, T, dt)
# 状態と入力の初期値
x = np.array([1, 1]) # 初期状態ベクトル
u = 0 # 初期入力
# 結果の保存用
x_history = np.zeros((len(time), 2))
# シミュレーション
for i in range(len(time)):
# 状態更新
x_history[i] = x
# リアプノフ関数の微分
V_dot = 2 * np.dot(np.dot(x.T, P), (np.dot(A, x) + np.dot(B, u)))
# 制御入力計算
u = -np.dot(np.linalg.inv(B.T @ P @ B + alpha * np.eye(1)), B.T @ P @ A @ x)
# 状態更新
x = x + dt * (A @ x + B @ u)
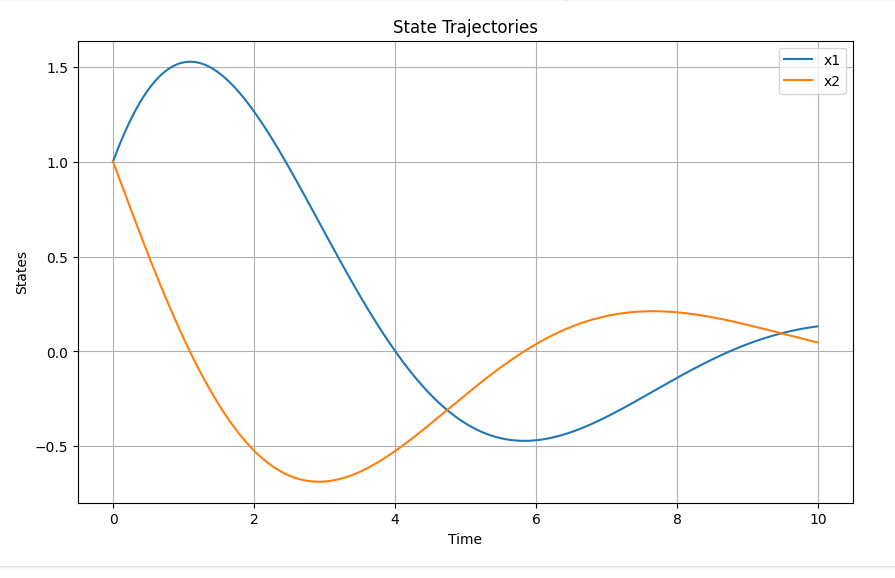
# 結果のプロット
plt.figure(figsize=(10, 6))
plt.plot(time, x_history[:, 0], label='x1')
plt.plot(time, x_history[:, 1], label='x2')
plt.xlabel('Time')
plt.ylabel('States')
plt.title('State Trajectories')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import gym
from gym import spaces
class SimpleSystemEnv(gym.Env):
def __init__(self):
super(SimpleSystemEnv, self).__init__()
self.observation_space = spaces.Box(low=-np.inf, high=np.inf, shape=(2,), dtype=np.float32)
self.action_space = spaces.Discrete(3) # Actions: -1, 0, 1 (change control parameter)
self.state = np.array([0.0, 0.0])
self.control_param = 0.5 # Initial control parameter
self.reference_model = lambda t: np.sin(t) # Reference model (sine wave)
def step(self, action):
t = self.state[0]
error = self.state[1]
reference = self.reference_model(t)
# Update control parameter based on action
if action == 0:
self.control_param -= 0.01
elif action == 2:
self.control_param += 0.01
# Simple system dynamics
control_signal = self.control_param * error
next_error = reference - control_signal
self.state = np.array([t + 0.1, next_error])
reward = -np.abs(next_error) # Reward is negative absolute error
done = t >= 10.0 # Episode ends after 10 seconds
return self.state, reward, done, {}
def reset(self):
self.state = np.array([0.0, 0.0])
return self.state
def render(self, mode='human'):
pass
env = SimpleSystemEnv()
# Q-learning parameters
alpha = 0.1 # Learning rate
gamma = 0.99 # Discount factor
epsilon = 0.1 # Exploration rate
q_table = np.zeros((200, 3)) # Q-table initialization
def discretize_state(state):
t_discrete = int(state[0] * 10) # Discretize time
error_discrete = int((state[1] + 1) * 100) # Discretize error
return t_discrete, error_discrete
# Training loop
for episode in range(1000):
state = env.reset()
total_reward = 0
done = False
while not done:
t_discrete, error_discrete = discretize_state(state)
if np.random.uniform(0, 1) < epsilon:
action = env.action_space.sample() # Exploration
else:
action = np.argmax(q_table[t_discrete, :]) # Exploitation
next_state, reward, done, _ = env.step(action)
next_t_discrete, next_error_discrete = discretize_state(next_state)
q_table[t_discrete, action] += alpha * (reward + gamma * np.max(q_table[next_t_discrete, :]) - q_table[t_discrete, action])
state = next_state
total_reward += reward
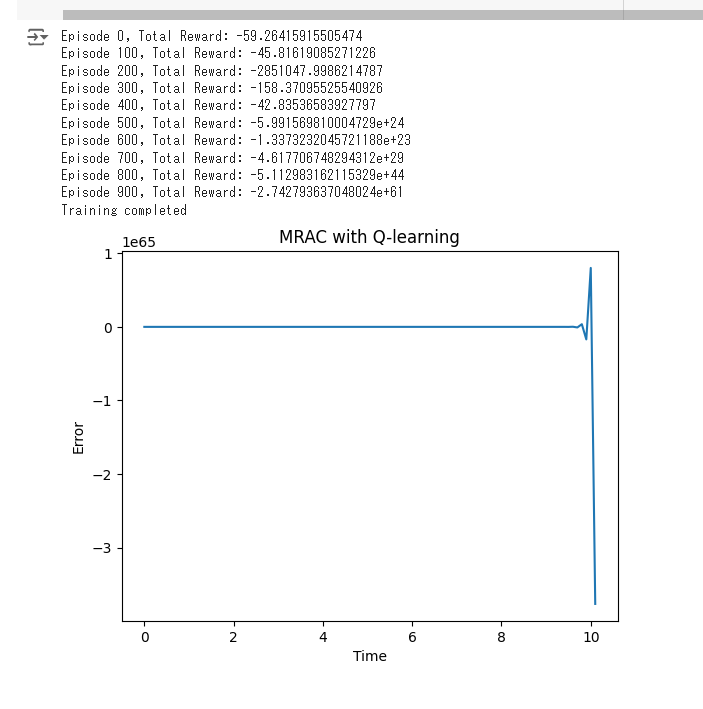
if episode % 100 == 0:
print(f"Episode {episode}, Total Reward: {total_reward}")
print("Training completed")
# Test the trained policy
state = env.reset()
done = False
states = []
while not done:
t_discrete, error_discrete = discretize_state(state)
action = np.argmax(q_table[t_discrete, :])
next_state, _, done, _ = env.step(action)
states.append(state)
state = next_state
# Plot results
states = np.array(states)
time = states[:, 0]
errors = states[:, 1]
plt.plot(time, errors)
plt.xlabel('Time')
plt.ylabel('Error')
plt.title('MRAC with Q-learning')
plt.show()
import numpy as np
import gym
import matplotlib.pyplot as plt
class AdaptiveFeedbackControlEnv(gym.Env):
def __init__(self):
super(AdaptiveFeedbackControlEnv, self).__init__()
self.observation_space = spaces.Box(low=-np.inf, high=np.inf, shape=(2,), dtype=np.float32)
self.action_space = spaces.Discrete(3) # Actions: -1, 0, 1 (change control parameter)
self.state = np.array([0.0, 0.0])
self.control_param = 0.5 # Initial control parameter
self.reference_model = lambda t: np.sin(t) # Reference model (sine wave)
def step(self, action):
t = self.state[0]
error = self.state[1]
reference = self.reference_model(t)
# Simulate noise affecting the system (example: random noise)
noise = np.random.normal(loc=0, scale=0.1)
error_with_noise = error + noise
# Update control parameter based on action
if action == 0:
self.control_param -= 0.01
elif action == 2:
self.control_param += 0.01
# Simple system dynamics with noise
control_signal = self.control_param * error_with_noise
next_error = reference - control_signal
self.state = np.array([t + 0.1, next_error])
reward = -np.abs(next_error) # Reward is negative absolute error
done = t >= 10.0 # Episode ends after 10 seconds
return self.state, reward, done, {"control_signal": control_signal, "reference": reference, "error": next_error}
def reset(self):
self.state = np.array([0.0, 0.0])
return self.state
def render(self, mode='human'):
pass
env = AdaptiveFeedbackControlEnv()
states = []
control_signals = []
references = []
errors = []
state = env.reset()
done = False
while not done:
action = env.action_space.sample() # Random action
state, reward, done, info = env.step(action)
states.append(state)
control_signals.append(info['control_signal'])
references.append(info['reference'])
errors.append(info['error'])
times = np.arange(0, len(states) * 0.1, 0.1)
states = np.array(states)
control_signals = np.array(control_signals)
references = np.array(references)
errors = np.array(errors)
plt.figure(figsize=(12, 8))
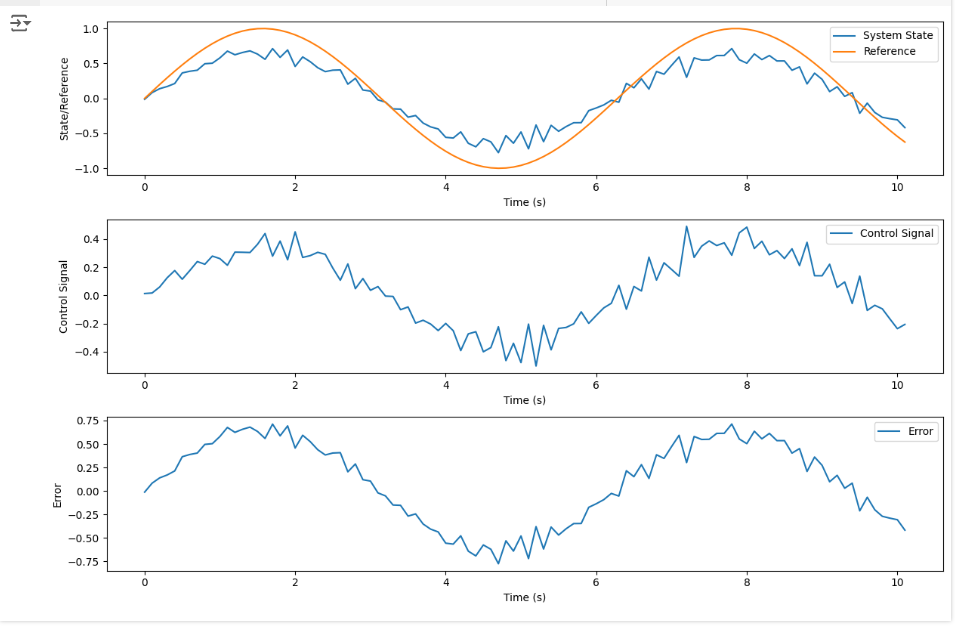
plt.subplot(3, 1, 1)
plt.plot(times, states[:, 1], label='System State')
plt.plot(times, references, label='Reference')
plt.xlabel('Time (s)')
plt.ylabel('State/Reference')
plt.legend()
plt.subplot(3, 1, 2)
plt.plot(times, control_signals, label='Control Signal')
plt.xlabel('Time (s)')
plt.ylabel('Control Signal')
plt.legend()
plt.subplot(3, 1, 3)
plt.plot(times, errors, label='Error')
plt.xlabel('Time (s)')
plt.ylabel('Error')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.linalg import solve_continuous_are
# システム行列の定義
A1 = np.array([[1.0, 2.0], [-3.0, -4.0]])
A2 = np.array([[0.5, 1.5], [-2.0, -3.5]])
# 任意の対称正定値行列 Q を定義
Q = np.eye(2)
# A1とA2に共通のリアプノフ行列を求める関数
def solve_common_lyapunov(A1, A2, Q):
P1 = solve_continuous_are(A1.T, np.eye(A1.shape[0]), Q, np.eye(A1.shape[0]))
P2 = solve_continuous_are(A2.T, np.eye(A2.shape[0]), Q, np.eye(A2.shape[0]))
P = 0.5 * (P1 + P2)
return P
# 共通リアプノフ行列を計算
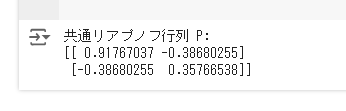
P = solve_common_lyapunov(A1, A2, Q)
print("共通リアプノフ行列 P:")
print(P)
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
dt = 1.0 # タイムステップ
sigma_a = 0.1 # 加速度の標準偏差
sigma_z = 0.1 # 観測誤差の標準偏差
n_steps = 50 # シミュレーションのステップ数
# システム行列
F = np.array([[1, dt], [0, 1]])
G = np.array([[0.5 * dt**2], [dt]])
H = np.array([[1, 0]])
# 共分散行列
Q = sigma_a**2 * np.array([[0.25 * dt**4, 0.5 * dt**3], [0.5 * dt**3, dt**2]])
R = np.array([[sigma_z**2]])
# 初期条件
x = np.array([[0], [0]]) # 初期状態
P = np.zeros((2, 2)) # 初期誤差共分散行列
# カルマンフィルターの結果を保存するリスト
x_estimated = []
x_true = []
z_measurements = []
# シミュレーション
for k in range(n_steps):
# 真の状態更新
a = np.random.normal(0, sigma_a)
w = G * a
x = F @ x + w
x_true.append(x.flatten())
# 観測値
v = np.random.normal(0, sigma_z)
z = H @ x + v
z_measurements.append(z.flatten())
# 予測ステップ
x_pred = F @ x
P_pred = F @ P @ F.T + Q
# 更新ステップ
y = z - H @ x_pred # 観測残差
S = H @ P_pred @ H.T + R # 残差の共分散
K = P_pred @ H.T @ np.linalg.inv(S) # カルマンゲイン
x = x_pred + K @ y
P = (np.eye(2) - K @ H) @ P_pred
x_estimated.append(x.flatten())
# 結果のプロット
x_true = np.array(x_true)
x_estimated = np.array(x_estimated)
z_measurements = np.array(z_measurements)
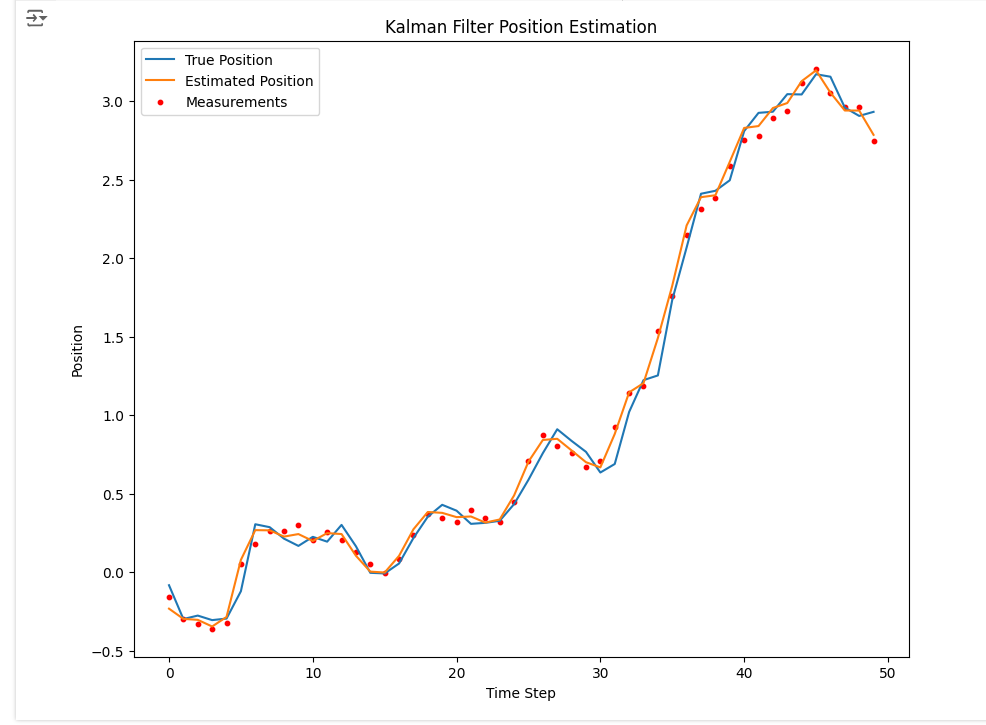
plt.figure(figsize=(10, 8))
plt.plot(x_true[:, 0], label='True Position')
plt.plot(x_estimated[:, 0], label='Estimated Position')
plt.scatter(range(n_steps), z_measurements[:, 0], label='Measurements', color='red', s=10)
plt.xlabel('Time Step')
plt.ylabel('Position')
plt.legend()
plt.title('Kalman Filter Position Estimation')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Parameter settings
T = 0.001 # Sampling period
N = 1000 # Number of simulation steps
prediction_horizon = 20 # Prediction horizon
control_horizon = 5 # Control horizon
s = 1 # Scale of the reference value
tau = 0.1 # Time constant of the reference trajectory
# Weight matrices
Q = 1 # Weight for the output
R = 0.1 # Weight for the input change
# Initialize the discrete integrator
x = 0
y = np.zeros(N)
u = np.zeros(N)
r = np.zeros(N)
# Generate the reference trajectory
for k in range(1, N):
r[k] = s * (1 - np.exp(-k * T / tau))
# Cost function for MPC
def cost_function(U, *args):
y_pred, x0, ref = args
cost = 0
x = x0
for k in range(len(U)):
x = x + U[k]
y_pred[k] = x
cost += Q * (y_pred[k] - ref[k]) ** 2 + R * U[k] ** 2
return cost
# Simulate the system
for k in range(N - prediction_horizon):
# Predict future outputs
y_pred = np.zeros(prediction_horizon)
# Solve the optimization problem
u_initial_guess = np.zeros(control_horizon)
bounds = [(-1, 1)] * control_horizon
res = minimize(cost_function, u_initial_guess, args=(y_pred, x, r[k:k+prediction_horizon]), bounds=bounds)
# Apply the first control input
u[k] = res.x[0]
# Update the state
x = x + u[k]
y[k] = x
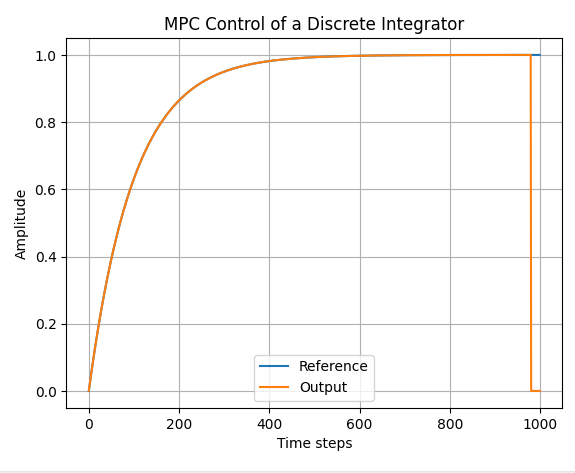
# Plot the results
plt.figure()
plt.plot(r, label='Reference')
plt.plot(y, label='Output')
plt.xlabel('Time steps')
plt.ylabel('Amplitude')
plt.legend()
plt.title('MPC Control of a Discrete Integrator')
plt.grid(True)
plt.show()
import numpy as np
# パラメータ推定のためのデータセット
# 例として、xとyのデータが与えられたとします
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.1, 3.9, 6.2, 8.1, 9.8])
# データセットの行列形式
X = np.vstack([np.ones_like(x), x]).T
# データ数
n = len(x)
# 重み行列Wの設定(ここでは単位行列を使用)
W = np.eye(n)
# 最小二乗推定値の計算
theta_hat = np.linalg.inv(X.T @ W @ X) @ X.T @ W @ y
# 評価関数の計算
J = np.sum(W * (y - X @ theta_hat)**2)
# ヘッセ行列の計算(2次形式の係数行列)
Hessian = X.T @ W @ X
# ヘッセ行列が正定値かどうかの確認
is_positive_definite = np.all(np.linalg.eigvals(Hessian) > 0)
# 勾配ベクトルの計算
gradient = -2 * X.T @ W @ (y - X @ theta_hat)
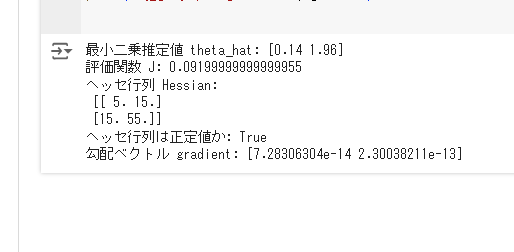
# 結果の出力
print("最小二乗推定値 theta_hat:", theta_hat)
print("評価関数 J:", J)
print("ヘッセ行列 Hessian:\n", Hessian)
print("ヘッセ行列は正定値か:", is_positive_definite)
print("勾配ベクトル gradient:", gradient)
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# ダミー入力信号の生成(例としてsin波を使う)
t = np.linspace(0, 10, 1000)
input_signal = np.sin(2 * np.pi * t)
# ARMAモデルのパラメータ
order_ar = 2 # AR次数
order_ma = 1 # MA次数
# ARMAモデルの生成
ar_params = np.array([0.5, -0.2]) # AR係数
ma_params = np.array([0.3]) # MA係数
arma_process = ArmaProcess(ar_params, ma_params)
# 入力信号にARMAモデルを適用
arma_signal = arma_process.generate_sample(nsample=len(input_signal))
# 自己相関関数と偏自己相関関数のプロット
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
plot_acf(arma_signal, ax=ax1, title='Autocorrelation Function (ACF)')
plot_pacf(arma_signal, ax=ax2, title='Partial Autocorrelation Function (PACF)')
plt.tight_layout()
plt.show()
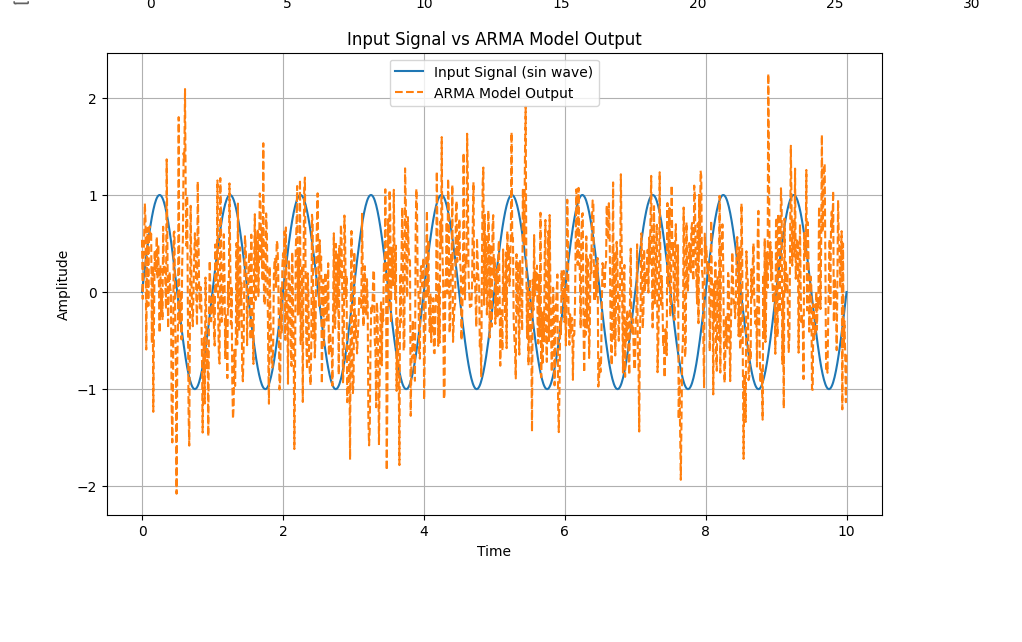
# プロットを使った入力信号とARMAモデルの比較
plt.figure(figsize=(10, 6))
plt.plot(t, input_signal, label='Input Signal (sin wave)')
plt.plot(t, arma_signal, label='ARMA Model Output', linestyle='--')
plt.title('Input Signal vs ARMA Model Output')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate
# M系列信号生成関数
def m_sequence(n):
# M系列のレジスタ初期値
register = np.array([1, 0, 0, 0, 0, 0, 0, 1])
sequence = []
for _ in range(n):
sequence.append(register[-1])
new_bit = register[0] ^ register[7] # XORの結果を計算
register = np.roll(register, -1) # レジスタを1ビット左にシフト
register[-1] = new_bit # 新しいビットをレジスタに追加
return np.array(sequence)
# M系列信号の長さ
n = 1000
m_seq = m_sequence(n)
# 自己相関関数の計算
acf = correlate(m_seq, m_seq, mode='full') / n
# SN比の計算(パワー比)
signal_power = np.sum(m_seq ** 2) / n
noise_power = np.sum((m_seq - np.mean(m_seq)) ** 2) / n
snr = 10 * np.log10(signal_power / noise_power)
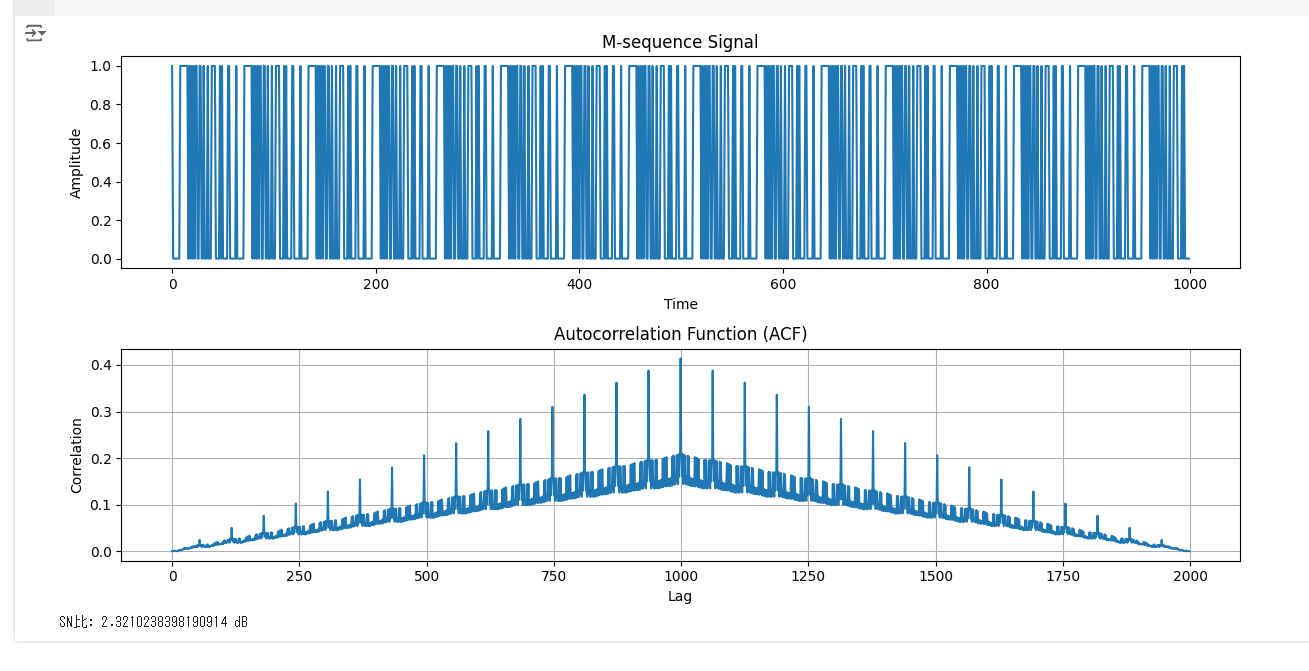
# プロット:M系列信号と自己相関関数
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(m_seq)
plt.title('M-sequence Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.subplot(2, 1, 2)
plt.plot(acf)
plt.title('Autocorrelation Function (ACF)')
plt.xlabel('Lag')
plt.ylabel('Correlation')
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"SN比: {snr} dB")
import numpy as np
import matplotlib.pyplot as plt
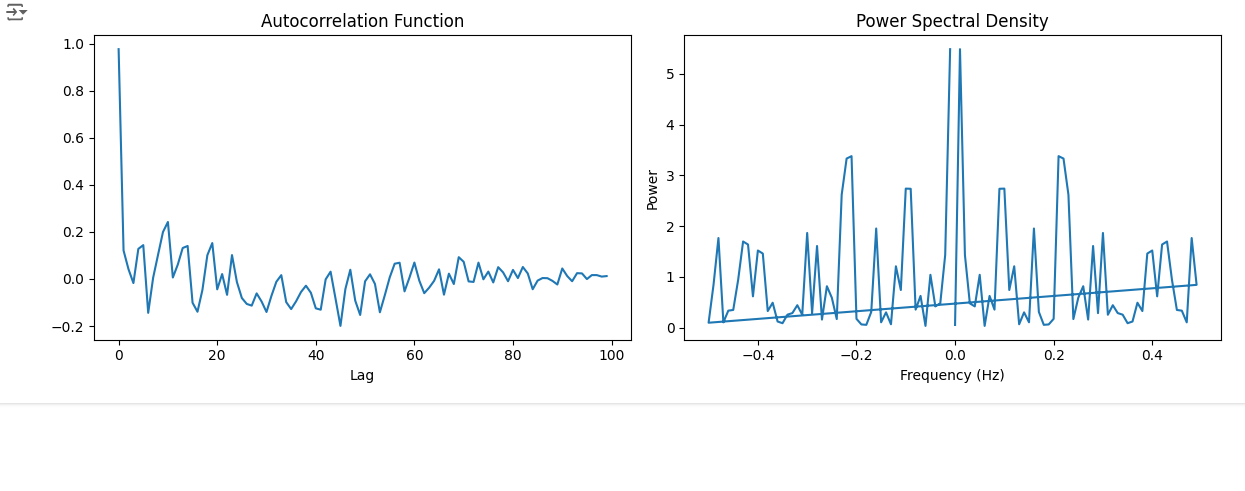
def autocorrelation(signal):
n = len(signal)
auto_corr = np.correlate(signal, signal, mode='full') / n
return auto_corr[n-1:]
def power_spectrum(signal, fs):
freqs = np.fft.fftfreq(len(signal), d=1/fs)
psd = np.abs(np.fft.fft(signal))**2 / len(signal)
return freqs, psd
# 離散時間信号の生成
signal = np.random.randn(100)
# サンプリング周波数
fs = 1 # 1 Hz
# 自己相関関数とパワースペクトル密度関数の計算
auto_corr = autocorrelation(signal)
freqs, psd = power_spectrum(signal, fs)
# プロット
plt.figure(figsize=(12, 4))
# 自己相関関数のプロット
plt.subplot(121)
plt.plot(auto_corr)
plt.title('Autocorrelation Function')
plt.xlabel('Lag')
# パワースペクトル密度関数のプロット
plt.subplot(122)
plt.plot(freqs, psd)
plt.title('Power Spectral Density')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power')
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from sklearn.linear_model import LinearRegression
# システムの定義
def system(y, t, u, Kp, Ki, Kd, setpoint):
e = setpoint - y[0] # 誤差
integral = y[1] # 積分項
derivative = y[2] # 微分項
dydt = [Kp*e + Ki*integral + Kd*derivative, e, y[0]]
return dydt
# システムシミュレーション
def simulate_system(Kp, Ki, Kd, setpoint, disturbance):
t = np.linspace(0, 10, 1000)
y0 = [0, 0, 0] # 初期条件
u = 0
y = odeint(system, y0, t, args=(u, Kp, Ki, Kd, setpoint))
# 外乱を加える
disturbance_signal = disturbance * np.sin(0.1 * np.pi * t)
y[:, 0] += disturbance_signal
return t, y[:, 0]
# データ生成
def generate_data(num_samples):
X = []
y = []
setpoint = 1.0
disturbance = 0.2
for _ in range(num_samples):
Kp = np.random.uniform(0.5, 2.0)
Ki = np.random.uniform(0.1, 1.0)
Kd = np.random.uniform(0.05, 0.5)
t, output = simulate_system(Kp, Ki, Kd, setpoint, disturbance)
error = setpoint - output
mse = np.mean(error**2)
X.append([Kp, Ki, Kd])
y.append(mse)
return np.array(X), np.array(y)
# ゲインのチューニング(機械学習)
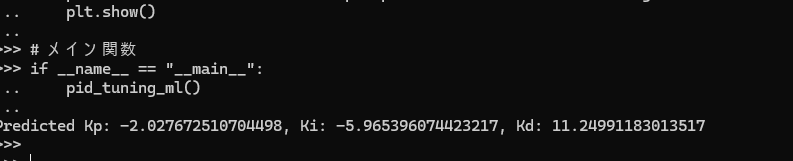
def pid_tuning_ml():
X, y = generate_data(100)
model = LinearRegression()
model.fit(X, y)
# 最適なゲインの予測
Kp, Ki, Kd = model.coef_
print(f"Predicted Kp: {Kp}, Ki: {Ki}, Kd: {Kd}")
setpoint = 1.0
disturbance = 0.2
t, output = simulate_system(Kp, Ki, Kd, setpoint, disturbance)
plt.plot(t, output, label='Output')
plt.axhline(y=setpoint, color='r', linestyle='--', label='Setpoint')
plt.xlabel('Time')
plt.ylabel('Output')
plt.legend()
plt.title('PID Control with Step Input and Disturbance (ML Tuning)')
plt.show()
# メイン関数
if __name__ == "__main__":
pid_tuning_ml()
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
# Continuous-time transfer function coefficients
b0, b1, b2 = 1, 2, 3 # Example coefficients
a0, a1, a2 = 4, 5, 6 # Example coefficients
# Convert transfer function to state-space model
A, B, C, D = signal.tf2ss([b0, b1, b2], [a0, a1, a2])
# Sampling period
T = 0.1 # Example sampling period
# Discretize the system using Tustin (bilinear) transform
system_discrete = signal.cont2discrete((A, B, C, D), T, method='bilinear')
A_d, B_d, C_d, D_d, dt = system_discrete
print("Continuous-time state-space model")
print("A:", A)
print("B:", B)
print("C:", C)
print("D:", D)
print("\nDiscrete-time state-space model")
print("A:", A_d)
print("B:", B_d)
print("C:", C_d)
print("D:", D_d)
print("Sampling period:", dt)
# Simulation of the discrete-time model
# Plot the step response
time_steps = 100 # Number of time steps
u = np.ones(time_steps)
_, y_out, _ = signal.dlsim((A_d, B_d, C_d, D_d, dt), u)
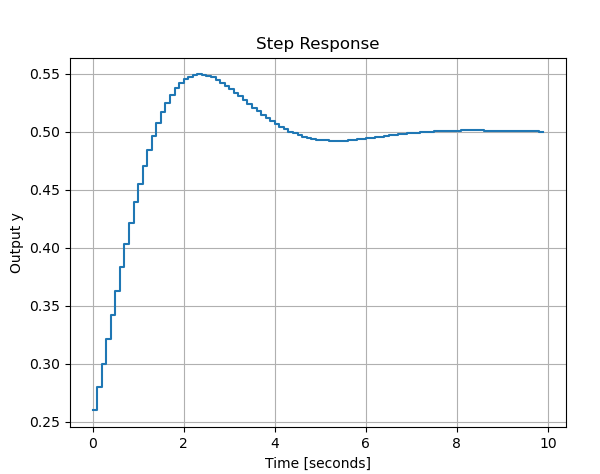
plt.figure()
plt.step(np.arange(time_steps) * T, y_out, where='post')
plt.xlabel('Time [seconds]')
plt.ylabel('Output y')
plt.title('Step Response')
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from sklearn.linear_model import LinearRegression
# ますばねダンパーのパラメータ
m = 1.0 # 質量
c = 0.5 # 減衰係数
k = 2.0 # バネ定数
# 外力
def external_force(t):
return np.sin(t)
# 微分方程式
def mass_spring_damper(t, y):
x, v = y
F = external_force(t)
dxdt = v
dvdt = (F - c * v - k * x) / m
return [dxdt, dvdt]
# 初期条件
y0 = [0.0, 0.0] # 初期変位と初速度
# シミュレーション時間
t_span = (0, 20)
t_eval = np.linspace(*t_span, 1000)
# シミュレーション実行
sol = solve_ivp(mass_spring_damper, t_span, y0, t_eval=t_eval)
# シミュレーション結果のプロット
plt.figure(figsize=(10, 5))
plt.plot(sol.t, sol.y[0], label='Position (x)')
plt.plot(sol.t, sol.y[1], label='Velocity (v)')
plt.xlabel('Time (s)')
plt.ylabel('Value')
plt.title('Mass-Spring-Damper System')
plt.legend()
plt.grid()
plt.show()
# 機械学習によるパラメータ調整
# データ生成
X = np.column_stack((sol.y[0], sol.y[1])) # 変位と速度を特徴量として使用
y = external_force(sol.t) # 外力をターゲットとして使用
# モデルのトレーニング
model = LinearRegression()
model.fit(X, y)
# モデルの係数と切片
k_pred, c_pred = model.coef_
F_pred = model.intercept_
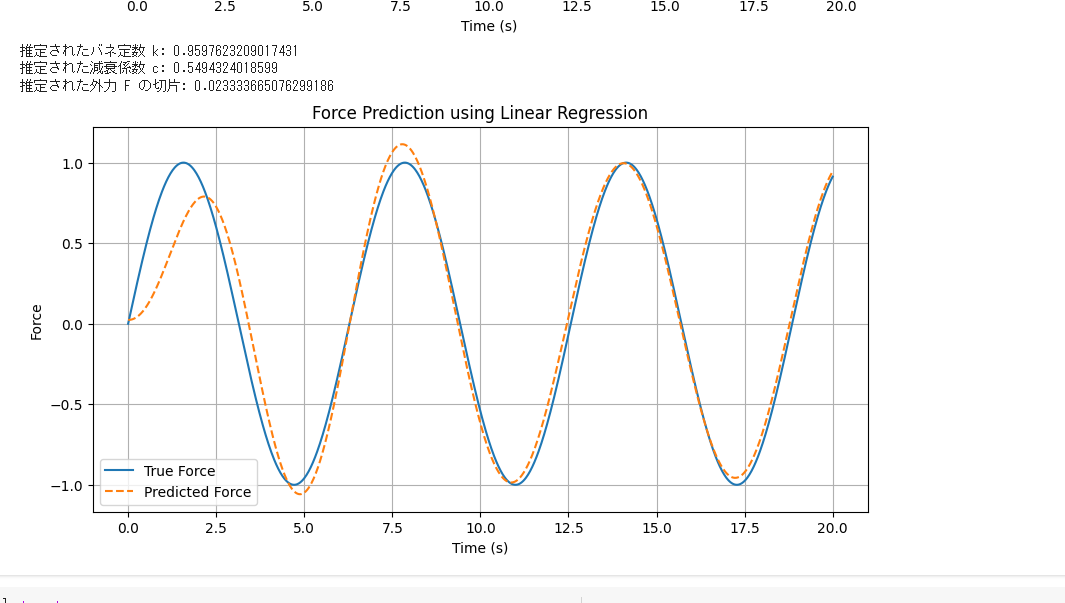
print(f"推定されたバネ定数 k: {k_pred}")
print(f"推定された減衰係数 c: {c_pred}")
print(f"推定された外力 F の切片: {F_pred}")
# 推定されたモデルによる予測
y_pred = model.predict(X)
# 結果のプロット
plt.figure(figsize=(10, 5))
plt.plot(sol.t, y, label='True Force')
plt.plot(sol.t, y_pred, label='Predicted Force', linestyle='--')
plt.xlabel('Time (s)')
plt.ylabel('Force')
plt.title('Force Prediction using Linear Regression')
plt.legend()
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
dt = 1.0 # 時間ステップ(秒)
total_time = 100 # シミュレーション時間(秒)
time = np.arange(0, total_time, dt)
# 真の軌道パラメータ
x_true = 7000.0 # 初期位置 x (km)
y_true = 0.0 # 初期位置 y (km)
vx_true = 0.0 # 初期速度 vx (km/s)
vy_true = 7.5 # 初期速度 vy (km/s)
# 状態ベクトル [x, y, vx, vy]
state_true = np.array([x_true, y_true, vx_true, vy_true])
# 状態遷移行列
F = np.array([[1, 0, dt, 0],
[0, 1, 0, dt],
[0, 0, 1, 0],
[0, 0, 0, 1]])
# 観測行列
H = np.array([[1, 0, 0, 0],
[0, 1, 0, 0]])
# 観測ノイズの共分散
R = np.diag([100.0, 100.0]) # 観測ノイズの標準偏差を10kmと仮定
# 真の軌道を生成(単純な円軌道を仮定)
true_positions = []
for t in time:
true_positions.append(state_true[:2])
state_true = F @ state_true
true_positions = np.array(true_positions)
# ノイズ付き観測データを生成
observed_positions = true_positions + np.random.multivariate_normal([0, 0], R, len(time))
# カルマンフィルタの初期化
state_est = np.array([x_true, y_true, vx_true, vy_true])
P = np.diag([1000.0, 1000.0, 10.0, 10.0]) # 初期共分散行列
Q = np.diag([0.1, 0.1, 0.1, 0.1]) # プロセスノイズの共分散行列
# 推定された位置を保存するリスト
estimated_positions = []
for t in range(len(time)):
# 時間更新(予測ステップ)
state_est = F @ state_est
P = F @ P @ F.T + Q
# 観測更新(更新ステップ)
z = observed_positions[t]
y = z - H @ state_est
S = H @ P @ H.T + R
K = P @ H.T @ np.linalg.inv(S)
state_est = state_est + K @ y
P = (np.eye(4) - K @ H) @ P
# 推定された位置を保存
estimated_positions.append(state_est[:2])
estimated_positions = np.array(estimated_positions)
# 結果のプロット
plt.figure(figsize=(10, 8))
plt.plot(true_positions[:, 0], true_positions[:, 1], label='True Orbit', color='g')
plt.scatter(observed_positions[:, 0], observed_positions[:, 1], label='Observed Position', color='r', s=10)
plt.plot(estimated_positions[:, 0], estimated_positions[:, 1], label='Estimated Orbit', color='b')
plt.xlabel('X position (km)')
plt.ylabel('Y position (km)')
plt.legend()
plt.title('Orbit Estimation using Kalman Filter')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_continuous_are
# 振子のパラメータ
m = 1.0 # 振子の質量 [kg]
l = 1.0 # 振子の長さ [m]
g = 9.81 # 重力加速度 [m/s^2]
# 状態空間モデル
A = np.array([[0, 1],
[-g/l, 0]])
B = np.array([[0],
[1/(m*l**2)]])
C = np.array([[1, 0]])
# 重み行列の設定
Q = np.diag([1, 1]) # 状態の重み行列
R = np.array([[1]]) # 入力の重み行列
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 状態フィードバックゲインを計算
K = np.dot(np.dot(np.linalg.inv(R), B.T), P)
# 初期条件
theta0 = np.pi / 4.0
theta_dot0 = 0.0
x0 = np.array([[theta0], [theta_dot0]])
# シミュレーションパラメータ
dt = 0.02
t_end = 5.0
time = np.arange(0, t_end, dt)
steps = len(time)
# シミュレーション
x_hist = np.zeros((2, steps))
x_hist[:, 0] = x0.flatten()
u_hist = np.zeros(steps)
for i in range(1, steps):
u = -np.dot(K, x_hist[:, i-1]) # 状態フィードバック制御入力
u_hist[i] = u # 制御入力の記録
# 状態方程式の更新
x_dot = np.dot(A, x_hist[:, i-1]) + np.dot(B, u)
x_hist[:, i] = x_hist[:, i-1] + x_dot * dt
# 結果のプロット
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(time, x_hist[0, :], label='Pendulum Angle')
plt.xlabel('Time (s)')
plt.ylabel('Angle (rad)')
plt.title('Pendulum Angle Control with State Feedback')
plt.legend()
plt.grid(True)
plt.subplot(3, 1, 2)
plt.plot(time, x_hist[1, :], label='Angular Velocity')
plt.xlabel('Time (s)')
plt.ylabel('Angular Velocity (rad/s)')
plt.title('Pendulum Angular Velocity')
plt.legend()
plt.grid(True)
plt.subplot(3, 1, 3)
plt.plot(time, u_hist, label='Control Input (Force)')
plt.xlabel('Time (s)')
plt.ylabel('Control Input (Force)')
plt.title('Control Input (Force) over Time')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# System parameters
T = 0.1 # Sampling period
tau = 1.0 # Time constant
# Prediction horizon and control horizon
N_pred = 10
N_ctrl = 3
# Constraints
u_min = -1.0
u_max = 1.0
# System model
A = np.exp(-T/tau)
B = (1 - np.exp(-T/tau))
# Target value
r = np.ones(100) # Step input
# State vector initialization
x = np.zeros(100)
u = np.zeros(100)
# Function to compute optimal input
def cost_function(U, x0, r, N_pred, N_ctrl, A, B):
x = x0
cost = 0
for k in range(N_pred):
if k < N_ctrl:
u = U[k]
else:
u = U[N_ctrl-1]
x = A * x + B * u
cost += (x - r[k])**2
return cost
# MPC control loop
for k in range(len(r)-N_pred):
# Set up the optimization problem
U0 = np.zeros(N_ctrl) # Initial guess for inputs
bounds = [(u_min, u_max)] * N_ctrl
result = minimize(cost_function, U0, args=(x[k], r[k:k+N_pred], N_pred, N_ctrl, A, B), bounds=bounds)
u[k] = result.x[0]
# Update the system
x[k+1] = A * x[k] + B * u[k]
# Plot results separately
# Plot target value and system output
plt.figure()
plt.plot(r, 'r--', label='Target Value')
plt.plot(x, 'b-', label='System Output')
plt.xlabel('Time Step')
plt.ylabel('Value')
plt.legend()
plt.title('System Output vs Target Value')
plt.grid(True)
plt.show()
# Plot control input
plt.figure()
plt.step(np.arange(len(u)), u, 'g-', where='post', label='Control Input')
plt.xlabel('Time Step')
plt.ylabel('Control Input')
plt.legend()
plt.title('Control Input Over Time')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# 行列の定義
A = np.array([[1, 2],
[3, 4]])
# 固有値と固有ベクトルの計算
eigenvalues, eigenvectors = np.linalg.eig(A)
print("固有値:", eigenvalues)
print("固有ベクトル:", eigenvectors)
# 状態遷移行列の定義
def plot_phase_portrait(A):
# グリッドを作成
x1, x2 = np.meshgrid(np.linspace(-10, 10, 20), np.linspace(-10, 10, 20))
dx1, dx2 = np.dot(A, np.vstack([x1.ravel(), x2.ravel()]))
dx1 = dx1.reshape(x1.shape)
dx2 = dx2.reshape(x2.shape)
# 位相面図の描画
plt.figure(figsize=(8, 6))
plt.quiver(x1, x2, dx1, dx2, angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Phase Portrait')
plt.grid()
plt.sho
w()
# 位相面図を描画
plot_phase_portrait(A)
import numpy as np
from scipy.linalg import solve_continuous_are
import matplotlib.pyplot as plt
# 状態遷移行列 A と正定値行列 Q の定義
A = np.array([[1, 2],
[3, 4]])
Q = np.eye(2) # 正定値行列として単位行列を使用
# リアプノフ方程式を解く
P = solve_continuous_are(A, np.eye(2), Q, np.eye(2))
print("リアプノフ行列 P:")
print(P)
# 行列 A の固有値を計算
eigenvalues, _ = np.linalg.eig(A)
print("行列 A の固有値:")
print(eigenvalues)
# 固有値の実部を確認して安定性を判定
if np.all(np.real(eigenvalues) < 0):
print("システムは漸近的に安定です。")
else:
print("システムは漸近的に安定ではありません。")
# 位相面図の描画
def plot_phase_portrait(A):
# グリッドを作成
x1, x2 = np.meshgrid(np.linspace(-10, 10, 20), np.linspace(-10, 10, 20))
dx1, dx2 = np.dot(A, np.vstack([x1.ravel(), x2.ravel()]))
dx1 = dx1.reshape(x1.shape)
dx2 = dx2.reshape(x2.shape)
# 位相面図の描画
plt.figure(figsize=(8, 6))
plt.quiver(x1, x2, dx1, dx2, angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Phase Portrait')
plt.grid()
plt.show()
# 位相面図を描画
plot_phase_portrait(A)
import numpy as np
from scipy.linalg import solve_continuous_are
# システムの定義
A = np.array([[0, 1], [-1, -1]])
B = np.array([[0], [1]])
Q = np.eye(2) # 状態重み行列
R = np.array([[1]]) # 制御重み行列
# 1. 状態フィードバックゲインの計算(極配置法)
poles = np.array([-2, -3])
# Constructing the controllability matrix
P = np.hstack([np.linalg.matrix_power(A, i) @ B for i in range(A.shape[0])])
# Computing the gain matrix (approximate solution)
K = np.linalg.inv(P.T @ P) @ P.T @ np.array(poles).reshape(-1, 1)
print("State Feedback Gain:", K)
# 2. 最適レギュレータの設計
P_opt = solve_continuous_are(A, B, Q, R)
K_opt = np.linalg.inv(R) @ B.T @ P_opt
print("Optimal State Feedback Gain:", K_opt)
# 3. 固有値の計算
eigenvalues, eigenvectors = np.linalg.eig(A)
print("Eigenvalues:", eigenvalues)
# 4. 初期状態の設定
initial_state = np.array([1, 0]) # 例えば、初期状態が[1, 0]
print("Initial State:", initial_state)
# 5. 対角行列の生成
D = np.diag([1, 2])
print("Diagonal Matrix:", D)
# 6. 評価関数の計算
J = np.trace(P_opt @ Q @ P_opt.T) + np.trace(R) # 評価関数の例
print("Cost Function:", J)
# 7. リッカチ方程式の解法
P_riccati = solve_continuous_are(A, B, Q, R)
print("Riccati Solution P:", P_riccati)
# 8. ハミルトン行列の生成
H = np.block([[A, np.zeros_like(A)], [-np.linalg.inv(R) @ B @ B.T @ np.linalg.inv(R) @ A.T, -A.T]])
print("Hamiltonian Matrix:", H)
# 9. 可制御性のチェック
P_controllability = np.hstack([np.linalg.matrix_power(A, i) @ B for i in range(A.shape[0])])
controllability_rank = np.linalg.matrix_rank(P_controllability)
print("Controllability Rank:", controllability_rank)
# 10. 可観測性のチェック
C = np.array([[1, 0]])
O = np.vstack([np.linalg.matrix_power(A.T, i) @ C.T for i in range(A.shape[0])]).T
observability_rank = np.linalg.matrix_rank(O)
print("Observability Rank:", observability_rank)
import numpy as np
from scipy.linalg import solve_continuous_are, svd
# システムの定義
A = np.array([[0, 1], [-1, -1]])
B = np.array([[0], [1]])
C = np.array([[1, 0]])
D = np.array([[0]])
Q = np.eye(2) # 状態重み行列
R = np.array([[1]]) # 制御重み行列
# 1. 状態方程式の定義
# システムの状態方程式は既にA, B, C, Dで定義されています
# 2. 出力フィードバックの設計
P_opt = solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R) @ B.T @ P_opt
print("Output Feedback Gain K:", K)
# 3. オブザーバーの設計(オブザーバ極の配置)
poles_observer = np.array([-5, -6]) # オブザーバ極の指定
# Constructing the controllability matrix
P_observer = np.hstack([np.linalg.matrix_power(A.T, i) @ C.T for i in range(A.shape[0])]).T
# Computing the observer gain matrix
L = np.linalg.inv(P_observer.T @ P_observer) @ P_observer.T @ np.array(poles_observer).reshape(-1, 1)
print("Observer Gain L:", L)
# 4. 外乱オブザーバの設計(外乱推定のための設計)
A_aug = np.block([[A, np.zeros((A.shape[0], 1))], [np.zeros((1, A.shape[0])), np.array([[0]])]])
B_aug = np.block([[B], [np.array([[1]])]])
C_aug = np.block([[C, np.zeros((C.shape[0], 1))]])
L_aug = np.linalg.inv(P_observer.T @ P_observer) @ P_observer.T @ np.array(poles_observer).reshape(-1, 1)
print("Disturbance Observer Gain L_aug:", L_aug)
# 5. 推定値の計算(例としてステップ応答を用いる)
x0 = np.array([1, 0]) # 初期状態
u = np.array([1]) # 入力信号
dt = 0.01 # タイムステップ
t = np.arange(0, 10, dt)
x = np.zeros((len(t), A.shape[0]))
x_hat = np.zeros((len(t), A.shape[0]))
for i in range(1, len(t)):
x[i] = x[i-1] + (A @ x[i-1] + B @ u) * dt
x_hat[i] = x_hat[i-1] + (A @ x_hat[i-1] + B @ u + L @ (C @ (x[i] - x_hat[i-1]))) * dt
print("Estimated State:", x_hat[-1])
import numpy as np
from scipy.linalg import solve_discrete_are
# パラメータの設定
A = np.array([[1, 1], [0, 1]]) # 状態遷移行列
B = np.array([[0.5], [1]]) # 制御行列
C = np.array([[1, 0]]) # 観測行列
Q = np.eye(2) # プロセスノイズ共分散
R = np.eye(1) # 観測ノイズ共分散
# 初期値
x_hat = np.array([0, 0]) # 初期推定状態
P = np.eye(2) # 初期共分散行列
# システムのシミュレーション
np.random.seed(0)
n_steps = 100
true_states = np.zeros((n_steps, 2))
observations = np.zeros(n_steps)
state_noise = np.random.multivariate_normal([0, 0], Q, n_steps)
measurement_noise = np.random.normal(0, np.sqrt(R), n_steps)
for t in range(n_steps):
if t == 0:
true_states[t] = x_hat
else:
true_states[t] = A @ true_states[t-1] + state_noise[t]
observations[t] = C @ true_states[t] + measurement_noise[t]
# 推定と評価
estimates = np.zeros((n_steps, 2))
for t in range(n_steps):
# **予測ステップ**
x_hat_prior = A @ x_hat
P_prior = A @ P @ A.T + Q
# **更新ステップ**
K = P_prior @ C.T @ np.linalg.inv(C @ P_prior @ C.T + R) # カルマンゲイン
x_hat = x_hat_prior + K @ (observations[t] - C @ x_hat)
P = (np.eye(2) - K @ C) @ P_prior
# 推定値の保存
estimates[t] = x_hat
# 推定誤差の2乗平均値を計算
errors = true_states - estimates
mse = np.mean(np.sum(errors**2, axis=1))
print(f'Mean Squared Error: {mse}')
# 共分散行列とリッカチ方程式の解を表示
P_ss = solve_discrete_are(A, B, Q, R)
print(f'Steady-State Covariance Matrix: {P_ss}')
import numpy as np
import matplotlib.pyplot as plt
# Parameters
k = 1.0 # Spring constant
b = 0.1 # Damping constant
m = 1.0 # Mass
dt = 0.01 # Time step
time = np.arange(0, 10, dt) # Time array
# Initial conditions
theta = np.zeros_like(time) # Angle
omega = np.zeros_like(time) # Angular velocity
torque = np.sin(time) # Input torque (e.g., sine wave)
# Linear model simulation
theta_linear = np.zeros_like(time)
omega_linear = np.zeros_like(time)
for i in range(1, len(time)):
alpha = (torque[i-1] - b * omega_linear[i-1] - k * theta_linear[i-1]) / m
omega_linear[i] = omega_linear[i-1] + alpha * dt
theta_linear[i] = theta_linear[i-1] + omega_linear[i] * dt
# Nonlinear model simulation
theta_nonlinear = np.zeros_like(time)
omega_nonlinear = np.zeros_like(time)
for i in range(1, len(time)):
friction = 0.1 * omega_nonlinear[i-1]**3 # Nonlinear friction
alpha = (torque[i-1] - b * omega_nonlinear[i-1] - k * theta_nonlinear[i-1] - friction) / m
omega_nonlinear[i] = omega_nonlinear[i-1] + alpha * dt
theta_nonlinear[i] = theta_nonlinear[i-1] + omega_nonlinear[i] * dt
# Plotting results
plt.figure(figsize=(14, 6))
# Linear model results
plt.subplot(1, 2, 1)
plt.plot(time, theta_linear, label='Angle')
plt.plot(time, omega_linear, label='Angular Velocity')
plt.title('Linear Model')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
# Nonlinear model results
plt.subplot(1, 2, 2)
plt.plot(time, theta_nonlinear, label='Angle')
plt.plot(time, omega_nonlinear, label='Angular Velocity')
plt.title('Nonlinear Model')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import scipy.linalg
# システム行列
A = np.array([[1, 1],
[0, 1]])
B = np.array([[0.5],
[1.0]])
# コスト行列
Q = np.array([[1, 0],
[0, 1]])
R = np.array([[1]])
# ホライゾン(制御適用期間)
N = 10
# LQRゲインの計算
def dlqr(A, B, Q, R):
# Solve the discrete time LQR controller
X = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
K = np.matrix(scipy.linalg.inv(B.T * X * B + R) * (B.T * X * A))
return np.array(K)
K = dlqr(A, B, Q, R)
# 初期状態
x = np.array([[0],
[1]])
# システムの挙動をシミュレート
states = [x]
for i in range(N):
u = -K @ x
x = A @ x + B @ u
states.append(x)
# ステージコストと蓄積コスト
stage_costs = []
accumulated_cost = 0
for x in states:
stage_cost = x.T @ Q @ x
stage_costs.append(stage_cost.item())
accumulated_cost += stage_cost.item()
# 結果の表示
print("ステージコスト: ", stage_costs)
print("蓄積コスト: ", accumulated_cost)
print("最終状態: \n", states[-1])
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# システム行列
A = np.array([[1, 1],
[0, 1]])
B = np.array([[0.5],
[1.0]])
# コスト行列
Q = np.array([[1, 0],
[0, 1]])
R = np.array([[1]])
# 初期状態
x0 = np.array([[0],
[1]])
# ホライズン(制御適用期間)
N = 10
# 評価関数(総コスト)
def cost_function(u, x0, A, B, Q, R, N):
u = u.reshape((N, -1))
x = x0
total_cost = 0
for k in range(N):
u_k = u[k].reshape((-1, 1))
total_cost += (x.T @ Q @ x + u_k.T @ R @ u_k).item()
x = A @ x + B @ u_k
total_cost += (x.T @ Q @ x).item() # 終端コスト
return total_cost
# 制約条件(終端時刻の状態をゼロにする)
def terminal_constraint(u, x0, A, B, N):
u = u.reshape((N, -1))
x = x0
for k in range(N):
u_k = u[k].reshape((-1, 1))
x = A @ x + B @ u_k
return x.flatten()
# 初期制御入力(ゼロで初期化)
u0 = np.zeros((N * B.shape[1],))
# 制約の定義
constraints = {'type': 'eq', 'fun': lambda u: terminal_constraint(u, x0, A, B, N)}
# 最適化の実行
result = minimize(cost_function, u0, args=(x0, A, B, Q, R, N), constraints=constraints, method='SLSQP')
# 最適制御入力
optimal_u = result.x.reshape((N, -1))
# システムの挙動をシミュレート
x = x0
states = [x]
for u_k in optimal_u:
u_k = u_k.reshape((-1, 1))
x = A @ x + B @ u_k
states.append(x)
# 結果の表示
print("最適制御入力: \n", optimal_u)
print("最終状態: \n", states[-1])
# ステージコストと蓄積コスト
stage_costs = []
accumulated_cost = 0
for k, x in enumerate(states[:-1]):
u_k = optimal_u[k].reshape((-1, 1))
stage_cost = (x.T @ Q @ x + u_k.T @ R @ u_k).item()
stage_costs.append(stage_cost)
accumulated_cost += stage_cost
stage_costs.append((states[-1].T @ Q @ states[-1]).item()) # 終端コスト
accumulated_cost += stage_costs[-1]
print("ステージコスト: ", stage_costs)
print("蓄積コスト: ", accumulated_cost)
# グラフのプロット
time = np.arange(N + 1) # 時間軸(ステップ数)
# 状態のプロット
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(time, [x[0, 0] for x in states], label='x1')
plt.plot(time, [x[1, 0] for x in states], label='x2')
plt.title('State Trajectories')
plt.xlabel('Time Step')
plt.ylabel('State')
plt.legend()
# 制御入力のプロット
plt.subplot(2, 1, 2)
plt.step(time[:-1], [u[0] for u in optimal_u], where='post')
plt.title('Control Inputs')
plt.xlabel('Time Step')
plt.ylabel('Control Input')
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
# 初期状態変数
x0 = np.array([1, 0]) # 例:位置と速度
# システムのパラメータ
A = np.array([[1, 1], [0, 1]]) # 状態遷移行列
B = np.array([[0.5], [1]]) # 入力行列
# 時間ステップ
dt = 1.0
N = 10 # 時間ステップ数
# 評価関数(コスト関数)
def cost(U, x0, A, B, N):
x = x0
total_cost = 0
U = U.reshape(N, 1) # UをN×1の形に変換
for i in range(N):
u = U[i]
total_cost += np.dot(x.T, x) + u**2 # 二次関数
x = np.dot(A, x) + np.dot(B, u)
total_cost += np.dot(x.T, x) # 終端コスト
return total_cost
# 最適化するための制御入力の初期値
U0 = np.zeros(N)
# 最適化の制約(ここでは制約なし)
constraints = []
# 最適化実行
result = minimize(cost, U0, args=(x0, A, B, N), constraints=constraints, method='SLSQP')
# 最適化された制御入力
optimal_U = result.x
# システムの挙動をシミュレート
def simulate_system(x0, A, B, U, N):
x = x0
states = [x]
U = U.reshape(N, 1) # UをN×1の形に変換
for i in range(N):
u = U[i]
x = np.dot(A, x) + np.dot(B, u)
states.append(x)
return np.array(states)
# シミュレーションの実行
states = simulate_system(x0, A, B, optimal_U, N)
# プロット
plt.figure(figsize=(12, 8))
# 制御入力のプロット
plt.subplot(2, 1, 1)
plt.plot(range(N), optimal_U, marker='o')
plt.title('Optimal Control Input')
plt.xlabel('Time Step')
plt.ylabel('Control Input')
# 状態のプロット
plt.subplot(2, 1, 2)
plt.plot(range(N+1), states[:, 0], label='Position')
plt.plot(range(N+1), states[:, 1], label='Velocity')
plt.title('System States')
plt.xlabel('Time Step')
plt.ylabel('State')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
x_min, x_max = -10, 10
t_min, t_max = 0, 2
dx = 0.1
dt = 0.01
x_values = np.arange(x_min, x_max, dx)
t_values = np.arange(t_min, t_max, dt)
# グリッドの初期化
J = np.zeros((len(t_values), len(x_values)))
# 末端条件の設定
J[-1, :] = np.maximum(0, -x_values**2 + 5) # 例: 末端条件
# ハミルトニアンの定義
def hamiltonian(x, p, u):
return 0.5 * (u**2) + p * (x) # システムダイナミクスに合わせて修正
# 最適制御入力の計算
def optimal_control(p):
return -p # ハミルトニアンに合わせて修正
# HJB方程式の数値解法
for t in reversed(range(len(t_values) - 1)):
for i in range(1, len(x_values) - 1):
x = x_values[i]
dJdx = (J[t + 1, i + 1] - J[t + 1, i - 1]) / (2 * dx)
# 最適制御入力の計算
u_star = optimal_control(dJdx)
# ハミルトニアンの評価
H = hamiltonian(x, dJdx, u_star)
# HJB方程式の更新
J[t, i] = J[t + 1, i] + dt * H
# 結果のプロット
X, T = np.meshgrid(x_values, t_values)
plt.contourf(X, T, J, levels=50)
plt.colorbar()
plt.xlabel('x')
plt.ylabel('t')
plt.title('HJB Solution')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import minimize
# ロトカ・ヴォルテラ方程式
def lotka_volterra(y, t, alpha, beta, delta, gamma, u):
X1, X2 = y
dX1dt = alpha * X1 - beta * X1 * X2 + u[0] # 制御入力uを追加
dX2dt = delta * X1 * X2 - gamma * X2 + u[1] # 制御入力uを追加
return [dX1dt, dX2dt]
# コスト関数
def cost_function(U, y0, t, alpha, beta, delta, gamma, Q, R):
U = U.reshape((N, 2))
x = y0
total_cost = 0
for i in range(N):
u = U[i]
x = odeint(lotka_volterra, x, [t[i], t[i + 1]], args=(alpha, beta, delta, gamma, u))[-1]
total_cost += np.dot(x, Q @ x) + np.dot(u, R @ u)
return total_cost
# 制約条件
def control_constraints(U, y0, t, alpha, beta, delta, gamma):
U = U.reshape((N, 2))
x = y0
for i in range(N):
u = U[i]
x = odeint(lotka_volterra, x, [t[i], t[i + 1]], args=(alpha, beta, delta, gamma, u))[-1]
return x - target_state
# パラメータの設定
alpha = 0.1 # 獲物の成長率
beta = 0.02 # 捕食者による獲物の死亡率
delta = 0.01 # 捕食者の繁殖率
gamma = 0.1 # 捕食者の死亡率
# 初期状態と目標状態
X1_0 = 40
X2_0 = 9
y0 = [X1_0, X2_0]
target_state = [20, 5] # 目標状態
# 時間の設定
t = np.linspace(0, 200, 1000)
dt = t[1] - t[0]
N = 10 # ホライズン
# 初期制御入力(ゼロで初期化)
U0 = np.zeros((N, 2))
# コスト行列
Q = np.eye(2)
R = np.eye(2)
# 制約条件
constraints = {'type': 'eq', 'fun': lambda U: control_constraints(U, y0, t[:N + 1], alpha, beta, delta, gamma)}
# 最適化の実行
result = minimize(cost_function, U0.flatten(), args=(y0, t[:N + 1], alpha, beta, delta, gamma, Q, R), constraints=constraints, method='SLSQP')
optimal_U = result.x.reshape((N, 2))
# シミュレーション
x = y0
states = [x]
for u in optimal_U:
x = odeint(lotka_volterra, x, [t[0], t[1]], args=(alpha, beta, delta, gamma, u))[-1]
states.append(x)
states = np.array(states)
# プロット
plt.figure(figsize=(12, 6))
# 獲物の個体数
plt.subplot(2, 1, 1)
plt.plot(t[:N + 1], states[:, 0], label='Prey (X1)')
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Prey Population with MPC Control')
plt.legend()
# 捕食者の個体数
plt.subplot(2, 1, 2)
plt.plot(t[:N + 1], states[:, 1], label='Predator (X2)', color='r')
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Predator Population with MPC Control')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 定数の定義
alpha = 0.01 # 拡散係数
# 空間の設定
x = np.linspace(0, 10, 100)
dx = x[1] - x[0]
# 初期条件
def initial_condition(x):
return np.sin(np.pi * x / 10)
u0 = initial_condition(x)
# 時間の設定
t_span = (0, 1)
t_eval = np.linspace(*t_span, 100)
# 偏微分方程式の定義
def heat_equation(t, u_flat):
u = u_flat.reshape(-1, len(x))
du_dt = np.zeros_like(u)
# 2次元のラプラシアン(拡散項)
du_dt[:, 1:-1] = alpha * (u[:, 2:] - 2 * u[:, 1:-1] + u[:, :-2]) / dx**2
return du_dt.flatten()
# 初期条件の変換
u0_flat = u0.flatten()
# 方程式の解法
sol = solve_ivp(heat_equation, t_span, u0_flat, t_eval=t_eval, method='RK45')
# 結果のプロット
for i, t in enumerate(sol.t):
plt.plot(x, sol.y[:, i], label=f't={t:.2f}')
plt.xlabel('x')
plt.ylabel('u(x,t)')
plt.title('Heat Equation Solution')
plt.legend()
plt.show()
# システムの行列を定義します
A = np.array([[0, 1], [-2, -3]])
B = np.array([[0], [1]])
Q = np.eye(2)
R = np.array([[1]])
# リッカチ方程式を解きます
P = solve_continuous_are(A, B, Q, R)
# 最適レギュレータKを計算します
K = inv(R) @ B.T @ P
print("リッカチ行列 P:")
print(P)
print("最適レギュレータ K:")
print(K)
import numpy as np
from scipy.optimize import approx_fprime
# 非線形システムの定義
def f(x, u):
return np.array([x[0]**2 + x[1]*u, x[1]**2 + u])
# 線形化点
x0 = np.array([1.0, 2.0])
u0 = np.array([0.5])
# ヤコビ行列の計算
def jacobian_f(x, u):
return approx_fprime(x, lambda x: f(x, u), np.sqrt(np.finfo(float).eps))
A = jacobian_f(x0, u0)
print("状態行列 A:")
print(A)
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Objective function
def objective_function(vars):
x, y = vars
return x**2 + y**2 # Example objective function to minimize
# Constraint function
def constraint(vars):
x, y = vars
return x + y - 1 # Example constraint: x + y = 1
# Initial guess
initial_guess = [0.5, 0.5]
# Define the constraint
constraints = {'type': 'eq', 'fun': constraint}
# Perform the optimization
result = minimize(objective_function, initial_guess, constraints=constraints)
# Extract the results
x_opt, y_opt = result.x
objective_value = result.fun
print("Optimal solution:")
print("x =", x_opt)
print("y =", y_opt)
print("Objective function value =", objective_value)
# Create a grid of (x, y) values
x = np.linspace(-0.5, 1.5, 400)
y = np.linspace(-0.5, 1.5, 400)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
# Plotting
plt.figure(figsize=(12, 6))
# Objective function contour plot
plt.contourf(X, Y, Z, levels=50, cmap='viridis', alpha=0.6)
plt.colorbar(label='Objective function value')
# Constraint line
constraint_x = np.linspace(-0.5, 1.5, 400)
constraint_y = 1 - constraint_x
plt.plot(constraint_x, constraint_y, 'r--', label='x + y = 1')
# Optimal point
plt.plot(x_opt, y_opt, 'bo', label='Optimal solution')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Objective Function and Constraint')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# モデルパラメータ
alpha = 0.33 # 生産関数の弾力性
s = 0.2 # 貯蓄率
delta = 0.05 # 減耗率
K0 = 1.0 # 初期資本ストック
# 生産関数
def production_function(K):
return K**alpha
# 状態方程式の定義
def model(K, t):
dKdt = s * production_function(K) - delta * K
return dKdt
# 時間の設定
t = np.linspace(0, 100, 500)
# 状態方程式の解法
K = odeint(model, K0, t)
# プロット
plt.figure(figsize=(12, 6))
plt.plot(t, K, label='Capital Stock K(t)')
plt.xlabel('Time')
plt.ylabel('Capital Stock')
plt.title('Dynamic Behavior of Capital Stock in Solow Growth Model')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# シミュレーションの設定
np.random.seed(0)
T = 100 # 時間ステップ数
t = np.arange(T) # 時間軸
# 仮のデータ生成(例:経済成長率とインフレーション)
true_slope = 0.5
true_intercept = 2.0
X = t.reshape(-1, 1) # 説明変数(時間)
y = true_slope * X.flatten() + true_intercept + np.random.normal(0, 1, T) # 経済指標(データ)
# 線形回帰によるモデルの同定
model = LinearRegression()
model.fit(X, y)
# モデルのパラメータ
estimated_slope = model.coef_[0]
estimated_intercept = model.intercept_
# 将来のデータを生成(例:次の30時間の予測)
future_t = np.arange(T, T + 30).reshape(-1, 1)
future_y = estimated_slope * future_t.flatten() + estimated_intercept
# プロット
plt.figure(figsize=(14, 7))
# 実データと同定結果のプロット
plt.subplot(2, 1, 1)
plt.scatter(t, y, label='Actual Data')
plt.plot(t, model.predict(X), color='r', label='Fitted Line')
plt.xlabel('Time')
plt.ylabel('Economic Indicator')
plt.title('Model Identification')
plt.legend()
plt.grid(True)
# 予測結果のプロット
plt.subplot(2, 1, 2)
plt.plot(np.concatenate([t, future_t.flatten()]),
np.concatenate([model.predict(X), future_y]),
color='b', label='Predicted')
plt.axvline(x=T, color='g', linestyle='--', label='Prediction Start')
plt.xlabel('Time')
plt.ylabel('Economic Indicator')
plt.title('Forecast')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt
# ロジスティック成長モデルの微分方程式
def logistic_growth(P, t, r):
K = 1000 # 環境の収容能力
dP_dt = r * P * (1 - P / K)
return dP_dt
# 目的関数
def objective(params):
r = params[0] # 成長率
P0 = 10 # 初期個体数
P_target = 500 # 目標個体数
T = 100 # シミュレーションの時間
t = np.linspace(0, T, 100)
# 微分方程式の解
P = odeint(logistic_growth, P0, t, args=(r,))
# 目的関数の計算 (個体数と目標個体数の差の平方和)
cost = np.sum((P - P_target) ** 2)
return cost
# 初期推定
initial_guess = [0.1]
# 最適化
result = minimize(objective, initial_guess, bounds=[(0, None)])
# 結果の表示
optimal_r = result.x[0]
print(f"Optimal growth rate: {optimal_r}")
# 最適な成長率でシミュレーション
P0 = 10
T = 100
t = np.linspace(0, T, 100)
P_optimal = odeint(logistic_growth, P0, t, args=(optimal_r,))
# 結果のプロット
plt.plot(t, P_optimal, label=f'Optimal Growth Rate (r={optimal_r:.2f})')
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Bacterial Growth with Optimal Control')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_continuous_are
from scipy.linalg import inv
# システムのパラメータ
k1 = 1.0 # 反応速度定数
A = np.array([[-k1, 0], [k1, 0]]) # 状態遷移行列
B = np.array([[1], [0]]) # 制御行列
Q = np.eye(2) # 状態重み行列
R = np.array([[1]]) # 制御重み行列
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 最適制御ゲインを計算
K = inv(R) @ B.T @ P
# シミュレーションのパラメータ
T = 10
dt = 0.1
t = np.arange(0, T, dt)
x0 = np.array([10, 0]) # 初期状態
x = np.zeros((len(t), 2))
x[0, :] = x0
# システムのシミュレーション
for i in range(1, len(t)):
u = -K @ x[i-1, :] # 最適制御入力
x[i, :] = x[i-1, :] + (A @ x[i-1, :] + B.flatten() * u) * dt
# 結果のプロット
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(t, x[:, 0], label='Substrate (S)')
plt.xlabel('Time')
plt.ylabel('Concentration')
plt.title('Substrate Concentration Over Time')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
plt.plot(t, x[:, 1], label='Product (P)', color='orange')
plt.xlabel('Time')
plt.ylabel('Concentration')
plt.title('Product Concentration Over Time')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_continuous_are, inv
# モデルのパラメータ
alpha = np.array([0.1, 0.05, 0.2]) # 状態遷移の減衰係数
beta = np.array([1, 1, 1]) # 制御入力の影響
# 状態遷移行列Aと制御行列Bの設定
A = np.diag(-alpha)
B = np.reshape(beta, (3, 1))
Q = np.eye(3) # 状態重み行列
R = np.array([[1]]) # 制御重み行列
# リカッチ方程式を解いてPを計算
P = solve_continuous_are(A, B, Q, R)
# 状態フィードバックゲインKの計算
K = inv(R) @ B.T @ P
print("最適状態フィードバックゲイン K:")
print(K)
# シミュレーションのパラメータ
T = 20
dt = 0.1
t = np.arange(0, T, dt)
x0 = np.array([10, 7, 5]) # 初期状態(温度、pH、栄養素濃度)
x = np.zeros((len(t), 3))
x[0, :] = x0
# システムのシミュレーション
for i in range(1, len(t)):
u = -K @ x[i-1, :] # 状態フィードバック制御入力
x[i, :] = x[i-1, :] + (A @ x[i-1, :] + B.flatten() * u) * dt
# 結果のプロット
plt.figure(figsize=(12, 6))
plt.subplot(1, 3, 1)
plt.plot(t, x[:, 0], label='Temperature (T)')
plt.xlabel('Time')
plt.ylabel('Temperature')
plt.title('Temperature Over Time')
plt.legend()
plt.grid(True)
plt.subplot(1, 3, 2)
plt.plot(t, x[:, 1], label='pH (pH)', color='orange')
plt.xlabel('Time')
plt.ylabel('pH')
plt.title('pH Over Time')
plt.legend()
plt.grid(True)
plt.subplot(1, 3, 3)
plt.plot(t, x[:, 2], label='Nutrients (N)', color='green')
plt.xlabel('Time')
plt.ylabel('Nutrients')
plt.title('Nutrients Over Time')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# 擬似的な地震データの生成(例としてランダムデータを使用)
np.random.seed(42)
time = np.arange(0, 100, 1)
earthquake_activity = np.sin(time / 5) + np.random.normal(0, 0.2, len(time)) # ノイズを少なく
# カルマンフィルタのパラメータ設定
n = len(time)
A = 1 # 状態遷移行列
B = 0 # 制御入力行列(今回は制御なし)
H = 1 # 観測行列
Q = 1e-5 # プロセスノイズの共分散(小さく設定)
R = 0.2**2 # 観測ノイズの共分散(小さく設定)
# 初期化
x_hat = np.zeros(n) # 推定値
P = np.zeros(n) # 推定誤差共分散
x_hat[0] = earthquake_activity[0] # 初期推定値
P[0] = 1 # 初期誤差共分散
# カルマンフィルタの適用
for k in range(1, n):
# 予測ステップ
x_hat[k] = A * x_hat[k-1] + B
P[k] = A * P[k-1] * A + Q
# 更新ステップ
K = P[k] * H / (H * P[k] * H + R)
x_hat[k] = x_hat[k] + K * (earthquake_activity[k] - H * x_hat[k])
P[k] = (1 - K * H) * P[k]
# 結果のプロット
plt.figure(figsize=(12, 6))
plt.plot(time, earthquake_activity, label='Actual Earthquake Activity', color='blue')
plt.plot(time, x_hat, label='Filtered Earthquake Activity', color='red', linestyle='--')
plt.xlabel('Time')
plt.ylabel('Earthquake Activity')
plt.title('Earthquake Activity Prediction with Improved Kalman Filter')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# システムのパラメータ
Kp = 2.0 # 比例ゲイン
Ki = 0.5 # 積分ゲイン
Kd = 0.1 # 微分ゲイン
# PID制御の計算
def pid_control(setpoint, measurement, integral, previous_error, dt):
error = setpoint - measurement
integral += error * dt
derivative = (error - previous_error) / dt
control_signal = Kp * error + Ki * integral + Kd * derivative
return control_signal, integral, error
# システムモデルの定義
def system_model(y, t, control_signal):
dydt = -0.1 * y + control_signal
return dydt
# シミュレーションのパラメータ
T = 20
dt = 0.1
time = np.arange(0, T, dt)
setpoint = 10
measurement = 0
integral = 0
previous_error = 0
# 結果の保存
y = np.zeros_like(time)
for i in range(len(time)):
control_signal, integral, previous_error = pid_control(setpoint, measurement, integral, previous_error, dt)
y[i] = odeint(system_model, measurement, [0, dt], args=(control_signal,))[1]
measurement = y[i]
# 結果のプロット
plt.plot(time, y, label='Measured Value')
plt.axhline(y=setpoint, color='r', linestyle='--', label='Setpoint')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('PID Control for Cell Cultivation')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
from scipy.linalg import solve_continuous_are, inv
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 状態空間モデルのパラメータ
alpha = 0.1 # 発現量の減衰率
beta = 1.0 # 制御入力の影響
# 状態行列 A と入力行列 B の定義
A = np.array([[-alpha]])
B = np.array([[beta]])
# コスト行列 Q と R の設定
Q = np.array([[1]]) # 発現量のコスト
R = np.array([[1]]) # 制御入力のコスト
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 最適フィードバックゲイン K の計算
K = inv(R) @ B.T @ P
print("最適制御ゲイン K:")
print(K)
# 微分方程式の定義
def gene_expression(t, x):
u = -K @ x # 最適フィードバック制御
dxdt = A @ x + B @ u
return dxdt
# 初期条件
x0 = [1.0] # 初期発現量
# 時間範囲
t_span = (0, 50) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(gene_expression, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.plot(sol.t, sol.y[0], label='Gene Expression with LQR Control')
plt.xlabel('Time')
plt.ylabel('Gene Expression')
plt.title('Gene Expression Dynamics with Optimal Control')
plt.legend()
plt.grid()
plt.show()
import numpy as np
from scipy.linalg import solve_continuous_are, inv
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# 2次反応の速度定数
k = 0.1
# 状態空間モデルの定義
def state_space_model(t, x):
x1, x2 = x
dx1_dt = x2
dx2_dt = -k * x1**2
return [dx1_dt, dx2_dt]
# 状態空間モデルのパラメータ
A = np.array([[0, 1], [0, 0]])
B = np.array([[0], [0]])
# コスト行列 Q と R の設定
Q = np.array([[10, 0], [0, 1]]) # 状態コスト行列(濃度とその微分のコスト)
R = np.array([[1]]) # 入力コスト行列(ここでは入力がないため0)
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 最適フィードバックゲイン K の計算
K = inv(R) @ B.T @ P
print("最適制御ゲイン K:")
print(K)
# 微分方程式の定義(LQR制御を含む)
def controlled_reactor(t, x):
u = -K @ x # 最適フィードバック制御
dx1_dt = x[1]
dx2_dt = -k * x[0]**2
return [dx1_dt, dx2_dt]
# 初期条件
x0 = [1.0, 0.0] # 初期濃度とその微分
# 時間範囲
t_span = (0, 50) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(controlled_reactor, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.plot(sol.t, sol.y[0], label='Concentration of A with LQR Control')
plt.xlabel('Time')
plt.ylabel('Concentration')
plt.title('Concentration of A in Second-Order Reaction with Optimal Control')
plt.legend()
plt.grid()
plt.show()
import numpy as np
from scipy.linalg import solve_continuous_are, inv
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from scipy.signal import place_poles
# 捕食モデルのパラメータ
alpha = 0.1 # 被捕食者の成長率
beta = 0.02 # 捕食率
delta = 0.01 # 捕食者の成長率
gamma = 0.1 # 捕食者の死亡率
# 状態空間モデルの定義
A = np.array([[alpha, -beta],
[delta, -gamma]])
B = np.array([[0],
[0]])
# コスト行列 Q と R の設定
Q = np.diag([10, 10]) # 状態コスト行列
R = np.array([[1]]) # 入力コスト行列(ここでは入力がないため0)
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 最適フィードバックゲイン K の計算
K = inv(R) @ B.T @ P
print("最適制御ゲイン K:")
print(K)
# 微分方程式の定義(LQR制御を含む)
def predator_prey_lqr(t, z):
u = -K @ z # 最適フィードバック制御
dx1_dt = alpha * z[0] - beta * z[0] * z[1] + u[0]
dx2_dt = delta * z[0] * z[1] - gamma * z[1] + u[1]
return [dx1_dt, dx2_dt]
# 初期条件
x0 = [40, 9] # 初期の被捕食者と捕食者の個体数
# 時間範囲
t_span = (0, 200) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(predator_prey_lqr, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.figure(figsize=(12, 6))
# 被捕食者と捕食者の個体数のプロット
plt.subplot(1, 2, 1)
plt.plot(sol.t, sol.y[0], label='Prey (X)')
plt.plot(sol.t, sol.y[1], label='Predator (Y)')
plt.xlabel('Time')
plt.ylabel('Population')
plt.title('Predator-Prey Dynamics with LQR Control')
plt.legend()
plt.grid()
# フェーズ平面のプロット
plt.subplot(1, 2, 2)
plt.plot(sol.y[0], sol.y[1])
plt.xlabel('Prey (X)')
plt.ylabel('Predator (Y)')
plt.title('Phase Plane with LQR Control')
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# 細胞培養の温度モデルのパラメータ
k1 = 0.1 # 細胞の成長率(温度に依存)
k2 = 0.05 # 温度の変化率
T_setpoint = 37 # 目標温度(摂氏)
# 状態空間モデルの定義
def cell_culture(t, z, u):
T, C = z
dT_dt = k2 * (u - T) # 温度の変化
dC_dt = k1 * (T - T_setpoint) * C # 細胞の成長
return [dT_dt, dC_dt]
# コントローラー(PI制御)
def control_law(T, T_setpoint):
Kp = 1.0 # 比例ゲイン
Ki = 0.1 # 積分ゲイン
integral = 0 # 積分項
error = T_setpoint - T
integral += error
u = Kp * error + Ki * integral
return u, integral
# 初期条件
T0 = 25 # 初期温度
C0 = 1 # 初期細胞濃度
x0 = [T0, C0] # 初期状態
# 時間範囲
t_span = (0, 50) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 制御ループの定義
def temperature_control(t, z):
T, C = z
u, integral = control_law(T, T_setpoint)
return cell_culture(t, z, u)
# 微分方程式の解法
sol = solve_ivp(temperature_control, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.figure(figsize=(12, 6))
# 温度と細胞濃度のプロット
plt.subplot(1, 2, 1)
plt.plot(sol.t, sol.y[0], label='Temperature (T)')
plt.plot(sol.t, sol.y[1], label='Cell Concentration (C)')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Cell Culture with Temperature Control')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.linalg import solve_continuous_are, inv
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# 発酵プロセスのパラメータ
k1 = 0.1 # 基質の減少率
k2 = 0.01 # 基質と生成物の反応率
k3 = 0.01 # 基質から生成物の生成率
k4 = 0.1 # 生成物の減少率
# 状態空間モデルの定義
A = np.array([[-k1, -k2],
[k3, -k4]])
B = np.array([[1],
[0]])
# コスト行列 Q と R の設定
Q = np.diag([10, 10]) # 状態コスト行列
R = np.array([[1]]) # 入力コスト行列
# リカッチ方程式を解く
P = solve_continuous_are(A, B, Q, R)
# 最適フィードバックゲイン K の計算
K = inv(R) @ B.T @ P
print("最適制御ゲイン K:")
print(K)
# 微分方程式の定義(LQR制御を含む)
def fermentation_process_lqr(t, z):
u = -K @ z # 最適フィードバック制御
dx1_dt = -k1 * z[0] - k2 * z[0] * z[1] + u[0]
dx2_dt = k3 * z[0] * z[1] - k4 * z[1]
return [dx1_dt, dx2_dt]
# 初期条件
x0 = [10, 5] # 初期の基質と生成物の濃度
# 時間範囲
t_span = (0, 100) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(fermentation_process_lqr, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.figure(figsize=(12, 6))
# 基質と生成物の濃度のプロット
plt.subplot(1, 2, 1)
plt.plot(sol.t, sol.y[0], label='Substrate (X1)')
plt.plot(sol.t, sol.y[1], label='Product (X2)')
plt.xlabel('Time')
plt.ylabel('Concentration')
plt.title('Fermentation Process with LQR Control')
plt.legend()
plt.grid()
# フェーズ平面のプロット
plt.subplot(1, 2, 2)
plt.plot(sol.y[0], sol.y[1])
plt.xlabel('Substrate (X1)')
plt.ylabel('Product (X2)')
plt.title('Phase Plane with LQR Control')
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# 蒸気機関のパラメータ
k1 = 0.1 # 回転速度の減衰係数
k2 = 0.5 # 燃料供給の効率
# 状態空間モデルの定義
def steam_engine(t, z):
theta, omega = z
# フィードバック制御:目標回転速度に基づく制御入力
theta_setpoint = 10 # 目標回転角度
u = k2 * (theta_setpoint - theta)
dtheta_dt = omega
domega_dt = -k1 * omega + u
return [dtheta_dt, domega_dt]
# 初期条件
theta0 = 0 # 初期回転角度
omega0 = 0 # 初期回転速度
x0 = [theta0, omega0]
# 時間範囲
t_span = (0, 50) # シミュレーションの時間範囲
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(steam_engine, t_span, x0, t_eval=t_eval)
# 結果のプロット
plt.figure(figsize=(12, 6))
# 回転角度と回転速度のプロット
plt.subplot(1, 2, 1)
plt.plot(sol.t, sol.y[0], label='Angle (θ)')
plt.plot(sol.t, sol.y[1], label='Speed (ω)')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Steam Engine Dynamics')
plt.legend()
plt.grid()
# フェーズ平面のプロット
plt.subplot(1, 2, 2)
plt.plot(sol.y[0], sol.y[1])
plt.xlabel('Angle (θ)')
plt.ylabel('Speed (ω)')
plt.title('Phase Plane')
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 反応器のパラメータ
k = 0.1 # 反応速度定数
V = 1.0 # 反応器の体積(L)
rho = 1.0 # 反応液の密度(kg/L)
cp = 4.18 # 比熱(J/kg·K)
U = 0.5 # 熱伝達係数(W/K)
# 制御パラメータ
Kp = 5.0 # 比例ゲイン
Ki = 1.0 # 積分ゲイン
# 温度制御の状態空間モデルの定義
def reactor_temperature(t, z):
T, T_setpoint, integral = z
error = T_setpoint - T
control = Kp * error + Ki * integral
dT_dt = (control - U * (T - 20.0)) / (rho * cp * V) # 温度変化の計算
integral_dt = error * dt # 積分の計算
return [dT_dt, 0, integral_dt]
# 初期条件
T0 = 20.0 # 初期温度(℃)
T_setpoint = 50.0 # 設定温度(℃)
integral0 = 0.0
z0 = [T0, T_setpoint, integral0]
# 時間範囲
dt = 0.1 # 時間の刻み幅
t_span = (0, 100) # シミュレーションの時間範囲
t_eval = np.arange(t_span[0], t_span[1], dt) # 評価する時間点
# 微分方程式の解法
sol = solve_ivp(reactor_temperature, t_span, z0, t_eval=t_eval)
# 結果のプロット
plt.figure(figsize=(12, 6))
# 温度のプロット
plt.plot(sol.t, sol.y[0], label='Reactor Temperature (T)')
plt.axhline(y=T_setpoint, color='r', linestyle='--', label='Setpoint (T_setpoint)')
plt.xlabel('Time (s)')
plt.ylabel('Temperature (°C)')
plt.title('Reactor Temperature Control')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# ミカエリス-メンテン方程式の反応速度関数
def michaelis_menten(S, V_max, K_m):
return V_max * S / (K_m + S)
# システムのダイナミクス
def system_dynamics(S, u, V_max, K_m):
v = michaelis_menten(S, V_max, K_m)
dSdt = -v + u
return dSdt
# コスト関数の定義
def cost_function(control_input, t, S0, V_max, K_m):
# 制御入力を時間に合わせて定義
control_input_interp = np.interp(t, np.linspace(0, t[-1], len(control_input)), control_input)
# 状態の初期条件
S = S0
S_values = []
dt = t[1] - t[0] # 時間刻み
for ti in t:
u = np.interp(ti, t, control_input_interp)
S += system_dynamics(S, u, V_max, K_m) * dt
S_values.append(S)
# コストを計算(例: 基質濃度と制御入力の二乗和)
S_values = np.array(S_values)
return np.sum(S_values**2 + control_input_interp**2)
# パラメータ設定
V_max = 1.0 # 最大反応速度
K_m = 0.5 # ミカエリス定数
S0 = 1.0 # 初期基質濃度
t = np.linspace(0, 10, 50) # 時間の範囲(0から10まで、50点)
initial_control_input = np.zeros_like(t) # 初期制御入力(ゼロ)
# 制御入力を最適化
result = minimize(cost_function, initial_control_input, args=(t, S0, V_max, K_m), method='BFGS')
# 最適制御入力と状態のプロット
optimal_control_input = result.x
control_input_interp = np.interp(t, np.linspace(0, t[-1], len(optimal_control_input)), optimal_control_input)
S_values = []
S = S0
dt = t[1] - t[0] # 時間刻み
for ti in t:
u = np.interp(ti, t, control_input_interp)
S += system_dynamics(S, u, V_max, K_m) * dt
S_values.append(S)
S_values = np.array(S_values)
plt.figure(figsize=(12, 6))
# プロット: 最適制御入力
plt.subplot(2, 1, 1)
plt.plot(t, control_input_interp, label='Optimal Control Input')
plt.xlabel('Time')
plt.ylabel('Control Input')
plt.title('Optimal Control Input Over Time')
plt.legend()
# プロット: 基質濃度の変化
plt.subplot(2, 1, 2)
plt.plot(t, S_values, label='Substrate Concentration')
plt.xlabel('Time')
plt.ylabel('Substrate Concentration')
plt.title('Substrate Concentration Over Time')
plt.legend()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# ナビエ-ストークス方程式のシミュレーションデータを生成(ここではダミーデータを使用)
def generate_data(nx, ny):
X = []
y = []
for i in range(nx):
for j in range(ny):
state = np.array([i, j])
u = np.sin(state[0] + state[1]) # ダミーの制御入力
X.append(state)
y.append(u)
return np.array(X), np.array(y)
# データ生成
nx, ny = 5, 5
X, y = generate_data(nx, ny)
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 線形回帰モデルの訓練
model = LinearRegression()
model.fit(X_train, y_train)
# モデルの評価
y_pred = model.predict(X_test)
plt.scatter(y_test, y_pred)
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.title('Linear Regression Predictions vs True Values')
plt.show()
# 予測の例
sample_state = np.array([[2, 2]])
predicted_u = model.predict(sample_state)
print(f'Predicted control input for state {sample_state}: {predicted_u}')
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_bvp
from scipy.linalg import solve_continuous_are, inv
# 定数の定義
E = 210e9 # ヤング率 (Pa)
I = 1e-6 # 断面二次モーメント (m^4)
L = 10.0 # 梁の長さ (m)
q = 1000 # 一様荷重 (N/m)
n = 100 # 数値解の分割数
# 微分方程式の定義
def beam_eq(x, y):
dydx = np.zeros_like(y)
dydx[0] = y[1]
dydx[1] = q / (E * I)
return dydx
# 境界条件の定義
def boundary_conditions(ya, yb):
return np.array([ya[0], yb[1]])
# 数値解の計算
x = np.linspace(0, L, n)
y_initial = np.zeros((2, x.size))
# 境界条件: w(0) = 0, w'(L) = 0
solution = solve_bvp(beam_eq, boundary_conditions, x, y_initial)
# LQR制御の設定
def create_state_space_matrices(E, I, L, h):
m = int(L / h) + 1
A = np.zeros((2*m, 2*m))
B = np.zeros((2*m, m))
for i in range(m):
A[i, i+m] = 1
if i < m-1:
A[i+m, i] = -2*E*I / h**4
A[i+m, i+1] = 4*E*I / h**4
A[i+m, i+2] = -6*E*I / h**4
A[i+m, i+3] = 4*E*I / h**4
A[i+m, i+4] = -E*I / h**4
for i in range(m):
B[i+m, i] = 1 / (E*I)
C = np.eye(2*m)
D = np.zeros((2*m, m))
return A, B, C, D
def lqr_control(A, B, Q, R):
P = solve_continuous_are(A, B, Q, R)
K = inv(R) @ B.T @ P
return K
# LQR制御器の設計
h = L / n
A, B, C, D = create_state_space_matrices(E, I, L, h)
Q = np.eye(A.shape[0])
R = np.eye(B.shape[1])
K = lqr_control(A, B, Q, R)
# 初期状態
x0 = np.zeros(A.shape[0])
# 状態のシミュレーション
def simulate_system(A, B, K, x0, num_steps, dt):
states = np.zeros((num_steps, A.shape[0]))
x = x0.copy()
for i in range(num_steps):
u = -K @ x
x = A @ x + B @ u
states[i] = x
return states
num_steps = 100
dt = 0.1
states = simulate_system(A, B, K, x0, num_steps, dt)
# 結果のプロット
plt.figure(figsize=(12, 6))
plt.plot(solution.x, solution.y[0], label='Displacement (w)')
plt.xlabel('Position along the beam (m)')
plt.ylabel('Displacement (m)')
plt.title('Displacement of a Beam under Uniform Load')
plt.legend()
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eigh
from sklearn.cluster import KMeans
# システムパラメータ
n = 10 # モード数
L = 1.0 # 梁の長さ
h = L / (n - 1) # グリッドの間隔
# 剛性行列と質量行列の作成
K = np.zeros((n, n))
M = np.zeros((n, n))
for i in range(n):
for j in range(n):
if i == j:
K[i, j] = 2 / h**2
M[i, j] = h / 6
elif abs(i - j) == 1:
K[i, j] = -1 / h**2
M[i, j] = h / 12
# 固有値問題の解法
eigenvalues, eigenvectors = eigh(K, M)
# 自然周波数の計算
natural_frequencies = np.sqrt(eigenvalues)
# K-meansクラスタリングの実行
num_clusters = 3 # クラスタ数
kmeans = KMeans(n_clusters=num_clusters)
kmeans.fit(eigenvectors)
labels = kmeans.labels_
# モード形状のプロット
plt.figure(figsize=(12, 6))
x = np.linspace(0, L, n)
for i in range(3): # 最初の3つのモードをプロット
plt.plot(x, eigenvectors[:, i], label=f'Mode {i+1} (Frequency = {natural_frequencies[i]:.2f} Hz)')
plt.xlabel('Position along the beam (m)')
plt.ylabel('Mode shape')
plt.title('Vibration Modes of a Beam')
plt.legend()
plt.grid()
plt.show()
# クラスタリング結果のプロット
plt.figure(figsize=(10, 6))
plt.scatter(range(n), eigenvectors[:, 0], c=labels, cmap='viridis')
plt.colorbar(label='Cluster')
plt.xlabel('Mode index')
plt.ylabel('Mode shape component')
plt.title('Clustering of Mode Shapes')
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# システムパラメータ
L = 1.0 # 長さ
Nx = 10 # 空間的分割数
dx = L / (Nx - 1)
alpha = 0.01 # 熱拡散率
dt = 0.01 # 時間刻み
T_end = 2.0 # シミュレーション終了時間
Nx = 10
nt = int(T_end / dt) # 時間ステップ数
target_temperature = 1.0 # 目標温度
# 初期条件
u0 = np.zeros(Nx)
u0[0] = 1.0 # 初期の温度分布
def heat_eq(t, u):
# u: 温度のベクトル
u = np.reshape(u, (Nx,))
du = np.zeros(Nx)
du[1:-1] = alpha * (u[2:] - 2 * u[1:-1] + u[:-2]) / dx**2
du[0] = 0 # 境界条件(左端)
du[-1] = 0 # 境界条件(右端)
return du
# 温度の時間発展
sol = solve_ivp(heat_eq, [0, T_end], u0, t_eval=np.arange(0, T_end, dt))
# 結果のプロット
plt.figure(figsize=(10, 6))
for i in range(0, nt, nt // 5): # いくつかのタイムステップでプロット
plt.plot(np.linspace(0, L, Nx), sol.y[:, i], label=f'Time = {sol.t[i]:.2f} s')
plt.xlabel('Position along the beam (m)')
plt.ylabel('Temperature')
plt.title('Temperature Distribution Over Time')
plt.legend()
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_model import ARIMA
# 定数
c = 3.0e8 # 光速 (m/s)
dx = 1.0e-3 # 空間の離散化間隔 (m)
dt = dx / (2 * c) # 時間の離散化間隔 (s)
# シミュレーション領域のサイズ
nx = 200
nt = 200
x = np.linspace(0, (nx-1)*dx, nx)
t = np.linspace(0, (nt-1)*dt, nt)
# 電場と磁場の初期化
E = np.zeros((nx, nt))
H = np.zeros((nx, nt))
# 初期条件 (脈冲)
E[int(nx/4), 0] = 1.0
# シミュレーションループ
for n in range(0, nt-1):
for i in range(1, nx-1):
H[i, n+1] = H[i, n] - (dt / (dx * 4 * np.pi * 1e-7)) * (E[i+1, n] - E[i, n])
E[i, n+1] = E[i, n] - (dt / (dx * 8.854e-12)) * (H[i, n+1] - H[i-1, n+1])
# 電場の時系列データの抽出
E_series = E[int(nx/4), :] # 例として、位置 x = int(nx/4) での電場データ
# ARIMAモデルの適用
model = ARIMA(E_series, order=(5, 1, 0)) # (p, d, q) のパラメータは調整可能
model_fit = model.fit(disp=0)
# 予測
forecast_steps = 50 # 予測するステップ数
forecast, stderr, conf_int = model_fit.forecast(steps=forecast_steps)
# 予測結果のプロット
plt.figure(figsize=(12, 6))
plt.plot(t, E_series, label='Observed')
plt.plot(t[-1] + dt*np.arange(1, forecast_steps+1), forecast, label='Forecast', color='red')
plt.fill_between(t[-1] + dt*np.arange(1, forecast_steps+1),
forecast - 1.96*stderr,
forecast + 1.96*stderr,
color='red', alpha=0.3)
plt.xlabel('Time (s)')
plt.ylabel('Electric Field (V/m)')
plt.title('Electric Field Forecast')
plt.legend()
plt.show()
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import IsolationForest
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
# データの生成(ここでは仮の振動データを使用)
np.random.seed(0)
normal_data = np.random.normal(0, 1, (1000, 2)) # 正常な振動データ
anomaly_data = np.random.normal(10, 1, (50, 2)) # 異常な振動データ
data = np.vstack((normal_data, anomaly_data))
labels = np.array([0] * 1000 + [1] * 50) # 0:正常, 1:異常
# データフレームの作成
df = pd.DataFrame(data, columns=['Feature1', 'Feature2'])
df['Label'] = labels
# データの前処理
X = df[['Feature1', 'Feature2']]
y = df['Label']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# データの標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Isolation Forest モデルの訓練
model = IsolationForest(contamination=0.05, random_state=0)
model.fit(X_train_scaled)
# 異常の予測
y_pred = model.predict(X_test_scaled)
y_pred = np.where(y_pred == -1, 1, 0) # -1が異常、1が正常
# 結果の可視化
plt.figure(figsize=(10, 6))
plt.scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], c=y_pred, cmap='coolwarm', marker='o')
plt.title('Anomaly Detection Results')
plt.xlabel('Feature1')
plt.ylabel('Feature2')
plt.colorbar(label='Anomaly')
plt.show()
# 精度の評価
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
import numpy as np
from sklearn.linear_model import LinearRegression
from scipy.optimize import minimize
import matplotlib.pyplot as plt
# システムのダイナミクスモデル(線形回帰モデル)
class LinearSystemModel:
def __init__(self):
self.model = LinearRegression()
def fit(self, X, y):
self.model.fit(X, y)
def predict(self, X):
return self.model.predict(X)
# MPCのパラメータ
N = 10 # 予測ホライズン
Q = 1 # 状態の重み
R = 1 # 入力の重み
# 最適化関数
def mpc_cost(u, x0, system_model, N, Q, R):
x = x0
cost = 0
for i in range(N):
x_next = system_model.predict(np.array([x]))[0]
cost += Q * np.sum(x_next**2) + R * u[i]**2
x = x_next + u[i]
return cost
# システムのシミュレーション
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 1)
y = 2 * X + np.random.normal(0, 0.1, size=(n_samples, 1))
system_model = LinearSystemModel()
system_model.fit(X, y)
# MPCの設定
x0 = np.array([0]) # 初期状態
u0 = np.zeros(N) # 初期入力
bounds = [(-1, 1)] * N # 入力の制約
# 最適化
result = minimize(mpc_cost, u0, args=(x0, system_model, N, Q, R), bounds=bounds)
optimal_u = result.x
# 結果の表示
print("Optimal control inputs:", optimal_u)
# システムの応答をプロット
x = x0
response = [x]
for u in optimal_u:
x_next = system_model.predict(np.array([x]))[0]
response.append(x_next + u)
x = x_next + u
plt.plot(response, label='System Response')
plt.xlabel('Time step')
plt.ylabel('State')
plt.title('System Response with Optimal Control Inputs')
plt.legend()
plt.show()
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
# データの生成
Vgs = np.linspace(0, 5, 100).reshape(-1, 1) # ゲート電圧 (入力データ)
Id = np.where(Vgs > Vth, k * (Vgs - Vth)**2, 0).reshape(-1, 1) # ドレイン電流 (出力データ)
# 多項式特徴量の作成
poly = PolynomialFeatures(degree=2)
Vgs_poly = poly.fit_transform(Vgs)
# 線形回帰モデルの学習
model = LinearRegression()
model.fit(Vgs_poly, Id)
# 予測の計算
Id_pred = model.predict(Vgs_poly)
# プロットの作成
plt.figure(figsize=(8, 6))
plt.scatter(Vgs, Id, color='b', label='Actual Data')
plt.plot(Vgs, Id_pred, color='r', linestyle='--', label='Fitted Curve')
plt.title('MOSFET Characteristic Curve with Machine Learning Fit')
plt.xlabel('Gate-Source Voltage Vgs (V)')
plt.ylabel('Drain Current Id (A)')
plt.grid(True)
plt.legend()
plt.show()
# モデルの評価
mse = mean_squared_error(Id, Id_pred)
print(f"Mean Squared Error: {mse:.4f}")
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定と初期化
tm = 5000 # シミュレーション時間
ie = 0 # 誤差積分値初期値
# PID制御器の定義
def PID(err, prerr):
global ie
kp = 1 # 比例ゲイン
ki = 0 # 積分ゲイン
kd = 100 # 微分ゲイン
ie = err + ie
Δerr = err - prerr
return kp * err + ki * ie + kd * Δerr
# 目標値の設定
def setpoint(simtime):
return 100
# プラントモデルの定義
def Plant(y, x, input, simtime):
u_max = 10 # 非捕食者の最大投入数
u_min = -10 # 非捕食者の最大屠殺数
u = max(min(input, u_max), u_min)
print(u)
Δx = ((1 - 0.01 * y) * x + u) * 0.01
Δy = ((-1 + 0.02 * x) * y) * 0.01
hosyoku = y + Δy
hihosyoku = x + Δx
if y + Δy < 0:
hosyoku = 0
if x + Δx < 0:
hihosyoku = 0
return hosyoku, hihosyoku
# シミュレーションの実行
u = np.zeros(tm + 1)
x = np.zeros(tm + 1) # 非捕食者の個体数
y = np.zeros(tm + 1) # 捕食者の個体数
r = np.zeros(tm + 1)
er = np.zeros(tm + 1)
y[0] = 20 # 捕食者の初期値
x[0] = 20 # 非捕食者の初期値
for t in range(tm):
prer = r[t] - y[t]
y[t + 1], x[t + 1] = Plant(y[t], x[t], u[t], t)
r[t + 1] = setpoint(t)
er[t + 1] = r[t + 1] - y[t + 1]
u[t + 1] = PID(er[t + 1], prer)
# プロット
plt.figure(figsize=(10, 6))
plt.plot(range(tm + 1), y, label='y (Predators)')
plt.plot(range(tm + 1), x, label='x (Prey)')
plt.plot(range(tm + 1), r, label='Setpoint')
plt.xlabel('Time')
plt.ylabel('Population')
plt.legend()
plt.grid(True)
# x軸とy軸の表示範囲を指定
plt.xlim(0, tm) # x軸の範囲を設定
plt.ylim(0, max(max(y), max(x), max(r)) * 1.1) # y軸の範囲を設定
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定と初期化
tm = 50 # シミュレーション時間
ie = 0 # 誤差積分値初期値
beta = 1 # βの値
# PID制御器の定義
def PID(err, prerr):
global ie
kp = 0.01 # 比例ゲイン
Ti = 1 # 積分時間
Td = 0 # 微分時間
ki = kp / Ti # 積分ゲイン
kd = kp * Td # 微分ゲイン
ie = err + ie
Δerr = err - prerr
return kp * err + ki * ie + kd * Δerr
# 目標値の設定
def setpoint(simtime):
return 50
# プラントモデルの定義
def Plant(ypre, input, simtime):
food_max = 100 # エサの量最大値
food_min = 0.001 # エサの量最小値
u = max(min(input, food_max), food_min)
Δw = u * ypre**(2/3) - beta * ypre
case = [u, Δw]
print(case)
return ypre + Δw
# シミュレーションの実行
u = np.zeros(tm + 1)
y = np.zeros(tm + 1)
r = np.zeros(tm + 1)
er = np.zeros(tm + 1)
y[0] = 10 # 体重初期値
for t in range(tm):
prer = r[t] - y[t]
y[t + 1] = Plant(y[t], u[t], t)
r[t + 1] = setpoint(t)
er[t + 1] = r[t + 1] - y[t + 1]
u[t + 1] = PID(er[t + 1], prer)
# プロット
plt.figure(figsize=(10, 6))
plt.plot(range(tm + 1), y, label='y (Weight)')
plt.plot(range(tm + 1), r, label='Setpoint')
plt.xlabel('Time')
plt.ylabel('Weight')
plt.title('kp=0.01, ki=1')
plt.legend()
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# 状態空間モデルの定義
A = np.array([[0, 1],
[-2, -3]])
B = np.array([[0],
[1]])
C = np.array([[1, 0]])
D = np.array([[0]])
# 状態変数線図をプロット
def plot_state_variable_diagram(A, B, C, D):
G = nx.DiGraph()
num_states = A.shape[0]
num_inputs = B.shape[1]
num_outputs = C.shape[0]
# ノードの追加
for i in range(num_states):
G.add_node(f'x{i}', pos=(1, i))
for i in range(num_inputs):
G.add_node(f'u{i}', pos=(0, i))
for i in range(num_outputs):
G.add_node(f'y{i}', pos=(2, i))
# エッジの追加
for i in range(num_states):
G.add_edge(f'x{i}', f'x{i}', label=f'x{i}\'')
for i in range(num_states):
for j in range(num_states):
if A[j, i] != 0:
G.add_edge(f'x{i}', f'x{j}', label=f'A[{j},{i}] = {A[j,i]}')
for i in range(num_states):
for j in range(num_inputs):
if B[i, j] != 0:
G.add_edge(f'u{j}', f'x{i}', label=f'B[{i},{j}] = {B[i,j]}')
for i in range(num_states):
for j in range(num_outputs):
if C[j, i] != 0:
G.add_edge(f'x{i}', f'y{j}', label=f'C[{j},{i}] = {C[j,i]}')
# プロット
pos = nx.get_node_attributes(G, 'pos')
labels = nx.get_edge_attributes(G, 'label')
plt.figure(figsize=(10, 6))
nx.draw(G, pos, with_labels=True, node_size=2000, node_color='lightblue', font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.title('State Variable Diagram')
plt.show()
# 状態変数変換(例: 状態空間モデルの変換)
def state_variable_transformation(A, B, C, transformation_matrix):
A_new = np.linalg.inv(transformation_matrix) @ A @ transformation_matrix
B_new = np.linalg.inv(transformation_matrix) @ B
C_new = C @ transformation_matrix
return A_new, B_new, C_new
# 変換行列の定義(例として単位行列を使用)
transformation_matrix = np.eye(A.shape[0])
# 状態変数線図をプロット
plot_state_variable_diagram(A, B, C, D)
# 状態変数変換の実行
A_new, B_new, C_new = state_variable_transformation(A, B, C, transformation_matrix)
print("Original A matrix:\n", A)
print("Transformed A matrix:\n", A_new)
print("Original B matrix:\n", B)
print("Transformed B matrix:\n", B_new)
print("Original C matrix:\n", C)
print("Transformed C matrix:\n", C_new)
import numpy as np
import scipy.linalg as linalg
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# 状態空間モデルの定義
A = np.array([[0, 1],
[-2, -2]])
B = np.array([[0],
[1]])
C = np.array([[1, 0]])
D = np.array([[0]])
# LQR設計のための評価関数行列
Q = np.eye(2) # 状態の重み行列
R = np.array([[1]]) # 入力の重み行列
# リカッチ方程式を解く
def lqr(A, B, Q, R):
P = linalg.solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R) @ B.T @ P
return K
# 最適制御則
K = lqr(A, B, Q, R)
# システム応答の計算
def system_response(A, B, C, D, K, t, x0):
def dynamics(x, t):
u = -K @ x
dxdt = A @ x + B @ u
return dxdt
sol = odeint(dynamics, x0, t)
y = C @ sol.T + D @ (-K @ sol.T)
return sol, y
# 評価関数の計算
def compute_cost(A, B, Q, R, x0, K, t):
def integrand(x, t):
u = -K @ x
return np.dot(x.T, Q @ x) + np.dot(u.T, R @ u)
x_t, _ = system_response(A, B, C, D, K, t, x0)
cost = np.trapz([integrand(x, t_i) for x, t_i in zip(x_t, t)], t)
return cost
# シミュレーションの設定
t = np.linspace(0, 10, 500)
x0 = np.array([1, 0]) # 初期状態
# システムの応答
x_t, y_t = system_response(A, B, C, D, K, t, x0)
# 評価関数の計算
cost = compute_cost(A, B, Q, R, x0, K, t)
print(f'Optimal Cost: {cost}')
# 応答のプロット
plt.figure(figsize=(14, 8))
plt.subplot(2, 1, 1)
plt.plot(t, y_t.T)
plt.title('System Output with Optimal Control')
plt.xlabel('Time [s]')
plt.ylabel('Output')
plt.grid()
plt.subplot(2, 1, 2)
plt.plot(t, x_t[:, 0], label='State x1')
plt.plot(t, x_t[:, 1], label='State x2')
plt.title('State Variables with Optimal Control')
plt.xlabel('Time [s]')
plt.ylabel('State Values')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# データの読み込み(例としてサンプルデータを生成します)
frequencies = np.logspace(1, 5, num=100)
Z_real = 100 + 10 / (frequencies ** 0.5) # 実部
Z_imag = -20 / (frequencies ** 0.5) # 虚部
Z = Z_real + 1j * Z_imag
# ニクィストプロットの作成
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(Z_real, -Z_imag, 'o')
plt.xlabel('Real(Z) [Ohm]')
plt.ylabel('-Imag(Z) [Ohm]')
plt.title('Nyquist Plot')
plt.grid(True)
plt.axis('equal')
# ボードプロットの作成
plt.subplot(1, 2, 2)
plt.loglog(frequencies, np.abs(Z), 'o', label='|Z|')
plt.loglog(frequencies, np.abs(np.angle(Z, deg=True)), 'o', label='Phase')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude |Z| [Ohm] / Phase [deg]')
plt.title('Bode Plot')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# EISデータのモデルフィッティング
def impedance_model(f, R, C):
omega = 2 * np.pi * f
Z = R + 1 / (1j * omega * C)
return np.abs(Z)
# 初期推定値
initial_guess = [100, 1e-6]
# カーブフィットの実行
popt, pcov = curve_fit(impedance_model, frequencies, np.abs(Z), p0=initial_guess)
# フィット結果の表示
R_fit, C_fit = popt
print(f'Fitted R: {R_fit} Ohm')
print(f'Fitted C: {C_fit} F')
# フィット結果のプロット
Z_fit = impedance_model(frequencies, R_fit, C_fit)
plt.figure(figsize=(10, 5))
plt.loglog(frequencies, np.abs(Z), 'o', label='Measured |Z|')
plt.loglog(frequencies, Z_fit, '-', label='Fitted |Z|')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude |Z| [Ohm]')
plt.title('Bode Plot with Fit')
plt.grid(True)
plt.legend()
plt.show()
import numpy as np
# 定義
n_states = 10 # 状態の数
n_actions = 2 # アクションの数
gamma = 0.9 # 割引因子
tolerance = 1e-6
# 状態遷移関数とコスト関数の定義
def f(x, u):
return (x + u) % n_states # 状態遷移の例
def c(x, u):
return (x - u) ** 2 # コスト関数の例
# ベルマン方程式を解くための価値関数の初期化
V = np.zeros(n_states)
V_new = np.zeros(n_states)
# ベルマン方程式の反復計算
while True:
for x in range(n_states):
min_value = float('inf')
for u in range(n_actions):
next_state = f(x, u)
value = c(x, u) + gamma * V[next_state]
if value < min_value:
min_value = value
V_new[x] = min_value
# 収束判定
if np.max(np.abs(V_new - V)) < tolerance:
break
V = np.copy(V_new)
print("最適価値関数 V(x):")
print(V)
import numpy as np
import matplotlib.pyplot as plt
# 定数の設定
m1, m2 = 1.0, 1.0 # リンクの質量
l1, l2 = 1.0, 1.0 # リンクの長さ
r1, r2 = 0.5, 0.5 # 重心位置
I1, I2 = 0.1, 0.1 # 慣性テンソル
g = 9.81 # 重力加速度
# 状態とトルクの設定
theta1, theta2 = np.pi / 4, np.pi / 4 # 関節角
theta1_dot, theta2_dot = 0, 0 # 関節角速度
tau1, tau2 = 0, 0 # トルク
# マトリックスの設定
M11 = m1 * r1**2 + m2 * (l1**2 + r2**2 + 2 * l1 * r2 * np.cos(theta2)) + I1 + I2
M12 = m2 * (r2**2 + l1 * r2 * np.cos(theta2)) + I2
M21 = M12
M22 = m2 * r2**2 + I2
# コリオリ・遠心力
C1 = -m2 * l1 * r2 * np.sin(theta2) * theta2_dot
C2 = m2 * l1 * r2 * np.sin(theta2) * theta1_dot
# 重力項
G1 = (m1 * r1 + m2 * l1) * g * np.cos(theta1) + m2 * g * r2 * np.cos(theta1 + theta2)
G2 = m2 * g * r2 * np.cos(theta1 + theta2)
# 運動方程式
theta_ddot = np.linalg.inv(np.array([[M11, M12], [M21, M22]])) @ (np.array([tau1 - C1 - G1, tau2 - C2 - G2]))
# プロット
plt.figure(figsize=(10, 6))
plt.plot([0, l1 * np.cos(theta1)], [0, l1 * np.sin(theta1)], 'r-', label='Link 1')
plt.plot([l1 * np.cos(theta1), l1 * np.cos(theta1) + l2 * np.cos(theta1 + theta2)],
[l1 * np.sin(theta1), l1 * np.sin(theta1) + l2 * np.sin(theta1 + theta2)], 'b-', label='Link 2')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Robot Arm Configuration')
plt.legend()
plt.grid(True)
plt.show()
print(f"Joint accelerations: θ1_ddot = {theta_ddot[0]:.2f}, θ2_ddot = {theta_ddot[1]:.2f}")
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sympy import symbols, diff, cos, sin
# Define symbols
q1, q2, q1_dot, q2_dot = symbols('q1 q2 q1_dot q2_dot')
l1, l2, m1, m2, g = symbols('l1 l2 m1 m2 g')
# Define positions
x1 = l1 * sin(q1)
y1 = -l1 * cos(q1)
x2 = x1 + l2 * sin(q1 + q2)
y2 = y1 - l2 * cos(q1 + q2)
# Calculate kinetic and potential energy
T1 = 0.5 * m1 * (x1.diff(q1)**2 + y1.diff(q1)**2) * q1_dot**2
T2 = 0.5 * m2 * (x2.diff(q1)**2 + y2.diff(q1)**2) * q1_dot**2 + (x2.diff(q2)**2 + y2.diff(q2)**2) * q2_dot**2
T = T1 + T2
V1 = m1 * g * y1
V2 = m2 * g * y2
V = V1 + V2
# Lagrangian function
L = T - V
# Compute equations of motion
L_q1 = diff(L, q1)
L_q1_dot = diff(L, q1_dot)
L_q2 = diff(L, q2)
L_q2_dot = diff(L, q2_dot)
d_dt_L_q1_dot = diff(L_q1_dot, q1) * q1_dot + diff(L_q1_dot, q2) * q2_dot
d_dt_L_q2_dot = diff(L_q2_dot, q1) * q1_dot + diff(L_q2_dot, q2) * q2_dot
eq1 = d_dt_L_q1_dot - L_q1
eq2 = d_dt_L_q2_dot - L_q2
# Parameters for visualization
params = {
l1: 1.0, l2: 1.0, m1: 1.0, m2: 1.0, g: 9.81,
q1_dot: 0.0, q2_dot: 0.0
}
# Create a grid for theta1 and theta2
theta1_vals = np.linspace(-np.pi, np.pi, 100)
theta2_vals = np.linspace(-np.pi, np.pi, 100)
THETA1, THETA2 = np.meshgrid(theta1_vals, theta2_vals)
# Compute the end-effector position
X = params[l1] * np.sin(THETA1) + params[l2] * np.sin(THETA1 + THETA2)
Y = -params[l1] * np.cos(THETA1) - params[l2] * np.cos(THETA1 + THETA2)
Z = np.zeros_like(X) # For visualization, Z can be set to zero or any other value if needed
# Plot
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='k')
ax.set_xlabel('X Position')
ax.set_ylabel('Y Position')
ax.set_zlabel('Z Position')
ax.set_title('Workspace of a 2-Link Robot Arm')
plt.show()
メモ
https://www.docswell.com/s/m_shimojo/ZM1DQW-2024-03-15-135220#p1