コピペで学ぶ機械学習

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# Irisデータセットの読み込み
iris = datasets.load_iris()
X = iris.data[:, :2]  # 最初の2つの特徴量を使用
y = iris.target

# データセットを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# サポートベクターマシンの定義
svm_classifier = SVC(kernel='linear', C=1.0, random_state=42)

# モデルの訓練
svm_classifier.fit(X_train, y_train)

# テストデータで予測
y_pred = svm_classifier.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")

# メッシュの作成
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                     np.arange(y_min, y_max, 0.01))

# 各点での予測値を計算
Z = svm_classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# データと決定境界のプロット
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', s=20)
plt.title('Support Vector Machine')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数とその微分の定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

# 入力範囲の定義
x = np.linspace(-5, 5, 100)  # -5から5までの範囲を100点で分割

# シグモイド関数とその微分の計算
sigmoid_values = sigmoid(x)
sigmoid_derivative_values = sigmoid_derivative(x)

# プロットの設定
plt.figure(figsize=(10, 5))

# シグモイド関数のプロット
plt.subplot(1, 2, 1)
plt.plot(x, sigmoid_values, label='sigmoid(x)')
plt.title('Sigmoid Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.legend()

# シグモイド関数の微分のプロット
plt.subplot(1, 2, 2)
plt.plot(x, sigmoid_derivative_values, label='sigmoid\'(x)')
plt.title('Derivative of Sigmoid Function')
plt.xlabel('x')
plt.ylabel('sigmoid\'(x)')
plt.grid(True)
plt.legend()

# グラフの表示
plt.tight_layout()
plt.show()

import numpy as np

def hadamard_matrix(n):
    if n == 1:
        return np.array([[1]])
    else:
        H_half = hadamard_matrix(n // 2)
        H = np.block([[H_half, H_half],
                      [H_half, -H_half]])
        return H

n = 4  # 生成する行列のサイズ
H = hadamard_matrix(n)
print("Hadamard Matrix of size", n, ":\n", H)

import numpy as np

# Example matrix and vector
A = np.array([[4, 2, -1],
              [2, 3, 0],
              [-1, 0, 1]])
x = np.array([1, 2, 3])

# Symmetric part
A_S = 0.5 * (A + A.T)
# Antisymmetric part
A_A = 0.5 * (A - A.T)

# Verify decomposition
A_reconstructed = A_S + A_A

# Quadratic forms
quadratic_form_A = x.T @ A @ x
quadratic_form_A_S = x.T @ A_S @ x
quadratic_form_A_A = x.T @ A_A @ x

# Print results
print("Original matrix A:")
print(A)
print("\nSymmetric part A_S:")
print(A_S)
print("\nAntisymmetric part A_A:")
print(A_A)
print("\nReconstructed matrix A (should be equal to original A):")
print(A_reconstructed)
print("\nQuadratic form x^T A x:")
print(quadratic_form_A)
print("\nQuadratic form x^T A_S x (should be equal to x^T A x):")
print(quadratic_form_A_S)
print("\nQuadratic form x^T A_A x (should be zero):")
print(quadratic_form_A_A)

import numpy as np

# Define vectors x and y
x = np.array([1.0, 2.0, 3.0])
y = np.array([4.0, 5.0, 6.0])

# Inner product
inner_product = np.dot(x, y)

# Gradient of the inner product with respect to x and y
grad_inner_product_x = y
grad_inner_product_y = x

print("Inner product x^T y:", inner_product)
print("Gradient with respect to x:", grad_inner_product_x)
print("Gradient with respect to y:", grad_inner_product_y)

# Define a square matrix A
A = np.array([[1.0, 2.0, 3.0],
              [2.0, 4.0, 5.0],
              [3.0, 5.0, 6.0]])

# Quadratic form
quadratic_form = np.dot(x.T, np.dot(A, x))

# Gradient of the quadratic form with respect to x
grad_quadratic_form = np.dot(A + A.T, x)

# If A is symmetric
if np.allclose(A, A.T):
    grad_quadratic_form_symmetric = 2 * np.dot(A, x)
else:
    grad_quadratic_form_symmetric = "A is not symmetric"

print("\nQuadratic form x^T A x:", quadratic_form)
print("Gradient of the quadratic form:", grad_quadratic_form)
print("Gradient of the quadratic form (if A is symmetric):", grad_quadratic_form_symmetric)

import numpy as np
from sklearn.linear_model import Ridge, Lasso, ElasticNet

# Generate some data
np.random.seed(42)
X = np.random.randn(100, 5)
w_true = np.array([1.5, -2.0, 0.5, 1.0, -1.5])
y = X.dot(w_true) + np.random.randn(100)

# Regularization parameters
lambda_ridge = 1.0
lambda_lasso = 1.0
alpha_elasticnet = 1.0
l1_ratio_elasticnet = 0.5

# Ridge Regression
ridge = Ridge(alpha=lambda_ridge, fit_intercept=False)
ridge.fit(X, y)
print("Ridge regression coefficients:", ridge.coef_)

# Lasso Regression
lasso = Lasso(alpha=lambda_lasso, fit_intercept=False)
lasso.fit(X, y)
print("Lasso regression coefficients:", lasso.coef_)

# Elastic Net Regression
elastic_net = ElasticNet(alpha=alpha_elasticnet, l1_ratio=l1_ratio_elasticnet, fit_intercept=False)
elastic_net.fit(X, y)
print("Elastic Net regression coefficients:", elastic_net.coef_)

# Multidimensional Target Ridge Regression
Y = np.random.randn(100, 3)  # 3-dimensional target
ridge_multidim = Ridge(alpha=lambda_ridge, fit_intercept=False)
ridge_multidim.fit(X, Y)
print("Ridge regression coefficients (multidimensional target):")
print(ridge_multidim.coef_)

# 必要なライブラリをインポートする
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# データセットをロードする
iris = load_iris()
X = iris.data
y = iris.target

# データを訓練用とテスト用に分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ランダムフォレストの分類器を作成する
rf_classifier = RandomForestClassifier(n_estimators=100, random_state=42)

# モデルを訓練する
rf_classifier.fit(X_train, y_train)

# テストデータで予測を行う
y_pred = rf_classifier.predict(X_test)

# 正解率を計算する
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy}')

import numpy as np

# ベクトル x を定義
x = np.array([1, 2, 3])

# 重みベクトル w を定義
w = np.array([0.5, 0.2, 0.8])

# 行列 A を定義
A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])

# 関数 f(x) の定義 (例として、二乗和)
def f(x):
    return np.sum(x**2)

# 関数 f(x) の勾配を計算する関数
def gradient_f(x):
    return 2 * x

# 線形結合 y を計算
y = np.dot(w, x)

# 2次形式 z を計算
z = np.dot(x, np.dot(A, x))

# 関数 f(x) の勾配を計算
grad_f_x = gradient_f(x)

# 結果の出力
print("線形結合 y:", y)
print("2次形式 z:", z)
print("関数の勾配:", grad_f_x)

import numpy as np

# サンプル入力と重み、バイアスの初期化
input_data = np.array([0.5, 0.3, 0.2])  # 入力データ
weights = np.array([[0.1, 0.2, 0.3],
                    [0.2, 0.3, 0.4],
                    [0.3, 0.4, 0.5]])  # 重み行列
biases = np.array([0.1, 0.2, 0.3])  # バイアスベクトル

# 関数の定義
def forward_propagation(input_data, weights, biases):
    z = np.dot(weights, input_data) + biases
    return z

# 順伝播（forward propagation）
output = forward_propagation(input_data, weights, biases)
print("順伝播出力:", output)

# ヤコビアン行列の計算（全微分行列）
def jacobian_matrix(weights, input_data):
    return weights

# ヤコビアン行列の計算
J = jacobian_matrix(weights, input_data)
print("ヤコビアン行列:\n", J)

# 逆伝播（バックプロパゲーション）による勾配の計算
# 仮の誤差逆伝搬法の例として、出力の勾配を求める場合
output_gradient = np.array([1.0, 1.0, 1.0])  # 出力の勾配（仮の値）
input_gradient = np.dot(J.T, output_gradient)  # 入力の勾配の計算
print("入力の勾配:", input_gradient)

import numpy as np
import matplotlib.pyplot as plt

# 線形ガウスモデルの設定
A = np.array([[1, 1],
              [0, 1]])  # 状態遷移行列
C = np.array([[1, 0]])  # 観測行列
Q = np.eye(2) * 0.01  # 状態遷移ノイズの共分散行列
R = np.eye(1) * 0.1   # 観測ノイズの共分散行列

# 真の状態と観測データの生成
np.random.seed(0)
n = 50  # サンプル数
true_state = np.zeros((2, n))
observations = np.zeros((1, n))

for t in range(1, n):
    true_state[:, t] = np.dot(A, true_state[:, t-1]) + np.random.multivariate_normal([0, 0], Q)
    observations[:, t] = np.dot(C, true_state[:, t]) + np.random.normal(0, np.sqrt(R[0, 0]))

# 最尤推定による状態推定
def linear_regression_MLE(X, y):
    theta_hat = np.linalg.inv(X.T @ X) @ X.T @ y
    return theta_hat

# カルマンフィルタによる状態推定
def kalman_filter(A, C, Q, R, observations):
    n = observations.shape[1]
    state_means = np.zeros((2, n))
    state_covs = np.zeros((2, 2, n))
    
    # 初期化
    initial_state_mean = np.zeros(2)
    initial_state_covariance = np.eye(2)
    
    state_means[:, 0] = initial_state_mean
    state_covs[:, :, 0] = initial_state_covariance
    
    for t in range(1, n):
        # 予測ステップ
        predicted_state_mean = np.dot(A, state_means[:, t-1])
        predicted_state_covariance = np.dot(np.dot(A, state_covs[:, :, t-1]), A.T) + Q
        
        # 更新ステップ
        innovation = observations[:, t] - np.dot(C, predicted_state_mean)
        innovation_covariance = np.dot(np.dot(C, predicted_state_covariance), C.T) + R
        
        kalman_gain = np.dot(np.dot(predicted_state_covariance, C.T), np.linalg.inv(innovation_covariance))
        
        state_means[:, t] = predicted_state_mean + np.dot(kalman_gain, innovation)
        state_covs[:, :, t] = predicted_state_covariance - np.dot(np.dot(kalman_gain, C), predicted_state_covariance)
    
    return state_means

# パラメータの推定
X = np.vstack((np.ones(n), observations)).T
theta_hat_mle = linear_regression_MLE(X, true_state[0, :])

# カルマンフィルタによる状態推定
kalman_means = kalman_filter(A, C, Q, R, observations)

# 結果のプロット
plt.figure(figsize=(12, 6))
plt.plot(true_state[0, :], label='True State 1', linestyle='--')
plt.plot(theta_hat_mle[0] + observations.flatten(), label='MLE + Observations', linestyle='-.')
plt.plot(kalman_means[0, :], label='Kalman Filter', linestyle='-')
plt.title('Comparison of MLE and Kalman Filter for State Estimation')
plt.xlabel('Time')
plt.ylabel('State')
plt.legend()
plt.grid(True)
plt.show()

def bayes_theorem(prior_A, likelihood_B_given_A, prior_B):
    # P(B|A) * P(A)
    numerator = likelihood_B_given_A * prior_A
    
    # P(B)
    denominator = prior_B
    
    # P(A|B) = (P(B|A) * P(A)) / P(B)
    posterior_A = numerator / denominator
    
    return posterior_A

# 例: 病気の発症確率
# 事前確率: P(A) = 0.01 (病気の発症率)
prior_A = 0.01

# P(B|A): 病気の発症者が陽性と診断される確率 (感度)
likelihood_B_given_A = 0.95

# P(B): テストが陽性となる確率 (全体の陽性率)
# P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
# ここでは、簡単のためにP(B|not A)を0.05と仮定し、P(not A)を計算します。
likelihood_B_given_not_A = 0.05
prior_not_A = 1 - prior_A
prior_B = (likelihood_B_given_A * prior_A) + (likelihood_B_given_not_A * prior_not_A)

# ベイズ定理を用いて事後確率 P(A|B) を計算
posterior_A = bayes_theorem(prior_A, likelihood_B_given_A, prior_B)

print(f'事前確率 P(A) = {prior_A}')
print(f'P(B|A) = {likelihood_B_given_A}')
print(f'P(B) = {prior_B}')
print(f'事後確率 P(A|B) = {posterior_A}')

import numpy as np
import matplotlib.pyplot as plt

# ソフトマックス関数
def softmax(z):
    exp_z = np.exp(z - np.max(z))
    return exp_z / exp_z.sum(axis=0)

# ソフトマックス関数の偏微分
def softmax_derivative(z):
    s = softmax(z)
    s = s.reshape(-1, 1)
    jacobian = np.diagflat(s) - np.dot(s, s.T)
    return jacobian

# 入力ベクトル
z = np.linspace(-2, 2, 100)

# ソフトマックス関数の計算
s = np.array([softmax(np.array([x, 1, 0]))[0] for x in z])

# ソフトマックス関数の偏微分の計算
ds = np.array([softmax_derivative(np.array([x, 1, 0]))[0, 0] for x in z])

# プロット
fig, ax = plt.subplots(1, 2, figsize=(14, 6))

# ソフトマックス関数のプロット
ax[0].plot(z, s)
ax[0].set_title('Softmax Function')
ax[0].set_xlabel('Input')
ax[0].set_ylabel('Output')

# ソフトマックス関数の偏微分のプロット
ax[1].plot(z, ds)
ax[1].set_title('Derivative of Softmax Function')
ax[1].set_xlabel('Input')
ax[1].set_ylabel('Derivative')

plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# 2次元のガウス関数の定義
def gaussian_2d(x, y, mean, cov):
    pos = np.dstack((x, y))
    rv = multivariate_normal(mean, cov)
    return rv.pdf(pos)

# 入力ベクトルの範囲
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)

# 平均パラメータと共分散行列
mean = [0, 0]
cov = [[1, 0], [0, 1]]

# ガウス関数の計算
z = gaussian_2d(x, y, mean, cov)

# プロット
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

ax.set_title('2D Gaussian Function')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Probability Density')

plt.show()

# 積分して1になることの確認
integral = np.trapz(np.trapz(z, y, axis=0), x, axis=0)
print(f'Integral: {integral}')

import numpy as np
import matplotlib.pyplot as plt

# データの生成
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# バイアス項を追加
X_b = np.c_[np.ones((100, 1)), X]

# パラメータの初期化
theta = np.random.randn(2, 1)

# 学習率
eta = 0.1
# イテレーションの回数
n_iterations = 1000
# サンプルサイズ
m = 100

# 平均二乗誤差の計算
def compute_mse(X, y, theta):
    predictions = X.dot(theta)
    mse = (1/m) * np.sum((predictions - y) ** 2)
    return mse

# 勾配降下法
for iteration in range(n_iterations):
    gradients = (2/m) * X_b.T.dot(X_b.dot(theta) - y)
    theta = theta - eta * gradients

# 最終的なパラメータ
print("Theta:", theta)

# MSEの計算
mse = compute_mse(X_b, y, theta)
print("MSE:", mse)

# 結果のプロット
plt.plot(X, y, "b.")
plt.plot(X, X_b.dot(theta), "r-")
plt.xlabel("X")
plt.ylabel("y")
plt.title("Linear Regression with Gradient Descent")
plt.show()

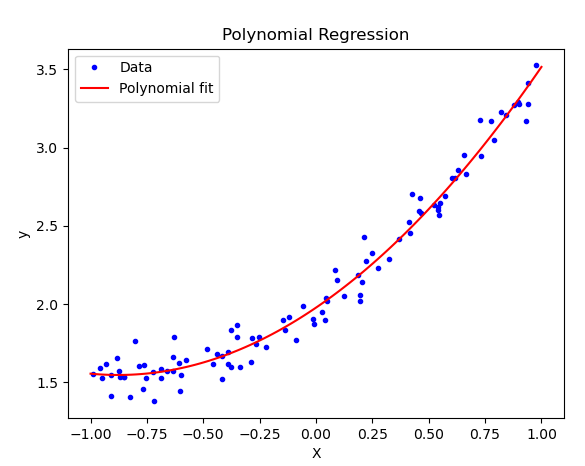
import numpy as np
import matplotlib.pyplot as plt

# データの生成
np.random.seed(42)
X = 2 * np.random.rand(100, 1) - 1  # [-1, 1]の範囲
y = 0.5 * X**2 + X + 2 + np.random.randn(100, 1) * 0.1

# 基底関数の定義（ここでは多項式基底関数を使用）
def polynomial_features(X, degree):
    return np.hstack([X**i for i in range(degree + 1)])

# デザイン行列の作成
degree = 2  # 多項式の次数
X_poly = polynomial_features(X, degree)

# パラメータの最適化（最小二乗法）
theta_best = np.linalg.inv(X_poly.T.dot(X_poly)).dot(X_poly.T).dot(y)

# 予測関数
def predict(X, theta):
    X_poly = polynomial_features(X, degree)
    return X_poly.dot(theta)

# データのプロット
plt.plot(X, y, "b.", label="Data")
X_fit = np.linspace(-1, 1, 100).reshape(100, 1)
y_fit = predict(X_fit, theta_best)
plt.plot(X_fit, y_fit, "r-", label="Polynomial fit")
plt.xlabel("X")
plt.ylabel("y")
plt.title("Polynomial Regression")
plt.legend()
plt.show()

# 最適化されたパラメータ
print("Optimal parameters:", theta_best.ravel())

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# データの生成
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2,
                           n_clusters_per_class=1, random_state=42)

# データの可視化
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, s=50, edgecolor='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Generated Data for Binary Classification')
plt.colorbar()
plt.show()

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの作成と学習
model = LogisticRegression()
model.fit(X_train, y_train)

# テストデータを用いた予測
y_pred = model.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# 決定境界のプロット
def plot_decision_boundary(model, X, y):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.RdBu)
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.RdBu, s=50)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.title('Decision Boundary')
    plt.colorbar()

# 決定境界のプロット
plt.figure(figsize=(8, 6))
plot_decision_boundary(model, X, y)
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = (4 + 3 * X + np.random.randn(100, 1)).ravel()

# データのプロット
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Generated Data')
plt.show()

# パラメータの初期化
theta = np.random.randn(2, 1)  # バイアス項と重みの初期値

# バイアス項の追加
X_b = np.c_[np.ones((100, 1)), X]

# 学習率とエポック数
eta = 0.1
n_iterations = 1000

# 勾配降下法の実装
for iteration in range(n_iterations):
    gradients = 2/100 * X_b.T.dot(X_b.dot(theta) - y.reshape(-1, 1))
    theta = theta - eta * gradients

# 学習結果の表示
print("学習後のパラメータ:")
print(theta)

# データと学習した直線のプロット
plt.scatter(X, y)
plt.plot(X, X_b.dot(theta), color='red', label='Predictions')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Gradient Descent')
plt.legend()
plt.show()

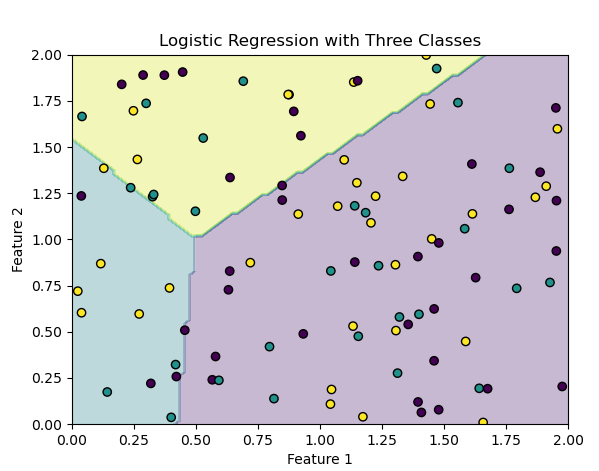
import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(100, 2)
y = np.random.randint(0, 3, size=100)

# データのプロット
plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', marker='o', label='Class 0')
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue', marker='x', label='Class 1')
plt.scatter(X[y == 2, 0], X[y == 2, 1], color='green', marker='s', label='Class 2')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Generated Data')
plt.legend()
plt.show()

# ダミー入力の追加
X_b = np.c_[np.ones((100, 1)), X]  # ダミー入力として1の列を追加

# パラメータの初期化
eta = 0.1  # 学習率
n_iterations = 1000
n_inputs = X_b.shape[1]  # 入力の数（特徴量数 + バイアス項）

# クラスごとの重みベクトルの初期化
theta = np.random.randn(n_inputs, 3)

# シグモイド関数の定義
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 交差エントロピー誤差の計算
def compute_loss(theta, X_b, y):
    logits = X_b.dot(theta)
    y_prob = sigmoid(logits)
    losses = -np.mean(np.sum((np.eye(3)[y] * np.log(y_prob)), axis=1))
    return losses

# 勾配降下法の実装
for iteration in range(n_iterations):
    logits = X_b.dot(theta)
    y_prob = sigmoid(logits)
    gradients = 1/100 * X_b.T.dot(y_prob - np.eye(3)[y])
    theta = theta - eta * gradients

# モデルの学習結果の表示
print("学習後のパラメータ:")
print(theta)

# データと境界線のプロット
x0, x1 = np.meshgrid(np.linspace(0, 2, 100), np.linspace(0, 2, 100))
X_new = np.c_[np.ones((10000, 1)), x0.ravel(), x1.ravel()]
y_proba = sigmoid(X_new.dot(theta))
y_predict = np.argmax(y_proba, axis=1)

plt.contourf(x0, x1, y_predict.reshape(100, 100), alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression with Three Classes')
plt.show()

import numpy as np

# シグモイド関数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# ソフトマックス関数
def softmax(x):
    exp_scores = np.exp(x)
    return exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

# 交差エントロピー誤差
def cross_entropy_loss(y, y_pred):
    m = y.shape[0]
    log_likelihood = -np.log(y_pred[range(m), y])
    loss = np.sum(log_likelihood) / m
    return loss

# 数値微分法
def numerical_gradient(f, x, epsilon=1e-5):
    grad = np.zeros_like(x)
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        orig_val = x[idx]
        x[idx] = orig_val + epsilon
        fx_plus_epsilon = f(x)
        x[idx] = orig_val - epsilon
        fx_minus_epsilon = f(x)
        grad[idx] = (fx_plus_epsilon - fx_minus_epsilon) / (2 * epsilon)
        x[idx] = orig_val
        it.iternext()
    return grad

# ニューラルネットワークの定義
class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        
        # 重みの初期化
        self.W1 = np.random.randn(input_size, hidden_size)
        self.b1 = np.zeros((1, hidden_size))
        self.W2 = np.random.randn(hidden_size, output_size)
        self.b2 = np.zeros((1, output_size))
        
    def forward_propagation(self, X):
        # 入力層から中間層への順伝播
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = sigmoid(self.z1)
        
        # 中間層から出力層への順伝播
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = softmax(self.z2)
        
        return self.a2
    
    def backward_propagation(self, X, y, learning_rate=0.1):
        m = X.shape[0]
        
        # 出力層での誤差
        delta3 = self.a2
        delta3[range(m), y] -= 1
        delta3 /= m
        
        # 出力層から中間層への勾配
        dW2 = np.dot(self.a1.T, delta3)
        db2 = np.sum(delta3, axis=0, keepdims=True)
        
        # 中間層での誤差
        delta2 = np.dot(delta3, self.W2.T) * (self.a1 * (1 - self.a1))
        
        # 入力層から中間層への勾配
        dW1 = np.dot(X.T, delta2)
        db1 = np.sum(delta2, axis=0)
        
        # パラメータの更新
        self.W1 -= learning_rate * dW1
        self.b1 -= learning_rate * db1
        self.W2 -= learning_rate * dW2
        self.b2 -= learning_rate * db2
        
    def train(self, X, y, epochs=1000, learning_rate=0.1):
        for epoch in range(epochs):
            # 順伝播と逆伝播
            y_pred = self.forward_propagation(X)
            self.backward_propagation(X, y, learning_rate)
            
            # 誤差の計算（平均交差エントロピー誤差）
            if epoch % 100 == 0:
                loss = cross_entropy_loss(y, y_pred)
                print(f'Epoch {epoch}, Loss: {loss}')
    
    def predict(self, X):
        return np.argmax(self.forward_propagation(X), axis=1)

# データの準備
np.random.seed(0)
X = np.random.randn(100, 2)
y = np.random.randint(0, 3, size=100)

# モデルの定義と学習
model = NeuralNetwork(input_size=2, hidden_size=5, output_size=3)
model.train(X, y, epochs=1000, learning_rate=0.1)

# テストデータでの予測
y_pred = model.predict(X)

# 結果の表示
accuracy = np.mean(y_pred == y)
print(f'Accuracy: {accuracy}')

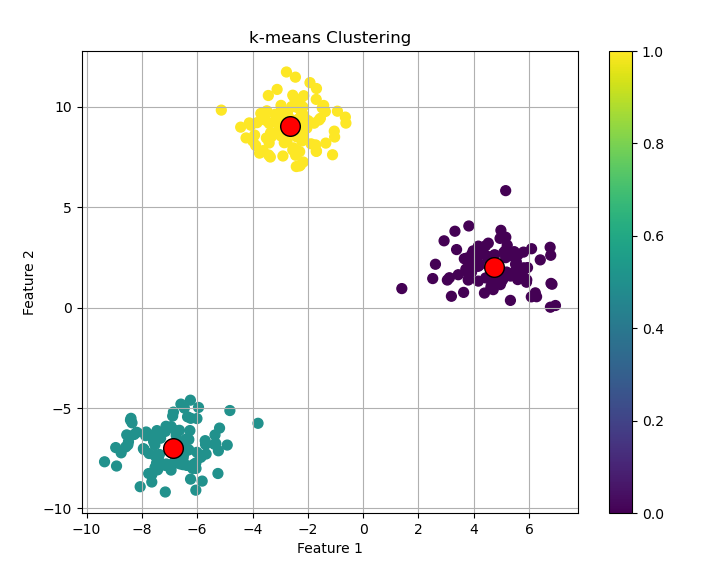
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# Generate dummy data
n_samples = 300
n_clusters = 3
random_state = 42

X, y = make_blobs(n_samples=n_samples, centers=n_clusters, random_state=random_state)

# Apply k-means clustering
kmeans = KMeans(n_clusters=n_clusters, random_state=random_state)
kmeans.fit(X)

# Get cluster centers
centers = kmeans.cluster_centers_
print(f"Cluster centers:\n{centers}")

# Plot the clustering result
plt.figure(figsize=(8, 6))

plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], marker='o', c='red', s=200, edgecolor='k')

plt.title('k-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.colorbar()
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from scipy.stats import norm

# True parameters
true_mean = 5.0
true_std = 2.0

# Generate observed data
np.random.seed(0)
data = np.random.normal(true_mean, true_std, 100)

# MAP estimation function
def map_estimation(data, prior_mean, prior_std, likelihood_std):
    # Likelihood function P(D|theta): Gaussian likelihood
    def likelihood(theta):
        return np.prod(norm.pdf(data, loc=theta, scale=likelihood_std))
    
    # Prior distribution P(theta): Gaussian prior
    def prior(theta):
        return norm.pdf(theta, loc=prior_mean, scale=prior_std)
    
    # Posterior log probability
    def posterior_log(theta):
        return np.log(likelihood(theta)) + np.log(prior(theta))
    
    # Optimize to maximize posterior
    result = minimize(lambda x: -posterior_log(x), prior_mean)
    map_estimate = result.x[0]
    
    return map_estimate

# Initial estimates
prior_mean = 0.0   # Prior mean
prior_std = 10.0   # Prior standard deviation
likelihood_std = true_std  # Likelihood standard deviation (assuming same as true std)

# Perform MAP estimation
map_estimate = map_estimation(data, prior_mean, prior_std, likelihood_std)

# Print the MAP estimated mean
print(f'MAP estimated mean: {map_estimate}')

# Plotting results
plt.figure(figsize=(10, 6))
plt.hist(data, bins=20, density=True, alpha=0.7, label='Histogram of Observed Data')
x = np.linspace(np.min(data), np.max(data), 100)
plt.plot(x, norm.pdf(x, true_mean, true_std), 'r-', label='True Distribution')
plt.plot(x, norm.pdf(x, map_estimate, true_std), 'g--', label='MAP Estimated Distribution')
plt.title('MAP Estimation of Gaussian Mean')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.linalg import inv

# Parameters
true_amplitude = 3.0
true_frequency = 0.1
true_phase = np.pi / 2
true_noise_std = 1.0
quantization_levels = 256  # 8-bit ADC levels

# Generate true signal (sinusoidal with noise)
np.random.seed(0)
t = np.linspace(0, 10, 1000)
true_signal = true_amplitude * np.sin(2 * np.pi * true_frequency * t + true_phase)
noise = np.random.normal(0, true_noise_std, t.shape)
noisy_signal = true_signal + noise

# Quantize noisy signal (8-bit ADC simulation)
quantized_signal = np.round((noisy_signal - np.min(noisy_signal)) / (np.max(noisy_signal) - np.min(noisy_signal)) * (quantization_levels - 1))
quantized_signal = quantized_signal / (quantization_levels - 1) * (np.max(noisy_signal) - np.min(noisy_signal)) + np.min(noisy_signal)

# Kalman Filter Initialization
# Initial state estimate
x_hat = np.array([0.0, 0.0])  # [amplitude, frequency]
# Initial covariance matrix (uncertainty)
P = np.diag([1.0, 1.0])

# Process noise covariance (Q)
Q = np.diag([0.1, 0.1])

# Measurement noise covariance (R)
R = np.diag([true_noise_std**2])

# State transition matrix (A)
dt = t[1] - t[0]
A = np.array([[1, dt],
              [0, 1]])

# Measurement matrix (H)
H = np.array([[1, 0]])

# Kalman Filter Loop
estimated_amplitude = []
estimated_frequency = []
for i in range(len(t)):
    # Prediction step
    x_hat_minus = np.dot(A, x_hat)
    P_minus = np.dot(np.dot(A, P), A.T) + Q
    
    # Update step (measurement)
    y = quantized_signal[i] - np.dot(H, x_hat_minus)
    S = np.dot(np.dot(H, P_minus), H.T) + R
    K = np.dot(np.dot(P_minus, H.T), inv(S))
    x_hat = x_hat_minus + np.dot(K, y)
    P = np.dot((np.eye(len(x_hat)) - np.dot(K, H)), P_minus)
    
    estimated_amplitude.append(x_hat[0])
    estimated_frequency.append(x_hat[1])

# MAP Estimation (Posterior Mean)
map_amplitude = np.mean(estimated_amplitude)
map_frequency = np.mean(estimated_frequency)

# Plotting
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(t, true_signal, label='True Signal')
plt.plot(t, noisy_signal, label='Noisy Signal')
plt.title('True and Noisy Signals')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.subplot(3, 1, 2)
plt.plot(t, noisy_signal, label='Noisy Signal')
plt.plot(t, quantized_signal, label='Quantized Signal (8-bit)')
plt.title('Noisy and Quantized Signals')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(t, true_amplitude * np.ones_like(t), 'r--', label='True Amplitude')
plt.plot(t, map_amplitude * np.ones_like(t), 'g--', label='MAP Estimated Amplitude')
plt.plot(t, true_frequency * np.ones_like(t), 'b--', label='True Frequency')
plt.plot(t, map_frequency * np.ones_like(t), 'c--', label='MAP Estimated Frequency')
plt.title('MAP Estimation of Amplitude and Frequency')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()

plt.tight_layout()
plt.show()

import numpy as np
import scipy.stats as stats

# サンプルデータ（正規分布に従う乱数生成）
np.random.seed(0)
data = np.random.normal(loc=0, scale=1, size=100)

# Zスコアに基づく外れ値除去
def remove_outliers_zscore(data, threshold=3):
    z_scores = np.abs((data - np.mean(data)) / np.std(data))
    return data[z_scores < threshold]

# IQRに基づく外れ値除去
def remove_outliers_iqr(data):
    q1, q3 = np.percentile(data, [25, 75])
    iqr = q3 - q1
    lower_bound = q1 - 1.5 * iqr
    upper_bound = q3 + 1.5 * iqr
    return data[(data >= lower_bound) & (data <= upper_bound)]

# 外れ値除去前のデータ長
print("外れ値除去前のデータ長:", len(data))

# Zスコアに基づく外れ値除去
filtered_data_z = remove_outliers_zscore(data)
print("Zスコアに基づく外れ値除去後のデータ長:", len(filtered_data_z))

# IQRに基づく外れ値除去
filtered_data_iqr = remove_outliers_iqr(data)
print("IQRに基づく外れ値除去後のデータ長:", len(filtered_data_iqr))

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Generate sample data (2-dimensional data as an example)
np.random.seed(0)
X = np.random.randn(100, 2)  # 100 samples with 2 features each

# Apply PCA
pca = PCA(n_components=2)  # Extract 2 principal components
pca.fit(X)

# Get principal components
components = pca.components_
explained_variance = pca.explained_variance_ratio_

# Print principal components and explained variance ratio
print("Principal Components:")
print(components)
print("Explained Variance Ratio:")
print(explained_variance)

# Transform data to principal component space
X_transformed = pca.transform(X)

# Visualize
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], alpha=0.8, label='Original Data')
plt.scatter(X_transformed[:, 0], X_transformed[:, 1], alpha=0.8, label='Transformed to Principal Component Space')
plt.title('Data Transformation by PCA')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# データ生成
np.random.seed(0)
n = 100
x1 = np.random.normal(0, 1, size=n)
x2 = 0.5 * x1 + np.random.normal(0, 0.2, size=n)
X = np.vstack((x1, x2)).T

# PCAで次元削減
pca = PCA(n_components=1)
X_pca = pca.fit_transform(X)

# グラフの描画
fig, axs = plt.subplots(1, 2, figsize=(12, 6))

# 元の2次元データの散布図
axs[0].scatter(X[:, 0], X[:, 1])
axs[0].set_title('Original Data')
axs[0].set_xlabel('X1')
axs[0].set_ylabel('X2')

# PCAによる1次元データの散布図
axs[1].scatter(X_pca, np.zeros_like(X_pca), alpha=0.5)
axs[1].set_title('PCA Dimensionality Reduction')
axs[1].set_xlabel('Principal Component 1')
axs[1].set_yticks([])

plt.tight_layout()
plt.show()

import numpy as np

def gaussian_kernel_matrix(X, sigma=1.0):
    """
    Computes the Gaussian kernel matrix K using matrix-matrix multiplication for efficiency.

    Parameters:
    X : numpy.ndarray
        Input data matrix of shape (n, m).
    sigma : float, optional
        Kernel parameter (default is 1.0).

    Returns:
    K : numpy.ndarray
        Gaussian kernel matrix of shape (n, n).
    """
    n = X.shape[0]
    G = np.sum(X**2, axis=1)  # Compute vector g
    K = np.exp(-(G.reshape(-1, 1) + G - 2 * np.dot(X, X.T)) / (2 * sigma**2))
    return K

def efficient_S_matrix(X, W):
    """
    Computes the matrix S efficiently using matrix-matrix multiplication.

    Parameters:
    X : numpy.ndarray
        Input data matrix of shape (n, m).
    W : numpy.ndarray
        Weight matrix of shape (n, n).

    Returns:
    S : numpy.ndarray
        Matrix S computed using efficient method.
    """
    n, m = X.shape
    S = 2 * np.dot(X.T, (np.diag(np.sum(W, axis=1)) - W).dot(X))
    return S

# Example usage
n = 100  # Number of samples
m = 2  # Dimension of each sample
X = np.random.randn(n, m)  # Sample data matrix
W = np.random.randn(n, n)  # Weight matrix
sigma = 1.0  # Kernel parameter

# Compute Gaussian kernel matrix
K = gaussian_kernel_matrix(X, sigma)
print("Gaussian Kernel Matrix K:")
print(K)

# Compute matrix S efficiently
S = efficient_S_matrix(X, W)
print("\nMatrix S computed efficiently:")
print(S)